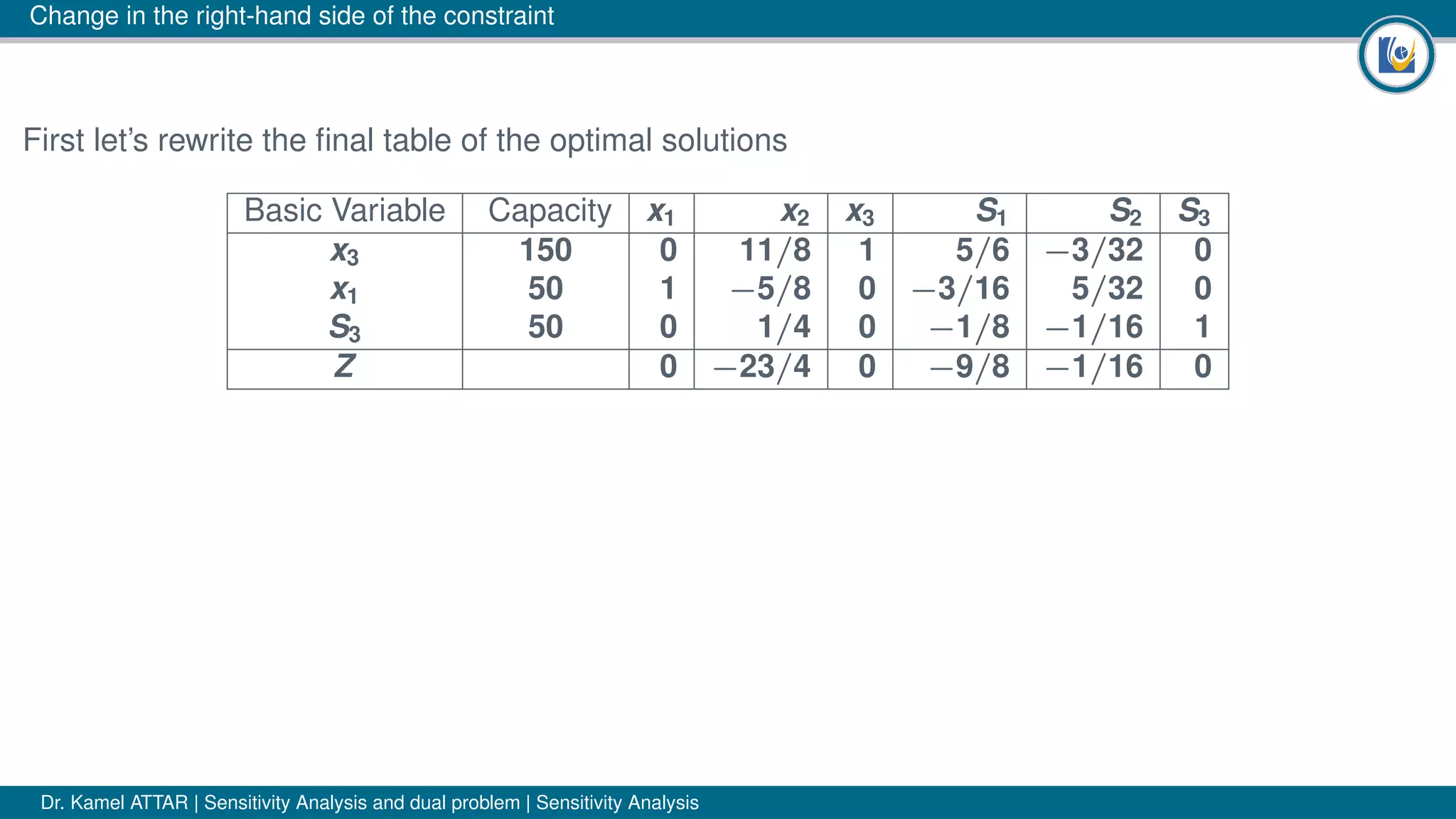
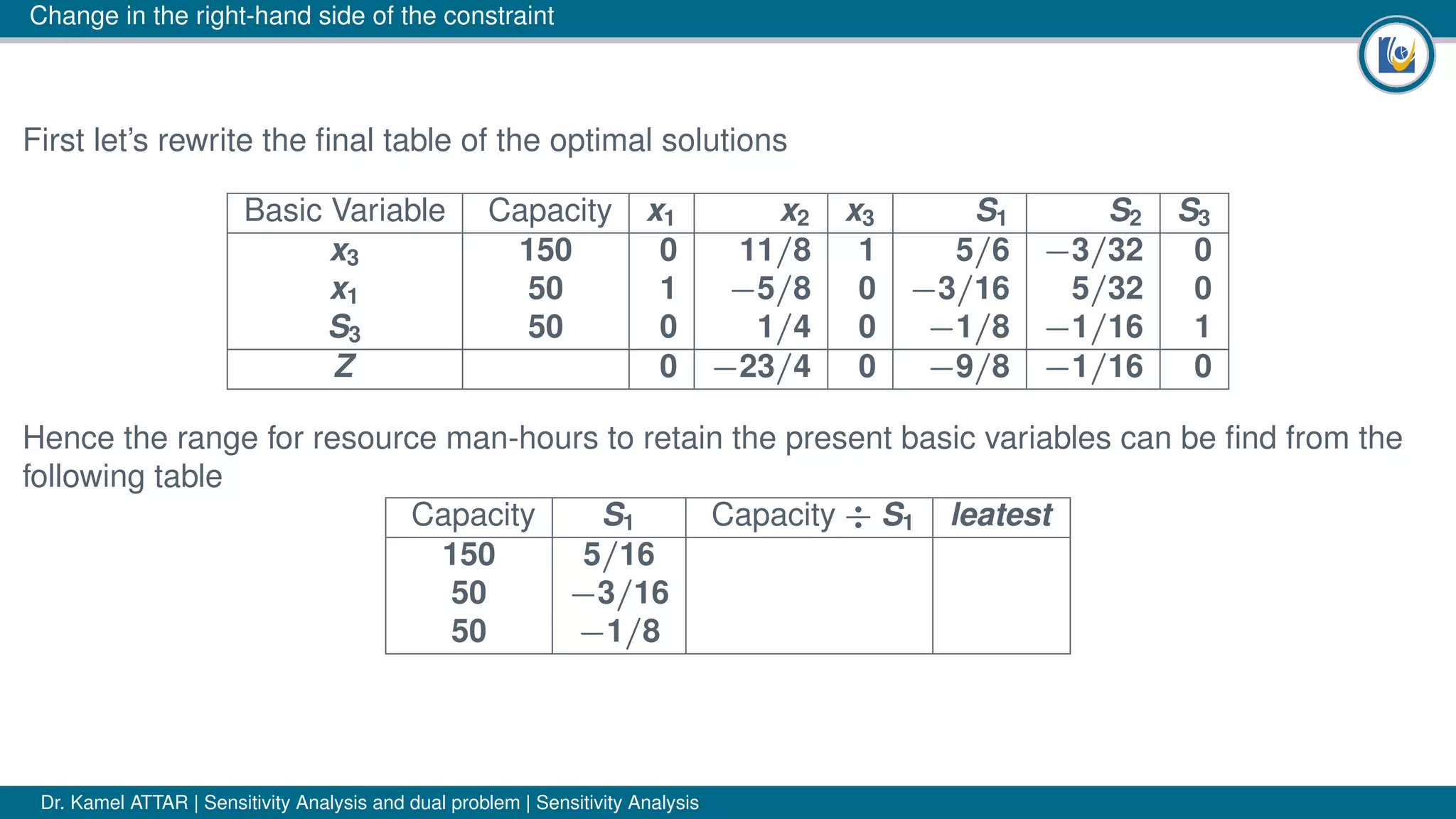
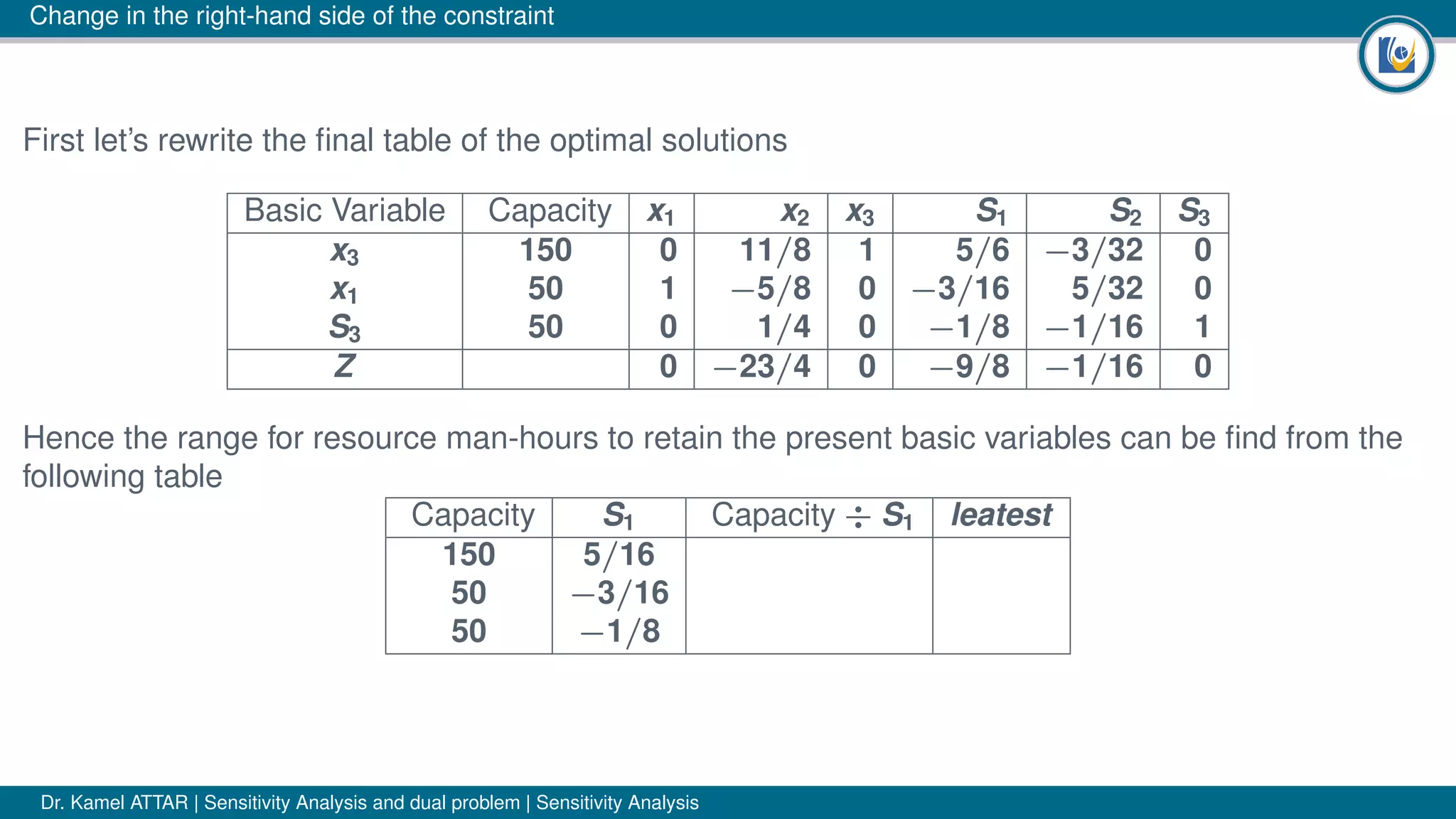
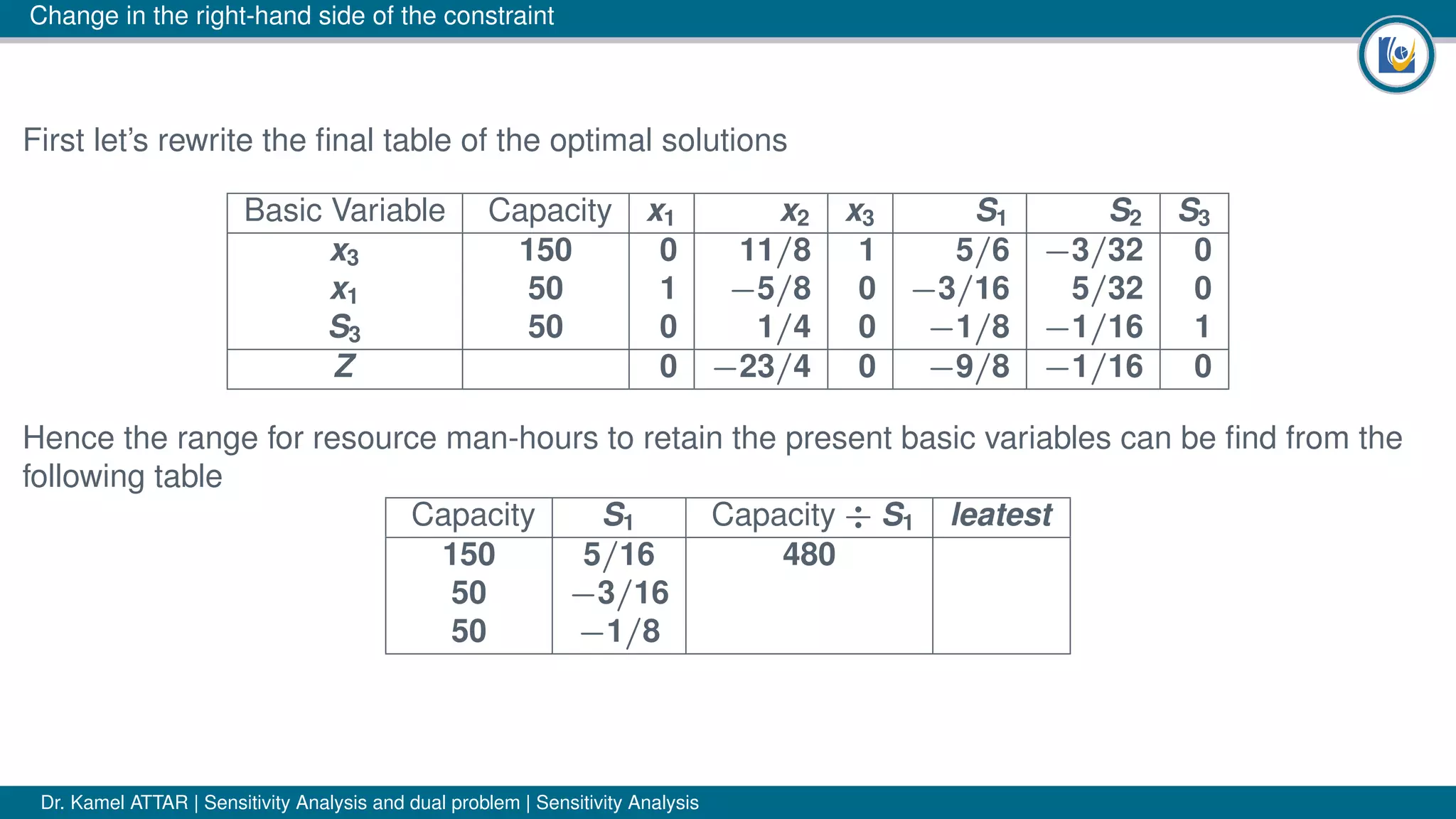
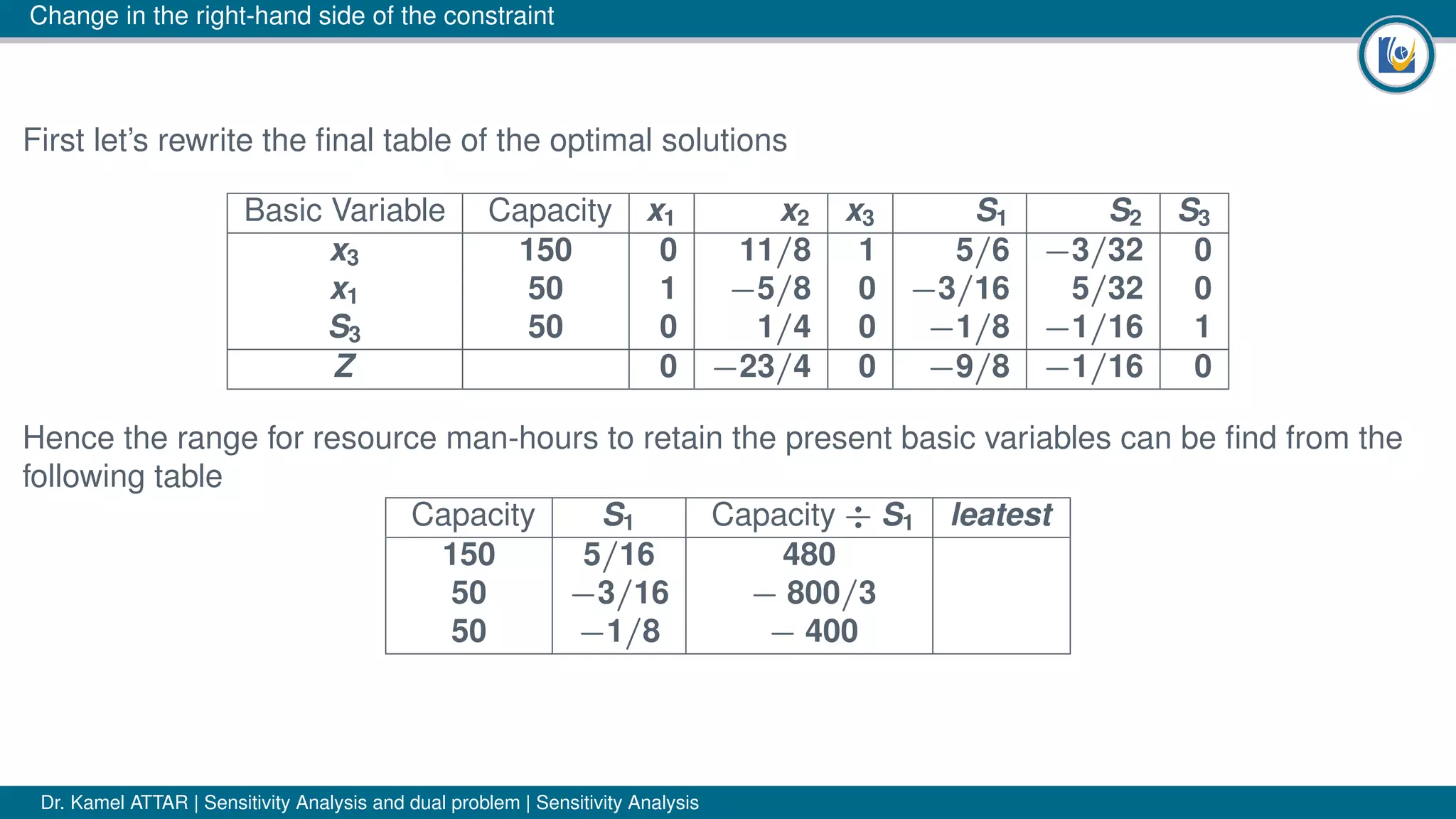
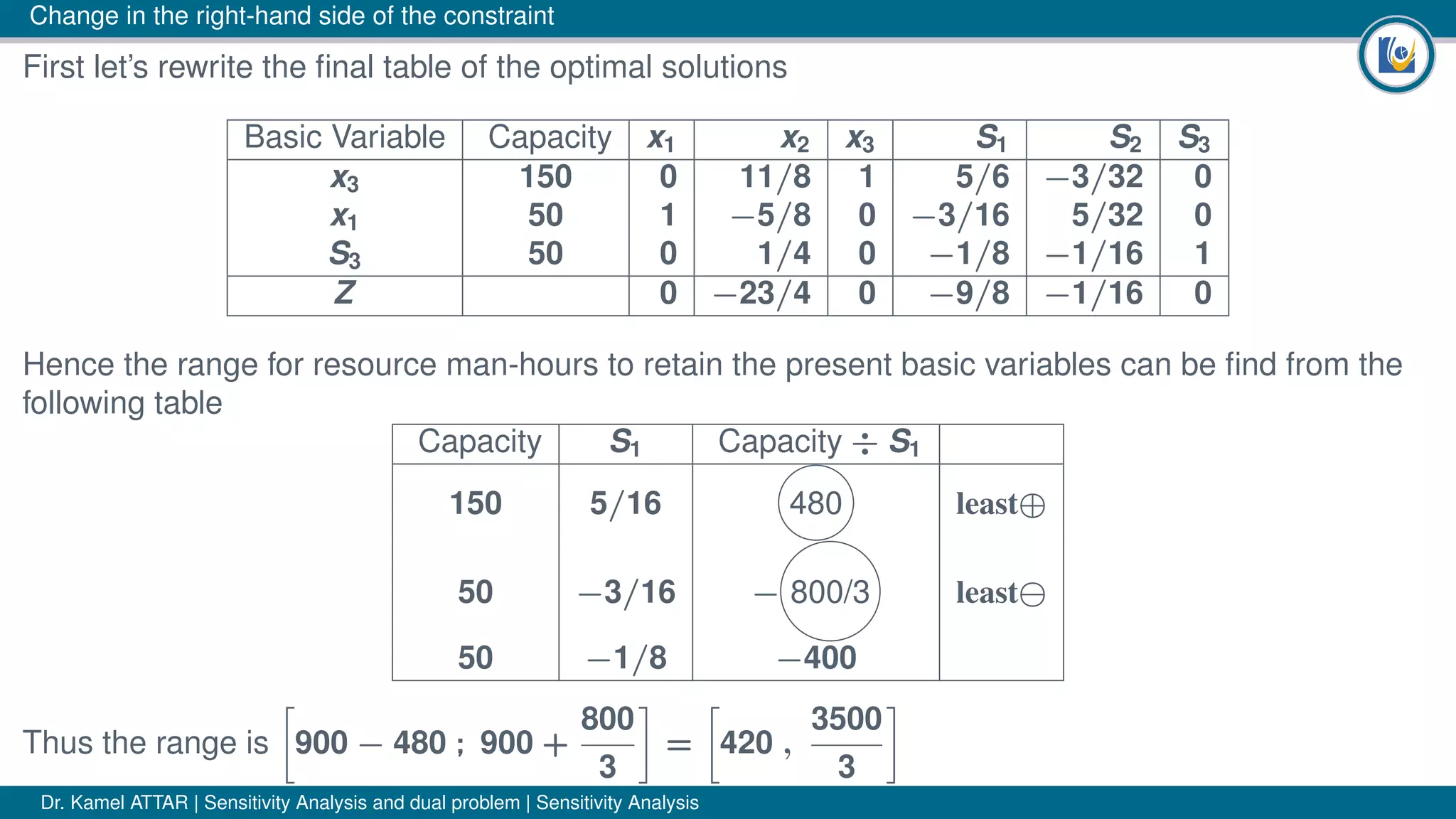
The document discusses sensitivity analysis in linear programming, focusing on how changes in coefficients or resource availability impact optimal solutions. It emphasizes the necessity for managers to understand these sensitivities in dynamic conditions, outlining three possible cases of change: no change, same variables with altered values, and complete solution change. The author illustrates concepts using examples, including the significance of shadow prices for resource allocation decisions.