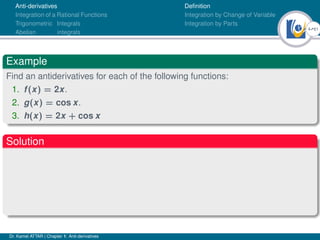
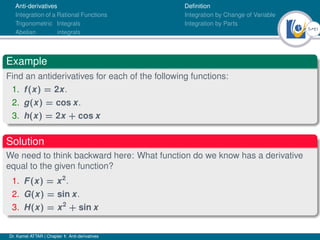
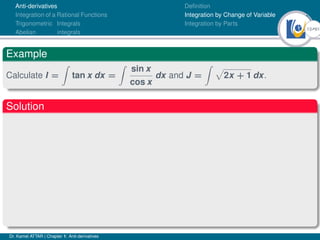
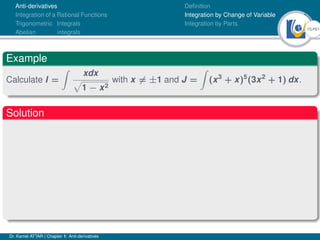
This document outlines a lecture on anti-derivatives given by Dr. Kamel ATTAR. The lecture covers various topics related to anti-derivatives including definitions, indefinite integrals, integration by substitution, integration by parts, and examples of evaluating definite and indefinite integrals of various functions. Dr. ATTAR provides examples and exercises for students to practice evaluating integrals using the techniques covered in the lecture.








![11Ú61
Anti-derivatives
Integration of a Rational Functions
Trigonometric Integrals
Abelian integrals
Definition
Integration by Change of Variable
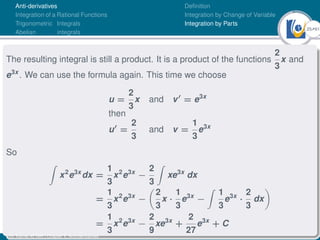
Integration by Parts
Integration by Change of Variable
Theorem
If ϕ : [α, β] → R is a continuously differentiable function and if f is continuous
mapping on an interval contained ϕ
[α, β]
, then :
Z
f
ϕ(x)
ϕ0
(x) dx =
Z
f(t) dt
We can say that we perform the change of variable t = ϕ(x).
Dr. Kamel ATTAR | Chapter 1: Anti-derivatives](https://image.slidesharecdn.com/simpleintegral-210413091739/85/Simple-integral-11-320.jpg)

































![48Ú61
Anti-derivatives
Integration of a Rational Functions
Trigonometric Integrals
Abelian integrals
Products of Powers of Sines and Cosines
Products of Sines and Cosines
Bioche Rule
Products of Sines and Cosines
Z
sin mx sin nx dx ,
Z
sin mx cos nx dx and
Z
cos mx cos nx dx .
We use the simpler identities:
¶ sin mx sin nx =
1
2
[cos(m − n)x − cos(m + n)x]
· sin mx cos nx =
1
2
[sin(m − n)x + sin(m + n)x]
¸ cos mx cos nx =
1
2
[cos(m − n)x + cos(m + n)x]
Example
Z
cos(5x) sin(3x) dx =
Z
sin(8x) − sin(2x)
2
dx = cos(2x)/4 − cos(8x)/16 + C .
Dr. Kamel ATTAR | Chapter 1: Anti-derivatives](https://image.slidesharecdn.com/simpleintegral-210413091739/85/Simple-integral-48-320.jpg)












