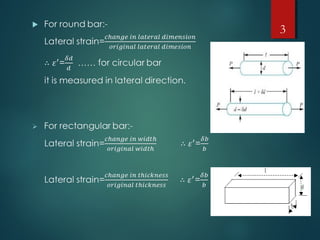
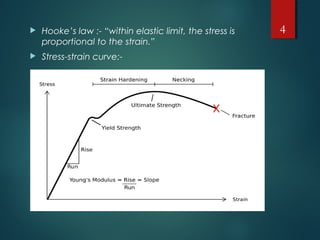
This document discusses elastic constants in isotropic materials. It defines four elastic constants: modulus of elasticity (E), Poisson's ratio (ν), shear modulus (G), and bulk modulus (K). It provides formulas for the relationships between these constants, specifically that K=E/3(1-2ν) and G=E/2(1+ν). An example problem is shown to calculate E and ν for a prismatic specimen under uniaxial loading. Various elastic properties of common materials like metals and composites are also listed.

1. ELASTIC CONSTANTS IN
ISOTROPIC MATERIALS
1.Elasticity Modulus (E)
2. Poisson’s Ratio (ν)
3. Shear Modulus (G)
4. Bulk Modulus (K)
1

2. 1. Modulus of Elasticity, E
(Young’s Modulus)
2

3. 3

4. 4 Hooke’s law :- “within elastic limit, the stress is
proportional to the strain.”
 Stress-strain curve:-

5. 5

7. Shear Modulus, G 7

8. Bulk modulus(K)

9. Example:
Uniaxial Loading of a Prismatic Specimen
AfterBefore
10 cm
10 cm
10 cm
10.4 cm
9.9 cm
9.9 cm
Determine
E and ν
P=1000 kgf
9

10. 10cm
10cm
Δl/2=0.2cm
Δd/2=0.05cm
1000 kgf
P=1000 kgf
P=1000kgf → σ=
10*10
1000
= 10kgf/cm2
E=
σ
ε =
10
0.04
= 250 kgf/cm2
εlong=
Δl
l0
= =0.04
0.4
10
εlat=
Δd
d0
= = -0.01
-0.1
10
ν = -
-0.01
0.04
= 0.25
10

11. RELATION B/W K & E
 Consider a cube with a unit volume
σ
1
1
1
σ
D
C
BA
σ causes an elongation in the direction
CD and contraction in the directions AB
& BC.
The new dimensions of the cube is :
• CD direction is 1+ε
• BC direction is 1-νε
• AB direction is 1-νε
11

12.  V0 = 1
 Final volume Vf of the cube is now:
(1+ε) (1-νε) (1-νε) = (1+ε) (1-2νε+μ2
ε2
)
= 1 - 2νε + μ2
ε2
+ ε-2νε2
+ μ2
ε3
= 1 + ε - 2νε - 2νε2
+ μ2
ε2
+ μ2
ε3
ε is small, ε2
& ε3
are smaller and can be neglected.
 Vf = 1+ ε - 2νε → ΔV = Vf - V0 = ε (1-2ν)
 If equal tensile stresses are applied to each
of the other two pairs of faces of the cube than
the total change in volume will be :
ΔV = 3ε (1-2ν)
12

13. σ
σ
σ
σ
σ
σ
Ξ + +
K =
(σ+σ+σ)/3 σ
=
3ε (1-2ν)
=
3ε (1-2ν)
E
3 (1-2ν)
K =
E
3 (1-2ν)
ΣΔV = 3ε (1-2ν) = ε (1-2ν) ε (1-2ν) ε (1-2ν)+ +
=
σavg
∆V/V0
13

14.  Moreover the relation between G
and E is :
G =
E
2 (1+ν)
 The relation betweenThe relation between
G, E and K is :G, E and K is :
E
1 1
=
1
+
9K 3G
K =
E
3 (1-2ν)
 The relation betweenThe relation between
K and E is :K and E is :
Therefore, out of the four elastic constants
only two of them are independent.
14

15.  For very soft materials such as pastes, gels,For very soft materials such as pastes, gels,
putties, K is very largeputties, K is very large
 Note that as KNote that as K → ∞ →→ ∞ → νν →→ 0.5 & E ≈ 3G0.5 & E ≈ 3G
If K is very large →If K is very large → ΔΔV/VV/V00 ≈ 0≈ 0 **No volumeNo volume
changechange
 For materials like metals, fibers & certainFor materials like metals, fibers & certain
plastics K must be considered.plastics K must be considered.
15

16.  Modulus of Elasticity :
• High in covalent compounds such as diamond
• Lower in metallic and ionic crystals
• Lowest in molecular amorphous solids such as plastics and rubber.
16

17. Elastic Constants of Some
MaterialsE(psi)x10E(psi)x1066
(GPa)(GPa)
G(psi)x10G(psi)x1066
(GPa)(GPa)
νν (-)(-)
Cast IronCast Iron 1616 110110 7.47.4 5050 0.170.17
SteelSteel 3030 205205 11.811.8 8080 0.260.26
AluminumAluminum 1010 7070 3.63.6 2525 0.330.33
ConcreteConcrete 1.5-5.51.5-5.5 10-4010-40 0.62-2.300.62-2.30 4-154-15 0.20.2
WoodWood Long 1.81Long 1.81 1212
Tang 0.10Tang 0.10 0.70.7
0.110.11 0.70.7
0.030.03 0.20.2
??
17

18. Thank You
18