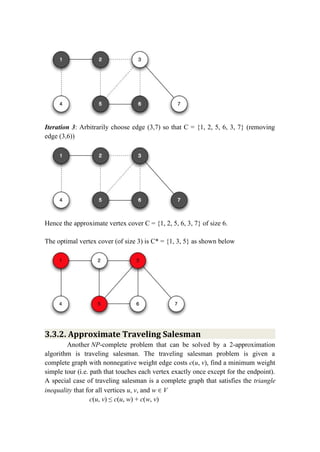
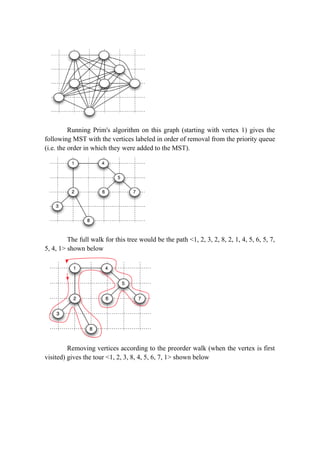
The document discusses approximation algorithms for NP-complete problems. It introduces the concept of approximation ratios, which measure how close an approximate solution from a polynomial-time algorithm is to the optimal solution. The document then provides examples of approximation algorithms with a ratio of 2 for the vertex cover and traveling salesman problems. It also discusses using backtracking to find all possible solutions to the subset sum problem.

1. Approximation Algorithms
Many problems of practical significance are NP-complete but are
too important to abandon nearly because obtaining an optimal solution is
intractable. If a problem is NP-complete it is unlikely to find a polynomial time
algorithm for solving it exactly.
There are 3 approaches to getting around NP-completeness:
I. If the actual inputs are small an algorithm with exponential
running time may be perfectly satisfactory.
II. We may be able to isolate important special cases that are solvable
in polynomial time.
III. It may be possible to find near optimal solutions in polynomial time either
in the worst case or an average.
An algorithm that returns near optimal solution is called an approximation
algorithm.
Performance ratio for approximation algorithms:
Suppose we are working on an optimization problem in which
each potential solution has a positive cost and we wish to find a near optimal
solution. Depending on the problem an optimal solution may be defined as one
with minimum possible cost. That is a problem may be either a minimization or
maximization problem.
While there is no efficient way of finding the optimal solution to several of
them, e.g. traveling salesman, there are ways to efficiently find approximate
solutions. It is interesting that while we may not know the optimal value, we can
know how far (worst case) our approximate solution is from the optimal.
Performance Ratio
We define a quantity ρ(n) known as the approximation ratio as
This ratio measures the ratio between the approximate solution and the
optimal solution. Clearly the optimal solution has ρ(n) = 1. Thus if we can show a
particular performance ratio for an approximation algorithm, we can say that the

2. approximate solution is within a factor of ρ(n) of the optimal (again without
knowing what the optimal value is). Such a solution is known as a ρ(n)-
approximation algorithm.
3.3.1. Approximate Vertex Cover
The first problem we will find an approximate solution to is vertex cover.
As a review, the vertex cover problem is to find the minimum subset of vertices that
touch every edge in a graph.
The following algorithm can find an approximate vertex cover that contains
no more than twice the minimum number of vertices, i.e. is a 2-approximation
algorithm.
Algorithm
APPROX-VERTEX-COVER(G)
1. C = ∅
2. E' = G.E
3. while E' ≠ ∅
4. let (u,v) be an arbitrary edge of E'
5. C = C ∪ {u,v}
6. remove from E' every edge incident on either u or v
7. return C
The algorithm simply selects an edge (adding the endpoints to the vertex
cover) and removes any other edges incident on its endpoints (since these are
covered by the endpoints). It repeats this process until there are no more edges to
remove. Clearly this algorithm runs in polynomial time (O(E)).
Proof
Clearly when the algorithm terminates, the set C will be a vertex cover (since all
edges will be touched by a vertex). Assume line 4 of the algorithm keeps the set of
edges A. To cover these edges, any vertex cover (including the optimal one C*)
needs to contain at least one endpoint for each edge. However in A, no two edges
share an endpoint since once an edge is selected in line 4, all other edges incident to
its endpoints are removed. Therefore, no two edges in A are covered by the same
vertex from C* giving
|C*| ≥ |A|

3. Because the algorithm selects edges with endpoints not currently in the set C,
clearly (since every edge will have 2 distinct vertices)
|C| = 2 |A|
Combining these two equations gives
|C*| ≥ |C| / 2
⇒ |C| ≤ 2 |C*|
Hence the algorithm returns a vertex cover with no more than twice the number of
vertices in an optimal vertex cover.
Example
Consider the following graph
Iteration 1: Arbitrarily choose edge (1,2) so that C = {1, 2} (removing edges (1,4),
(2,3) and (2,5))
Iteration 2: Arbitrarily choose edge (5,6) so that C = {1, 2, 5, 6} (removing edges
(2,5) and (3,5))

4. Iteration 3: Arbitrarily choose edge (3,7) so that C = {1, 2, 5, 6, 3, 7} (removing
edge (3,6))
Hence the approximate vertex cover C = {1, 2, 5, 6, 3, 7} of size 6.
The optimal vertex cover (of size 3) is C* = {1, 3, 5} as shown below
3.3.2. Approximate Traveling Salesman
Another NP-complete problem that can be solved by a 2-approximation
algorithm is traveling salesman. The traveling salesman problem is given a
complete graph with nonnegative weight edge costs c(u, v), find a minimum weight
simple tour (i.e. path that touches each vertex exactly once except for the endpoint).
A special case of traveling salesman is a complete graph that satisfies the triangle
inequality that for all vertices u, v, and w ∈ V
c(u, v) ≤ c(u, w) + c(w, v)

5. basically that it is faster to go directly between two points than through an
intermediate vertex. It can be shown that even by imposing this constraint on the
graph that this version of traveling salesman is still NP-complete (and also that
without this constraint that there is no good approximation algorithm
unless P = NP).
The following algorithm, which utilizes Prim's algorithm for finding MST,
can find a tour of weight no more than twice the optimal.
A preorder tree walk simply recursively visits vertices in the tree based on when
they were discovered. This approximation algorithm runs in O(V2).
Proof
Let H* be an optimal tour with cost c(H*). Since we can construct a
spanning tree from a tour by simply removing any edge (which for TSP is
nonnegative), the cost of the MST T must be a lower bound on the cost of the
optimal tour
c(T) ≤ c(H*)
Consider a full walk W that visits each vertex both upon the initial
recursion and whenever the tour revisits the vertex as recursive branches are
completed. Therefore each edge of T will be traversed exactly twice for W giving
c(W) = 2 c(T)
Combining the above two equations gives
c(W) ≤ 2 c(H*)
However since the walk W visits some vertices more than once, it is not a
tour. But since the graph satisfies the triangle inequality, removing any vertex from
the walk will not increase the cost of the walk (since it will be lower cost to go
direct). By repeatedly removing all but the first visit to each vertex, we obtain the
preordered walk (that contains all the vertices once except for the root) giving a
hamiltonian tour H. Since we only removed vertices from W (not increasing the
cost at any step by the triangle inequality)
c(H) ≤ c(W)
Finally combining this inequality with the previous one gives
c(H) ≤ 2 c(H*)
Thus the tour found by the algorithm will have cost at worst twice the optimal
value.
Example
Consider the following (complete) graph where the edge weights are simply
the Euclidean distances between the vertices (which clearly satisfies the triangle
inequality)

6. Running Prim's algorithm on this graph (starting with vertex 1) gives the
following MST with the vertices labeled in order of removal from the priority queue
(i.e. the order in which they were added to the MST).
The full walk for this tree would be the path <1, 2, 3, 2, 8, 2, 1, 4, 5, 6, 5, 7,
5, 4, 1> shown below
Removing vertices according to the preorder walk (when the vertex is first
visited) gives the tour <1, 2, 3, 8, 4, 5, 6, 7, 1> shown below

7. The optimal tour is shown below in red. The approximate tour has cost ≈ 19.1
whereas the optimal tour has cost ≈ 14.7.
3.3.4. Subset Sum Problem
The subset-sum problem finds a subset of a given set A = {a1, . . . , an}
of n positive integers whose sum is equal to a given positive integer d. For
example, for A = {1, 2, 5, 6, 8} and d = 9, there are two solutions: {1, 2, 6} and
{1, 8}. Of course, some instances of this problem may have no solutions.
It is convenient to sort the set’s elements in increasing order. So, we
will assume that a1< a2 < . . . < an.
A = {3, 5, 6, 7} and d = 15 of the subset-sum problem. The number
inside a node is the sum of the elements already included in the subsets
represented by the node. The inequality below a leaf indicates the reason for its
termination.

8. Complete state-space tree of the backtracking algorithm applied to the
instance
Example:
 The state-space tree can be constructed as a binary tree like that in Figure
for the instance A = {3, 5, 6, 7} and d = 15.
 The root of the tree represents the starting point, with no decisions about
the given elements made as yet.
 Its left and right children represent, respectively, inclusion and exclusion of
a1 in a set being sought. Similarly, going to the left from a node of the first
level corresponds to inclusion of a2 while going to the right corresponds to
its exclusion, and so on.
 Thus, a path from the root to a node on the ith level of the tree indicates
which of the first I numbers have been included in the subsets represented
by that node.
 We record the value of s, the sum of these numbers, in the node.
 If s is equal to d, we have a solution to the problem. We can either report
this result and stop or, if all the solutions need to be found, continue by
backtracking to the node’s parent.
General Remarks
From a more general perspective, most backtracking algorithms fit the
following escription. An output of a backtracking algorithm can be thought of
as an n-tuple (x1, x2, . . . , xn) where each coordinate xi is an element of some

9. finite lin early ordered set Si . For example, for the n-queens problem, each Si
is the set of integers (column numbers) 1 through n.
A backtracking algorithm generates, explicitly or implicitly, a state-
space tree; its nodes represent partially constructed tuples with the first i
coordinates defined by the earlier actions of the algorithm. If such a tuple (x1,
x2, . . . , xi) is not a solution, the algorithm finds the next element in Si+1 that is
consistent with the values of ((x1, x2, . . . , xi) and the problem’s constraints, and
adds it to the tuple as its (i + 1)st coordinate. If such an element does not exist,
the algorithm backtracks to consider the next value of xi, and so on.
Algorithm backtrack(x [1..i] )
//Gives a template of a generic backtracking algorithm
//Input: X[1..i] specifies first i promising components of a solution
//Output: All the tuples representing the problem’s solutions
if X[1..i] is a solution write∈X[1..i]
else //see Problem this section
for each element x Si+1 consistent with X[1..i] and
the constraints do X[i + 1] ← x
Backtrack(X[1..i + 1])