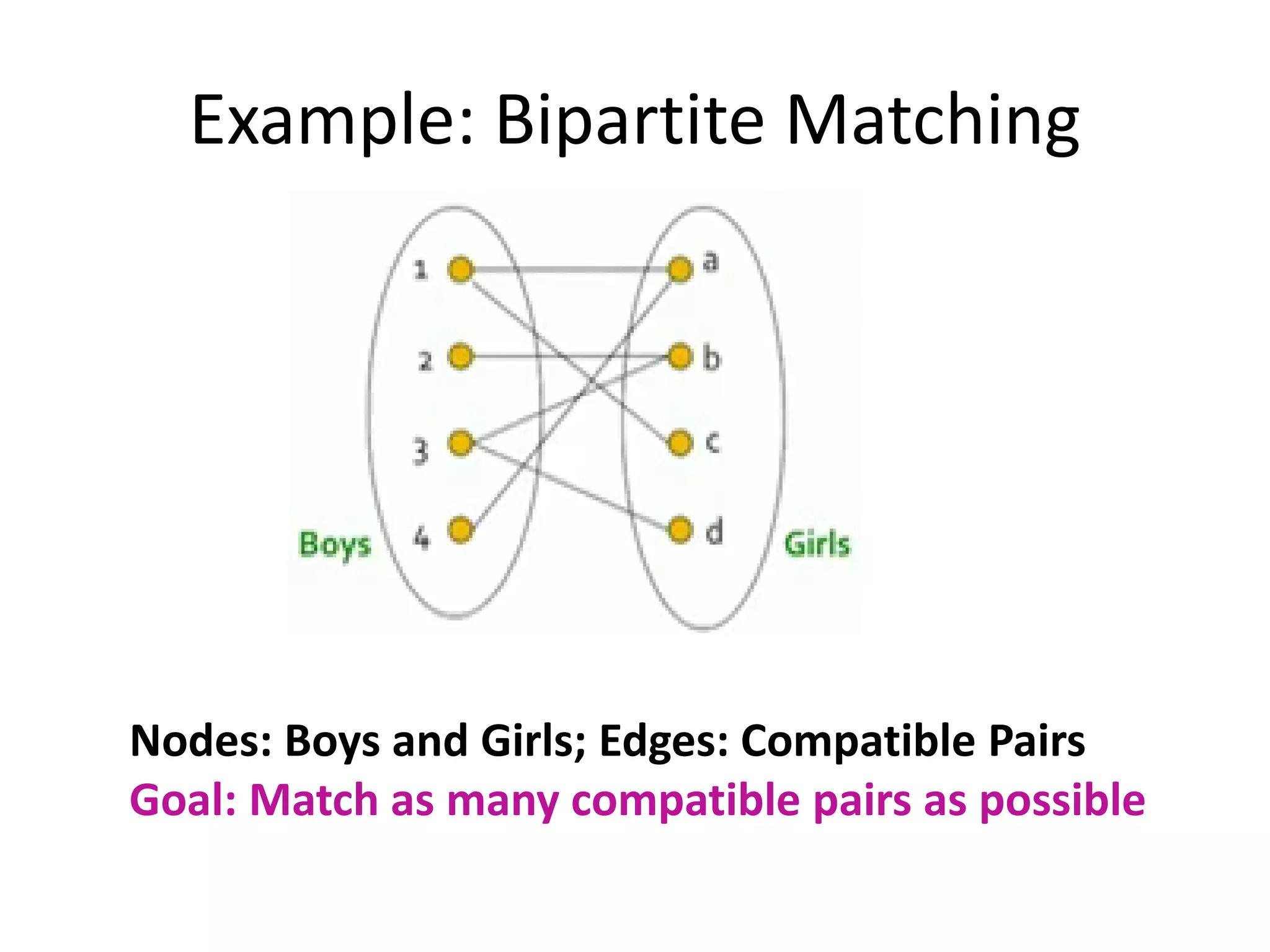
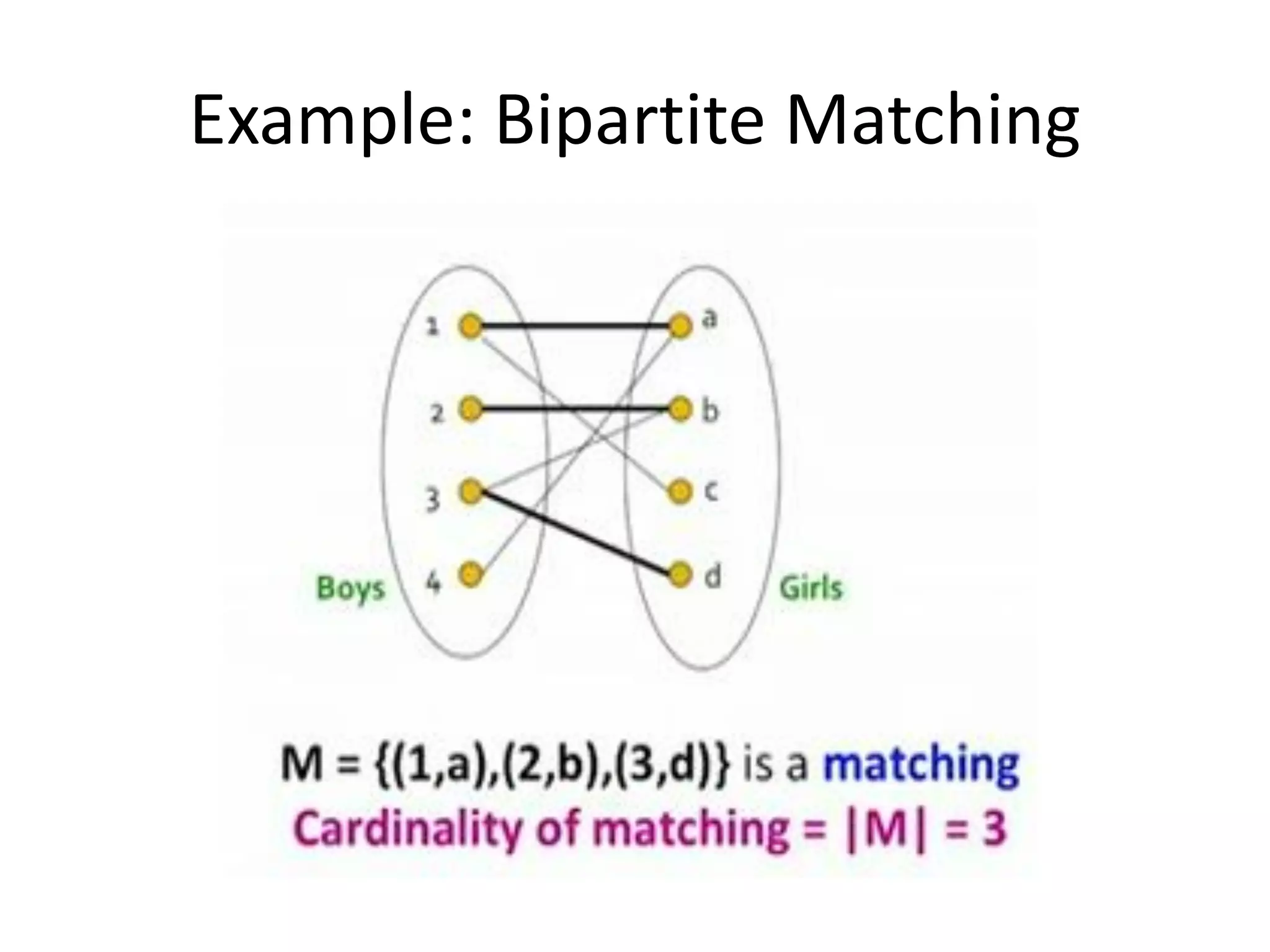
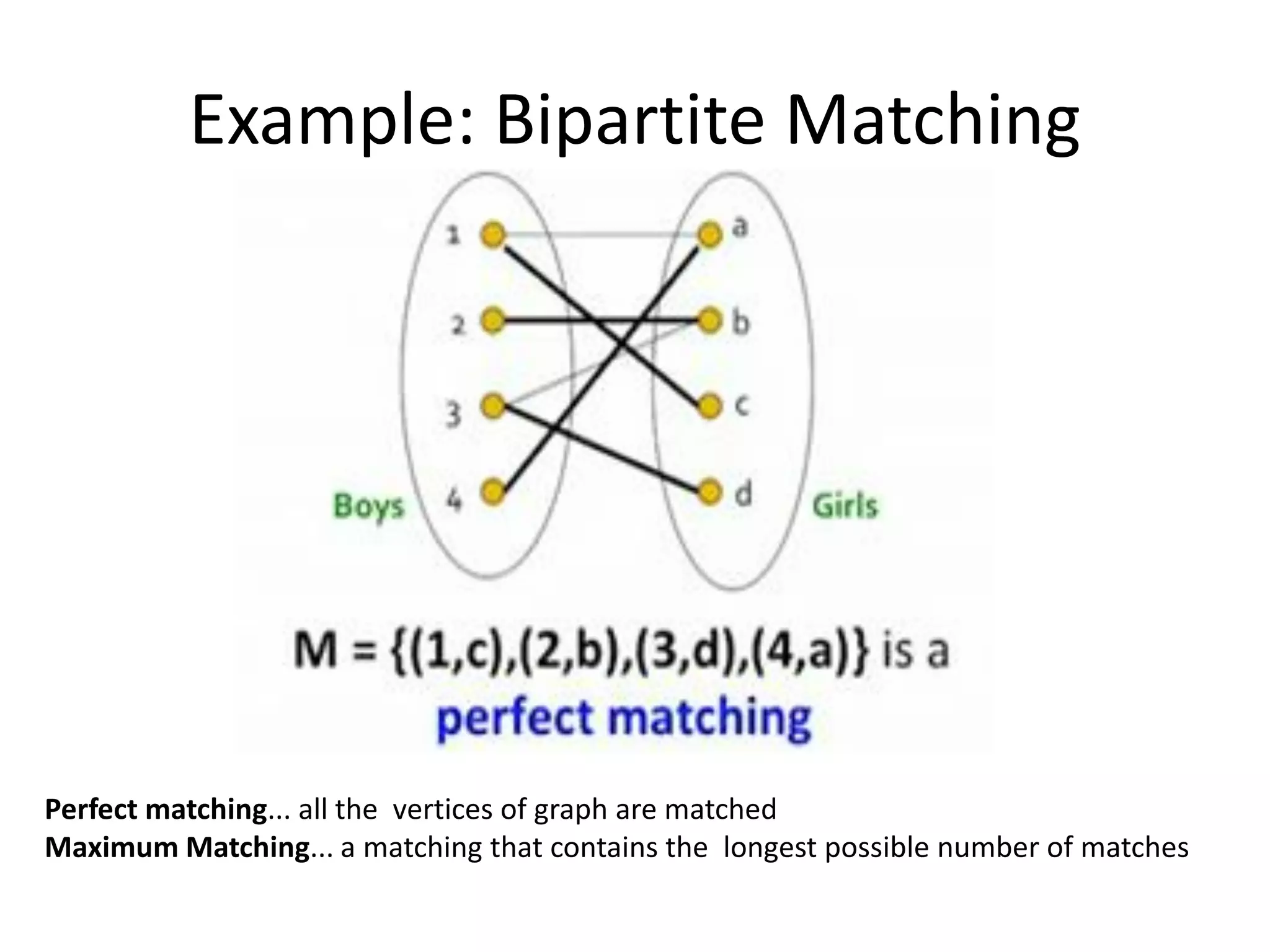
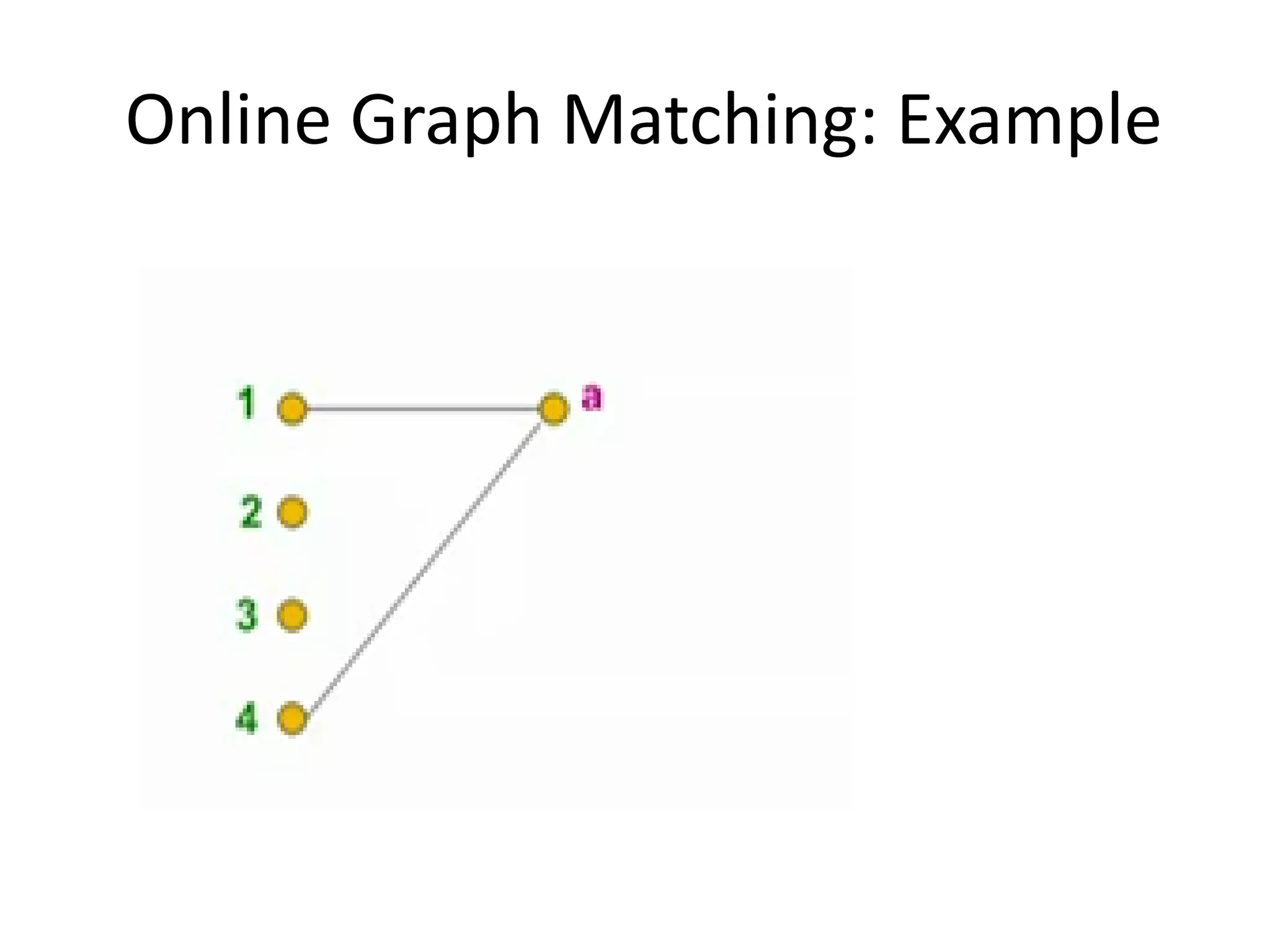
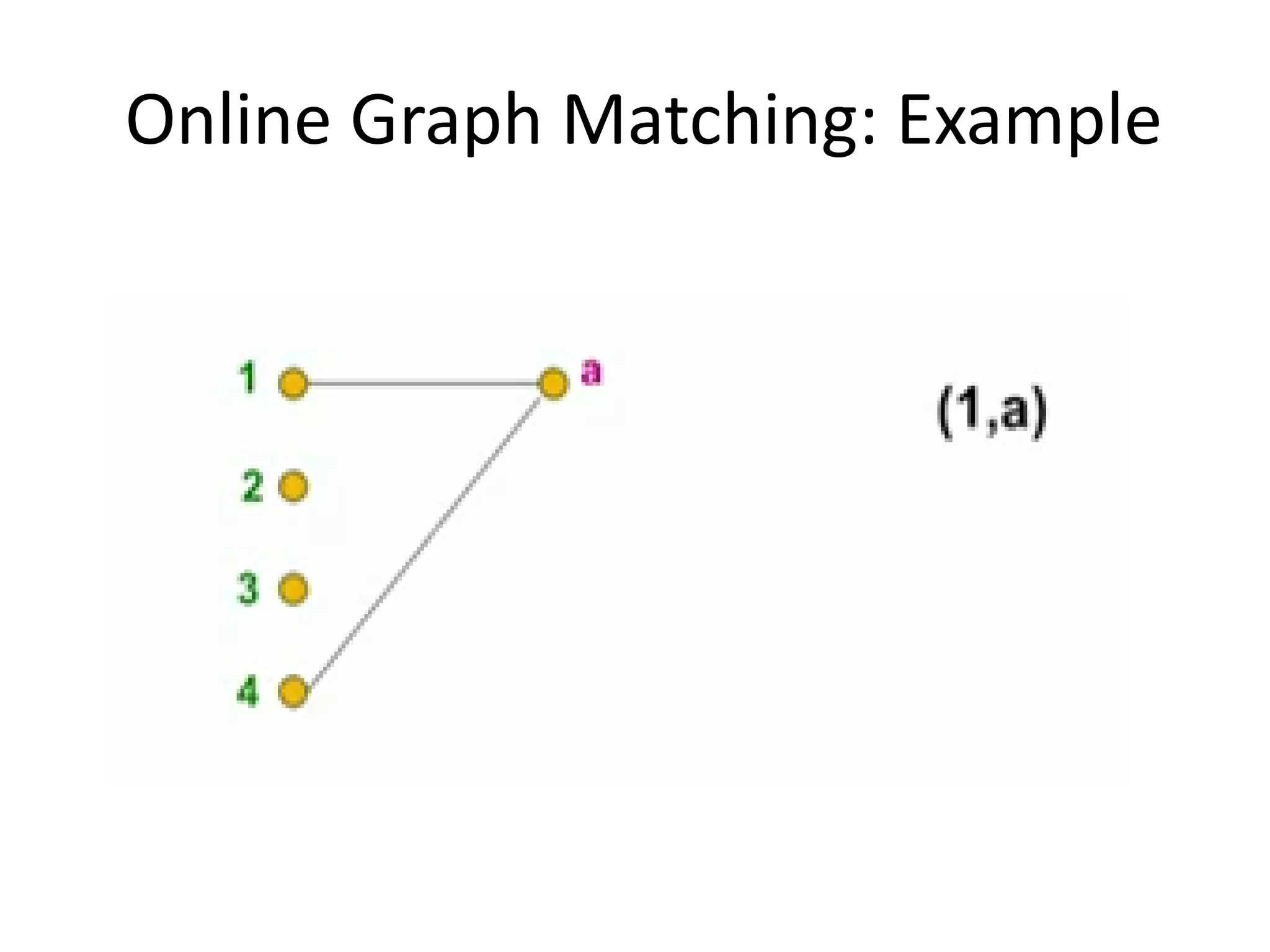
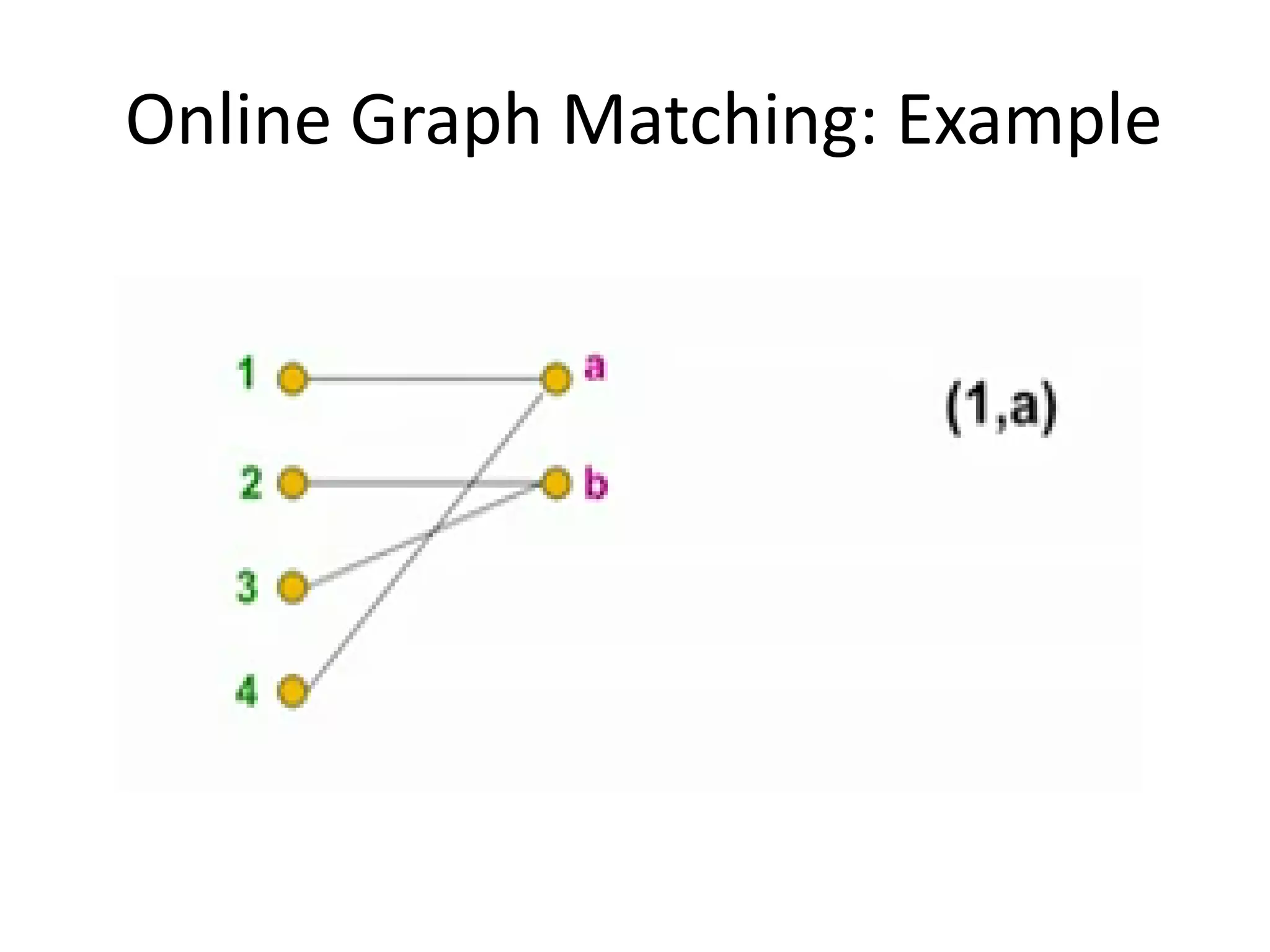
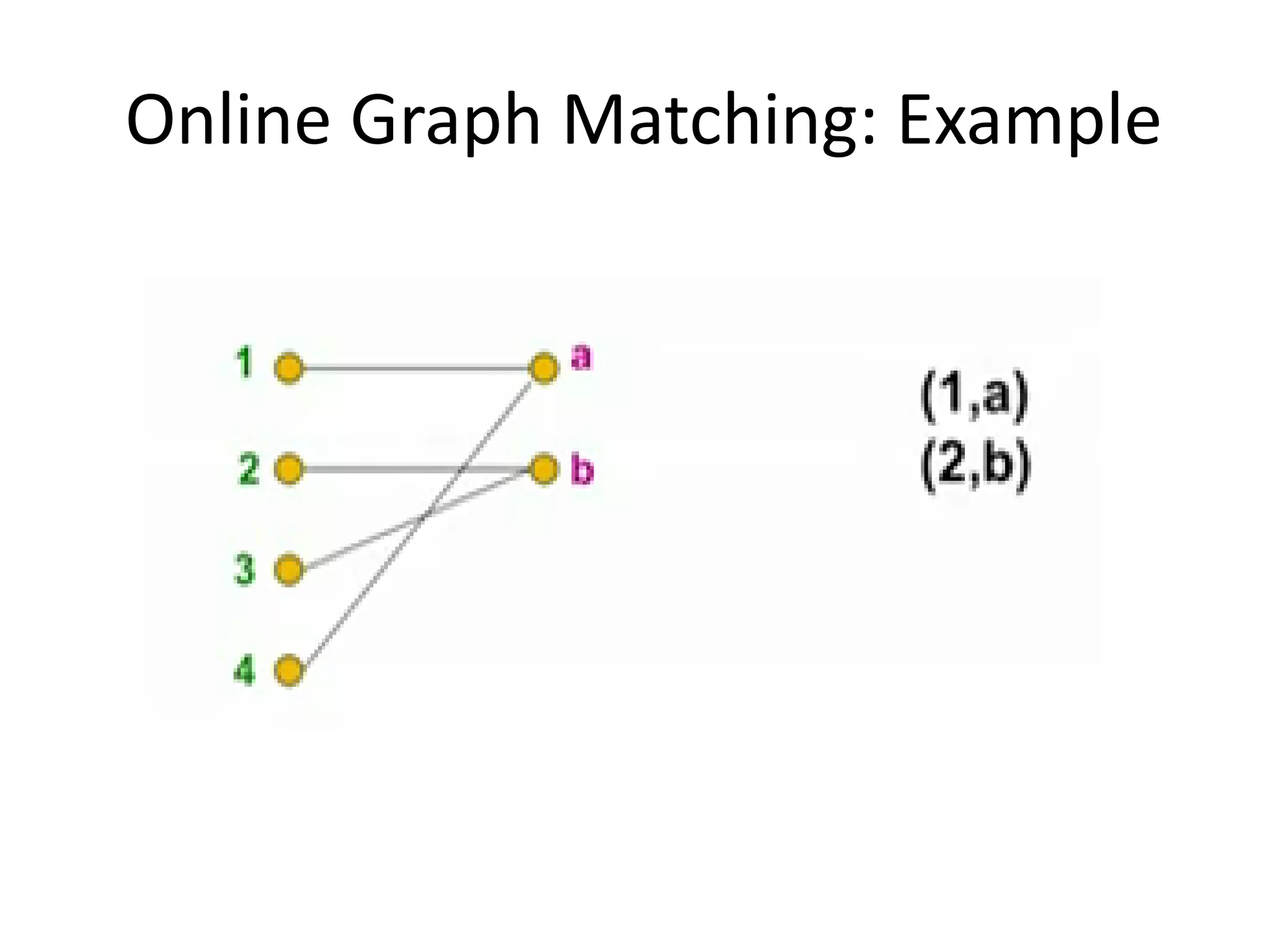
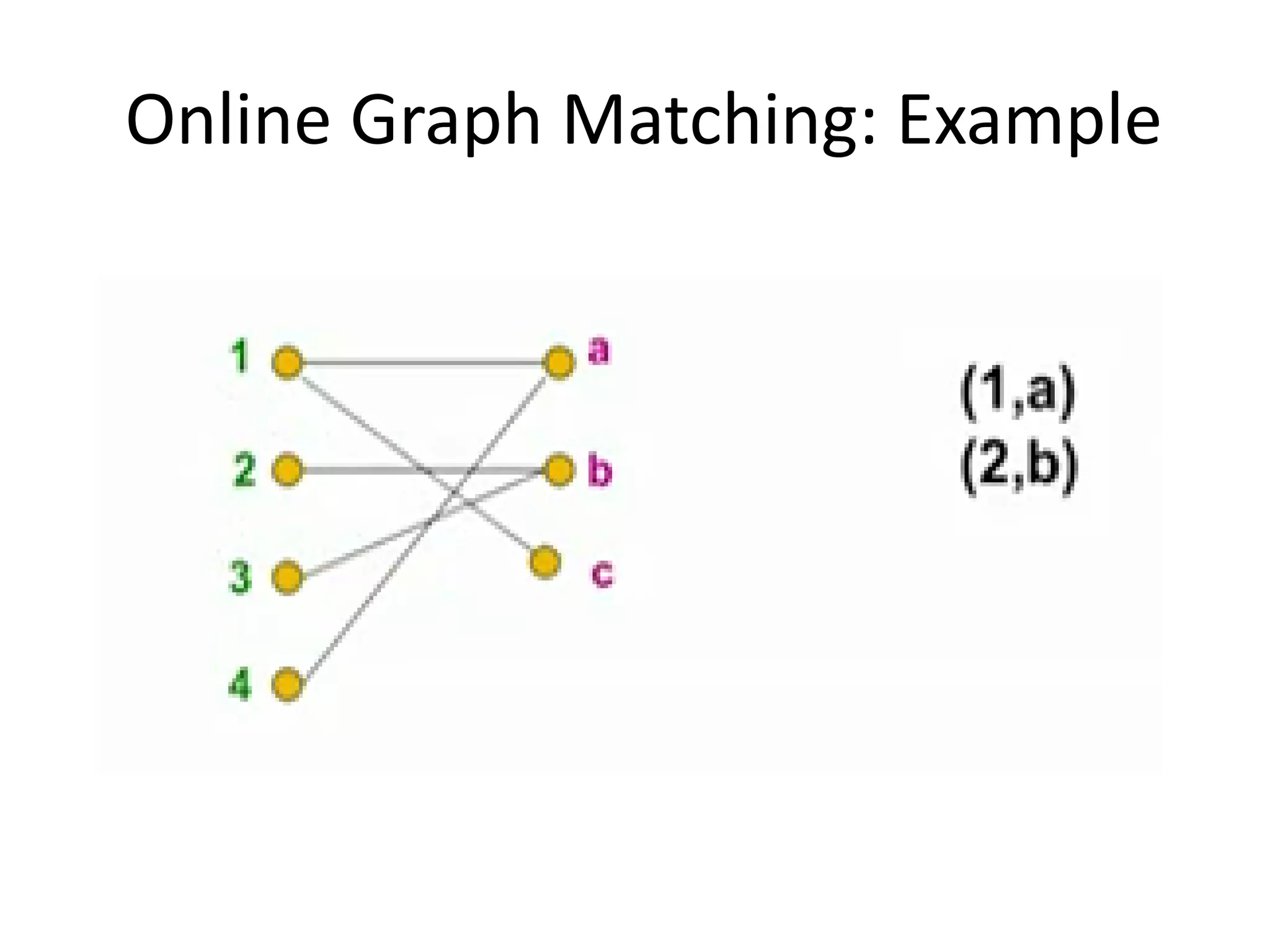
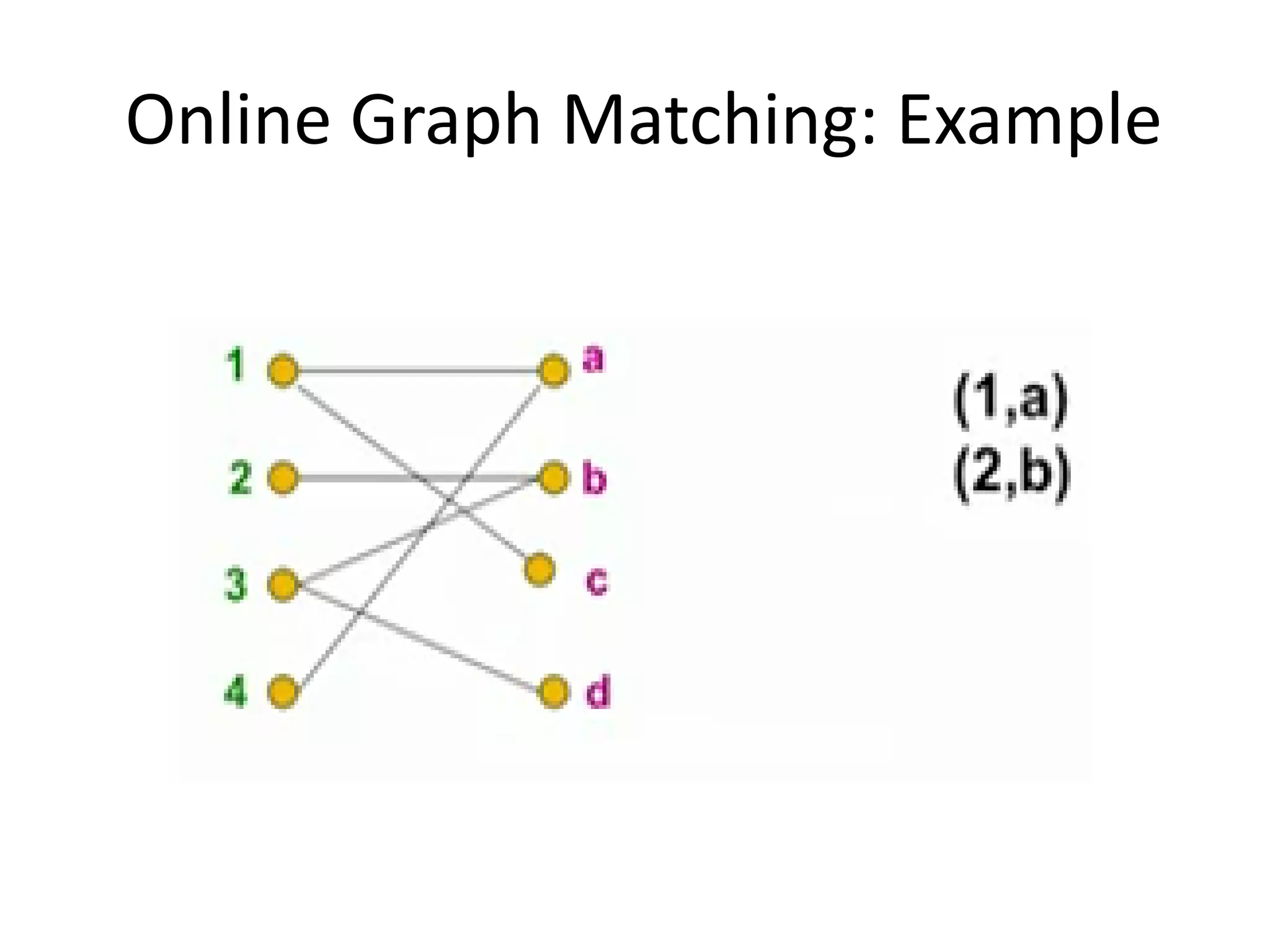
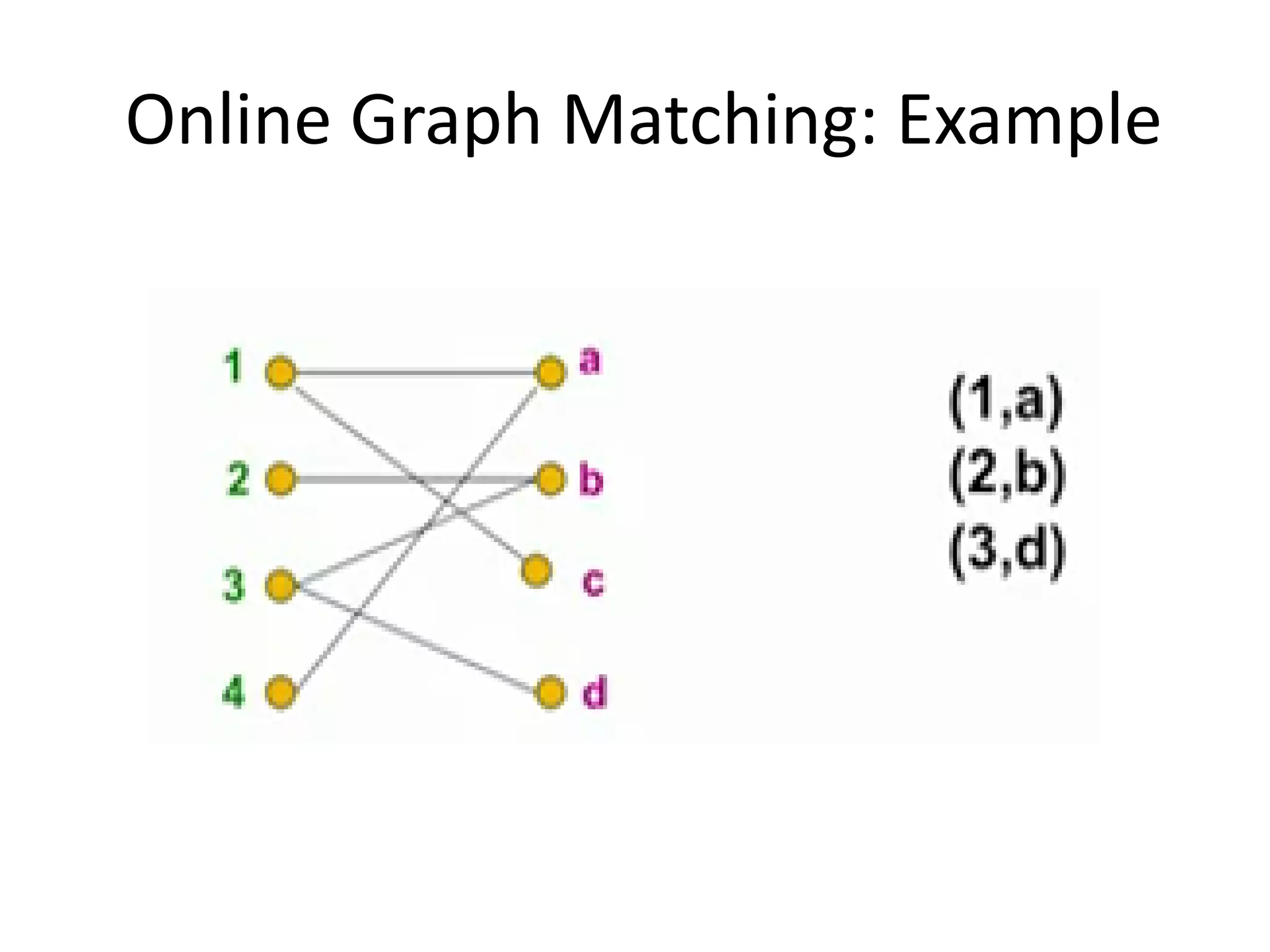
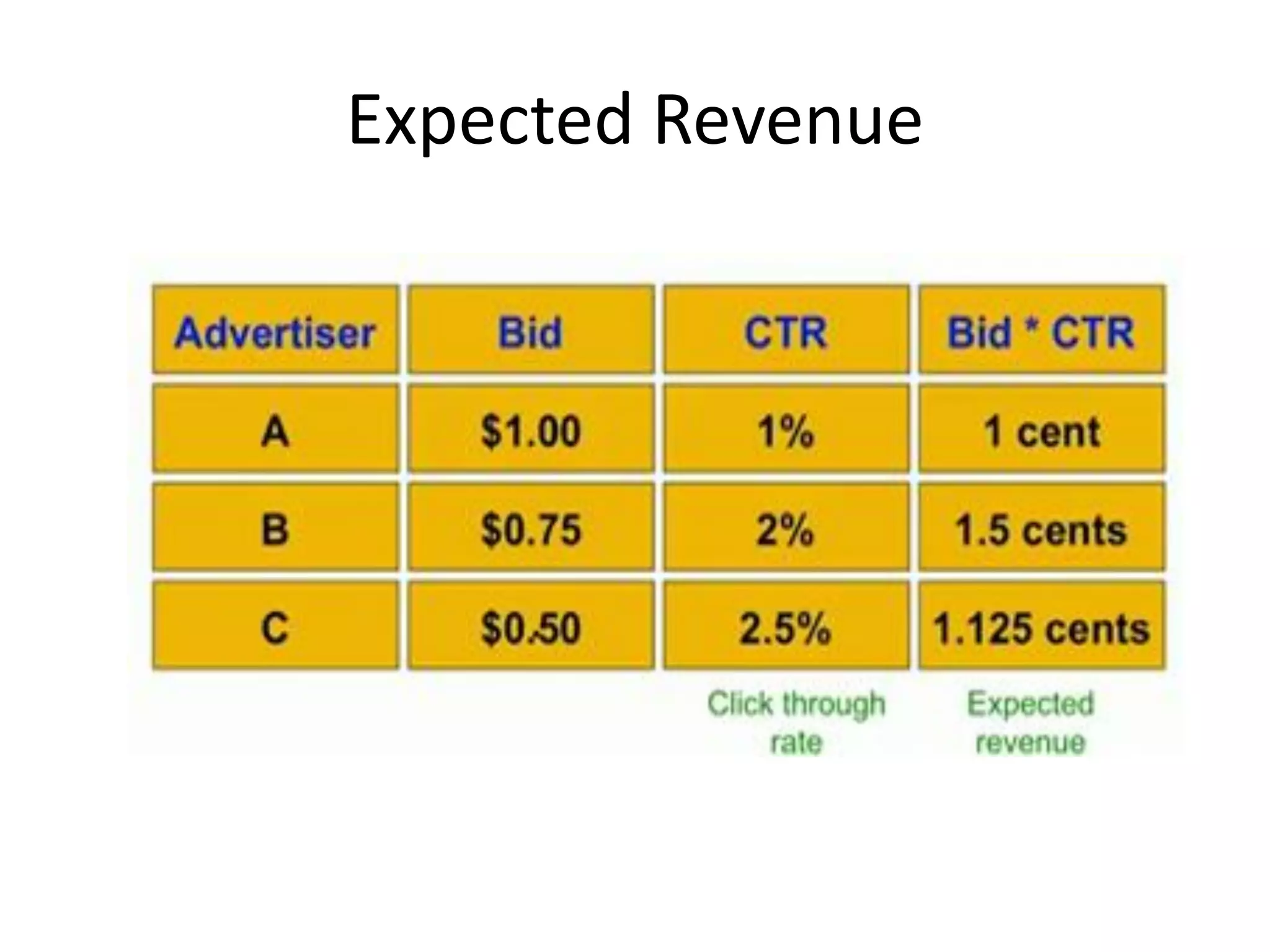
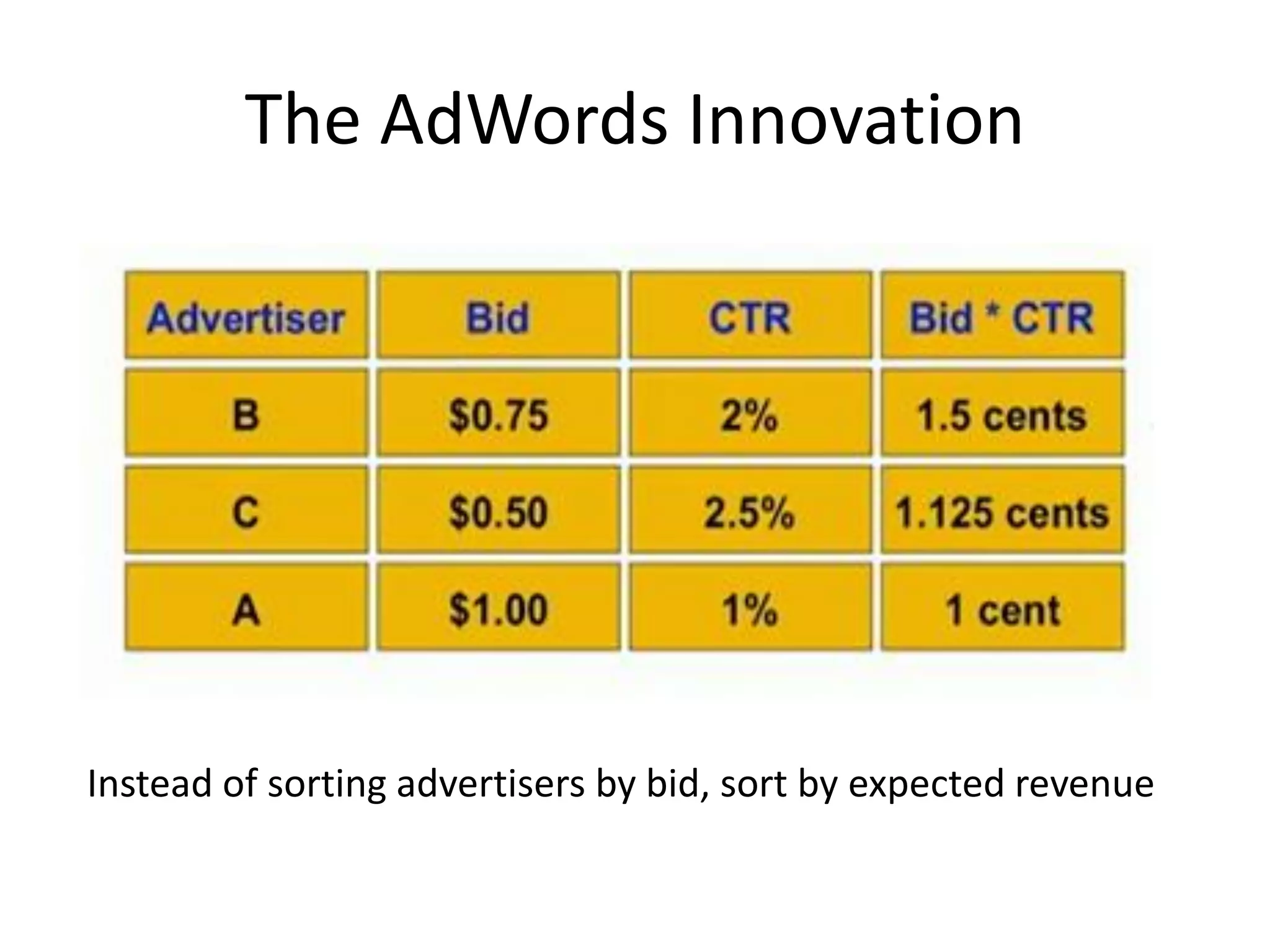
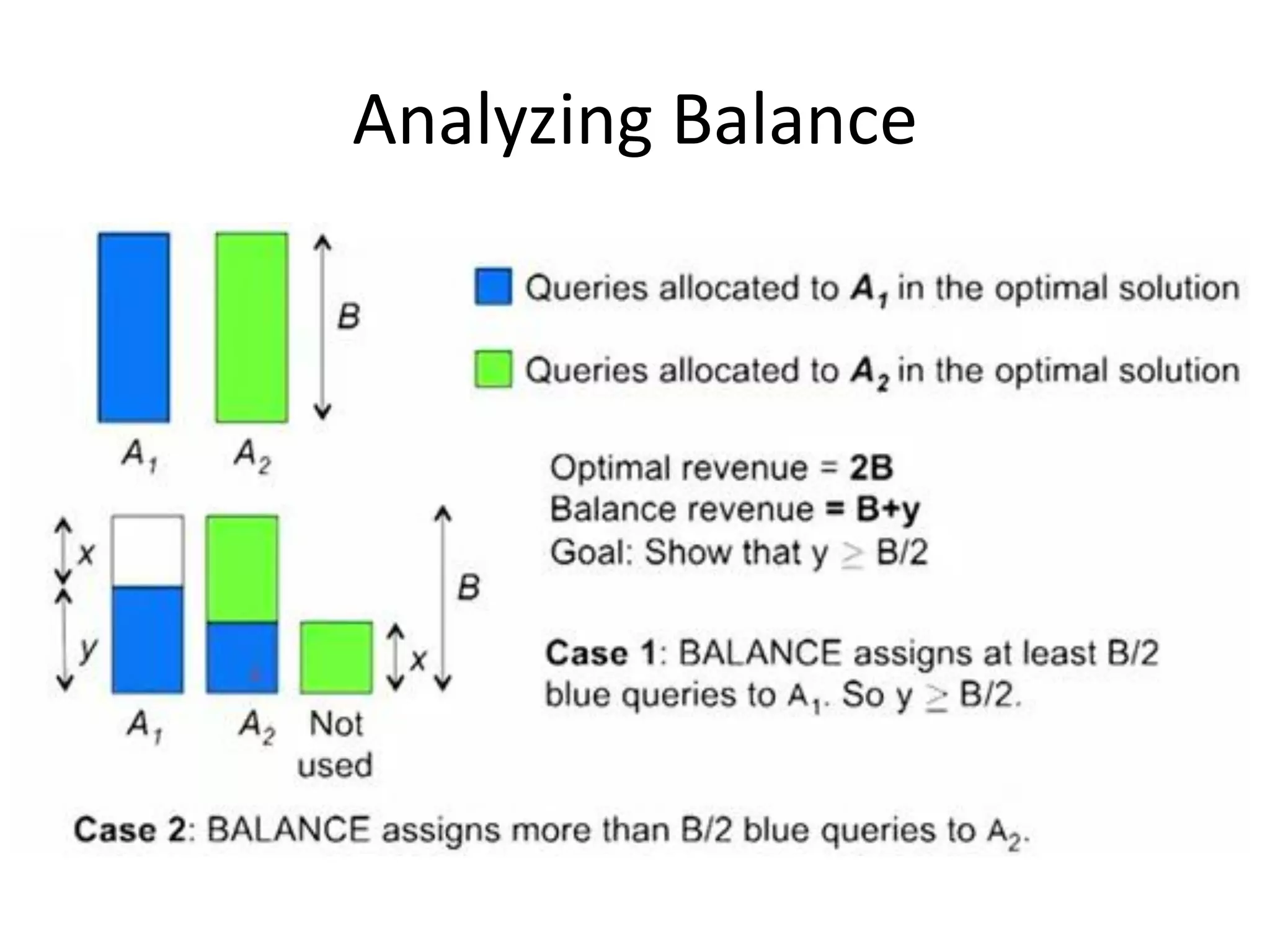
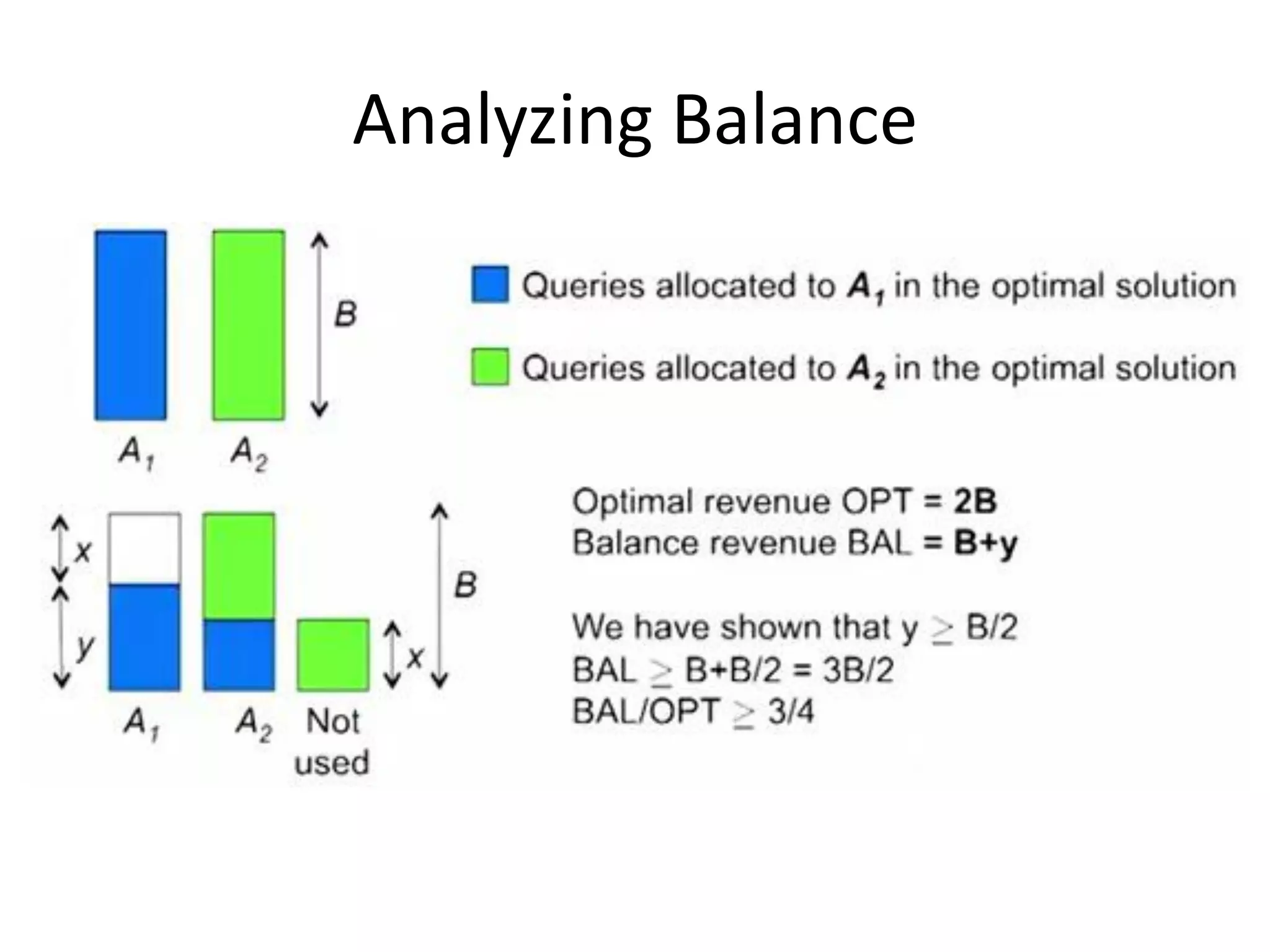
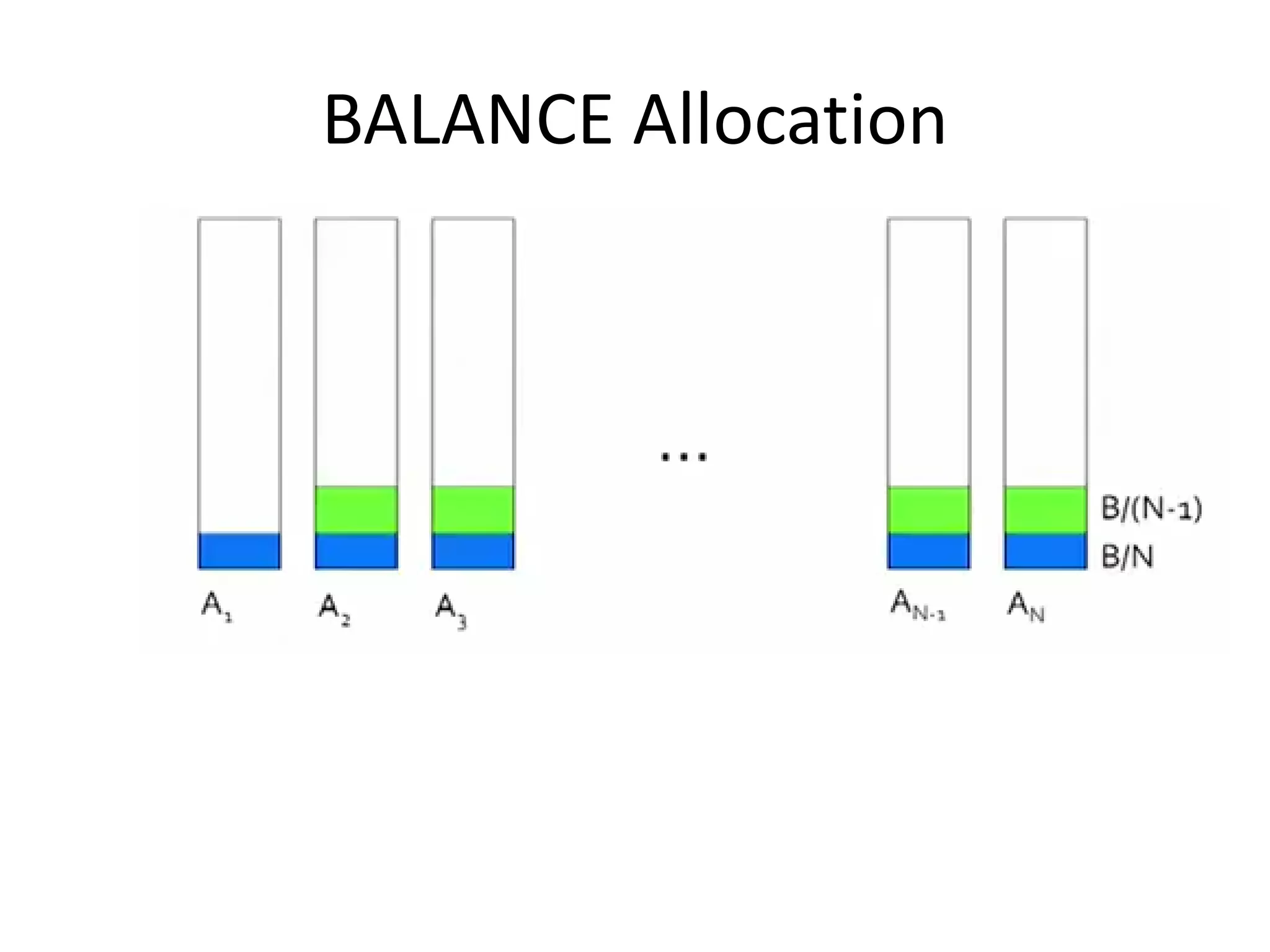
Online algorithms make decisions about an input as it is received piece by piece, as opposed to offline algorithms which receive the full input upfront. The online bipartite matching problem involves matching boys and girls as their compatibility information arrives. A greedy algorithm matches each new girl to an eligible boy, achieving a 1/2 competitive ratio. The AdWords problem involves selecting ads to display for search queries while maximizing revenue. The Balance algorithm deals with advertisers having limited budgets by selecting ads from bidders with the largest remaining budget at each step, achieving a 1-1/e competitive ratio.

2. Online Algorithms
• Classic model of algorithms
– We get to see the entire input, then compute some
function of it
– In this context, “offline algorithm”
• Online Algorithms
– We get to see the input one piece at a time, and need
to make irrevocable decisions along the way
– Similar to the data stream model

3. Example: Bipartite Matching
Nodes: Boys and Girls; Edges: Compatible Pairs
Goal: Match as many compatible pairs as possible

4. Example: Bipartite Matching

5. Example: Bipartite Matching
Perfect matching... all the vertices of graph are matched
Maximum Matching... a matching that contains the longest possible number of matches

6. Matching Algorithm
• Problem: Find a maximum matching for a
given bipartite graph
– A perfect one if it exists
• There is a polynomial – time offline algorithm
based on augmenting path (Hopcroft & Karp
1973)

7. Online Graph Matching Problem
• Initially, we are given the sets boys and girls
• In each round, one girl’s choice are revealed
– That is, girl’s edges are revealed
• At that time, we have to decide either:
– Pair the girl with a boy
– Do not pair the girl with any boy
• Example of application:
Assigning tasks to servers

8. Online Graph Matching: Example

9. Online Graph Matching: Example

10. Online Graph Matching: Example

11. Online Graph Matching: Example

12. Online Graph Matching: Example

13. Online Graph Matching: Example

14. Online Graph Matching: Example

15. Online Graph Matching: Example

16. Greedy Algorithm
• Greedy algorithm for the online graph
matching problem:
– Pair the new girl with any eligible boy
• If there is none, do not pair girl
• How good is the algorithm?

17. Competitive Ratio
• For input I, suppose greedy produces
matching 𝑴 𝒈𝒓𝒆𝒆𝒅𝒚 while an optimal matching
is 𝑴 𝒐𝒑𝒕
Competitive ratio=
𝒎𝒊𝒏 𝑎𝑙𝑙 𝑝𝑜𝑠𝑠𝑖𝑏𝑙𝑒 𝑖𝑛𝑝𝑢𝑡𝑠 𝐼(| 𝑴 𝒈𝒓𝒆𝒆𝒅𝒚|/ |𝑴 𝒐𝒑𝒕|)

18. Analyzing the Greedy Algorithm
• Suppose 𝑴 𝒈𝒓𝒆𝒆𝒅𝒚 ≠ 𝑴 𝒐𝒑𝒕
• Consider the set G of girls
matched 𝑴 𝒐𝒑𝒕 but not in 𝑴 𝒈𝒓𝒆𝒆𝒅𝒚
• (1) |𝑴 𝒐𝒑𝒕| ≤ |𝑴 𝒈𝒓𝒆𝒆𝒅𝒚|+|G|
• Every boy B adjacent to girls in G
is already matched in 𝑴 𝒈𝒓𝒆𝒆𝒅𝒚
• (2) |𝑴 𝒈𝒓𝒆𝒆𝒅𝒚|≥ |B|
• Optimal matches all the girls in G to boys in B
• (3) |G|≤|B|

19. Analyzing the Greedy Algorithm
Combining (2) and (3):
• (4) |G|≤|B|≤ |𝑴 𝒈𝒓𝒆𝒆𝒅𝒚|
Combining (1) and (4):
|𝑴 𝒐𝒑𝒕| ≤ |𝑴 𝒈𝒓𝒆𝒆𝒅𝒚|+|𝑴 𝒈𝒓𝒆𝒆𝒅𝒚|
|𝑴 𝒐𝒑𝒕| ≤ 2|𝑴 𝒈𝒓𝒆𝒆𝒅𝒚|
|𝑴 𝒈𝒓𝒆𝒆𝒅𝒚|/ |𝑴 𝒐𝒑𝒕|≥1/2

20. History of Web Advertising
• Banner ads (1995-2001)
– Initial form of web advertising
– Popular websites charged X$
for every 1000 “impressions”
of the add
• Called “CPM” rate (cost per thousand impressions)
• Modeled similar to TV, magazine ads
– From untargeted to demographically targeted
– Low click-through rates
• Low ROI for advertisers

21. Performance-based Advertising
• Introduced by Overture around 2000
– Advertisers bid on search keywords
– When someone searches for that keyword, the
highest bidder’s ad is shown
– Advertiser is charged only if the ad is clicked on
• Similar model adopted by Google with some
changes around 2002
– Called Adwords

22. Algorithmic Challenges
• Performance – based advertising works
– Multi-billion-dollar industry
• What ads to show for a given query?
– The AdWords Problem Mining of Massive Datasets
• If I am an advertiser, which search terms should I
bid on and how much should I bid?
– (It’s not our focus)

23. AdWords Problem
• A stream of queries arrives at the search
engine: 𝑞1, 𝑞2, …
• Several advertisers bid on each query
• When query 𝑞𝑖 arrives, search engine must
pick a subset of advertisers whose ads are
shown
• Goal: Maximize search engine’s revenues
• Clearly we need an online algorithm!

24. Expected Revenue

25. Expected Revenue

26. The AdWords Innovation
Instead of sorting advertisers by bid, sort by expected revenue

27. Limitations of Simple Algorithm
• CTR of an ad is unknown
• Advertisers have limited budgets and bid on
multiple ads.

28. Future Work
• Estimation of CTR
• Algorithm to solve limited budgets problem
(Balance Algorithm)

29. Recall…
• Greedy algorithm for the online graph
matching problem
• Competitive Ratio
• History of Web Advertising
• Performance-based Advertising
• The AdWords Innovation
• Click Through Rate (CTR)
• Expected Revenue

30. AdWords Problem
Given:
• A set of bids by advertiser for search queries
• A click-through rate for each advertiser query
pair
• A budget for each advertiser
• A limit on the number of ads to be displayed
with each search query

31. Adwords Problem
Respond to each search query with a set of
advertisers such that:
• The size of set is no larger than the limit on
the number of ads per query
• Each advertiser has bid on search query
• Each advertiser has enough budget left to pay
for the ad if it is clicked upon

32. Dealing with Limited Budget
• Our setting: Simplified Environment
– There is 1 ad shown for each query
– All advertisers have same budget B
– All ads are equally likely to be clicked
– Value of each ad is same(=1)
• Simplest Algorithm is greedy
– For a query pick any advertiser who has bid 1 for
that query
– Competitive ratio of greedy is 1/2.

33. Bad Scenario for Greedy
• Two advertisers A and B
– A bids on x, B bids on x and y
– Both have budget $4
• Query stream: x x x x y y y y
– Worst case for greedy choice: B B B B _ _ _ _
– Optimal: A A A A B B B B
– Competitive ratio= ½
• This is worst case!
– Note: Greedy algorithm is deterministic – it always
resolves draw in same way

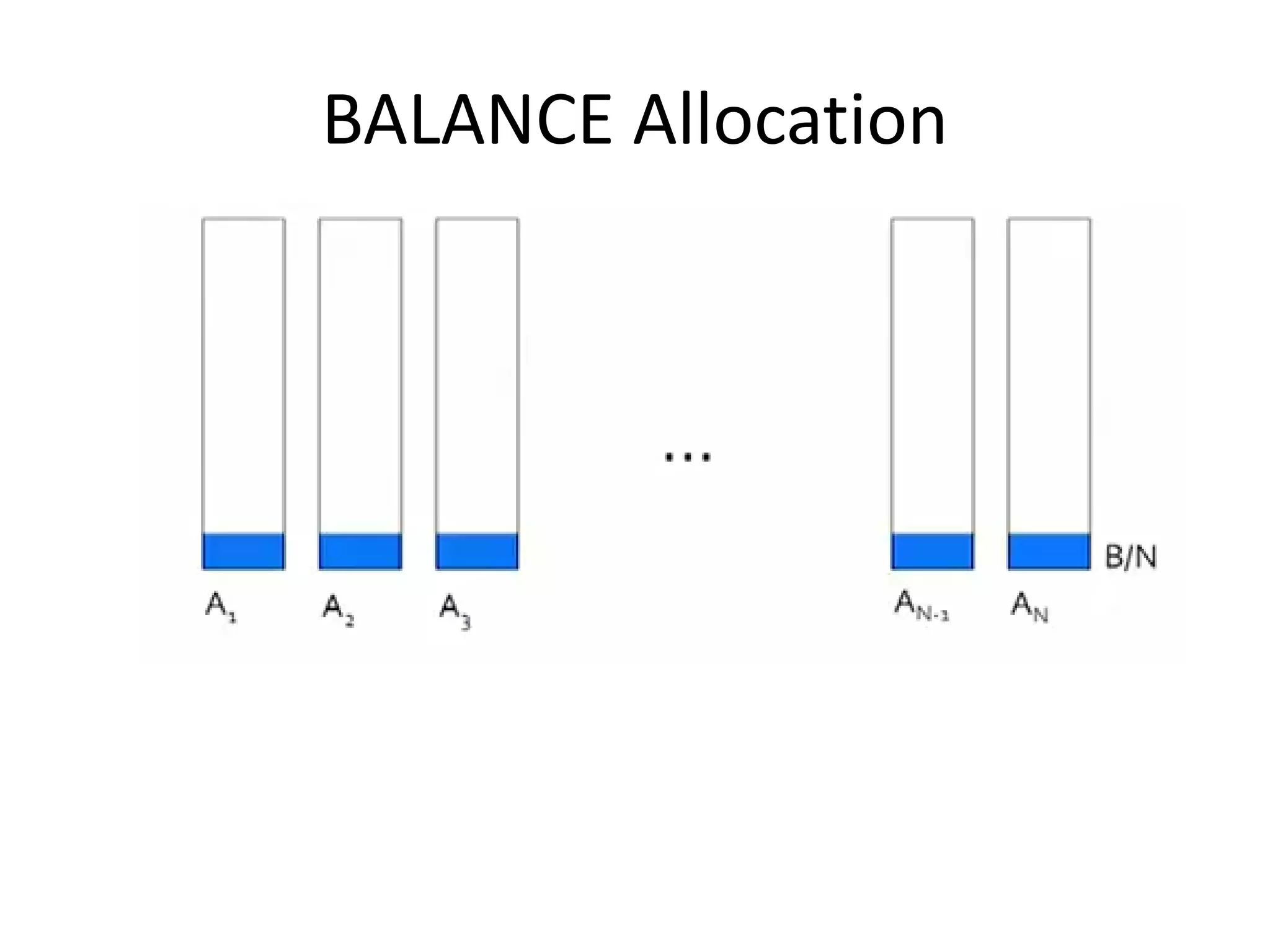
34. BALANCE Algorithm [MSVV]
• For each query, pick the advertiser with the
largest unspent budget
• Break ties arbitrarily ( but in deterministic way)

35. Example: BALANCE
• Two advertisers A and B
– A bids on x, B bids on x and y
– Both have budget $4
• Query stream: x x x x y y y y
• Balance Choice: A B A B B B _ _
– Optimal: A A A A B B B B
• Competitive ratio= ¾
– For BALANCE with two advertisers

36. Analyzing 2 advertiser BALANCE
• Consider simple case
– 2 Advertisers, 𝐴1 and 𝐴2, each with budget B(≥1)
– Optimal solution exhaust both advertisers’ budgets
• BALANCE must exhaust at least one advertiser’s
budget:
– If not, we can allocate more queries
– Assume BALANCE exhausts 𝐴2’s budget

37. Analyzing Balance

38. Analyzing Balance

39. BALANCE: General Result
• In the general case, worst case competitive
ratio of BALANCE is 1-1/e = approx. 0.63
– Interestingly, no online algorithm has a better
competitive ratio!
• Let’s see the worst case example that gives
this ratio

40. Worst case for BALANCE
• N advertisers 𝐴1, 𝐴2, … 𝐴 𝑁
– Each with budget B>N
• Queries:
– N.B queries appear in N rounds of B queries each
• Bidding:
– Round 1 queries: bidders 𝐴1, 𝐴2, … 𝐴 𝑁
– Round 2 queries: bidders 𝐴2, 𝐴3, … 𝐴 𝑁
– Round i queries: bidders 𝐴𝑖, … 𝐴 𝑁

41. BALANCE Allocation

42. BALANCE Allocation

43. BALANCE Allocation

44. BALANCE Allocation
After k rounds, the allocation to k advertiser is:
𝑆 𝑘 = 𝐵 (𝑁 − 𝑖 + 1)𝑘
𝑖=1
If we find smallest k such that 𝑆 𝑘 ≥ 𝐵, then after k rounds
we can not allocate any queries to any advertiser

45. BALANACE Analysis

46. BALANACE Analysis
• Fact for large n
– Result due to Euler
ln 𝑁 − 𝑘 = ln 𝑁 − 1
ln(𝑁/(𝑁 − 𝑘)) = 1
𝑁/(𝑁 − 𝑘) = 𝑒
𝒌 = 𝑵(𝟏 − 𝟏/𝒆)

47. BALANACE Analysis
• So after the first 𝑘 = 𝑁(1 − 1/𝑒) rounds, we
cannot allocate a query to any advertiser
• Revenue = 𝐵. 𝑁(1 − 1/𝑒)
• Competitive ratio = 1 − 1/𝑒

48. General Version of the Problem
• So far: all bid = 1, all budget equal (=B)
• In general balance can be terrible
– Consider query q, two advertiser 𝐴1and 𝐴2
– 𝐴1: bid = 1, budget = 110
– 𝐴2: bid = 10, budget = 100
– Suppose we see 10 instance of q
– BALANCE always selects 𝐴1and earns 10
– Optimal earns 100

49. Generalized BALANCE
• Consider query q, bidder i
– Bid = 𝑥𝑖
– Budget = 𝑏𝑖
– Amount spent so far = 𝑚𝑖
– Fraction of budget left over 𝑓𝑖 = 1 − 𝑚𝑖/𝑏𝑖
– Define 𝜑𝑖(𝑞) = 𝑥𝑖 1 − 𝑒−𝑓 𝑖
• Allocate query q to bidder i with largest value
of 𝜑𝑖 𝑞
• Same Competitive ratio = 1 − 1/𝑒

50. Conclusion
• AdWords Problem
• Limited Budget Problem
• Solution of Limited Budget Problem
– BALANCE Algorithm and Analysis

51. Future Work
• Estimation of CTR
– Data Mining and Machine Learning techniques

52. References
• [1] Mehta A, Saberi A, Vazirani U, Vazirani V.
Adwords and generalized online
matching. J ACM (JACM) 2007;54(5):22.
• [2] Reiss C, Wilkes J, Hellerstein JL. Google cluster-
usage traces: formatþ schema.
Google Inc., White Paper; 2011.
• [3] Legrain A, Fortin M-A, Lahrichi N, Rousseau L-
M. Online stochastic optimization of radiotherapy
patient scheduling. In: Health care management
science;
2014. p. 1–14

53. References
• [4] Coy P. The secret to google's success.
〈http://www.bloomberg.com/bw/stories/ 2006-03-05/
the-secret-to-googles-success〉;
5 March 2006 [accessed16.02.15].
• [5] Google, 2014. 2014 financial tables.
〈https://investor.google.com/financial/tables.html〉
[accessed 16.02.2015].
• [6] Antoine Legrain , Patrick Jaillet A stochastic
algorithm for online bipartite resource allocation
problems.
Computers & Operations Research 75 (2016) 28–37,

54. Thank you