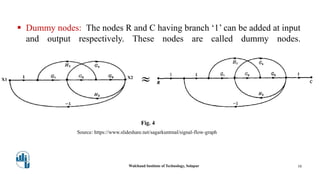
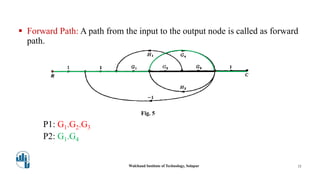
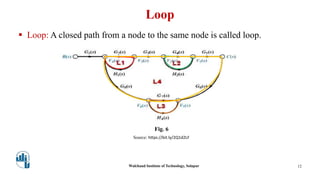
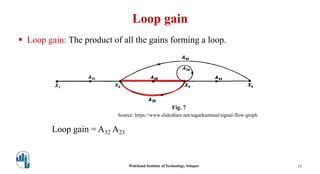
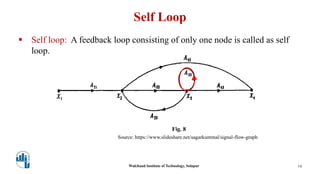
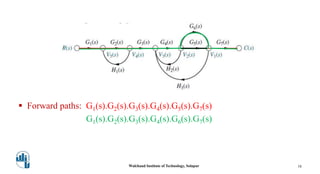
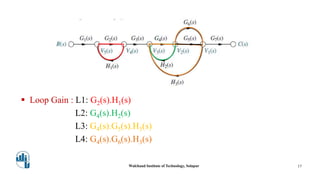
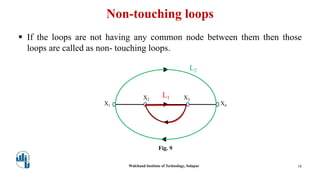
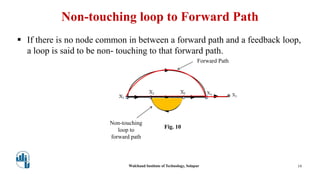
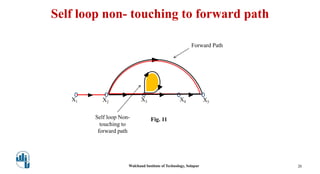
This document provides an overview of signal flow graphs. It defines key concepts like nodes, branches, paths, loops, and loop gains. Examples are given to illustrate these concepts, such as a simple voltage-current-resistance circuit and its corresponding signal flow graph. Different types of nodes, paths, and loops are defined, including forward paths, self loops, and non-touching loops. The document serves as an introduction to representing physical systems as signal flow graphs.

1. Signal Flow Graph
Ms. Priyanka P. Bidla
(birla.priyanka@gmail.com)
Assistant Professor, Electronics & Telecommunication Engg.
Walchand Institute of Technology, Solapur
(www.witsolapur.org)

2. Learning Outcome
Students will be able to represent a given physical system into signal
flow graph(SFG).
Walchand Institute of Technology, Solapur 2
At the end of this session,

3. Contents
 Introduction
 Definitions
 Terminologies
 Examples
Walchand Institute of Technology, Solapur 3

4. Introduction
 The graphical representation of the variables of a set of linear algebraic
equations representing the system is called Signal Flow Graph
Representation.
 SFG shows the flow of signals from one point of a system to another and
which gives the relationships among the signals.
 A signal-flow graph consists only of branches, which represent signals
and nodes.
Walchand Institute of Technology, Solapur 4

5.  Consider a simple equation,
V = I.R
V : Voltage; I: Current ; R: Resistance
 The signal flow graph of the equation is shown below
I V
R
Walchand Institute of Technology, Solapur 5
Fig. 1

6. Contd..
 All the dependent and independent variables are represented by the nodes.
 The relationship between various nodes are represented by joining the nodes
as per the equations.
Walchand Institute of Technology, Solapur 6

7. Definitions
 Nodes: SFG represents by small circles called Nodes.
 Branches :- Line joining two nodes is called Branch.
The branches are always unidirectional.
Walchand Institute of Technology, Solapur 7
I V
R
BranchNodes
Fig. 2

8. Terminologies
 Input / Source Node: A node has only outgoing branches is known as
source/input node.
 Output/ Sink Node: A node has only incoming branches is known as
sink/output node.
 Chain Node: A node has incoming and outgoing branches is known as
chain node.
Walchand Institute of Technology, Solapur 8

9. Path
 Path: A path is defined as a traversal of connected branches in the direction
of branch arrow.
 Path gain: Path gain is defined as the product of all branch gains while
going through the forward path .
Path gain: A12 x A23
Walchand Institute of Technology, Solapur 9
X1 X2 X3
A23A12
Fig. 3

10.  Dummy nodes: The nodes R and C having branch ‘1’ can be added at input
and output respectively. These nodes are called dummy nodes.
Fig. 4
Source: https://www.slideshare.net/sagarkuntmal/signal-flow-graph
Walchand Institute of Technology, Solapur 10
X1 X2

11.  Forward Path: A path from the input to the output node is called as forward
path.
P1: G1.G2.G3
P2: G1.G4
Walchand Institute of Technology, Solapur 11
Fig. 5

12. Loop
 Loop: A closed path from a node to the same node is called loop.
Walchand Institute of Technology, Solapur
Fig. 6
Source: https://bit.ly/2Q1d2LF
12

13. Loop gain
 Loop gain: The product of all the gains forming a loop.
Walchand Institute of Technology, Solapur
Fig. 7
Source: https://www.slideshare.net/sagarkuntmal/signal-flow-graph
Loop gain = A32 A23
13

14. Self Loop
 Self loop: A feedback loop consisting of only one node is called as self
loop.
Walchand Institute of Technology, Solapur 14
Fig. 8
Source: https://www.slideshare.net/sagarkuntmal/signal-flow-graph

15. Think and Write
Consider the signal flow graph below and identify the following
1] Forward paths
2] Loops
3] Loop gain
Walchand Institute of Technology, Solapur 15

16.  Forward paths: G1(s).G2(s).G3(s).G4(s).G5(s).G7(s)
G1(s).G2(s).G3(s).G4(s).G6(s).G7(s)
Walchand Institute of Technology, Solapur 16

17.  Loop Gain : L1: G2(s).H1(s)
L2: G4(s).H2(s)
L3: G4(s).G5(s).H3(s)
L4: G4(s).G6(s).H3(s)
Walchand Institute of Technology, Solapur 17

18. Non-touching loops
 If the loops are not having any common node between them then those
loops are called as non- touching loops.
Walchand Institute of Technology, Solapur 18
X1
L2
Fig. 9
L1
X4
X3X2

19. Non-touching loop to Forward Path
 If there is no node common in between a forward path and a feedback loop,
a loop is said to be non- touching to that forward path.
X5
X4
Forward Path
Non-touching
loop to
forward path
Walchand Institute of Technology, Solapur 19
Fig. 10

20. Self loop non- touching to forward path
Walchand Institute of Technology, Solapur 20
X1
Fig. 11
X4X3X2 X5
Forward Path
Self loop Non-
touching to
forward path

21. References
1] Control Systems Engineering I. J. Nagrath & M Gopal New Age
International Publication(5th Edition)
2] https://www.slideshare.net/sagarkuntmal/signal-flow-graph
3] https://image.slidesharecdn.com/signalflowgraphexamples-150415045856-
conversion-gate01/95/signal-flow-graph-9-638.jpg?cb=1451886608
21Walchand Institute of Technology, Solapur

22. Thank you
Walchand Institute of Technology, Solapur 22