Downloaded 59 times
![Label Propagation
Least square Solution
S Here comes the first Equation , Lets define
S Matrix W (NxN) , Similarity Between Objects
S Matrix D (NxN), degree of each Object
S Matrix L (Laplacian Matrix) = D – W
S Label vector F (Nx1), assignment of each object [-1,1] and
not {-1,1}
S Objective Function Min ½](https://image.slidesharecdn.com/semi-supervisedlearning-140304091308-phpapp02/85/Semi-supervised-learning-13-320.jpg)
Uploaded byAhmed Taha
Semi supervised learning
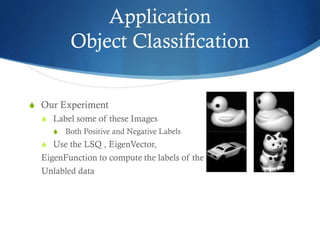
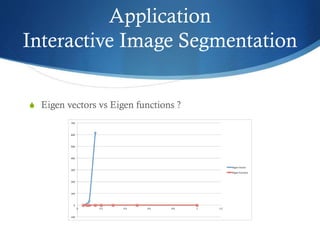
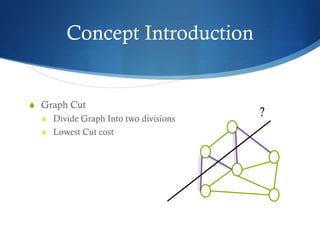
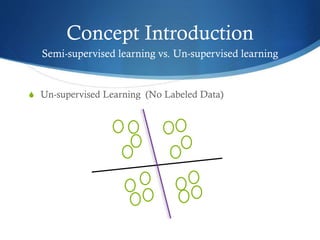
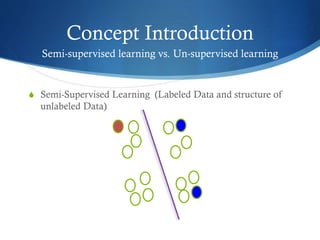
The document discusses semi-supervised learning techniques, focusing on graph cut and least square solutions as methods for object classification and image segmentation. It distinguishes between semi-supervised and unsupervised learning, presenting the use of eigenvectors and eigenfunctions for dimensionality reduction and navigating high-dimensional data. The findings suggest using eigenvectors for smaller object sets with high dimensions and eigenfunctions for larger sets with lower dimensions for optimal performance.
More Related Content
![[Review] BoxInst: High-Performance Instance Segmentation with Box Annotations...](https://cdn.slidesharecdn.com/ss_thumbnails/boxinstreviewcdm-210627063153-thumbnail.jpg?width=640&height=640&fit=bounds)
Semi supervised learning
- 1.
- 2. Content S Concept Introduction SGraph cut and Least Square solution S Eigen vector and Eigen Functions S Application
- 3. Concept Introduction S GraphCut S Divide Graph Into two divisions S Lowest Cut cost ?
- 4. Concept Introduction S DegreeMatrix / variation
- 5. Concept Introduction S ObjectRepresentation S 2D Point S 3D Point S Pixel S Or even a Whole Image S It is ALL nodes and Edges
- 6. Concept Introduction Semi-supervised learningvs. Un-supervised learning S Un-supervised Learning (No Labeled Data)
- 7. Concept Introduction Semi-supervised learningvs. Un-supervised learning S Semi-Supervised Learning (Labeled Data and structure of unlabeled Data)
- 8. Graph Cut Least squareSolution S Semi-Supervised Learning (Labeled Data) S We have 3 Objects Now This Should be a Fully Connected Graph
- 9. Graph Cut Least squareSolution S Objective separate graph into two part S (Red and Non-Red) S Size if this Matrix is S N^2 S Not sparse This Should be a Fully Connected Graph
- 10. Graph Cut Least squareSolution S We can after that divide the rest of graph into blue and not blue and so on S NP Problem ? This Should be a Fully Connected Graph
- 11. Graph Cut Least squareSolution S Current Situation , we have a fully connected Graph , represented in NxN Matrix = W (Similarity Matrix) S We expect each object to be assigned {1,-1} {Red, non- red} with lowest cost assignment cost S But this is NP ???
- 12. Label Propagation Least squareSolution S Weighted Average concept S New Node S (Red Now)1 * 1 S (Blue) -1 * 0.1 S Green -1 * 0.2 S 1-0.1-0.2 = 0.7 , S so it is probably a Red Object {1} 1 0.1 0.2
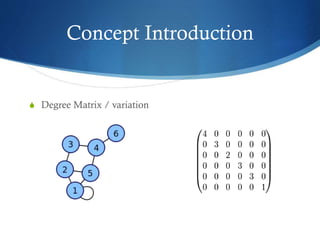
- 13. Label Propagation Least squareSolution S Here comes the first Equation , Lets define S Matrix W (NxN) , Similarity Between Objects S Matrix D (NxN), degree of each Object S Matrix L (Laplacian Matrix) = D – W S Label vector F (Nx1), assignment of each object [-1,1] and not {-1,1} S Objective Function Min ½
- 14. Least square Solution SObjective Function Min ½ S But this doesn't’t consider Label data yet S After some Equation manipulation
- 15. Least square Solution SWe need to solve NxN S NxN matrix Inverse S NxN matrix multiplication S Need to reduce dimensions by using Eigenvectors of Graph Laplacian
- 16. EigenVector S As mentionedbefore we want to have a Label vector f S f = α U , so once we have U, we can get α and then we get f S Laplacian Eigenmap dimension reduction S L have the characteristic is this Graph 1 0.1 S Mapping the objects into a new dimension 0.2
- 17. EigenVector S As mentioned beforewe want to have a Label vector f S Get the EigenVectors (U) of Laplacian Matrix (L) S f = α U , so once we have U, we can get α and then we get f S We still need to work with NxN Matrix, at least we compute its Eigen vectors
- 18. Eigen Function S Eigenfunctionare limit of Eigenvectors as n ∞ S For each dimension (2), S we calculate the Eigenvector by interpolating the Eigen function from the histogram of this dimension S Which takes a lot less than S Need more explanation
- 19. Eigen Function S Eigenfunctionare limit of Eigenvectors as n ∞ S Notice solution of Eigenfunction is based on the number of Dimensions, while Eigenfunction is based on number of Objects S Images Pixels as Object S Images with local features as dimension
- 20. Application S Object Classification SInteractive Image segmentation S Image Segmentation
- 21. Application Object Classification S Coil20 Dataset S 20 Different Object S Each Object has 72 different pose
- 22. Application Object Classification S OurExperiment S Label some of these Images S Both Positive and Negative Labels S Use the LSQ , EigenVector, EigenFunction to compute the labels of the Unlabled data
- 23. Application Object Classification S OurResults LSQ Solution EigenVector Solution Eigenfunction Solution
- 24. Application Object Classification S ResultsAnalysis S LSQ solution is almost perfect since it is almost exact Solution S EigenVector generate approximate solution but in less time, which makes more sense it is just solving one NxN Matrix to get Eigen Vectors S Eigen Function method also generated an approximate solution but its time was worse
- 25. Application Object Classification S TimeResults Analysis
- 26. Application Object Classification S ResultsExplanation S We have 4 (Object) * 36 (pose per object) so total of 144 Object so Matrix laplaican is of size 144 S Each Image has 128*128 (gray scale) pixel so total of 16384 , so each object have 16384 dimension S 144 Object vs 16384 dimension
- 27. Application Object Classification S ResultsExplanation S 144 Object vs 16384 dimension S So it is expected that LSQ , EigenVector method to finish faster since Matrix L is not that big S While Eigen-function will take a long time to compute the Eigen-function for each dimension 16384
- 28. Application Interactive Image Segmentation SWhy it is called Interactive
- 29. Application Interactive Image Segmentation SWe now have 500x320 = 160000 Object S But each object have like 5 dimension (R,G,B,X,Y). S Eigen vectors vs Eigen functions ?
- 30. Application Interactive Image Segmentation SEigen vectors vs Eigen functions ?
- 31. Application Interactive Image Segmentation SEigen vectors vs Eigen functions ? S No Way LSQ or Eigen vectors can support such number of objects , Laplacian Matrix size is 160000 x 160000. S Eigen function method calculates Eigen vectors of 5 dimensions and we are ready to show some results
- 32.
- 33. Application Interactive Image Segmentation SNotice why bears have distinctive colors from the rest of the image, but this is still in progress work. S It is not perfect yet
- 34. Application S Non-Interactive segmentation SFore-ground background segmentation S Co-segmentation S System held user to know where to add annotation
- 35. Conclusion S It isbetter to use Eigen vectors when you have small set of objects with high dimension S It is better to use Eigen functions when you have big set of objects with small dimension
- 36.