This document discusses principal component analysis (PCA), including the theory behind it and toolkits for implementing it. The theory section explains how PCA transforms correlated variables into uncorrelated principal components to perform dimensionality reduction. It describes minimizing squared error to find the principal components, which are the eigenvectors of the covariance matrix. The document lists toolkits for PCA in languages like C, Java, Perl and MATLAB and provides code examples.

1. Theory and Toolkits
of PCA
2009 5/4 IRLab
Study Group
Presenter : Chin-Hui Chen

2. Agenda
 Theory :
◦ 1. Scenario
◦ 2. What is PCA?
◦ 3. How to minimize Squared-Error ?
◦ 4. Dimensionality Reduction
 Toolkit :
◦ A list of PCA toolkits
◦ Demo

3. Scenario (Point? Line?)
 Consider a 2-dimension space
Least Squared Error

4. Agenda
 Theory :
◦ 1. Scenario
◦ 2. What is PCA?
◦ 3. How to minimize Squared-Error ?
◦ 4. Dimensionality Reduction
 Toolkit :
◦ A list of PCA toolkits
◦ Demo

5. What is PCA ? (1)
 Principal component analysis (PCA)
involves a mathematical procedure that
transforms a number of possibly
correlated variables into a smaller number
of uncorrelated variables called “principal
components”.

6. What is PCA ? (2)
 What can PCA do ?
◦ Dimensionality Reduction
 For example :
◦ Assuming N points in D-dim space
◦ e.g. {x1, x2, x3, x4} ; xi = (v1, v2)
◦ A set (M) of basis for projection
◦ e.g. {u1}
 They are orthonormal bases (長度1,兩兩內積0)
 M << D (represent the feature in M dimensions)
◦ e.g. xi = (p1)

7. Agenda
 Theory :
◦ 1. Scenario
◦ 2. What is PCA?
◦ 3. How to minimize Squared-Error ?
◦ 4. Dimensionality Reduction
 Toolkit :
◦ A list of PCA toolkits
◦ Demo

8. How to minimize Squared-Error ?
 Consider a D-dimension space
◦ Given N point : {x1, x2, …, xn}
◦ xi is a D-dim vector
 How to
◦ 1. 找一個點使得squared-error最小
◦ 2. 找一條線使得squared-error最小

9. How to ? - Point
◦ Goal : Find x0 s.t. min.
◦
◦ Let .

10. How to ? – Point - Line
 ∴ x0 =
◦ 1. 找一個點使得squared-error最小
◦ 2. 找一條線使得squared-error最小
 L : xk’- x0 = ake
 xk’= x0 + ake
 = m + ake

11. How to ? – Line
 L : xk’ = m + ake
 Goal :
 Find a1…an


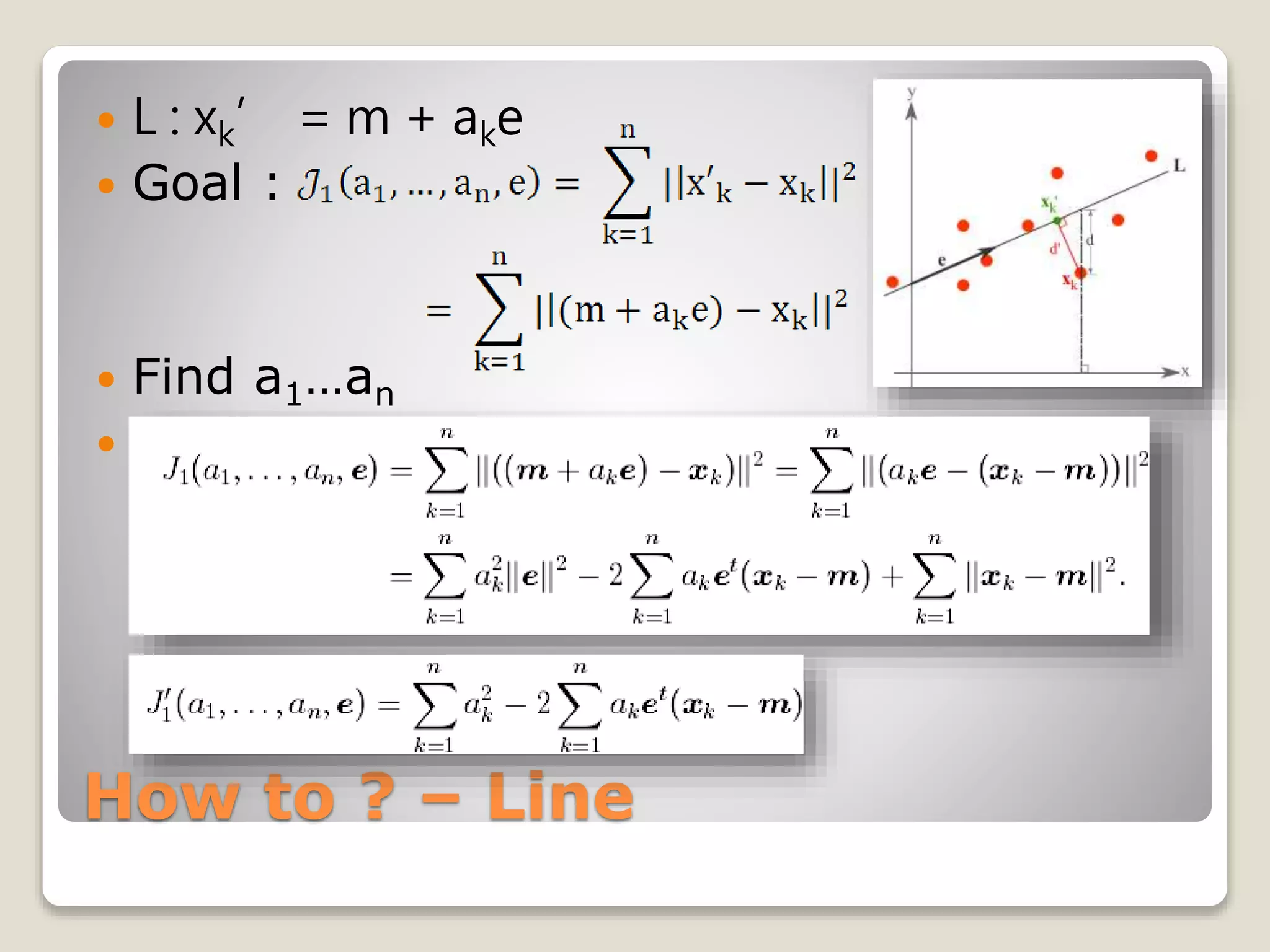
12. How to ? – Line
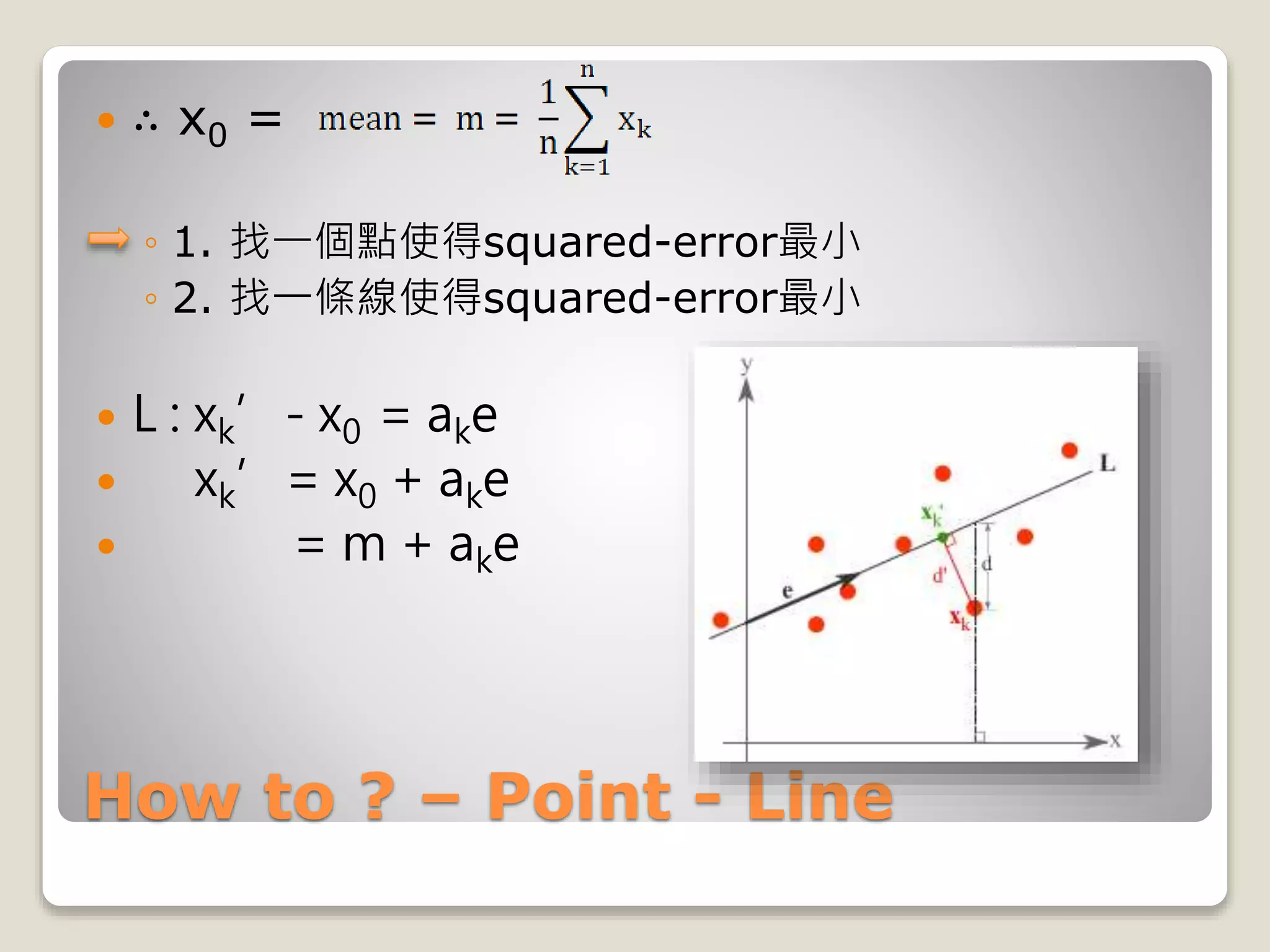
 每個部份微分後 [2ak – 2et(xk-m)]

 What does it mean ?
xk’ = m + ake

13. How to ? – Line
 Then, how about e ?

14. How to ? – Line
 Let
Independent of e

15. How to ? – Line
f(x,y) ->
But if x,y : g(x,y)=0
 J’1(e) = -etSe
 Use lagrange multiplier :

 Because |e| = 1 , u = etSe – λ(ete-1)

16. How to ? – Line

◦ What is S ?
 Covariance Matrix (共變異數矩陣)
◦ Assume D-dim

17. How to ? – Line
 , we know S.
 Then, what is e ? Eigenvectors of S.
AX= λX Eigen : same

18. How to ? – conclusion
 Summary :
◦ Find a line : xk’= m + ake
 ak = et(xk-m)
 Se = λe ; e = eigenvectors of covariance matrix.
◦ D-dim space can find D eigenvectors.

19. Agenda
 Theory :
◦ 1. Scenario
◦ 2. What is PCA?
◦ 3. How to minimize Squared-Error ?
◦ 4. Dimensionality Reduction
 Toolkit :
◦ A list of PCA toolkits
◦ Demo

20. Dimensionality
Reduction

21. Dimensionality Reduction
 Consider a 2-dim space …
X1 = (a,b)
X2 = (c,d)
X1 = (a’,b’)
X2 = (c’,d’)
We are going to do …
X1 = (a’)
X2 = (c’)

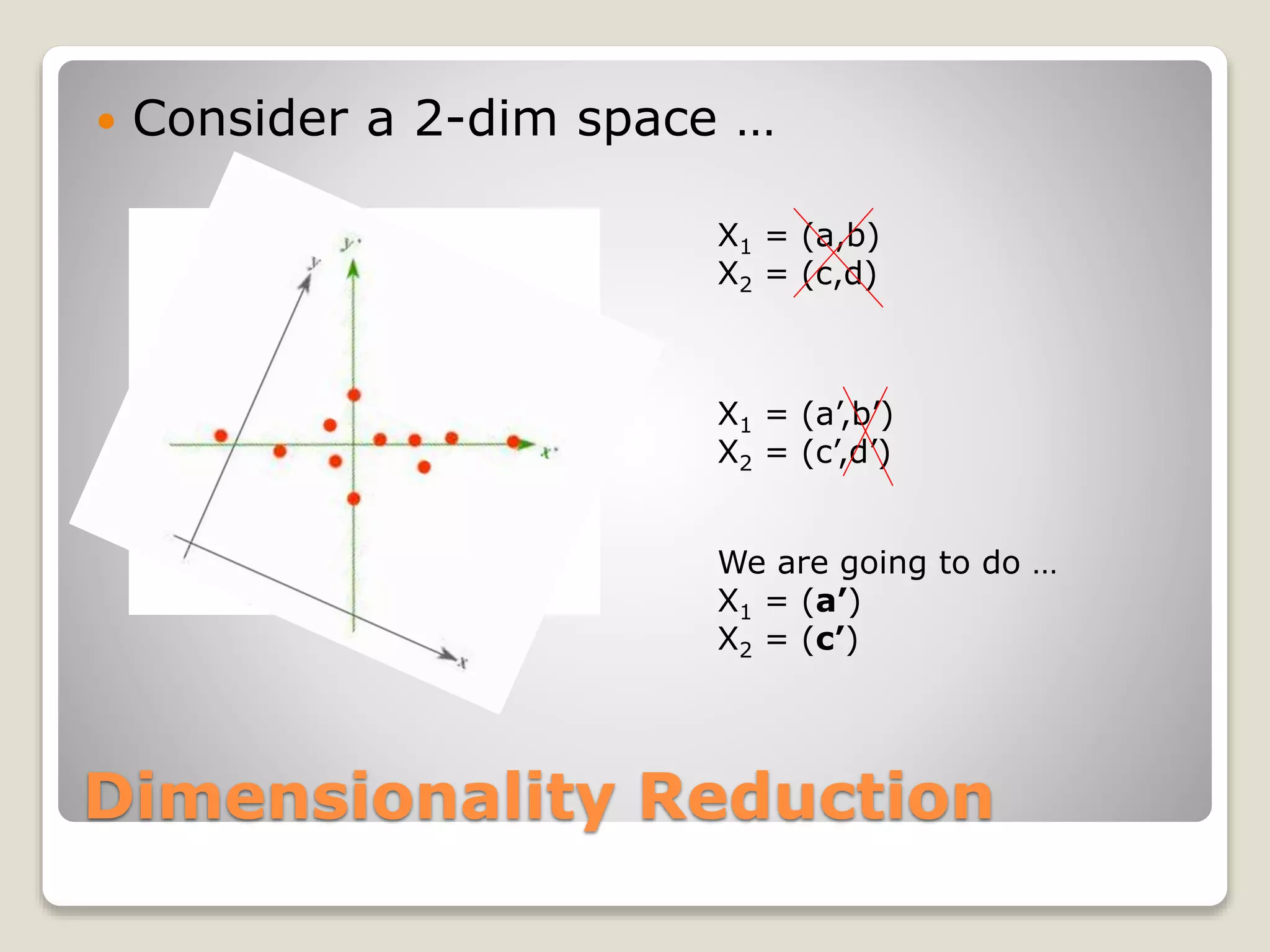
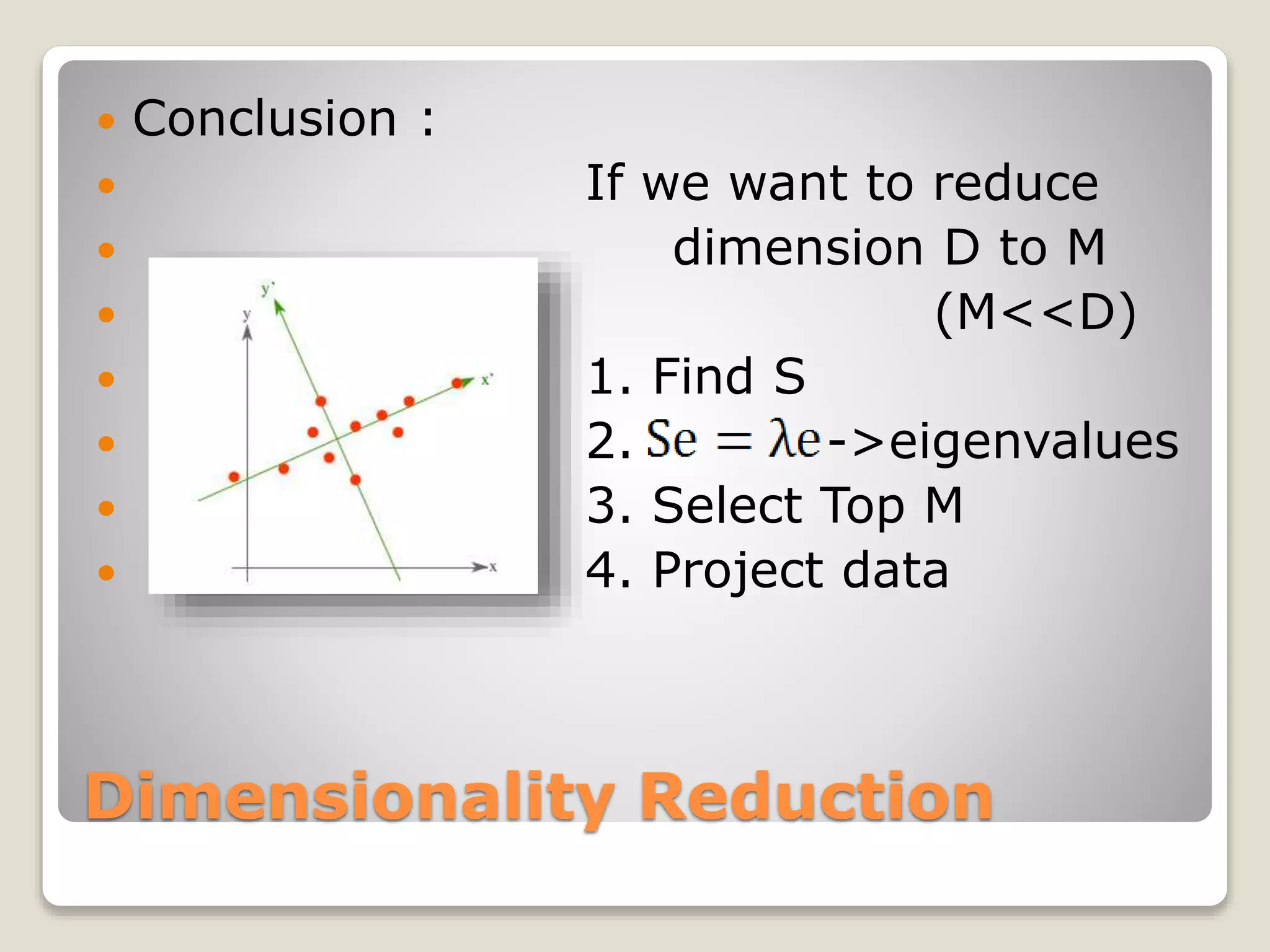
22. Dimensionality Reduction
 We want to proof :
◦ Axes of the data are independent.
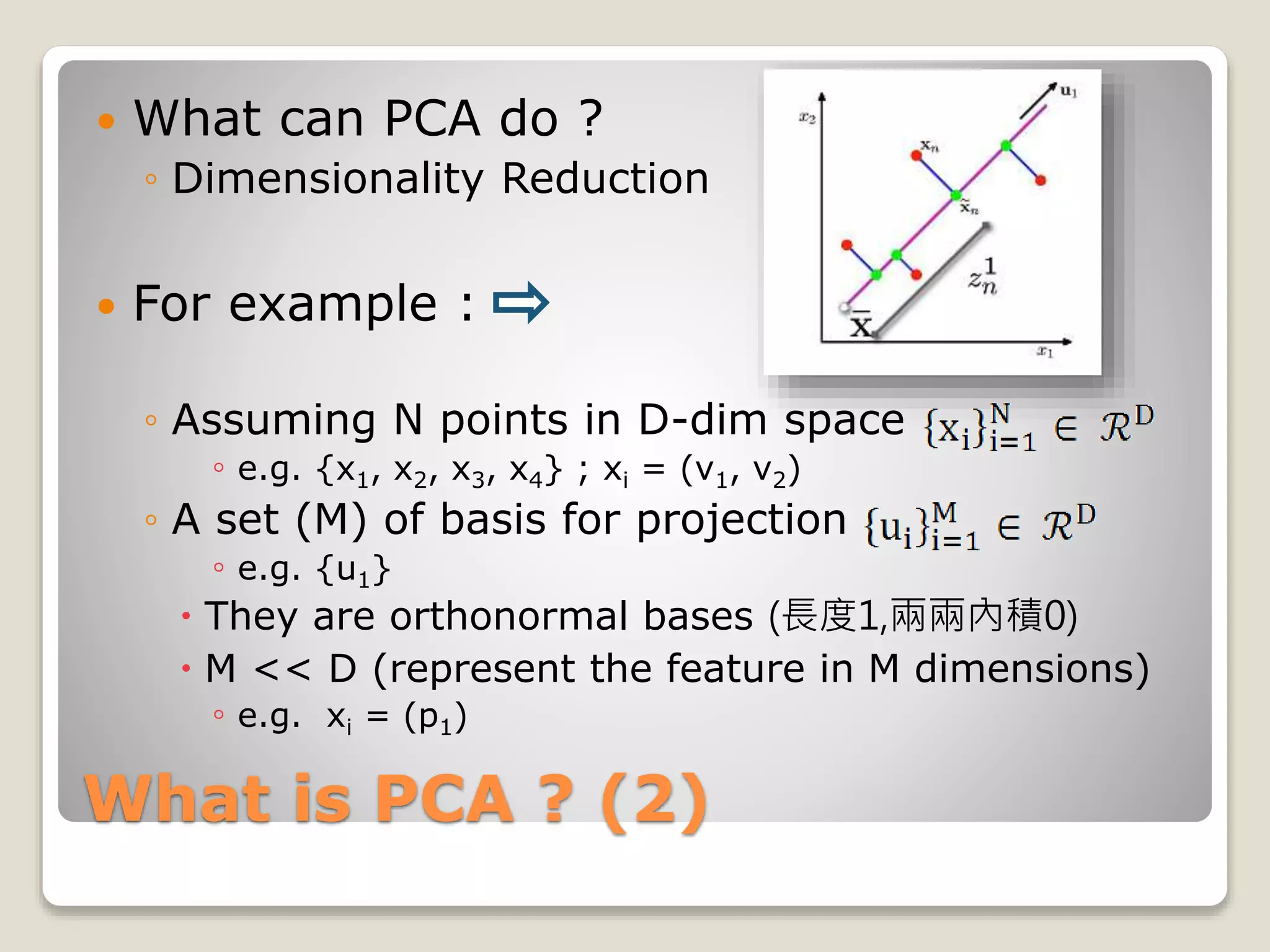
 Consider N m-dim vectors
◦ {x1, x2, … ,xn}
◦ Let X=[x1-m x2-m … xn-m]T m = mean
◦ Let E = [e1 e2 … em]
Se = λe
eigen decomposition Eigen vector {e1,…,em}
Eigen value {λ1,…, λm}

23. Dimensionality Reduction
 SE = [Se1 Se2 … Sem]
 = [λe1 λe2 … λem]

 =
 = ED
 S = EDE-1
E = [e1 e2 … em]

24. Dimensionality Reduction
 We want to know new Covariance Matrix
of projected vectors.
 Let Y = [y1 y2 … yn]T
 E = [e1 e2 … em]
 Y = ETX
 SY

25. Dimensionality Reduction
 SY = D
 1. Covariance of two axes are 0.
 2. represent data↑->covariance of axes↑
 -> λ ↑

26. Dimensionality Reduction
 Conclusion :
 If we want to reduce
 dimension D to M
 (M<<D)
 1. Find S
 2. ->eigenvalues
 3. Select Top M
 4. Project data

27. Agenda
 Theory :
◦ 1. Scenario
◦ 2. What is PCA?
◦ 3. How to minimize Squared-Error ?
◦ 4. Dimensionality Reduction
 Toolkit :
◦ A list of PCA toolkits
◦ Demo

28. Toolkits

29. A List of PCA Toolkits
 C & Java
◦ Fionn Murtagh's Multivariate Data Analysis Software and Resources
◦ http://astro.u-strasbg.fr/~fmurtagh/mda-sw/
 Perl
◦ PDL::PCA
 Matlab
◦ Statistics Toolbox™ : princomp
 Weka
◦ weka.attributeSelection.PrincipalComponents
(http://www.laps.ufpa.br/aldebaro/weka/feature_selection.html )

30. A List of PCA Toolkits
 C & Java
◦ Fionn Murtagh's Multivariate Data Analysis Software and Resources
◦ http://astro.u-strasbg.fr/~fmurtagh/mda-sw/
C :
Download: pca.c
Compile: cc pca.c -lm -o pcac
Run: ./pcac spectr.dat 36 8 R > pcaout.c.txt
Java :
Download: JAMA, PCAcorr.java
Compile: javac –classpath Jama-1.0.2.jar PCAcorr.java
Run: java PCAcorr iris.dat > pcaout.java.txt