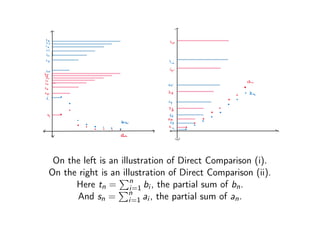
The document summarizes two comparison tests that can be used to determine if an infinite series converges or diverges:
1) The Direct Comparison Test states that if a series with positive terms an is bounded above by a convergent series bn, then an converges. If an is bounded below by a divergent series bn, then an diverges.
2) The Limit Comparison Test states that if the limit of the ratio of the terms of two series is nonzero and finite, then either both series converge or both diverge.
Several examples are provided to illustrate the application of these tests.