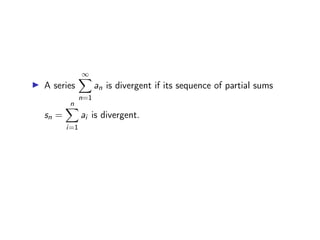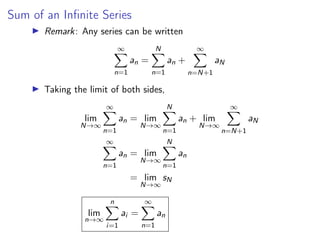
The document provides an outline and overview of topics related to infinite series, including definitions of infinite series and their convergence tests. Some key points: - An infinite series is the sum of the terms of an infinite sequence. - The nth partial sum is used to test for convergence of an infinite series. - Geometric series converge when the common ratio r is between -1 and 1. - The harmonic series, with terms 1/n, is proven to diverge as its partial sums grow without bound.

1. Chapter 11: Sequences, Series, and Power Series
Section 11.2: Series
Alea Wittig
SUNY Albany

2. Outline
Infinite Series
Sum of a Geometric Series
Divergent Series
Test for Divergence
Properties of Convergent Series

3. Infinite Series

4. ▶ Zenos Paradox. If the distance between the person and the
wall is 1 then intuitively we know
1
2
+
1
4
+
1
8
+
1
16
+ . . . +
1
2n
+ . . . = 1
▶ We can write out π as
π = 3.14159 26535 89793 . . .
π = 3 +
1
10
+
4
102
+
1
103
+
5
104
+ . . .
▶ Though we can’t literally add an infinite number of terms, the
more we add, the closer we get to the actual value of π.

5. Infinite Series
▶ An infinite series (or just a series) is the sum
a1 + a2 + . . . + an + . . . =
∞
X
n=1
an =
X
an
of an infinite sequence {an}∞
n=1.

6. Sum of an Infinite Series - Zeno’s Paradox
▶ Consider the example given in Zeno’s paradox.
▶ We know that
∞
X
n=1
1
2n
= 1
intuitively. But how do we prove it mathematically?
▶ Let sn =
n
X
i=1
1
2i
=
1
2
+
1
4
+
1
8
+ . . . +
1
2n−1
+
1
2n
▶ this is called the nth
partial sum of the series
∞
X
n=1
1
2n

7. Sum of an Infinite Series - Zeno’s Paradox
2sn = 2
n
X
i=1
1
2i
=
2
2
+
2
22
+
2
23
+ . . . +
2
2n−1
+
2
2n
= 1 +
1
2
+
1
4
+ . . . +
1
2n−1
= 1 +
n−1
X
i=1
1
2i
= 1 +
n
X
i=1
1
2i
−
1
2n
=⇒
2sn = 1 + sn −
1
2n
sn = 1 −
1
2n
Now,
lim
n→∞
sn = lim
n→∞
1 −
1
2n
= 1 ✓

8. Sum of an Infinite Series
We take this general approach as follows:
▶ Given a series
∞
X
n=1
an = a1 + a2 + . . . + an + . . .
let sn denote its nth partial sum:
sn =
n
X
i=1
ai = a1 + a2 + . . . + an−1 + an

9. Sum of an Infinite Series
▶ If the sequence of terms an is convergent and the sequence of
partial sums is convergent, ie,
lim
n→∞
n
X
i=1
an = lim
n→∞
sn = s
exists as a real number, then the series
∞
X
n=1
an is convergent
and we write
∞
X
n=1
an = s
▶ The number s is called the sum of the series.
▶ If the sequence sn is divergent then the series is called
divergent.

10. Sum of an Infinite Series
▶ Remark: Any series can be written
∞
X
n=1
an =
N
X
n=1
an +
∞
X
n=N+1
aN
▶ Taking the limit of both sides,
lim
N→∞
∞
X
n=1
an = lim
N→∞
N
X
n=1
an + lim
N→∞
∞
X
n=N+1
aN
∞
X
n=1
an = lim
N→∞
N
X
n=1
an
= lim
N→∞
sN
lim
n→∞
n
X
i=1
ai =
∞
X
n=1
an

11. Example 1
Suppose we know that the nth partial sum of the series
∞
X
n=1
an is
sn =
2n
3n + 5
To determine if the series
∞
X
n=1
an converges, we take the limit of sn.
lim
n→∞
sn = lim
n→∞
2n
3n + 5
= lim
n→∞
2n
n
3n
n + 5
n
= lim
n→∞
2
3 + 5
n
=
2
3
So the series
P∞
n=1 an converges to 2
3 , ie,
P∞
n=1 an = 2
3 .

12. Example 2
1/2
Suppose we want to determine whether the following series
converges, and find the sum if possible.
∞
X
n=1
1
n(n + 1)
▶ This time we must find a formula for the partial sum:
sn =
n
X
i=1
1
i(i + 1)
▶ We can write 1
i(i+1) = i+1−i
i(i+1) = i+1
i(i+1) − i
i(i+1) = 1
i − 1
i+1 so
sn =
n
X
i=1
1
i
−
1
i + 1

13. Example 2
2/2
sn =
n
X
i=1
1
i
−
1
i + 1
=
1
1
−
1
2
+
1
2
−
1
3
+
1
3
−
1
4
+ . . . +
1
n
−
1
n + 1
= 1 −
1
n + 1
▶ A sum which has terms that cancel in pairs is called
telescoping.
▶ The sum collapses into two terms like a pirates collapsing
telescope.
lim
n→∞
sn = lim
n→∞
1 −
1
n + 1
= 1 =⇒
∞
X
n=1
1
n(n + 1)
= 1

14. Sum of a Geometric Series

15. Geometric Series
▶ A geometric series is a series of the form
∞
X
n=1
arn−1
= a + ar + ar2
+ . . . + arn−1
+ . . . (a ̸= 0)
eg, The series in Zenos paradox is geometric with a = r = 1
2
eg,
∞
X
n=1
7n
5n+1
is a geometric series with a = 1
5 and r = 7
5 because
we can write
7n
5n+1
=
7n
5 · 5n
=
1
5
·
7n
5n
=
1
5
7
5
n

16. ▶ Now let’s determine for which values of r the geometric series
∞
X
n=1
arn−1
converges.
▶ If r = 1 then
sn =
n
X
i=1
a = a + a + a + . . . + a = na
=⇒ lim
n→∞
sn = lim
n→∞
na
= a lim
n→∞
n =
(
∞ if a 0
−∞ if a 0
▶ Note: infinite series of a nonzero constant is always divergent
∞
X
n=1
a = a + a + a + . . . + a + . . . → ±∞

17. ▶ If r ̸= 1 we have
sn = a + ar + ar2
+ . . . + arn−2
+ arn−1
rsn = ar + ar2
+ ar3
+ . . . + arn−1
| {z }
sn−a
+arn
= sn − a + arn
=⇒
rsn − sn = arn
− a
sn(r − 1) = a(rn
− 1) =⇒
sn =
a(1 − rn)
1 − r

18. ▶ Now taking the limit of sn we have
lim
n→∞
sn = lim
n→∞
a(1 − rn)
1 − r
=
a
1 − r
lim
n→∞
(1 − rn
)
=
a
1 − r
−
a
1 − r
lim
n→∞
rn
▶ Recall from 11.1 that {rn} is convergent if −1 r ≤ 1 and
divergent for all other values of r.
▶ In particular
lim
n→∞
rn
=





0 if − 1 r 1
1 if r = 1
Diverges for all other values of r

19. Geometric Series Convergence
▶ So for −1 r 1,
lim
n→∞
sn =
a
1 − r
−
a
1 − r
lim
n→∞
rn
=
a
1 − r
∞
X
n=1
arn−1
=
a
1 − r
if |r| 1 and divergent for all other values of r

20. Example 3
5 −
10
3
+
20
9
−
40
27
+ . . .
▶ To determine if the series converges and find its sum if
possible, we notice it is geometric and write it in the form
P∞
n=1 arn−1.
5 −
10
3
+
20
9
−
40
27
+ . . . = 5
1 −
2
3
+
4
9
−
8
27
− . . .
= 5
∞
X
n=1
−
2
3
n−1
=
∞
X
n=1
5
−
2
3
n−1
▶ a = 5, r = −2
3 and since |r| = 2
3 1, the series converges to
s =
5
1 + 2
3
=
5
5
3
= 3

21. Example 4
∞
X
n=1
22n
31−n
∞
X
n=1
22n
31−n
=
X
n=1
(22
)n 3
3n
=
X
n=1
3
4
3
n
=
X
n=1
3
4
3
4
3
n−1
=
X
n=1
4
4
3
n−1
So a = 4 and r = 4
3 1 so this series diverges.

22. Example 5
1/2
▶ A rational number q is a number that can be written in the
form q = m
n where m and n are integers and n ̸= 0.
▶ Any number with a repeated decimal representation is a
rational number because it can be written in this form.
▶ As an example, let’s write the number
2.34 = 2.3434343434 . . . as a ratio of integers.
2.34 = 2 +
3
10
+
4
100
+ +
3
1, 000
+
4
10, 000
+
3
105
+
4
106
+ . . .
= 2 + 3
1
10
+
1
1, 000
+
1
105
+ . . .
+ 4
1
100
+
1
10, 000
+
1
106
+ . . .
= 2 + 3
1
101
+
1
103
+
1
105
+ . . .
+ 4
1
102
+
1
104
+
1
106
+ . . .
= 2 + 3
∞
X
n=1
1
102n−1
+ 4
∞
X
n=1
1
102n

23. Example 5
2/2
2 + 3
∞
X
n=1
1
102n−1
+ 4
∞
X
n=1
1
102n
= 2 + 3
∞
X
n=1
10
1
102
n
+ 4
∞
X
n=1
1
102
n
= 2 + 3
∞
X
n=1
10
1
102
1
102
n−1
+ 4
∞
X
n=1
1
102
1
102
n−1
= 2 +
∞
X
n=1
3
10
1
102
n−1
+
∞
X
n=1
4
102
1
102
n−1
= 2 +
3
10
1 − 1
102
+
4
102
1 − 1
102
= 2 +
30
99
+
4
99
=
2(99) + 30 + 4
99
=
232
99

24. Example 6
1/2
Find the sum of the series
∞
X
n=0
xn
where |x| 1
∞
X
n=0
xn
= x0
+ x1
+ x2
+ x3
+ . . .
= 1 + x + x2
+ x3
+ . . .
= 1 +
∞
X
n=1
xn
= 1 +
∞
X
n=1
x · xn−1

25. Example 6
2/2
1 +
∞
X
n=1
x · xn−1
| {z }
a=x, r=x
= 1 +
x
1 − x
| {z }
a
1−r
=
1 − x
1 − x
+
x
1 − x
=
1
1 − x
▶ This example demonstrates that on the interval (−1, 1), the
function f (x) =
1
1 − x
has the power series representation
f (x) =
∞
X
n=0
xn
.

26. Divergent Series

27. ▶ A series
∞
X
n=1
an is divergent if its sequence of partial sums
sn =
n
X
i=1
ai is divergent.

28. Harmonic Series
Show that the harmonic series
∞
X
n=1
1
n
is divergent.
▶ The harmonic series is an important series whose name derives
from the concept of overtones in music.
▶ It will be difficult to find a simple formula for the nth partial
sum.
▶ Instead we will show that the 2nth partial sum s2n , is divergent.
▶ Writing out the first few terms of s2n we will observe that
s2n 1 + n
2 for each n.

29. Harmonic Series
s21 = s2 = 1 +
1
2
(n=1)
s22 = s4 = s2 +
1
3
+
1
4
(n=2)
s2 +
1
4
+
1
4
= s2 +
1
2
= 1 +
2
2

30. Harmonic Series
s23 = s8 = s4 +
1
5
+
1
6
+
1
7
+
1
8
(n=3)
s4 +
1
8
+
1
8
+
1
8
+
1
8
= s4 +
4
8
1 +
2
2
+
4
8
since s4 1 +
2
2
= 1 +
3
2

31. Harmonic Series
s24 = s16 = s8 +
1
9
+
1
10
+
1
11
+ . . . +
1
16
(n=4)
s8 +
1
16
+
1
16
+
1
16
+ . . . +
1
16
= s8 +
8
16
1 +
4
2
since s8 1 +
3
2
▶ In general s2n 1 + n
2 for each n.
lim
n→∞
s2n 1 + lim
n→∞
n
2
= ∞
▶ Since s2n diverges, that means sn must diverge as well.
▶ Thus the harmonic series diverges.

32. Divergent Series
▶ Finding a formula for the nth partial sum of a series can be
quite challenging.
▶ In many cases, taking the limit of the partial sum won’t be the
most efficient method to determine whether a series converges
or diverges.
▶ In order for the series
∞
X
n=1
an to converge, it’s sequence of
terms an must converge as well.
▶ In fact, the next theorem tells us something even stronger.

33. Test for Divergence

34. Test for Divergence
Theorem 6: If the series
∞
X
n=1
an is convergent, then lim
n→∞
an = 0.
▶ WARNING: The converse of this theorem is false.
▶ ie, lim
n→∞
an = 0 does not imply that the series
∞
X
n=1
an converges.
▶ The harmonic series is an example of when the converse fails
since limn→∞
1
n = 0 but
P 1
n diverges.
▶ However, the contrapositive statement of the theorem, which
is equivalent to the theorem, is called the Test for Divergence
and will be very useful.
Test for Divergence : lim
n→∞
an ̸= 0 =⇒
∞
X
n=1
an is divergent.

35. Example 7
1/2
Show that the series
∞
X
n=1
n2
5n2 + 4
diverges.

36. Example 7
2/2
lim
n→∞
n2
5n2 + 4
= lim
n→∞
1
5 + 4
n2
=
1
5
̸= 0
=⇒
∞
X
n=1
n2
5n2 + 4
diverges by the test for divergence

37. Properties of Convergent Series

38. Theorem: If
P
an =
P
bn are convergent series, then so are the
series
P
can,
P
an +
P
bn, and
P
an −
P
bn
(i)
P
can = c
P
an
(ii)
P
(an + bn) =
P
an +
P
bn
(iii)
P
(an − bn) =
P
an −
P
bn

39. Example 8
1/2
Find the sum of the series
∞
X
n=1
3
n(n + 1)
+
1
2n

40. Example 8
2/2
▶ From example 1 we have,
∞
X
n=1
1
n(n + 1)
= 1
▶ And from the geometric series theorem,
∞
X
n=1
1
2n
= 1
∞
X
n=1
3
n(n + 1)
+
1
2n
= 3
∞
X
n=1
1
n(n + 1)
+
∞
X
n=1
1
2n
= 3 + 1
= 4