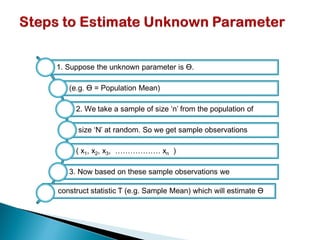
The document provides an overview of estimation techniques in statistics, focusing on point and interval estimation. Point estimation gives a single value to estimate a population parameter based on a sample, while interval estimation uses a range to indicate where the parameter may lie with a certain confidence level. It also includes examples and formulae for calculating sample size and confidence intervals.

1. CPT Section D Quantitative Aptitude Chapter 15
Prof. Bharat Koshti

2. Theory of estimation :
It deals with estimating unknown values of the Population
parameters.
There are two types of estimation techniques :
1.Point Estimation
2. Interval Estimation
1. Point Estimation: When a single value is proposed to
estimate, it is called as Point estimation.

3. 1. Suppose the unknown parameter is ϴ.
(e.g. ϴ = Population Mean)
2. We take a sample of size ‘n’ from the population of
size ‘N’ at random. So we get sample observations
( x1, x2, x3, ……………… xn )
3. Now based on these sample observations we
construct statistic T (e.g. Sample Mean) which will estimate ϴ

4. T is a single value obtained from the sample &
is known as point estimator.
The point estimator of Population Mean(μ),
Population Standard Deviation(σ) & Population
Proportion(P) are the corresponding sample
Mean(x̅),Sample Standard Deviation(s) &
Sample Proportion(p).

5. Ex1. Consider sample observations
14,15,6,17,28 from population of 100 units. Find
an estimate of population mean.
Estimate of μ is given by X̅
X̅ = (14+15+6+17+28)/5
X̅ = 16
Hence, estimate of μ is 16.

6. Ex2. A random sample of 150 articles taken from a large batch of
articles contains 15 defective articles. Find an estimate of the
proportion of defective articles in the entire batch? Also find its
Standard error(SE).
Estimate of p = P i.e.
Sample Proportion estimates Population Proportion.
p = 15/150 = 0.10
SE = SQRT{p(1-p)/n} = SQRT{ 0.1(1-0.1)/150} = 0.0245
(since N is very large fpc is ignored)

7. Interval estimation specifies two values that contain unknown
parameter ϴ on the basis of random sample drawn from the
population. Thus interval (T1,T2) is likely to contain parameter
ϴ. T1 is called Upper Confidence Limit(UCL) & T2 is called
Lower Confidence Limit(LCL).
The probability that the confidence interval contains the
parameter is called confidence co-efficient and it is denoted as
(1-α)%.
If α is 0.05 then (1- α)% would be (1-0.05)% = 95%. It shows the
amount of confidence.
If α is 0.01 then (1- α)% would be (1-0.01)% = 99%.

8. Assuming we have drawn random sample from the
Normal Population with mean μ and standard deviation
σ. Following Z values are important for various
confidence Level.
Confidence Level (α) 99% 95% 90%
Confidence Co-efficient(Z) 2.58 1.96 1.64

9. From a certain college of 3000 students a sample of 200
students is taken and their weights are recorded.
The average weight of 200 students was found to be 65kg
with the standard deviation of 10kg.
Construct a 99% confidence interval for the population
mean.
99 % confidence interval
= ( x̅ - 2.58 σ / √n̅, x̅ + 2.58 σ / √n )
= ( 65 -2.58X 10/ √200 , 65 +2.58X 10/ √200)
= (63.17 , 66.82)

10. A manufacturing industry which manufactures electronics
IC’s. From the daily production process of 10000 IC’s a
sample of 150 IC’s is taken at random and 5% IC’s were
found to be defective.
Estimate the no. of defective IC’s that can be produced in
daily production process. Use 95% level of significance.
95 % confidence interval
= (p - √pq/n x sqrt(N-n/N-1), p + √pq/n x sqrt (N-n/N-1))
Here p = 0.05, N = 10,000, n = 200 q = 1-p = 0.95
= ( 0.0323,0.0676)
Hence (0.0323x10000, 0.0676x10000) = (323, 676)

11. FORMULA: Sample size = n = (σ Z / E)2
Where,
E = Admissible error while estimating the parameter μ.
σ = SD & Z = Table Value for Normal Distribution.
Example: Given σ = 10 , what should be size of the sample in
order to be 99% confident that error estimate of mean would
not exceed 2?
Here E = 2, σ = 10 Z = 2.58
n = (σ Z / E)2
= (10x2.58 /2)2
= 166

12. MCQ’s

13. (a) Only one
(b) Two
(c) Three
(d) Many
Answer: D

14. MCQ.2: The most commonly used
confidence interval is
(a) 95 percent
(b) 90 percent
(c) 94 percent
(d) 98 percent
Answer: A

15. MCQ.3:It is known that the population standard
deviation in waiting of getting PAN card is 13 days.
How large a sample should be taken to be 99%
confident that the waiting time is within 8 days of
true average? (use z = 2.58)
(a) 18 days
(b) 13 days
(c) 19 days
(d) 14 days
Answer: A

16. MCQ:4
• It is known that x̅ = 55 for sample of 64
units & SE(x̅)=1.5, calculate confidence
interval at 99%.(use z = 2.58 )
(a) (51.13,58.87)
(b) (51.13,51.87)
(c) ( 51.87,58.13)
(d) (51.31,51.78)
Answer: A

17. MCQ.5:The estimate of the parameter is
stated as an interval with a specified
degree of
(a) confidence
(b) interval
(c ) class
(d ) None
Answer: A

18. MCQ.6: The standard deviation in the
sampling is called
(a) Standard error
(b) Absolute error
(c ) Relative error
(d ) None
Answer: A

19. MCQ.7: The standard deviation in the
sampling is called
(a) Standard error
(b) Absolute error
(c ) Relative error
(d ) None
Answer: A

20. MCQ.8:The ratio of no. of elements
possessing a characteristic to the total
no. of elements in a sample is known as -
(a) Sample Proportion
(b) Population Proportion
(c ) Sample size
(d ) None
Answer: A

21. 9. The Confidence limits are the upper &
lower limits of the
(a) Point estimate
(b) Interval estimate
(c ) Confidence interval
(d ) None
Answer: C

22. MCQ.10: Different types of estimates
about a population parameter are -
(a) Two
(b) Three
(c ) Four
(d ) Five
Answer: A

23. Thank you