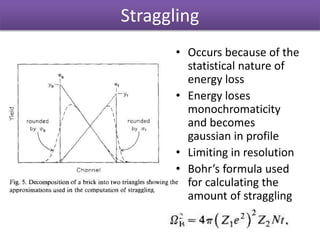
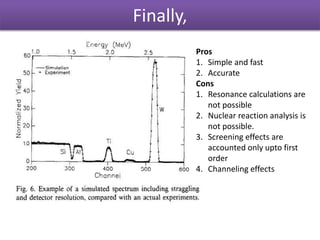
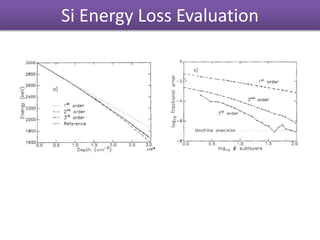
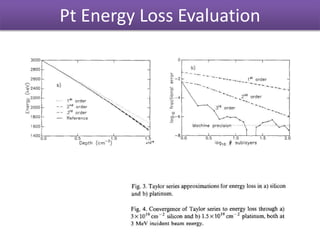
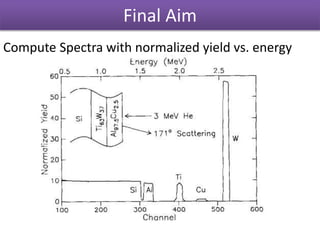
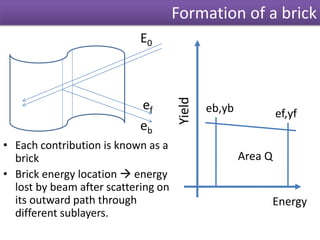
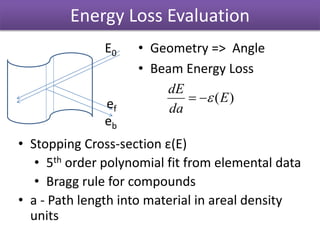
The document discusses Rutherford backscattering (RBS) modeling algorithms, focusing on efficient computation methods to analyze RBS spectra using assumptions about sample composition and energy loss. It outlines methodologies for energy loss evaluation, spectrum building, and the impact of various factors like scattering cross-sections and statistical nature of energy loss. The conclusions highlight the advantages of the proposed algorithms, such as speed and accuracy, as well as limitations regarding complex nuclear reaction analysis.

1. Rutherford Backscattering Modeling
Algorithms
Shuvan Prashant
PC5209 Coursework
Nuclear Instruments and Methods in Physics Research B9 (1985) 344-351

2. Motivation
• RBS analysis algorithms though accurate but
computationally intensive
• Takes a lot of time on small computers
• Rapid simulation with good assumptions can fit
the RBS spectra with reasonable accuracy
Computers are useless. They can only give you answers.
Pablo Picasso

3. Final Aim
Compute Spectra with normalized yield vs. energy

4. Assumptions
• Sample  stack of sublayers
• Sublayer  uniform composition and fixed
energy loss function(E dependent only)
• Sublayer should not be too thick
• Elastic Scattering
• Screening for low energies can be incorporated
• Detector resolution  Gaussian convolution
• Straggling  intensive but possible

5. Formation of a brick
• Each contribution is known as a
brick
• Brick energy location  energy
lost by beam after scattering on
its outward path through
different sublayers.
Yield
Energy
Area Q
eb,yb ef,yf
ef
eb
E0

6. Energy Loss Evaluation
• Geometry => Angle
• Beam Energy Loss
ef
eb
E0
)(E
da
dE

• Stopping Cross-section ε(E)
• 5th order polynomial fit from elemental data
• Bragg rule for compounds
• a - Path length into material in areal density
units

7. To calculate E(Ntsecθ)
Expand using Taylor Series
...
6
1
2
1
)0()(
0
3
3
3
0
2
2
2
0

da
Ed
a
da
Ed
a
da
dE
aEaE
Surface Approximation( Upto first order)
...)'''(')( 223
6
12
2
1
0   aaaEaE
Using the definition of ε(E) and evaluating
higher differential terms ε’ and ε’’,
)(E
da
dE


8. Energy Location
• Assuming elastic scattering,
• Eafter prop to Ebefore
• Evaluate Kinematic factors for different
elements
2
1
2
22
1
cossin1
M
M
whereK 










 



9. Building Spectrum
• Superpose contributions from each isotope in
sublayer in the sample
• Spectrum Calculation involves
– Energy Loss evaluation in each sublayer
– Final Interpolation of the spectrum
• Shape of the brick Trapezoidal bricks may
have kinks if the sublayers are thick
• Area not accurate
• How can we solve this ?

10. Solution
• Assume parabolic top profiles
• Rutherford Scattering Cross-section for a small
solid angle



sec
0
))((Area
Nt
daaE
 




22
4
222
21
sin1cos
cossin
coscos
2
)(










where
E
eZZ
E
2
)(generalinnuclidesFor 
 CEE
orderthirdofpolynomialausing
edapproximatisE(a)where)(Area 2-
sec
0
2



Nt
daaEC

11. Height Estimation
)()()]([
)(
)(
cos)]([
)(
EKEKEwhere
E
E
E
Ex
y
AAAi
layers out
in
Ai
iAA






 
Screening Effects can be accounted
keVwhere
aE
p
EE R 4/3
21ZZ0.049
a
p
)1)(()( 


For high Z elements and 2MeV beam, the deviation of cross-section
is about 2% .

12. Virtual MCA
• Using values of eb, ef, yb, yf and Q , evaluate
the coefficients A, B and C
• Virtual MCA evaluates the expression at
boundary points of the channels and
substracts to get the yield per channel.
32
2
32
CeBeAedeheightYield
CeBeAheight




13. Computation
• Stage 1
– Calculate energy on inward path and Rutherford
Integrals  prop to # of sublayers
• Stage 2
– Outward energy loss for each nuclide present at
interface
– Interface.nuclide.depth  # of sublayers
• Stage 3
– Stopping cross-sections

14. Straggling
• Occurs because of the
statistical nature of
energy loss
• Energy loses
monochromaticity
and becomes
gaussian in profile
• Limiting in resolution
• Bohr’s formula used
for calculating the
amount of straggling

15. Finally,
Pros
1. Simple and fast
2. Accurate
Cons
1. Resonance calculations are
not possible
2. Nuclear reaction analysis is
not possible.
3. Screening effects are
accounted only upto first
order
4. Channeling effects

16. Thanks for your attention
• Q & A

17. Si Energy Loss Evaluation

18. Pt Energy Loss Evaluation