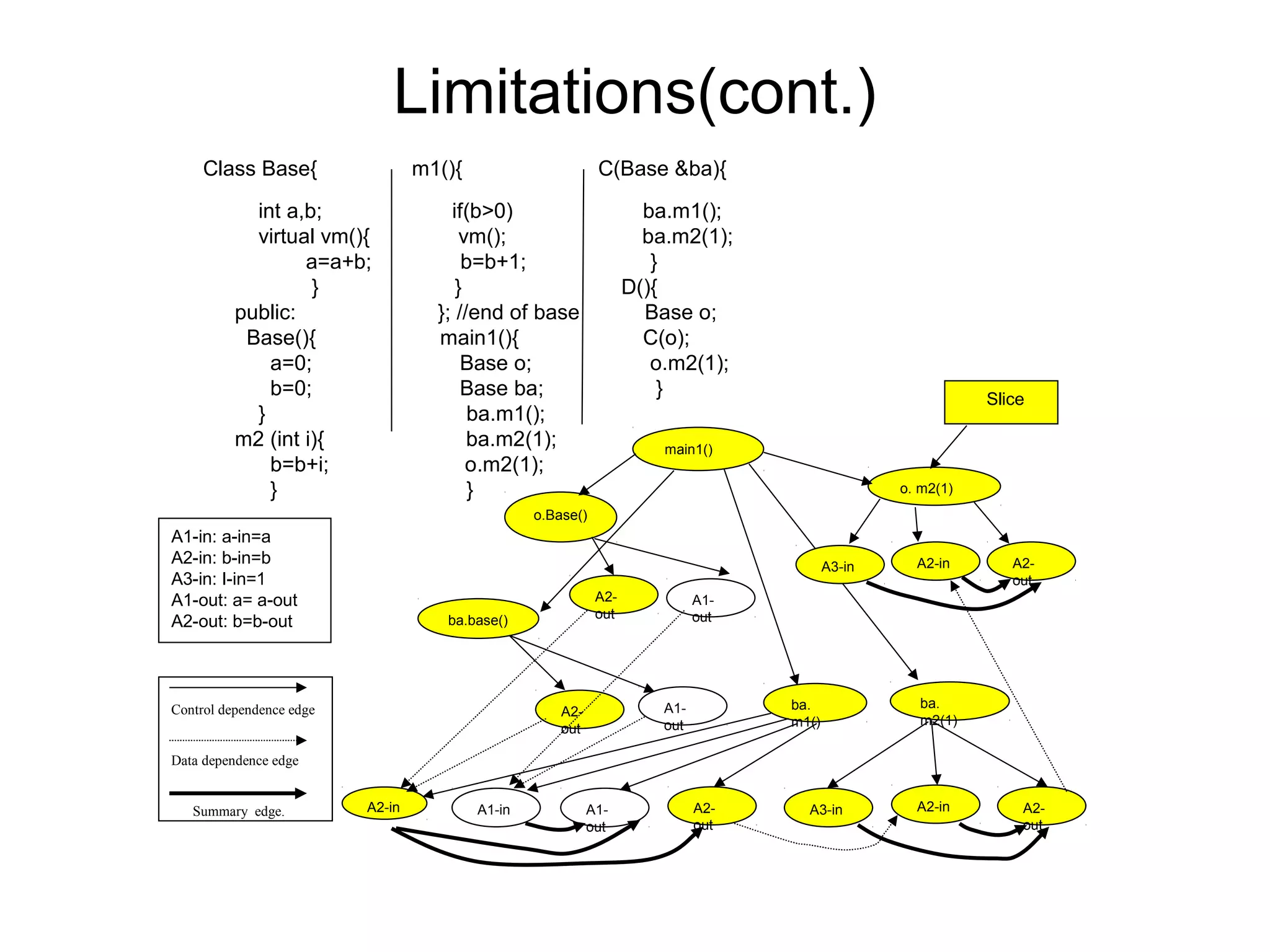
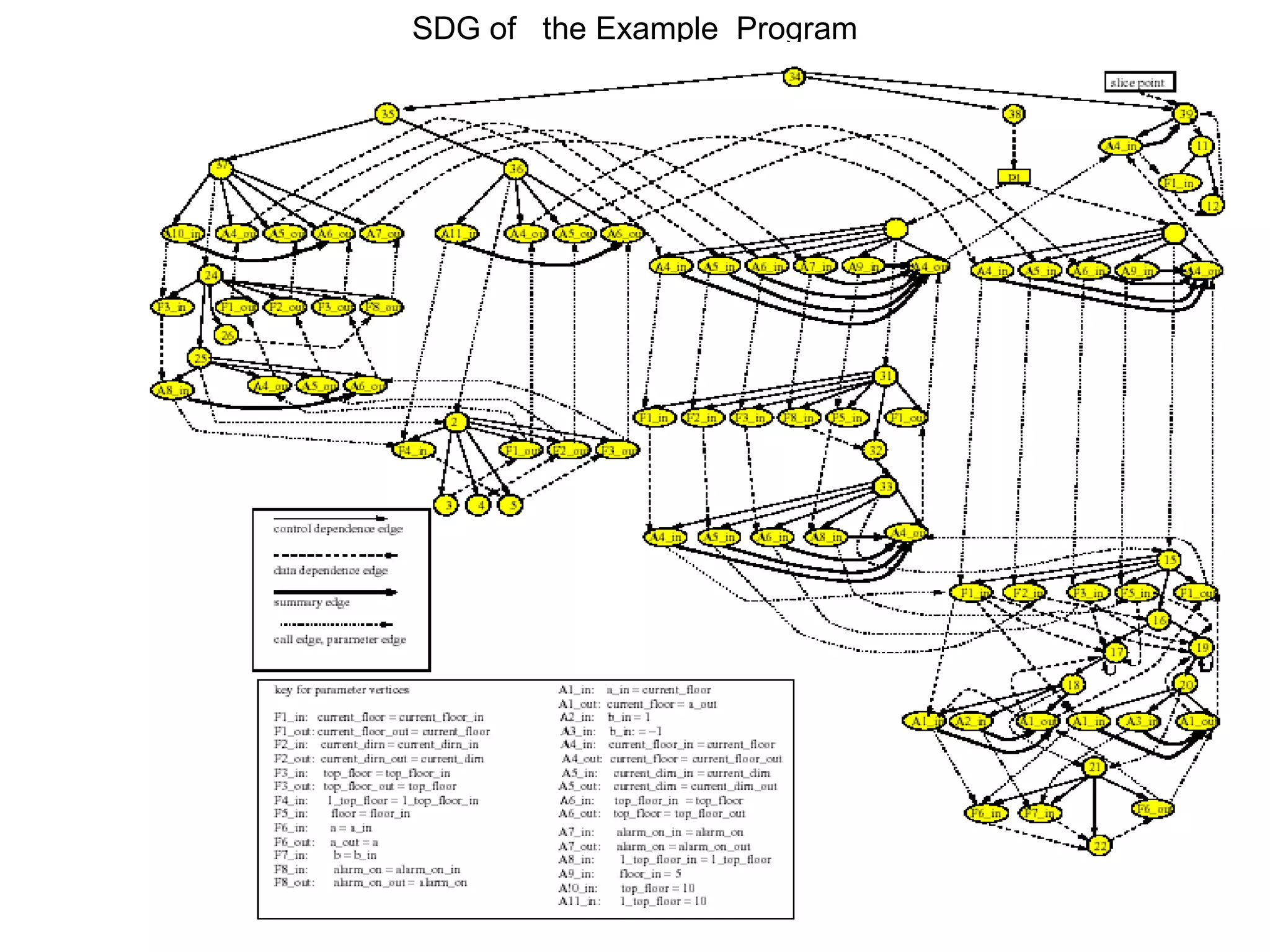
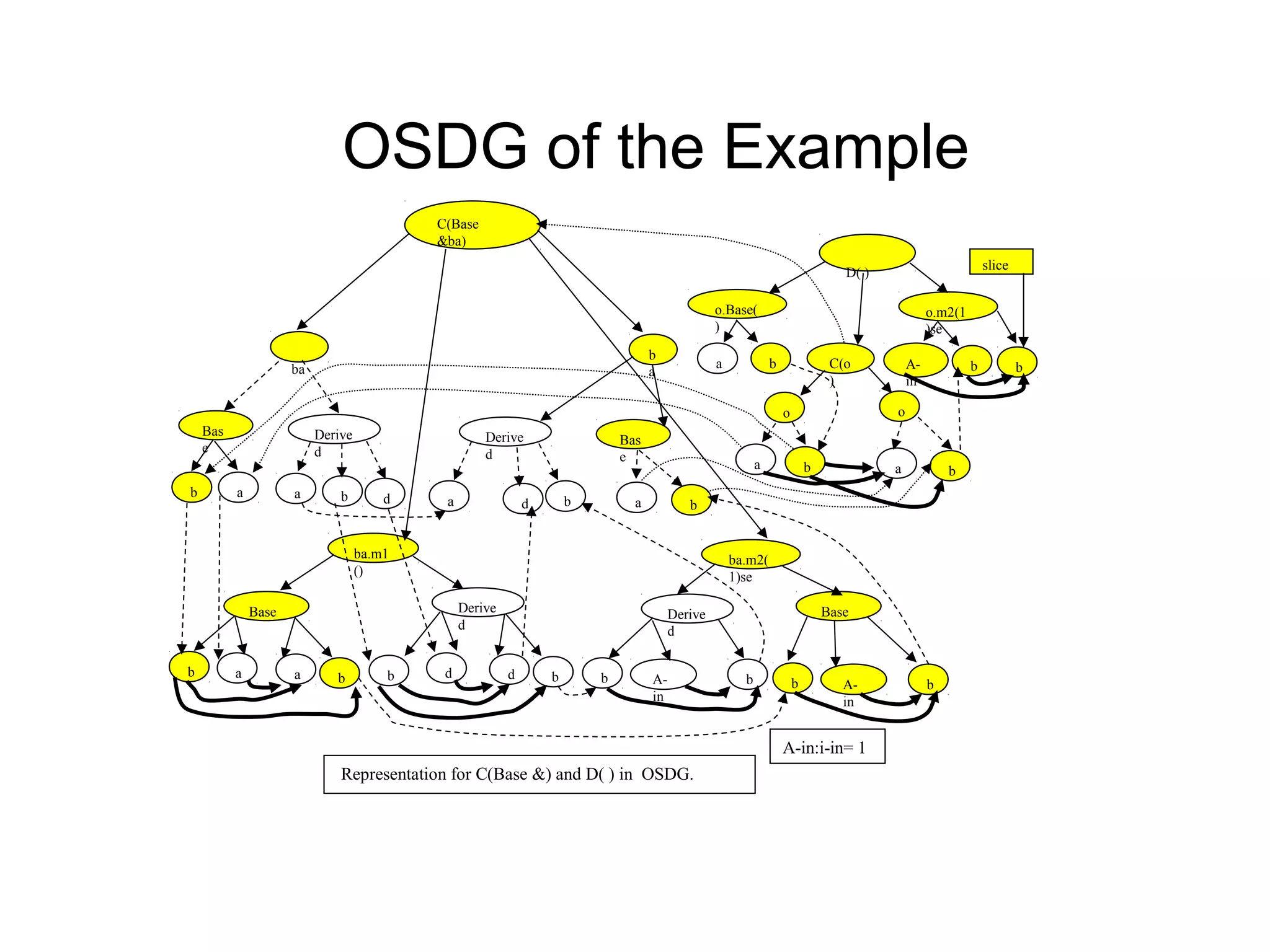
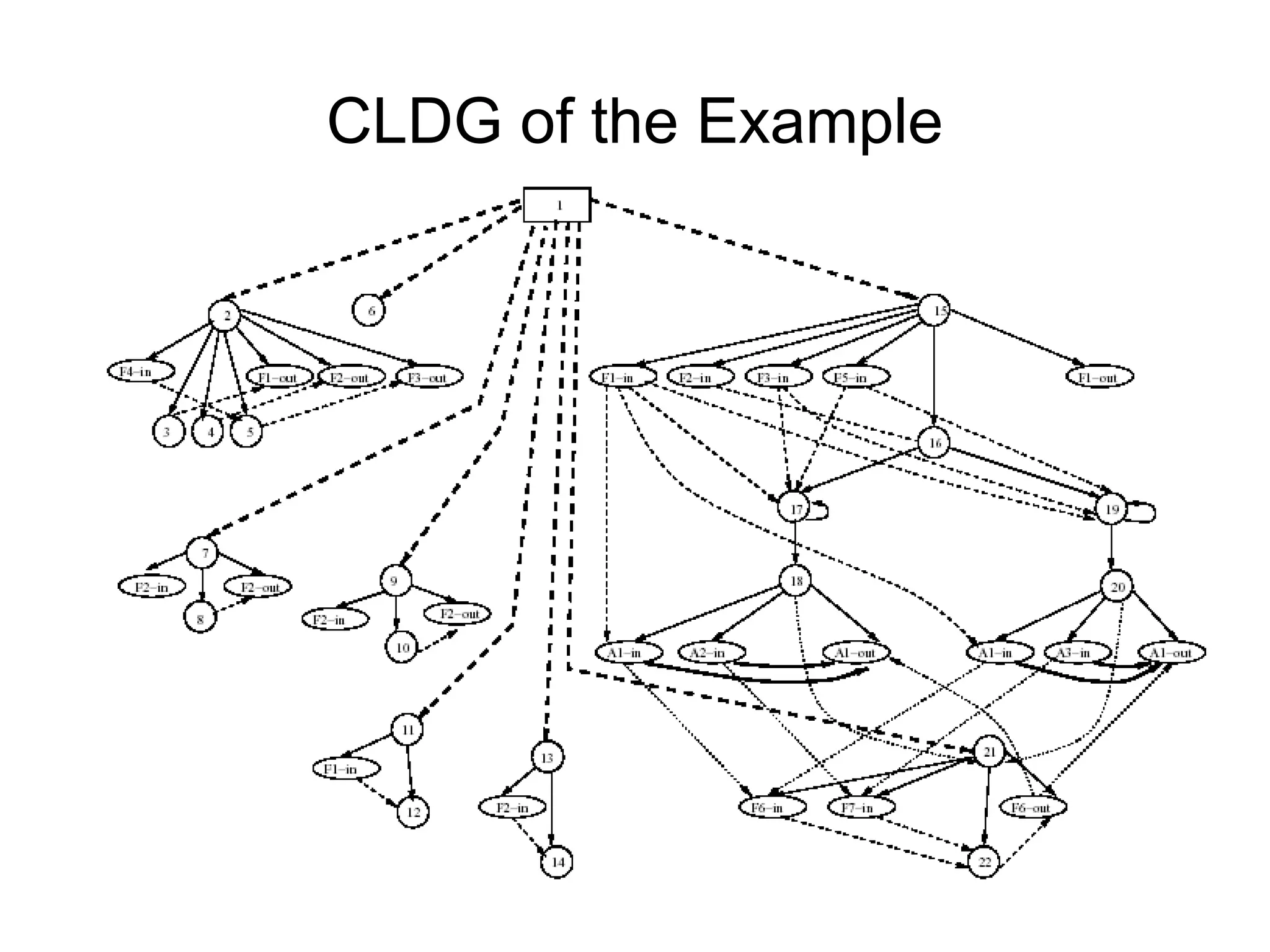
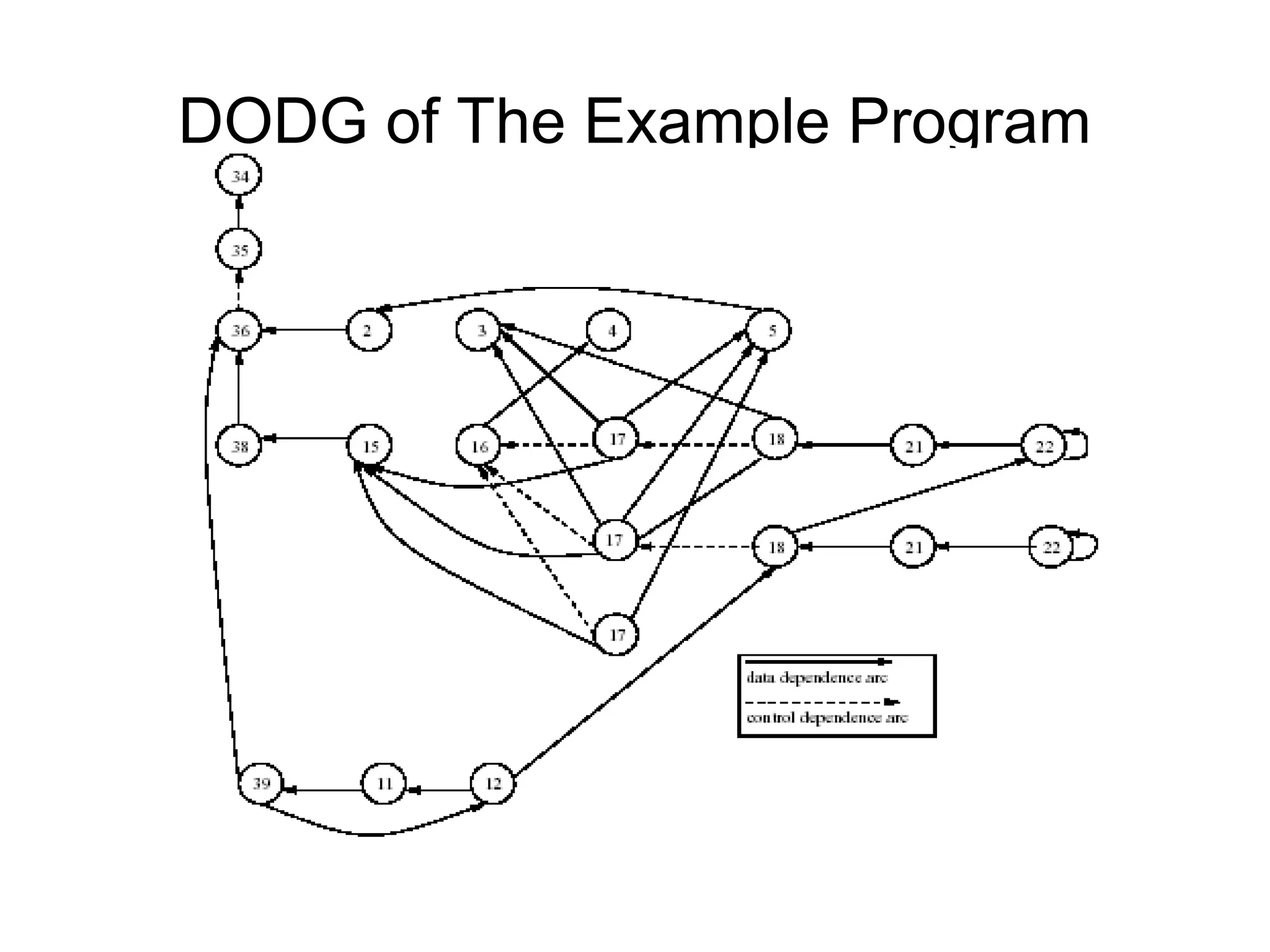
- The document summarizes techniques for slicing object-oriented programs. It discusses static and dynamic slicing, and limitations of previous approaches. - It proposes a new intermediate representation called the Object-Oriented System Dependence Graph (OSDG) to more precisely capture dependencies in object-oriented programs. The OSDG explicitly represents data members of objects. - An edge-marking algorithm is presented for efficiently performing dynamic slicing of object-oriented programs using the OSDG. This avoids recomputing the entire slice after each statement.

1. Slicing of Object-Oriented
Programs
Durga Prasad Mohapatra
Roll No- 02CS9701
Supervisors: Dr. Rajib Mall
Dr. Rajeev Kumar

2. Outline of the Seminar
• Introduction
• Interprocedural slicing
• Static Slicing of OOP
• Static Slicing of Concurrent OOP
• Dynamic Slicing of OOP
• Motivation for Research
• Objective of Research
• Work Done/ Work to be done
• publications

3. Program Slicing
• Slice of a program w.r.t. program point p and
variable x:
- All statements and predicates that might
affect the value of x at point p.
• <p, x> known as slicing criterion.

4. Example
1 main( )
2 {
3 int i, sum;
4 sum = 0;
5 i = 1;
6 while(i <= 10)
7 {
8 Sum = sum + 1;
9 ++ i;
10 }
11 printf(“%d”, sum);
12 printf(“%d”, i);
13 }
An Example Program & its slice w.r.t. <12, i>

5. Types of Slice
• Static Slice: Statements that may affect value of
a variable at a program point for all possible
executions.
• Dynamic Slice: Statements that actually affect
value of a variable at a program point for that
particular execution.
• Backward Slice: Statements that might have
affected the variable at a program point.
• Forward Slice: Statements that might be
affected by the variable at a program point.

6. Applications of Slicing
• Debugging
• Program understanding
• Testing
• Software maintenance
• Complexity measurement
• Program integration
• Reverse engineering
• Software reuse

7. Approaches to Slicing
• CFG- based: Data flow equations are solved
• Dependence graph-based:
-PDG is used as intermediate representation
-Slice is computed as a reachability problem
• PDG of an OOP is a directed graph in which
-nodes represent statements and predicates
-edges represent data/control dependence
among the nodes

8. Inter-Procedural Slicing
Horwitz’s Approach
• PDG can not handle programs with multiple
procedures.
• Here the intermediate representation is called as
system dependence graph (SDG).
• SDG is based on procedure dependence graphs
• Same as PDG except that it includes vertices &
edges for call statements, parameter passing
& transitive dependence due to calls.

9. Inter-Procedural Slicing(cont.)
• On calling side, parameter passing is
represented by actual-in & out vertices.
• In called procedure, parameter passing is
represented by formal-in & out vertices.

10. Inter-Procedural slicing (cont.)
• A call edge is added from call site vertex to
corresponding procedure entry vertex.
• A parameter-in edge is added from each actual-
in vertex to corresponding formal-in vertex.
• A parameter-out edge is added from each
formal-out vertex to corresponding actual-out
vertex.
• To find the slice, Horwitz proposed a two-pass
algorithm.

11. Inter-Procedural Slicing (cont.)
• The traversal in pass one starts from desired
vertex & goes backwards along all edges except
parameter-out edges.
• The traversal in pass two starts from all vertices
reached in pass one and goes backwards along
all edges except call & parameter-in edges.
• The slice is the union of 2 sets of vertices.

13. Slicing of OOPs
• Present-day software systems are basically
object-oriented.
• O-O features such as classes, inheritance,
polymorphism need to be considered in slicing.
• Due to presence of polymorphism and dynamic
binding, process of tracing dependencies in
OOPs becomes complex.

14. Static Slicing of OOP
• Larson and Harrold were the first to consider
these O-O features for slicing by extending the
SDG for OOPs.
• They represented each class by a class
dependence grpah (CLDG).
• The CLDG captures the control and data
dependence relationships of a class.
• Each method in a class, is represented by a
procedure dependence graph.

15. Static Slicing of OOP (cont.)
• Each method has a method entry vertex to
represent the entry into the method.
• CLDG contains a class entry vertex that is
connected to the method entry vertex for each
method, by class member edges.
• To represent parameter passing, CLDG creates
formal-in & formal-out vertices.

16. Static Slicing of OOP (cont.)
• CLDG represents method calls by a call vertex.
• It adds actual-in & actual-out vertices at each
call vertex.

17. Example1 class Elevator {
public
2 Elevator(int1_top_floor)
3 {current_floor = 1;
4 current_direction = UP;
5 top_floor = 1_top_floor; }
6 virtual ~Elevator
7 void up( )
8 {current_direction = UP;}
9 void down( )
10 int which_floor( )
11 {current_direction = DOWN;}
12 {return current_floor; }
13 Direction direction( )
14 {return current_direction; }
15 virtual void go(int floor )
16 {if (current_direction = =UP)
17 {while(current_floor != floor) && (current_floor < = top_floor)
18 add(current_floor, 1); }
else
19 {while(current_floor != floor) && (current_floor > 0)
20 add(current_floor, -1); }
}
private:
21 add(int &a, const int &b)
22 { a = a + b; }
protected:
int current_floor;
Direction current_direction
int top_floor; };

18. 23 class AlarmElevator : public Elevator {
public
24 AlarmElevator ( int top_floor)
25 Elevator (top_floor)
26 {alarm_on = 0;}
27 void set_alarm( )
28 {alarm_on = 1;}
29 void reset_alarm( )
30 {alarm_on = 0;}
31 void go (int floor)
32 { if (!alarm_on)
33 Elevator :: go (floor)
};
protected:
int alarm_on;
} ;
34 main( int argc, char **argv) {
Elevator *e_ptr;
35 If (argv[1])
36 e_ptr = new Elevator (10);
else
37 e_ptr = new AlarmElevator (10);
38 e_ptr - > go(5);
39 c_out << “n currently on floor :” << e_ptr -> which_floor ( );
}

19. CLDG of the Example

20. Representing complete programs
• Construct the partial SDG for main()
• Connect the calls in the partial SDG to methods
in the CLDG for each class, by using
- call edges
- parameter-in edges
- parameter-out edges

21. SDG of the Example Program

22. Slicing the complete program
• Use the two-pass algorithm for computing the
static slice of the OOP.
• Shaded vertices in the SDG, are included in the
slice w.r.t. slicing criterion <39,current_floor>.

23. Limitations of Larson’s Approach
• It can not distinguish data members for different
objects instantiated from the same class.
• It fails to consider the fact that in different
method calls, data members used by the
methods might belong to different objects.

24. Limitations (cont.)
• Thus, it creates spurious data dependences.
• So the resulting slice may be imprecise.
• It can not represent an object that is used as a
parameter or data member of another object.

25. Limitations (cont.)
• It is not fit to represent larger programs, because
for a large program this SDG will be too large to
manage & understand.
• It can not handle dynamic slicing of OOPs.

26. Limitations(cont.)
int a,b; if(b>0) ba.m1();
virtual vm(){ vm(); ba.m2(1);
a=a+b; b=b+1; }
} } D(){
public: }; //end of base Base o;
Base(){ main1(){ C(o);
a=0; Base o; o.m2(1);
b=0; Base ba; }
} ba.m1();
m2 (int i){ ba.m2(1);
b=b+i; o.m2(1);
} }
A2-in
main1()
o.Base()
ba.base()
A2-
out
A1-
out
A2-
out
A1-
out
ba.
m1()
A1-in A2-
out
A1-
out
A3-in A2-in A2-
out
ba.
m2(1)
A3-in A2-
out
A2-in
o. m2(1)
Slice
A1-in: a-in=a
A2-in: b-in=b
A3-in: I-in=1
A1-out: a= a-out
A2-out: b=b-out
Class Base{ m1(){ C(Base &ba){
Control dependence edge
Data dependence edge
Summary edge.

27. Limitations (cont.)
• The data dependence edge between o.base() &
ba.m1() is a spurious data dependence edge.
• C(Base &ba) of the example can not be
represented using this approach.

28. Tonella’s improvement
• Tonella improved this by passing all data
members of an object as actual parameters,
when the object invokes a method.
• But, only few data members might be used in a
method.
• So this method is expensive.

29. Tonella’s improvement (cont.)
• For parameter object, he represented an object
as a single vertex.
• This may yield an imprecise slice.
• At the end of D(), ba.a does not affect o.b .

30. Example
Class Base{ func1( ) {
int a,b; Base o;
virtual vm() { Base ba,
a = a + b ; } ba.m1( );
public: ba.m2(1);
Base( ) { o.m2(1);
a = 0 ; }
b = 0 ; }
m2(int i) { C(Base &ba) {
b = b + i; } ba.m1( );
m1( ) { ba.m2(1); }
if (b > 0) D( ) {
vm( ); Base o;
b = b + 1; } C(o);
} // end of Base o.m2(1) }

31. Dynamic Slicing of OOPs
• Zhao presented the first algorithm, consisting of
two-phases, for dynamic slicing of OOPs.
• Used dynamic object-oriented dependence
graph (DODG) as intermediate representation.
• Defined Slicing Criterion - <s, v, t, i>.
s - statement number
v - variable of interest
t - execution trace
i - input

32. Dynamic Slicing of OOPs(cont.)
• Phase-1: Computing a dynamic slice over
the DODG using DFS/BFS.
• Phase-2: Mapping the slice over the DODG
to source code by defining a mapping
function.

33. DODG of The Example Program

34. Limitations of Zhao’s Approach
• The no.of nodes in a DODG is equal to the no.of
executed statements, which may be unbounded
for programs having many loops.
• Worst case space complexity is O(2n
).
• In the worst case, time complexity becomes
exponential.

35. Motivation
• Slicing is mainly used in interactive applications
such as debugging & testing.
• So, the slicing techniques need to be efficient.
• This requires to develop
- efficient slicing algorithms &
- suitable intermediate representations
• Reports on slicing of OOPs are scarce & less
efficient.
• So, there is a pressing necessity to develop
efficient slicing algorithms for OOPs.

36. Objectives
• Appropriate frame-work to compute slices
- static & dynamic
• Suitable intermediate representation
• Development of efficient dynamic slicing
techniques
• Computing slices of concurrent O-O programs

37. Works done/ Work in progress
• We have proposed an efficient intermediate
representation for representing OOPs.
• We named this as object-oriented system
dependence graph (OSDG).
• We have proposed an algorithm for dynamic
slicing of OOPs.
• We have proposed an algorithm for dynamic
slicing of concurrent OOPs.

38. Our Extended SDG(OSDG)
• For objects present at call site: we use Larson
& Harrold’s representation.
• For parameter object: our OSDG explicitly
represents the data members of the object.
• We represent parameter object as a tree.

39. OSDG (cont.)
• The root represents the object itself.
• Children represent object’s data members.
• The edges represent data dependences
between the object & it’s data members.
• If a data member of an object is another object,
we further expand this data member into a sub-
tree.

40. OSDG (cont.)
• Consider C(o) in function D( ).
• At call site,the actual parameter o is represented
as a tree;
- leaves represent o’s data members a & b.
• From the slice, now ba.a is omitted.

41. OSDG (cont.)
• Polymorphism : lets the type of an object be
decided at run-time.
• We call such an object as polymorphic object.
• We represent a polymorphic object as a tree.

42. OSDG (cont.)
• The root represents the polymorphic object.
• Leaves represent objects of possible types.
• When the polymorphic object is used as a
parameter, the children are further expanded
into trees.

43. Example
class Derived : public Base func2{
{ int i;
int d ; Base *p;
vm( ) { cin>>i;
d = d + b ; if(i > 0)
} p = new Base();
public: Derived(): Base() { else
d = 0; } p = new Derived();
m3() { C(*p);
d = d +1 ; (*p).m(1);
m2(1) ;} }
m4() {
m1(); }
} end of class

44. OSDG of the Example
b a a b b d d b b A-
in
b b A-
in
b
Base Derive
d
Derive
d
Base
ba.m1
()
ba.m2(
1)se
b a a b d a d b a b
Bas
e
Derive
d
Derive
d
Bas
e
a
o
bab
o
C(o
)
A-
in
b
o.m2(1
)se
o.Base(
)
ba
D( )
b
aba
C(Base
&ba)
b
slice
A-in:i-in= 1
Representation for C(Base &) and D( ) in OSDG.

45. Example(cont.)
• The figure shows representation for
C(Base &ba) and D() considering class
Derived and function func2.
• Formal parameter ba is a polymorphic
parameter object.
• So a tree can be used to represent different
references to ba.

46. Slicing the complete program
• Construct the SDG with these modifications
• Use the two-pass algorithm to obtain the slice.

47. Comparison With Other Methods
• It distinguishes data members for different
objects.
• It provides a way to represent object
parameters.
• It represents the effects of polymorphism.

48. Our Dynamic Slicing Algorithm
• We proposed an algorithm known as edge-
marking dynamic slicing algorithm for OOPs.
• SDG is constructed statically only once.
• Based on marking & unmarking the edges as
and when the dependencies arise & cease
during run-time.

49. Our Dynamic Slicing Algorithm(cont.)
• We mark an edge when it’s associated
dependence exists.
• We unmark an edge when the associated
dependence ceases to exist.

50. Current direction of research
• Efficient frame-work and intermediate
representation of OOP.
• Extension of our edge-marking dynamic slicing
algorithm to handle dynamic slicing of
concurrent OOPs.
• Dynamic slicing of distributed OOPs.

51. Publications
• D. P. Mohapatra, R. Mall, R. Kumar, “Dynamic Slicing of Concurrent
Object-Oriented Programs”, In proc. of International Conference on
Information Technology:Progresses & Challenges (ITPC), Kathamandu,
Nepal, pp 283-290, 23-26 May, 2003.
• D. P. Mohapatra, R. Mall, R. Kumar, “An Efficient Technique for Slicing of
Object-Oriented Programs”, In proc. of National Conference on Object-
Oriented Technology (NCOOT), Dr. B. R. Ambedkar Technological
University, Lonere, pp 26-42, 9-10 August, 2003.
• D. P. Mohapatra, R. Mall, R. Kumar, “Dynamic Slicing of Object-
Oriented Programs”, International Conference on Advanced Computing
and Communications (ADCOM)-2003,Coimbatore, December 2003
(Accepted)
• D. P. Mohapatra, G. B. Mund, R. Mall, R. Kumar, “Dynamic Slicing of
Object-Oriented Programs”, International Journal of Software and
Knowledge Engineering, Singapore. (Communicated).

52. Thank You