Rencana pelaksanaan pembelajaran ini membahas tentang transformasi matematika pada materi pokok transformasi untuk siswa kelas XI Program MIPA. Pembelajaran akan meliputi konsep translasi, refleksi, rotasi, dan dilatasi beserta contoh-contohnya dalam kehidupan sehari-hari serta kaitannya dengan konsep matriks. Tujuan pembelajaran adalah agar siswa dapat memahami keempat jenis transformasi tersebut dan mampu men

1. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :1/71
RENCANA PELAKSANAAN PEMBELAJARAN
(RPP)
Nama Madrasah : MA Pondok Pesantren Al-Ikhlas Bone
Mata Pelajaran : Matematika Wajib
Kelas/Program : XI/MIPA
Semester : Ganjil
Materi Pokok : Transformasi
Alokasi Waktu : ... JP (... Pertemuan)
A. Kompetensi Inti (KI)
1. Menghargai dan menghayati ajaran agama yang dianutnya.
2. Menghayati dan mengamalkan perilaku jujur, disiplin, tanggung jawab, peduli (gotong royong,
kerja sama, toleran, damai), santun, responsif dan pro-aktif dan menunjukkan sikap sebagai
bagian dari solusi atas berbagai permasalahan dalam berinteraksi secara efektif dengan
lingkungan sosial dan alam serta dalam menempatkan diri sebagai cerminan bangsa dalam
pergaulan dunia.
3. Memahami, menerapkan, menganalisis pengetahuan faktual, konseptual, prosedural, dan
metakognitif berdasarkan rasa ingin tahunya tentang ilmu pengetahuan, teknologi, seni, budaya,
dan humaniora dengan wawasan kemanusiaan, kebangsaan, kenegaraan, dan peradaban terkait
penyebab fenomena dan kejadian, serta menerapkan pengetahuan prosedural pada bidang
kajian yang spesifik sesuai dengan bakat dan minatnya untuk memecahkan masalah.
4. Mengolah, menalar, dan menyaji dalam ranah konkret dan ranah abstrak terkait dengan
pengembangan dari yang dipelajarinya di sekolah secara mandiri, bertindak secara efektif dan
kreatif serta mampu menggunakan metode sesuai kaidah keilmuan.
B. Kompetensi Dasar dan Indikator Pencapaian Kompetensi :
Kompetensi Dasar Indikator Pencapaian Kompetensi
3.5 Menganalisis dan
membandingkan
transformasi dan
komposisi transformasi
dengan menggunakan
matriks.
3.5.1 Menyebutkan contoh translasi, refleksi, rotasi, dan
dilatasi dalam kehidupan sehari-hari.
3.5.2 Menemukan sifat-sifat translasi, refleksi, rotasi, dan
dilatasi berdasarkan pengamatan pada masalah
kontekstual dan pengamatan objek pada bidang
koordinat.
3.5.3 Menemukan konsep translasi dengan kaitannya dengan
konsep matriks.
3.5.4 Menemukan konsep refleksi terhadap titik 𝑂(0,0) dengan
kaitannya dengan konsep matriks.
3.5.5 Menemukan konsep refleksi terhadap sumbu x dengan
kaitannya dengan konsep matriks.

2. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :2/71
Kompetensi Dasar Indikator Pencapaian Kompetensi
3.5.6 Menemukan konsep refleksi terhadap sumbu y dengan
kaitannya dengan konsep matriks.
3.5.7 Menemukan konsep refleksi terhadap garis 𝑦 = 𝑥 dengan
kaitannya dengan konsep matriks.
3.5.8 Menemukan konsep refleksi terhadap garis 𝑦 = −𝑥
dengan kaitannya dengan konsep matriks.
3.5.9 Menemukan konsep rotasi pada suatu sudut dan pusat
𝑂(0,0) dengan kaitannya dengan konsep matriks.
3.5.10 Menemukan konsep rotasi pada suatu sudut dan pusat
𝑃(𝑝, 𝑞) dengan kaitannya dengan konsep matriks.
3.5.11 Menemukan konsep dilatasi pada faktor skala 𝑘 dan
pusat 𝑂(0,0) dengan kaitannya dengan konsep matriks.
3.5.12 Menemukan konsep dilatasi pada faktor skala 𝑘 dan
pusat 𝑃(𝑝, 𝑞) dengan kaitannya dengan konsep matriks.
3.5.13 Membandingkan keempat jenis transformasi dengan
menyebutkan perbedaannya.
3.5.14 Menemukan konsep komposisi transformasi (translasi,
refleksi, rotasi, dan dilatasi).
4.5 Menyelesaikan masalah
yang berkaitan dengan
matriks transformasi
geometri (translasi,
refleksi, dilatasi, dan
rotasi).
4.5.1 Menemukan matriks transformasi (translasi, refleksi,
rotasi, dan dilatasi) dengan pengamatan terhadap titik-
titik dan bayangannya.
4.5.2 Menggunakan konsep transformasi (translasi, refleksi,
rotasi, dan dilatasi) dengan kaitannya dengan konsep
matriks dalam menemukan koordinat titik atau fungsi
setelah ditransformasi.
4.5.3 Membandingkan proses transformasi (translasi, refleksi,
rotasi, dan dilatasi).
C. Tujuan Pembelajaran :
Pembelajaran materi transformasi melalui pengamatan, tanya jawab, penugasan individu dan
kelompok, diskusi kelompok, dan penemuan (discovery) diharapkan peserta didik dapat:
1. Menyebutkan contoh translasi, refleksi, rotasi, dan dilatasi dalam kehidupan sehari-hari.
2. Menemukan sifat-sifat translasi, refleksi, rotasi, dan dilatasi berdasarkan pengamatan pada
masalah kontekstual dan pengamatan objek pada bidang koordinat.
3. Menemukan konsep translasi dengan kaitannya dengan konsep matriks.
4. Menemukan konsep refleksi terhadap titik 𝑂(0, 0) dengan kaitannya dengan konsep matriks.
5. Menemukan konsep refleksi terhadap sumbu x dengan kaitannya dengan konsep matriks.
6. Menemukan konsep refleksi terhadap sumbu y dengan kaitannya dengan konsep matriks.

3. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :3/71
7. Menemukan konsep refleksi terhadap garis 𝑦 = 𝑥 dengan kaitannya dengan konsep matriks.
8. Menemukan konsep refleksi terhadap garis 𝑦 = −𝑥 dengan kaitannya dengan konsep matriks.
9. Menemukan konsep rotasi pada suatu sudut dan pusat 𝑂(0,0) dengan kaitannya dengan konsep
matriks.
10. Menemukan konsep rotasi pada suatu sudut dan pusat 𝑃(𝑝, 𝑞) dengan kaitannya dengan
konsep matriks.
11. Menemukan konsep dilatasi pada faktor skala 𝑘 dan pusat 𝑂(0,0) dengan kaitannya dengan
konsep matriks.
12. Menemukan konsep dilatasi pada faktor skala 𝑘 dan pusat 𝑃(𝑝, 𝑞) dengan kaitannya dengan
konsep matriks.
13. Membandingkan keempat jenis transformasi dengan menyebutkan perbedaannya.
14. Menemukan konsep komposisi transformasi (translasi, refleksi, rotasi, dan dilatasi).
15. Terampil menemukan matriks transformasi (translasi, refleksi, rotasi, dan dilatasi) dengan
pengamatan terhadap titik-titik dan bayangannya.
16. Terampil menggunakan konsep transformasi (translasi, refleksi, rotasi, dan dilatasi) dengan
kaitannya dengan konsep matriks dalam menemukan koordinat titik atau fungsi setelah
ditransformasi.
17. Terampil membandingkan proses transformasi (translasi, refleksi, rotasi, dan dilatasi).
D. Materi Pembelajaran :
1. Fakta:
a. Translasi (Pergeseran)
Mahreen Zaura Moza Dissa Nasya Brice
<<--------Baris--------
Tsakifa Edrea Brinets Givri Ullyn Charissa
Farissa Hennania Alma There Siti Hafiz
Jafni Fayhaq Ephraim Tsaqif Catur Muhtadi
Fadzil Zhafran Ubaidillah Yazid Shabir Xavier
Kafka Bilal Ghazi Uzreem Tiffal Ahmad
----------- Lajur ----------->> Guru
Gambar 1: Ilustrasi Denah Kelas
Suasana pembelajaran di kelas XI MIA 1 pekan lalu tampaknya kurang efektif sebab
banyak peserta didik yang tidak memperhatikan penjelasan guru, melainkan mereka
melakukan kegiatan lain seperti berbicara dengan teman yang ada disebalahnya. Hal ini
dibuktikan oleh laporan beberapa guru mapel ke wali kelas. Untuk mengatasi hal tersebut,
wali kelas XI MIA 1 berinisiatif memindahkan posisi tempat duduk beberapa peserta didik
agar mereka yang sering mengobrol saat guru memberikan pelajaran tidak lagi duduk
berdekatan.
Perubahan yang terjadi di kelas tersebut sebagai berikut: pekan lalu, Ahmad duduk di
pojok kanan baris pertama di kelasnya. Pekan ini, ia berpindah ke baris ketiga jalur keempat

4. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :4/71
yang minggu lalu ditempati Tsaqif. Tsaqif sendiri berpindah ke baris kedua lajur kedua yang
minggu lalu ditempati Zhafran, sementara Zhafran saat ini menempat posisi Ahmad minggu
lalu.
Dari ilustrasi di atas, formasi peserta didik tersebut dapat digambarkan ke dalam
koordinat kartesius. Dapatkah kita tentukan pola pergesaran ke tiga peserta didik tersebut?
b. Refleksi (Pencerminan)
Gambar 2: Orang Bercermin
Kalian pasti sering bercermin. Ketika bercermin, amatilah diri dan bayangan kalian.
Apakah memiliki bentuk dan ukuran yang sama? Amati pula jarak diri kalian ke cermin.
Samakah dengan jarak bayangan kalian ke cermin? Dengan bercermin dan menjawab
pertanyaan-pertanyaan tersebut, kalian akan menemukan beberapa sifat pencerminan.
Seandainya permasalah ini dibawa ke pendekatan koordinat kartesius dengan memisahkan
kembali bahwa objek yang dicerminkan adalah sebuah titik pada koordinat kartesius dengan
cermin tersebut adalah sebuah garis, dapatkah kita temukan hubungan koordinat objek
dengan koordinat bayangannya?
c. Rotasi (Perputaran)
Gambar 3: Peserta Didik Membuat Busur Lingkaran Menggunakan Jangka
Anis membuat sebuah busur lingkaran dengan menggunakan jangka. Ia menusukkan
jarum jangka pada titik O, kemudian memutar jangka dengan sudut putar berlawanan dengan
arah perputaran jarum jam. Melalui peragaan ini, Anis telah melakukan rotasi sebesar a
dengan pusat titik O. Misalkan, posisi awal pensil jangka pada titik A(a, b). Dapatkah kamu
menemukan posisi pensil jangka setelah dirotasi?

5. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :5/71
d. Dilatasi
Gambar 4: Peserta didik berkunjung ke IPTN
Wilby dan teman-temannya berkunjung ke IPTN. Di sana, mereka mengamati miniatur
sebuah pesawat terbang. Miniatur pesawat terbang ini mempunyai bentuk yang sama
dengan pesawat terbang sesungguhnya, tetapi ukurannya lebih kecil. Bentuk seperti miniatur
pesawat terbang ini telah mengalami dilatasi diperkecil dari pesawat terbang sesungguhnya.
Selain dilatasi diperkecil, terdapat pula dilatasi diperbesar. Apa yang dapat kamu simpulkan
berdasarkan pengamatan yang dilakukan oleh Wilby?
e. Komposisi Transformasi
Gambar 5: Salon
Coba kamu amati cermin di tukang cukur (atau salon). Di depan kita ada cermin dan di
belakang kita juga terdapat cermin. Jadi, kamu memiliki bayangan di cermin di depanmu dan
di belakangmu, bukan? Jika kamu amati lebih lanjut, bayanganmu di cermin depan akan
mempunyai bayangan juga di cermin belakang dan sebaliknya. Hal ini menunjukkan terjadi
pencerminan bertahap dengan dirimu sebagai objek. Nah, ini akan melahirkan konsep
komposisi transformasi khususnya refleksi. Dapatkah kamu menemukan konsep komposisi
refleksi?

6. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :6/71
2. Konsep:
a. Definisi Translasi
Translasi adalah suatu transformasi yang memindahkan setiap titik pada sebuah
bidang berdasarkan jarak dan arah tertentu. Misalkan 𝑥, 𝑦, 𝑎, 𝑏 ∈ ℝ, translasi titik 𝐴(𝑥, 𝑦)
dengan 𝑇(𝑎, 𝑏) menggeser absis 𝑥 sejauh 𝑎 dan bergeser ordinat 𝑦 sejauh 𝑏, sehingga
diperoleh titik 𝐴′( 𝑥+ 𝑎, 𝑦 + 𝑏), secara notasi ditulis:
𝐴 (
𝑥
𝑦)
𝑟( 𝑎
𝑏
)
→ 𝐴′(
𝑥 + 𝑎
𝑦 + 𝑏)
b. Definisi Refleksi
Refleksi adalah suatu jenis transformasi yang memindahkan setiap titik pada suatu
bidang dengan menggunakan sifat bayangan cermin dari titik-titik yang dipindahkan. Jika
terdapat sebarang titik 𝑃(𝑎, 𝑏), akan terdapat beberapa definisi pencerminan yaitu sebagai
berikut:
Jenis Pencerminan Notasi Bentuk Matriks
Terhadap titik (0,0) 𝐴 (
𝑎
𝑏
)
𝑅 𝑂(0,0)
→ 𝐴′(
−𝑎
−𝑏
) (
−𝑎
−𝑏
) = (
−1 0
0 −1
) (
𝑎
𝑏
)
Terhadap sumbu 𝑥 𝐴 (
𝑎
𝑏
)
𝑅 𝑠𝑢𝑚𝑏𝑢 𝑥
→ 𝐴′(
𝑎
−𝑏
) (
−𝑎
−𝑏
) = (
1 0
0 −1
)(
𝑎
𝑏
)
Terhadap sumbu 𝑦 𝐴(
𝑎
𝑏
)
𝑅 𝑠𝑢𝑚𝑏𝑢 𝑦
→ 𝐴′(
−𝑎
𝑏
) (
−𝑎
−𝑏
) = (
−1 0
0 1
)(
𝑎
𝑏
)
Terhadap garis 𝑦 = 𝑥 𝐴(
𝑎
𝑏
)
𝑅 𝑦=𝑥
→ 𝐴′(
𝑎
𝑏
) (
−𝑎
−𝑏
) = (
1 0
0 1
) (
𝑎
𝑏
)
c. Definisi Rotasi
Rotasi adalah transformasi yang memindahkan suatu titik ke titik lain dengan
perputaran terhadap titik pusat tertentu. Jika titik 𝐴(𝑎, 𝑏) dirotasikan dengan matriks rotasi 𝑀 𝑅
dan pusat 𝑃(𝑝, 𝑞) dan 𝐴′(𝑏, 𝑎) dituliskan:
( 𝑎′
𝑏′
) = 𝑀 𝑅 (
𝑎 − 𝑝
𝑏 − 𝑞) + (
𝑝
𝑞)
d. Definisi Dilatasi
Dilatasi adalah suatu transformasi yang memperbesar atau memperkecil bangun tetapi
tidak mengubah bentuk. Dilatasi dengan pusat 𝑃(𝑝, 𝑞) dari faktor skala 𝑘 𝐴(𝑎, 𝑏)
𝑐[𝑃( 𝑝,𝑞),𝑘]
→ 𝐴′ ( 𝑏
𝑎
)
dengan
( 𝑎′
𝑏′
) = 𝑘 (
𝑎 − 𝑝
𝑏 − 𝑞) + (
𝑝
𝑞)
e. Definisi Kompsisi Transformasi
Matriks Komposisi Translasi
Jika matriks translasi 𝑇1 adalah (
𝑎
𝑏
) dan matriks translasi 𝑇2 adalah (
𝑐
𝑑
) maka matriks
komposisi translasi 𝑇1 ○ 𝑇2 atau 𝑇2 ○ 𝑇1 dituliskan,
𝑀 𝑇1○𝑇2
= 𝑀 𝑇1
+ 𝑀 𝑇2
= (
𝑎
𝑏
) + (
𝑐
𝑑
)
𝑀 𝑇2○𝑇1
= 𝑀 𝑇2
+ 𝑀 𝑇1
= (
𝑐
𝑑
) + (
𝑎
𝑏
)

7. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :7/71
Matriks Komposisi Refleksi
Jika matriks refleksi 𝐶1 adalah(
𝑎 𝑏
𝑐 𝑑
) dan refleksi 𝐶2 adalah (
𝑒 𝑓
𝑔 ℎ
) maka matriks
komposisi refleksi 𝐶1 ○ 𝐶2 atau 𝐶2 ○ 𝐶1 dituliskan,
𝑀 𝐶1
○ 𝑀 𝐶2
= 𝑀 𝐶1
𝑀 𝐶2
= (
𝑎 𝑏
𝑐 𝑑
) (
𝑒 𝑓
𝑔 ℎ
)
𝑀 𝐶2
○ 𝑀 𝐶1
= 𝑀 𝐶2
𝑀 𝐶1
= (
𝑒 𝑓
𝑔 ℎ
) (
𝑎 𝑏
𝑐 𝑑
)
Hasil perkalian 𝑀 𝐶1
𝑀 𝐶2
dan 𝑀 𝐶2
𝑀 𝐶1
belum tentu sama.
Matriks Komposisi Rotasi
Jika 𝑅1[0,𝛼1] dan 𝑅2[0,𝛼2] adalah rotasi sebesar 𝛼1 pada sudut 𝑂(0,0) dan rotasi sebesar
𝛼2 pada sudut 𝑂(0,0) maka matriks komposisi ditulis,
𝑀( 𝑅1[0,𝛼1],𝑅2[0,𝛼2]) = (
cos(𝛼2 + 𝛼1) −sin(𝛼2 + 𝛼1)
sin(𝛼2 + 𝛼1) cos(𝛼2 + 𝛼1)
)
Matriks Komposisi Dilatasi
Jika 𝐴(𝑥, 𝑦) dirotasi berturut-turut oleh𝐷1[0,𝑘1] dan 𝐷2[0,𝑘2] maka,
( 𝐷2 ○ 𝐷1) ((
𝑥
𝑦)) = 𝑘2 𝑘1(
𝑥
𝑦)
3. Prinsip:
a. Sifat-sifat dari translasi
 Bangun yang digeser (ditranslasikan) tidak mengalami perubahan bentuk dan ukuran.
 Bangun yang digeser (ditranslasikan) mengalami perubahan posisi.
b. Sifat-sifat dari refleksi
 Bangun (objek) yang dicerminkan (refleksi) tidak mengalami perubahan bentuk dan
ukuran.
 Jarak bangun (objek) dari cermin (cermin datar) adalah sama dengan jarak bayangan
dengan cermin tersebut.
c. Sifat-sifat dari rotasi
 Bangun yang diputar (rotasi) tidak mengalami perubahan bentuk dan ukuran.
 Bangun yang diputar (rotasi) mengalami perubahan posisi.
d. Sifat-sifat dari dilatasi
 Bangun yang diperbesar atau diperkecil (dilatasi) dengan skala 𝑘 dapat mengubah
ukuran atau tetap ukurannya tetapi tidak mengubah bentuk. Jika 𝑘 > 1 maka bangun akar
diperbesar dan terletak searah terhadap pusat dilatasi dengan bangun semula.
 Bangun yang diperbesar atau diperkecil (dilatasi) dengan skala 𝑘 dapat mengubah
ukuran tetapi tidak mengubah bentuk. Jika 𝑘 > 1 maka bangun tidak mengalami
perubahan ukuran dan letak.
 Bangun yang diperbesar atau diperkecil (dilatasi) dengan skala k dapat mengubah ukuran
tetapi tidak mengubah bentuk. Jika 0 < 𝑘 < 1 maka bangun akan diperkecil dan terletak
searah terhadap pusat dilatasi dengan bangun semula .

8. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :8/71
 Bangun yang diperbesar atau diperkecil (dilatasi) dengan skala k dapat mengubah ukuran
atau tetap ukurannya tetapi tidak mengubah bentuk. Jika −1 < 𝑘 < 0 – 1 maka bangun
akan diperkecil dan terletak berlawanan arah terhadap pusat dilatasi dengan bangun
semula.
 Bangun yang diperbesar atau diperkecil (dilatasi) dengan skala k dapat mengubah ukuran
atau tetap ukurannya tetapi tidak mengubah bentuk. Jika 𝑘 <– 1 maka bangun akan
diperbesar dan terletak berlawanan arah terhadap pusat dilatasi dengan bangun semula.
4. Prosedur:
a. Langkah-langkah mengoperasikan dan mengombinasikan unsur-unsur dari translasi.
b. Langkah-langkah mengoperasikan dan mengombinasikan unsur-unsur dari refleksi.
c. Langkah-langkah mengoperasikan dan mengombinasikan unsur-unsur dari rotasi.
d. Langkah-langkah mengoperasikan dan mengombinasikan unsur-unsur dari dilasi.
e. Langkah-langkah mengoperasikan dan mengombinasikan unsur-unsur dari komposisi trans-
formasi.
E. Metode dan Model Pembelajaran :
Model pembelajaran : Treffinger (Translasi)
Discovery Learning (Refleksi)
Discovery Learning (Rotasi)
Treffinger (Dilatasi)
Direct Instruction (Komposisi Transformasi)
Pendekatan : Scientific
Metode Pembelajaran : Diskusi, Eksperimen, Tanya Jawab dan Penugasan
F. Media Pembelajaran :
Media : White Board, Tayangan Power Point dan Lembar Kerja Peserta Didik
Alat : Laptop, LCD
G. Sumber Belajar :
1. Kementerian Pendidikan dan Kebudayaan. 2017 (Edisi Revisi 2017). Buku Guru Mata Pelajaran
Matematika (Wajib) kelas XI. Jakarta: Kementerian Pendidikan dan Kebudayaan.
2. Kementerian Pendidikan dan Kebudayaan. 2017 (Edisi Revisi 2017). Buku Siswa Mata Pelajaran
Matematika (Wajib) kelas XI. Jakarta: Kementerian Pendidikan dan Kebudayaan.
3. Buku Pengayaan/Pendamping Buku Paket.
 Pesta dan Cecep Anwar. 2008. Matematika Aplikasi untuk SMA dan MA Kelas XII Program
Studi Ilmu Alam (BSE). Jakarta: Pusat Perbukuan Dapartemen Pendidikan Nasional.
 Tim BBM. 2015. Big Book Matematika Kelas 1, 2 & 3 (BSE). Jakarta: Penerbit Cmedia.
 Wirodikromo, S. 2007. Matematika SMA: untuk SMA Kelas XII IPA. Jakarta: Erlangga.
4. Kumpulan Soal-Soal UN atau SBMPTN.

9. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :9/71
H. Langkah-langkah Pembelajaran :
Translasi (Pertemuan ......../..... JP)
1. Kegiatan Pendahuluan (±15 menit):
Orientasi
a. Melakukan pembukaan dengan mengucapkan salam pembuka.
b. Meminta ketua kelas (atau seorang peserta didik) untuk memimpin doa sebelum memulai pem-
belajaran.
c. Memeriksa kehadiran peserta didik sebagai sikap disiplin.
d. Menyiapkan fisik dan psikis peserta didik dalam mengawali kegiatan pembelajaran.
Motivasi
a. Memberikan gambaran tentang pentingnya memahami konsep translasi, serta memberikan gam-
baran tentang penggunaannya dalam kehidupan sehari-hari.
b. Menyampaikan tujuan pembelajaran pada pertemuan yang berlangsung.
c. Mengajukan pertanyaan.
Apersepsi
a. Mengaitkan materi pembelajaran yang akan dilakukan dengan pengalaman peserta didik dengan
materi sebelumnya.
b. Mengingatkan kembali materi prasyarat dengan bertanya mengenai materi fungsi, trigonometri
dan matriks yang telah dipelajari di kelas X serta materi transformasi geometri (khususnya trans-
lasi) yang telah dipelajari di SMP.
c. Menyampaikan informasi yang ada keterkaitannya dengan pelajaran yang akan dilakukan.
 Informasikan kepada peserta didik bahwa konsep transformasi ini dikaji dengan pendekatan
koordinat dan hubungannya dengan konsep matriks.
 Memberikan beberapa contoh yang berkaitan dengan translasi di kehidupan nyata:
 Kendaraan yang bergerak di jalan raya atau pesawat terbang yang melintas di udara.
 Bahkan diri kita sendiri yang bergerak kemana saja.
 Berilah kesempatan kepada peserta didik untuk memikirkan posisi, bentuk dan ukuran objek
yang berpindah (bertranslasi) tersebut.
 Informasikan kepada peserta didik bahwa pergerakan objek-objek tersebut akan dibahas
dengan pendekatan koordinat.
 Membuat asumsi dengan peserta didik, bahwa pergerakan ke arah sumbu 𝑥 positif adalah ke
kanan, pergerakan ke arah sumbu 𝑥 negatif adalah ke kiri, pergerakan ke arah sumbu 𝑦
positif adalah ke atas dan pergerakan ke arah sumbu 𝑦 negatif adalah ke bawah.
 Berdasarkan masalah dan kegiatan yang diberikan pada buku siswa, instruksikan peserta
didik agar mampu memahami materi translasi.
Pemberian Acuan
a. Memberitahukan materi pelajaran yang akan dibahas pada pertemuan saat itu.
b. Memberitahukan tentang kompetensi inti, kompetensi dasar, indikator, dan KKM pada pertemuan
yang berlangsung.

10. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :10/71
c. Pembagian kelompok belajar.
d. Menjelaskan mekanisme pelaksanaan pengalaman belajar sesuai dengan langkah-langkah
pembelajaran.
2. Kegiatan Inti (±60 menit):
 Peserta didik bergabung bersama teman kelompoknya dengan tertib dan hemat waktu.
 Peserta didik mendapatkan motivasi agar tetap tekun, serius dan kompak dalam belajar.
Fase 1: Memahami Tantangan
Menggali Data
a. Peserta didik menyebutkan atau mengamati benda-benda yang bergerak atau bergeser dalam
kehidupan sehari-hari.
b. Peserta didik diberi kesempatan untuk memahami sifat pergeseran (translasi) dengan menga-
mati benda-benda yang bergerak di lingkungan sekitar. Mengarahkan peserta didik fokus pada
bentuk dan ukuran benda-benda yang bergerak tersebut.
c. Peserta didik secara bergantian memperagakan pergeseran (translasi) benda-benda di depan
kelas sebagai media.
d. Peserta didik mendapatkan kesempatan untuk mengomunikasikan pendapatnya tentang perge-
seran benda-benda setelah diamati.
e. Peserta didik diarahkan agar jawaban yang diberikan fokus pada bentuk dan ukuran benda
setelah pergeseran.
f. Pendidik mengecek solusi yang telah diperoleh peserta didik dan memberikan permasalahan
baru namun lebih kompleks agar peserta didik dapat menerapkan solusi yang telah ia peroleh.
Masalah 4.1
a. Peserta didik diarahkan untuk memahami pergeseran (translasi) suatu titik di bidang koordinat.
b. Peserta didik membaca Masalah 4.1. pada buku siswa yaitu:
Titik 𝐴(4,– 3) bergerak ke kiri 6 langkah dan ke bawah 1 langkah, kemudian dilanjutkan kembali
bergerak ke kiri 3 langkah dan ke atas 3 langkah. Coba kamu sketsa pergerakan titik tersebut
pada bidang koordinat kartesius. Dapatkah kamu temukan proses pergerakan titik tersebut?
c. Peserta didik diberikan stimulus dengan cara meminta peserta didik menunjukkan pergeseran
titik pada bidang koordinat kartesius dan membaca koordinat perubahannya setelah bergeser.
d. Peserta didik dan pendidik membuat kesepakatan mengenai arah pergeseran pada sumbu
koordinat yakni: arah pergeseran ke kiri (sebagai sumbu 𝑥 negatif), ke kanan (sebagai sumbu 𝑥
positif), ke atas (sebagai sumbu 𝑦 positif) dan ke bawah (sebagai sumbu y negatif).
e. Peserta didik mengamati dan memahami konsep pergeseran (translasi) ke bentuk matriks pada
alternatif penyelesaian Masalah 4.1 pada buku siswa.
f. Peserta didik diberikan stimulus untuk bertanya agar dapat dipastikan setiap kelompok apat
bekerja sama, terlibat aktif dalam merumuskan konsep yang akan dicapai.
d. Seorang peserta didik yang terpilih secara acak mengomunikasikan pendapatnya tentang
pergeseran pada Masalah 4.1.

11. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :11/71
e. Peserta didik lainnya diberikan kesempatan untuk bertanya atau memberikan pendapat. Pendidik
memantau pendapat peserta didik tersebut serta memperbaiki jika ada pendapat yang tidak
sesuai konsep.
f. Peserta didik yang tidak atau kurang aktif diberikan umpan balik untuk menumbuhkan keaktifan
belajarnya.
Masalah 4.2
a. Peserta didik memperkuat pemahamannya tentang pergeseran dengan mengajukan masalah 4.2
untuk dibaca dan dipahami serta diberi komentar, yakni: bagaimana jika sebuah bidang digeser
pada bidang koordinat kartesius? Coba kamu amati bidang segitiga ABC yang digeser pada
gambar berikut! Dapatkah kamu menentukan arah dan besar pergeserannya?
b. Peserta didik diarahkan untuk mengamati posisi, bentuk dan ukuran objek sebelum dan sesudah
perge-seran, adakah perubahan yang terjadi?
c. Peserta didik diarahkan ke sesi tanya jawab di antara peserta didik. Pendidik memantau kebe-
naran pendaat-pendapat peserta didik.
d. Peserta didik mengembangkan sikap kritis dengan cara menjawab pertanyaan:
 Apakah terdapat perbedaan pergeseran ketiga titik sudut pada segitiga ABC?.
e. Peserta didik diarahkan untuk mencermati sifat 4.1 dan melengkapi tabel 4.1 translasi titik
dengan mengamati konsep translasi pada buku siswa halaman 130.
f. Peserta didik mengomunikasikan pendapatnya tentang mengamati posisi, bentuk dan ukuran
objek semebelum dan sesduah pergeseran.
g. Pendapat yang dikemukakan peserta didik dipantau oleh pendidik serta diperbaiki jika terdapat
pendapat yang tidak sesuai konsep.
h. Peserta didik yang lain diberikan kesempatan untuk mengemukakan gagasannya secara sopan
dan hemat waktu, apabila terdapat hal yang dianggap berbeda atau bertetangan.
i. Peserta didik memperoleh penegasan terhadap solusi yang diperoleh serta motivasi agar terlibat
aktif dalam proses pembelajaran.
Merumuskan Masalah
a. Untuk mendapatkan tingkat pemahaman peserta didik akan konsep pergeseran/translasi,
peserta didik menyelesaikan masalah yang disajikan di LKPD (Kode 4a).

12. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :12/71
b. Peserta didik diarahkan mengingat kembali konsep translasi yang telah dipelajari sebelumnya.
c. Peserta didik memperhatikan penjelasan informasi masalah yang akan diamati.
d. Peserta didik mengamati dan mencermati masalah.
e. Peserta didik diberikan kesempatan untuk mengidentifikasi permasalahan.
f. peserta didik diberikan gambaran mengenai masalah yang telah dirumuskan dengan diskusi dan
tanya jawab.
g. Peserta didik diberikan stimulus dengan cara menjawab pertanyaan yang memerlukan analisis.
Misalnya: apakah posisi, bentuk dan ukuran rumah Abiyyu akan berubah jika dilakukan perge-
seran (translasi) ke samping lapangan sepak bola (masalah LKPD).
h. Peserta didik menanya atau mendiskusikan (antar peserta didik dalam satu kelompok atau diluar
kelompok, dan/atau pendidik) tentang masalah yang diamati.
Fase 2: Membangkitkan Gagasan
a. Peserta didik diberikan waktu dan kesempatan untuk mengungkapkan gagasan dan membentuk
jejaring dengan cara diskusi kelompok serta membimbimbing peserta didik untuk menyepakati
alternatif pemecahan yang akan di uji.
b. Peserta didik menuliskan informasi yang terdapat pada masalah tersebut secara teliti dengan
menggunakan bahasa sendiri yang mudah dipahami.
c. Kelompok yang melenceng dari pekerjaannya atau mengalami kesulitan dalam menyelesaikan
masalah diberi bimbingan langsung atau bimbingan secara klasikal.
Fase 3: Mempersiapkan Tindakan
Mengembangkan Solusi
a. Peserta didik mengumpulkan informasi yang sesuai dari berbagai sumber belajar yang tersedia
atau melaksanakan eksperimen untuk mendapatkan penjelasan dan pemecahan masalah
b. Peserta didik mengidentifikasi masalah dan menalar bagaimana cara menemukan solusi.
c. Peserta didik mengamati contoh 4.1 dan contoh 4.2 beserta alternatif penyelesaiannya pada
buku siswa sebagai informasi tambahan untuk menyelesaikan masalah pada LKPD (Kode 4a).
d. Kelompok yang telah menemukan penyelesaian masalahnya diinstruksikan untuk memeriksa
kembali secara detail solusi yang diperoleh.
e. Peserta didik yang ditunjuk sebagai ketua dalam kelompoknya diingatkan untuk meyakinkan
bahwa tiap anggota telah mengetahui dan memahami masalah yang didiskusikan.
f. Masing-masing kelompok yang telah menemukan solusi yang diyakini tepat, selanjutnya menu-
liskan hasil yang diperoleh pada buku latihan atau LKPD yang telah disediakan.
Membangun Penerimaan
a. Satu kelompok dipilih secara acak untuk mempresentasikan hasil diskusinya.
b. Kelompok yang terpilih, selanjutnya bermusyawarah dengan hemat waktu untuk menentukan
seorang diantara mereka yang akan bertindak sebagai juri bicara.
c. Juru bicara yang terpilih menyajikan hasil diskusi kelompoknya di depan kelas dan anggota
kelompok yang tidak bertindak sebagai juru bicara dipersiapkan untuk menjawab tanggapan
ataupun pertanyaan dari kelompok lain.

13. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :13/71
d. Kelompok lain diberikan kesempatan untuk mengajukan pertanyaan mengenai hal-hal yang tidak
dipahami atau terdapat hal-hal yang berbeda antara hasil diskusi dalam kelompok dan presentasi
yang telah dilakukan oleh juru bicara.
e. Anggota kelompok penyaji (kecuali presenter) diberikan kesempatan untuk menanggapi atau
memberi respons terhadap pertanyaan yang masuk.
f. Peserta didik dilibatkan untuk mengevaluasi jawaban kelompok penyaji serta masukan dari
peserta didik lain dan membuat kesepakatan, bila jawaban yang disampaikan sudah tepat.
3. Kegiatan Penutup (±15 menit):
a. Peserta didik diminta menyimpulkan konsep translasi.
b. Memberi penegasan mengenai kesimpulan yang dikemukakan peserta didik mengenai konsep
translasi.
c. Secara individu peserta didik melakukan refleksi (penilaian diri) tentang apa saja yang telah
dipelajari, mengidentifikasi manfaatnya, mengidentifikasi hal-hal yang sudah dan belum dipahami
untuk ditindak lanjuti.
d. Memberikan tugas.
e. Memberikan kuis.
f. Mengakhiri kegiatan belajar dan berpesan untuk mempelajari materi refleksi yang akan dibahas
pada pertemuan selanjutnya.
g. Bersama-sama dengan peserta didik berdoa untuk bersyukur kepada Allah SWT telah diberi
pengetahuan tentang pembelajaran yang telah dilakukan.
h. Mengakhiri pembelajaran dengan mengucapkan salam.
Refleksi (Pertemuan ......../..... JP)
1. Kegiatan Pendahuluan (±15 menit):
Orientasi
a. Melakukan pembukaan dengan mengucapkan salam pembuka.
b. Meminta ketua kelas untuk memimpin doa sebelum memulai pembelajaran.
c. Memeriksa kehadiran peserta didik sebagai sikap disiplin.
d. Menyiapkan fisik dan psikis peserta didik dalam mengawali kegiatan pembelajaran.
Fase 1: Stimulation (Stimulasi/Pemberian Rangsangan)
Motivasi
a. Memberikan gambaran tentang pentingnya memahami konsep refleksi, serta memberikan gam-
baran tentang penggunaannya dalam kehidupan sehari-hari.
b. Menyampaikan tujuan pembelajaran pada pertemuan yang berlangsung.
c. Mengajukan pertanyaan.
Apersepsi
a. Mengaitkan materi pembelajaran yang akan dilakukan dengan pengalaman peserta didik dengan
materi sebelumnya.

14. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :14/71
b. Mengingatkan kembali materi prasyarat dengan bertanya mengenai materi fungsi, trigonometri
dan matriks yang telah dipelajari di kelas X serta materi transformasi geometri (khususnya ref-
leksi) yang telah dipelajari di SMP.
c. Mengajukan pertanyaan yang ada keterkaitannya dengan pelajaran yang akan dilakukan.
 Informasikan kepada peserta didik bahwa konsep transformasi ini dikaji dengan pendekatan
koordinat dan hubungannya dengan konsep matriks.
 Memberikan beberapa pertanyaan yang mengarah pada contoh yang berkaitan dengan
refleksi di kehidupan nyata:
 Pernahkah kalian perhatikan bayangan yang ada pada cermin ketika kalian bercermin?
 Menyajikan beberapa gambar dan menyanyakan ke peserta didik, apakah gambar yang
disajikan adalah pencerminan?
Gambar 6: Contoh Pencerminan
 Berilah kesempatan kepada peserta didik untuk memikirkan posisi, bentuk dan ukuran objek
yang dicerminkan (refleksi) tersebut.
 Informasikan kepada peserta didik bahwa pergerakan objek-objek tersebut akan dibahas
dengan pendekatan koordinat.
 Membuat asumsi dengan peserta didik, bahwa pergerakan ke arah sumbu 𝑥 positif adalah ke
kanan, pergerakan ke arah sumbu 𝑥 negatif adalah ke kiri, pergerakan ke arah sumbu 𝑦
positif adalah ke atas dan pergerakan ke arah sumbu 𝑦 negatif adalah ke bawah.
 Berdasarkan masalah dan kegiatan yang diberikan pada buku siswa, instruksikan peserta
didik agar mampu memahami materi refleksi.
Pemberian Acuan
a. Memberitahukan materi pelajaran yang akan dibahas pada pertemuan saat itu.
b. Memberitahukan tentang kompetensi inti, kompetensi dasar, indikator, dan KKM pada pertemuan
yang berlangsung.
c. Pembagian kelompok belajar.
Menjelaskan mekanisme pelaksanaan pengalaman belajar sesuai dengan langkah-langkah
pembelajaran.
2. Kegiatan Inti (±60 menit):
 Peserta didik bergabung bersama teman kelompoknya dengan tertib dan hemat waktu.
 Peserta didik diberikan motivasi agar tetap tekun, serius dan kompak dalam belajar.

15. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :15/71
 Peserta didik memperhatikan ilustrasi konsep pencerminan yang disampaikan pendidik. Peserta
didik diarahkan memahami sifat “jarak objek terhadap cermin sama dengan jarak bayangan
terhadap cermin”. Peserta didik memperoleh informasi bahwa cermin yang digunakan adalah
cermin datar.
 Peserta didik memperhatikan dengan saksama informasi yang disampaikan pendidik bahwa
konsep pencerminan yang dipelajari adalah pencerminan dengan pendekatan koordinat. Cermin
pada bidang koordinat adalah titik 𝑂(0,0), sumbu 𝑥, sumbu 𝑦, garis 𝑦 = 𝑥 dan garis 𝑦 = −𝑥.
Fase 2: Problem Statement (Pernyataan/Identifikasi Masalah)
a. Peserta didik berdiskusi dengan kelompoknya masing-masing tentang masalah 4.3. Peserta didik
diarahkan mengamati Gambar 4.4.
b. Peserta didik diarahkann fokus berdiskusi pada jarak, bentuk dan ukuran antara objek dan
bayangannya oleh pencerminan pada Gambar 4.4.
d. Peserta didik memberi pendapatnya tentang Masalah 4.3 dan Gambar 4.4 secara sistematis,
sopan dan hemat waktu.
e. Peserta didik mengamati dan mencermati media atau gambar lainnya pada bidang koordinat
untuk memperkuat pemahaman peserta didik akan konsep pencerminan.
f. Peserta didik menuliskan informasi yang diperoleh pada buku catatan.
g. Pendidik bersama-sama dengan peserta didik membangun sifat pencerminan, yakni:
Bangun yang dicerminkan (refleksi) dengan cermin datar tidak mengalami perubahan bentuk dan
ukuran. Jarak bangun dengan cermin (cermin datar) adalah sama dengan jarak bayangan
dengan cermin tersebut.
g. Peserta didik mengamati buku siswa yakni membaca dan memahami:
 Pencerminan terhadap titik 𝑂(0,0) melalui Gambar 4.5.
 Pencerminan terhadap sumbu 𝑥 melalui Gambar 4.6.
 Pencerminan terhadap sumbu 𝑦 melalui Gambar 4.7.
 Pencerminan terhadap garis 𝑥 = 𝑦 melalui Gambar 4.8.
 Pencerminan terhadap garis 𝑦 = −𝑥 melalui Gambar 4.9.
h. Peserta didik memperhatikan koordinat objek dan bayangannya oleh pencerminan:
 Terhadap titik 𝑂(0,0) pada Gambar 4.5, kemudian minta peserta didik melengkapi tabel 4.2
pada halaman 134 buku siswa. Tabel 4.2 terisi sebagai berikut:
Tabel 4.2: Koordinat Pencerminan Titik terhadap Titik 𝑂(0,0)
Titik Bayangan
𝐴(6,3) 𝐴′(−6,−3)
𝐵(−2,2) 𝐵′(2,−2)
𝐶(7, −2) 𝐶′(−7,2)
𝐷(1,−3) 𝐷′(−1,3)
𝐸(2,3) 𝐸′(−2,−3)
 Terhadap sumbu 𝑥 pada Gambar 4.6, kemudian minta peserta didik melengkapi tabel 4.3
pada halaman 137 buku siswa. Tabel 4.3 terisi sebagai berikut:

16. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :16/71
Tabel 4.3: Koordinat Pencerminan Titik terhadap sumbu 𝑥
Titik Bayangan
𝐴(1,1) 𝐴′(1,−1)
𝐵(3,2) 𝐵′(3,−2)
𝐶(6,3) 𝐶′(6,−3)
𝐷(−2, −2) 𝐷′(−2,2)
𝐸(−4,4) 𝐸′(−4,−4)
𝐹(−7,−5) 𝐹′(−7,5)
 Terhadap sumbu 𝑦 pada Gambar 4.7, kemudian minta peserta didik melengkapi tabel 4.4
pada halaman 141 buku siswa. Tabel 4.4 terisi sebagai berikut:
Tabel 4.4: Koordinat Pencerminan Titik terhadap sumbu 𝑦
Titik Bayangan
𝐴(−10,−5) 𝐴′(10,−5)
𝐵(−8, −3) 𝐵′(8,−3)
𝐶(−6,−1) 𝐶′(6,−1)
𝐷(4,1) 𝐷′(−4,1)
𝐸(2,3) 𝐸′(−2,3)
𝐹(1,4) 𝐹′(−1,4)
 Terhadap garis 𝑥 = 𝑦 pada Gambar 4.8, kemudian minta peserta didik melengkapi tabel 4.5
pada halaman 144 buku siswa. Tabel 4.5 terisi sebagai berikut:
Tabel 4.5: Koordinat Pencerminan Titik terhadap garis 𝑥 = 𝑦
Titik Bayangan
𝐴(−1,−5) 𝐴′(−5,−1)
𝐵(3,−5) 𝐵′(−5,3)
𝐶(−2,3) 𝐶′(3,−2)
𝐷(0,4) 𝐷′(4,0)
𝐸(2,4) 𝐸′(4,2)
 Terhadap garis 𝑦 = −𝑥 pada Gambar 4.9, kemudian minta peserta didik melengkapi tabel 4.6
pada halaman 147 buku siswa. Tabel 4.6 terisi sebagai berikut:
Tabel 4.6: Koordinat Pencerminan Titik terhadap garis 𝑦 = −𝑥
Titik Bayangan
𝐴1,−4) 𝐴′(4,−1)
𝐵(−2, −3) 𝐵′(3,2)
𝐶(−5,−3) 𝐶′(3,5)
𝐷(−1,5) 𝐷′(−5,1)
𝐸(−3,5) 𝐸′(−5,3)
i. Peserta didik diharapkan mengidentifikasi sebanyak mungkin pertanyaan yang berkaitan dengan
masalah yang diberikan.
j. Peserta didik diberikan stimulus dan motivasi agar terpancing dan termotivasi untuk bertanya.
k. Peserta didik mengajukan pertanyaan berdasarkan hasil identifikasinya dalam memahami
masalah.

17. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :17/71
Fase 3: Data Collection (Pangumpulan Data)
a. Peserta didik diarahkan untuk memanfaatkan titik-titik koordinat objek dan bayangannya pada:
 Tabel 4.2 untuk menemukan matriks pencerminan terhadap cermin titik 𝑂(0,0).
 Tabel 4.3 untuk menemukan matriks pencerminan terhadap cermin sumbu 𝑥.
 Tabel 4.4 untuk menemukan matriks pencerminan terhadap cermin sumbu 𝑦.
 Tabel 4.5 untuk menemukan matriks pencerminan terhadap cermin garis 𝑦 = 𝑥.
 Tabel 4.6 untuk menemukan matriks pencerminan terhadap cermin garis 𝑦 = −𝑥.
b. Demonstrasikan proses menemukan (oleh pendidik pencerminan titik 𝑂(0,0) dan oleh peserta
didik pencerminan selanjutnya):
 Matriks pencerminan terhadap titik 𝑂(0,0) seperti pada buku siswa.
 Matriks pencerminan terhadap sumbu 𝑥 seperti pada buku siswa.
 Matriks pencerminan terhadap cermin sumbu 𝑦 seperti pada buku siswa.
 Matriks pencerminan terhadap cermin garis 𝑦 = 𝑥 seperti pada buku siswa.
 Matriks pencerminan terhadap cermin garis 𝑦 = −𝑥 seperti pada buku siswa.
c. Peserta didik diingatkan kembali tentang materi perkalian dan kesamaan dua matriks pada bab
sebelumnya.
d. Peserta didik dan pendidik bersama-sama membangun konsep:
 Pencerminan terhadap titik 𝑂(0,0)
Titik 𝐴(𝑥, 𝑦) dicerminkan terhadap titik 𝑂(0,0) menghasilkan bayangan 𝐴′(𝑥′,𝑦′) ditulis
dengan:
𝐴( 𝑥, 𝑦)
𝐶 𝑂(0,0)
→ 𝐴′( 𝑥′,𝑦′)atau (
𝑥′
𝑦′
) = (
−1 0
0 −1
) (
𝑥
𝑦)
 Pencerminan terhadap sumbu 𝑥
Titik 𝐴(𝑥, 𝑦) dicerminkan terhadap sumbu 𝑥 menghasilkan bayangan 𝐴′(𝑥′, 𝑦′) ditulis dengan:
𝐴( 𝑥, 𝑦)
𝐶𝑠𝑢𝑚𝑏𝑢 𝑥
→ 𝐴′( 𝑥′, 𝑦′)atau (
𝑥′
𝑦′
) = (
1 0
0 −1
)(
𝑥
𝑦)
 Pencerminan terhadap sumbu 𝑦
Titik 𝐴(𝑥, 𝑦) dicerminkan terhadap sumbu 𝑦 menghasilkan bayangan 𝐴′(𝑥′,𝑦′) ditulis dengan:
𝐴( 𝑥, 𝑦)
𝐶𝑠𝑢𝑚𝑏𝑢 𝑦
→ 𝐴′( 𝑥′,𝑦′)atau (
𝑥′
𝑦′) = (
−1 0
0 1
)(
𝑥
𝑦)
 Pencerminan terhadap garis 𝑥 = 𝑦
Titik 𝐴(𝑥, 𝑦) dicerminkan terhadap garis 𝑥 = 𝑦 menghasilkan bayangan 𝐴′(𝑥′,𝑦′) ditulis
dengan:
𝐴( 𝑥, 𝑦)
𝐶𝑠𝑢𝑚𝑏𝑢 𝑦
→ 𝐴′( 𝑥′,𝑦′)atau (
𝑥′
𝑦′
) = (
0 1
1 0
)(
𝑥
𝑦)
 Pencerminan terhadap garis 𝑦 = −𝑥
Titik 𝐴(𝑥, 𝑦) dicerminkan terhadap aris 𝑦 = −𝑥 menghasilkan bayangan 𝐴′(𝑥′,𝑦′) ditulis
dengan:
𝐴( 𝑥, 𝑦)
𝐶𝑠𝑢𝑚𝑏𝑢 𝑦
→ 𝐴′( 𝑥′,𝑦′)atau (
𝑥′
𝑦′
) = (
0 −1
−1 0
)(
𝑥
𝑦)

18. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :18/71
Fase 4: Data Processor (Pengelolahan Data)
a. Untuk mendapatkan tingkat pemahaman akan konsep pencerminan, peserta didik diarahkan
menyelesaikan masalah yang disajikan di LKPD (Kode 4b).
b. Peserta didik mencermati dan memahami masalah di LKPD.
c. Peserta didik menyusun informasi yang diperoleh dari hasil pengamatan.
d. Peserta didik diarahkan untuk memanfaatkan jenis-jenis pencerminan (refleksi) yang baru saja
dipelajari.
e. Peserta didik diharapkan dapat membentuk jejaring dengan berdiskusi dalam kelompoknya,
mengidentifikasi masalah dan menalar bagaimana cara menemukan solusi.
f. Peserta didik menuliskan informasi yang terdapat pada masalah tersebut secara teliti dengan
menggunakan bahasa sendiri yang mudah dipahami.
g. Peserta didik diarahkan untuk mencermati dan memahami:
 Contoh 4.3 dan contoh 4.4 untuk membantu menyelesaikan masalah pencerminan terhadap
cermin titik 𝑂(0,0).
 Contoh 4.5 dan contoh 4.6 untuk membantu menyelesaikan masalah pencerminan terhadap
cermin sumbu 𝑥.
 Contoh 4.7 dan contoh 4.8 untuk membantu menyelesaikan masalah pencerminan terhadap
cermin sumbu 𝑦.
 Contoh 4.9 dan contoh 4.10 untuk membantu menyelesaikan masalah pencerminan terhadap
cermin garis 𝑦 = 𝑥.
 Contoh 4.11 dan contoh 4.12 untuk membantu menyelesaikan masalah pencerminan terha-
dap cermin garis 𝑦 = −𝑥.
h. Kelompok yang melenceng dari pekerjaannya atau mengalami kesulitan dalam menyelesaikan
masalah diberi bimbingan langsung atau bimbingan secara klasikal.
i. Peserta didik mengingat kembali konsep persamaan garis dan sketsanya.
Fase 5: Verification (Pembuktian)
a. Satu kelompok dipilih secara acak untuk mempresentasikan hasil diskusinya.
b. Kelompok yang terpilih, selanjutnya bermusyawarah dengan hemat waktu untuk menentukan
seorang diantara mereka yang akan bertindak sebagai juri bicara.
c. Juru bicara yang terpilih menyajikan hasil diskusi kelompoknya di depan kelas dan anggota
kelompok yang tidak bertindak sebagai juru bicara dipersiapkan untuk menjawab tanggapan
ataupun pertanyaan dari kelompok lain.
d. Kelompok lain diberikan kesempatan untuk mengajukan pertanyaan mengenai hal-hal yang tidak
dipahami atau terdapat hal-hal yang berbeda antara hasil diskusi dalam kelompok dan presentasi
yang telah dilakukan oleh juru bicara.
e. Anggota kelompok penyaji (kecuali presenter) diberikan kesempatan untuk menanggapi atau
memberi respons terhadap pertanyaan yang masuk.
f. Melibatkan peserta didik untuk mengevaluasi jawaban kelompok penyaji serta masukan dari
peserta didik lain dan membuat kesepakatan, bila jawaban yang disampaikan sudah tepat.

19. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :19/71
3. Kegiatan Penutup (±15 menit):
Fase 6: Generalization (Menarik Kesimpulan/Generalisasi)
a. Peserta didik menalar dan membuat jejaring bersama pendidik dengan cara menyimpulkan dari
beberapa hasil presentasi tentang pencerminan (refleksi) dan bagaimana cara menyelesaikan
masalah yang terkait.
b. Memberi penegasan mengenai kesimpulan yang dikemukakan peserta didik.
c. Secara individu peserta didik melakukan refleksi (penilaian diri) tentang apa saja yang telah
dipelajari, mengidentifikasi manfaatnya, mengidentifikasi hal-hal yang sudah dan belum dipahami
untuk ditindak lanjuti.
d. Memberikan tugas.
e. Memberikan kuis.
f. Mengakhiri kegiatan belajar dan berpesan untuk mempelajari materi rotasi yang akan dibahas
pada pertemuan selanjutnya.
g. Bersama-sama dengan peserta didik berdoa untuk bersyukur kepada Allah SWT telah diberi
pengetahuan tentang pembelajaran yang telah dilakukan.
h. Mengakhiri pembelajaran dengan mengucapkan salam.
Rotasi (Pertemuan ......../..... JP)
1. Kegiatan Pendahuluan (±15 menit):
Orientasi
a. Melakukan pembukaan dengan mengucapkan salam pembuka.
b. Meminta ketua kelas untuk memimpin doa sebelum memulai pembelajaran.
c. Memeriksa kehadiran peserta didik sebagai sikap disiplin.
d. Menyiapkan fisik dan psikis peserta didik dalam mengawali kegiatan pembelajaran.
Fase 1: Stimulation (Stimulasi/Pemberian Rangsangan)
Motivasi
a. Memberikan gambaran tentang pentingnya memahami konsep rotasi, serta memberikan gam-
baran tentang penggunaannya dalam kehidupan sehari-hari.
b. Menyampaikan tujuan pembelajaran pada pertemuan yang berlangsung.
c. Mengajukan pertanyaan.
Apersepsi
a. Mengaitkan materi pembelajaran yang akan dilakukan dengan pengalaman peserta didik dengan
materi sebelumnya.
b. Mengingatkan kembali materi prasyarat dengan bertanya mengenai materi fungsi, trigonometri
dan matriks yang telah dipelajari di kelas X serta materi transformasi geometri (khususnya rotasi)
yang telah dipelajari di SMP.
c. Mengajukan pertanyaan yang ada keterkaitannya dengan pelajaran yang akan dilakukan.
 Informasikan kepada peserta didik bahwa konsep transformasi ini dikaji dengan pendekatan
koordinat dan hubungannya dengan konsep matriks.

20. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :20/71
 Memberikan beberapa contoh yang berkaitan dengan rotasi di kehidupan nyata:
 Kipas
 Roda
 Kincir Angin
 Mengarahkan peserta didik untuk memikirkan dan menyebutkan contah lain yang termasuk
rotasi.
 Berilah kesempatan kepada peserta didik untuk memikirkan posisi, bentuk dan ukuran objek
yang dirotasi tersebut.
 Informasikan kepada peserta didik bahwa pergerakan objek-objek tersebut akan dibahas
dengan pendekatan koordinat.
 Membuat asumsi dengan peserta didik, bahwa pergerakan ke arah sumbu 𝑥 positif adalah ke
kanan, pergerakan ke arah sumbu 𝑥 negatif adalah ke kiri, pergerakan ke arah sumbu 𝑦
positif adalah ke atas dan pergerakan ke arah sumbu 𝑦 negatif adalah ke bawah.
 Berdasarkan masalah dan kegiatan yang diberikan pada buku siswa, instruksikan peserta
didik agar mampu memahami materi rotasi.
Pemberian Acuan
a. Memberitahukan materi pelajaran yang akan dibahas pada pertemuan saat itu.
b. Memberitahukan tentang kompetensi inti, kompetensi dasar, indikator, dan KKM pada pertemuan
yang berlangsung.
c. Pembagian kelompok belajar.
d. Menjelaskan mekanisme pelaksanaan pengalaman belajar sesuai dengan langkah-langkah
pembelajaran.
2. Kegiatan Inti (±60 menit):
 Peserta didik bergabung bersama teman kelompoknya masing-masing dengan tertib dan hemat
waktu.
 Peserta didik mendapatkan motivasi agar tetap tekun, serius dan kompak dalam belajar.
 Peserta didik memperhatikan informasi yang disampaikan pendidik mengenai contoh-contoh
yang bergerak berputar di lingkungan sekitar (seperti kipas, kincir angin, roda dan lain-lain).
 Peserta didik diarahkan untuk memikirkan dan menyebutkan contoh lainnya yang termasuk
rotasi.
 Peserta didik diberikan motivasi untuk mempelajari konsep transformasi ketiga yaitu rotasi
dengan pendekatan koordinat dan kaitannya dengan konsep matriks.
Fase 2: Problem Statement (Pernyataan/Identifikasi Masalah)
a. Peserta didik berdiskusi secara berkelompok tentang masalah 4.4. dan diarahkan untuk
mengamati dan menalar perputaran segitiga jika titik pusat pemutaran berada pada bidang
segitiga, berada di salah satu sudut segitiga, dan berada diluar segitiga (lihat gambar 4.10 pada
buku siswa). Peserta didik memberi komentar mengenah hasil yang diperoleh dan diarahkan ke
sesi tanya jawab.

21. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :21/71
b. Peserta didik memperhatikan informasi bahwa gerak rotasi objek dipengaruhi oleh titik pusat
rotasi. Peserta didik diarahkan membandingkan kembali Gambar 4.10: A, B dan C.
c. Peserta didik melakukan pengamatann fokus pada bentuk, posisi dan ukuran objek sebelum dan
sesudah di rotasi.
d. Peserta didik diharapkan mengidentifikasi sebanyak mungkin pertanyaan yang berkaitan dengan
masalah yang diberikan.
e. Peserta didik diberikan stimulus agar terpancing dan termotivasi untuk bertanya.
f. Peserta didik mengajukan pertanyaan berdasarkan hasil identifikasinya memahami masalah.
Fase 3: Data Collection (Pangumpulan Data)
a. Peserta didik menemukan sifat rotasi berdasarkan pengamatan perputaran objek di lingkungan
sekitar pada bidang kartesius seperti pada Gambar 4.10 dan Gambar 4.11 di buku siswa. Sifat
yang ditemukan yakni bangun yang diputar (rotasi) tidak mengalami perubahan bentuk dan
ukuran.
b. Peserta didik memperhatikan demonstrasi pendidik mengenai proses menemukan matriks rotasi
pada pusat 𝑂(0,0) melalui Gambar 4.12 di buku siswa. Peserta didik mengingat kembali konsep
trigonometri serta kesamaan matriks.
c. Peserta didik diarahkan kembali melakukan percobaan untuk menemukan konsep rotasi pada
pusat 𝑃(𝑎, 𝑏) dengan melakukan: (1) translasi titik dengan 𝑇(−𝑎,−𝑏) sehingga pusat rotasi
menjadi 𝑂(0,0). Dengan demikian, matriks rotasi dengan pusat 𝑂(0,0) dapat digunakan,
kemudian (2) hasil rotasi pada langkah (1) ditranslasi kembali dengan 𝑇(𝑎, 𝑏).
d. Peserta didik bersama-sama menyimpulkan atau membangun konsep rotasi yang diputar dengan
sudut dan pusat 𝑃(𝑝, 𝑞).
Titik 𝐴(𝑥, 𝑦) diputar dengan pusat 𝑃(𝑝, 𝑞) dan sudut 𝛼 menghasilkan bayangan 𝐴′(𝑥′, 𝑦′) ditulis:
𝐴(𝑥, 𝑦)
𝑅[ 𝑃( 𝑝,𝑞),𝛼]
→ 𝐴′(𝑥′,𝑦′)
(
𝑥′
𝑦′
) = (
cos 𝛼 −sin 𝛼
sin 𝛼 cos 𝛼
) (
𝑥 − 𝑝
𝑦 − 𝑞) + (
𝑝
𝑞)
Fase 4: Data Processor (Pengelolahan Data)
a. Untuk mendapatkan tingkat pemahaman peserta didik mengenai konsep rotasi, peserta didik
menyelesaikan masalah yang disajikan di LKPD (Kode 4c).
b. Peserta didik mengamati masalah yang disajikan pada LKPD.
c. Peserta didik diarahkan untuk menerapkan materi rotasi yang baru saja dipelajari.
d. Peserta didik diharapkan dapat membentuk jejaring dengan berdiskusi dalam kelompoknya,
mengidentifikasi masalah dan menalar bagaimana cara menemukan solusi.
e. Peserta didik menuliskan informasi yang terdapat pada masalah tersebut secara teliti dengan
menggunakan bahasa sendiri yang mudah dipahami.
f. Kelompok yang melenceng dari pekerjannya atau mengalami kesulitan dalam menyelesaikan
masalah diberi bimbingan langsung atau bimbingan secara klasikal.
g. Peserta didik mencermati dan memahami contoh 4.13 dan contoh 4.14 pada buku siswa untuk
membantu menyelesaikan masalah di LKPD.

22. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :22/71
h. Masing-masing kelompok yang telah menemukan solusi yang diyakini tepat, selanjutnya menu-
liskan hasil yang diperoleh pada LKPD yang telah disediakan.
i. Peserta didik yang ditunjuk sebagai ketua dalam kelompoknya diingatkan untuk meyakinkan
bahwa tiap anggota telah mengetahui dan memahami masalah yang didiskusikan.
Fase 5: Verification (Pembuktian)
a. Satu kelompok dipilih secara acak untuk mempresentasikan hasil diskusinya secara sistematis
dengan bahasa yang sopan.
b. Kelompok yang terpilih, selanjutnya bermusyawarah dengan hemat waktu untuk menentukan
seorang diantara mereka yang akan bertindak sebagai juri bicara.
c. Juru bicara yang terpilih menyajikan hasil diskusi kelompoknya di depan kelas dan anggota
kelompok yang tidak bertindak sebagai juru bicara dipersiapkan untuk menjawab tanggapan
ataupun pertanyaan dari kelompok lain.
d. Kelompok lain diberikan kesempatan untuk mengajukan pertanyaan mengenai hal-hal yang tidak
dipahami atau terdapat hal-hal yang berbeda antara hasil diskusi dalam kelompok dan presentasi
yang telah dilakukan oleh juru bicara.
e. Anggota kelompok penyaji (kecuali presenter) diberikan kesempatan untuk menanggapi atau
memberi respons terhadap pertanyaan yang masuk.
f. Melibatkan peserta didik untuk mengevaluasi jawaban kelompok penyaji serta masukan dari
peserta didik lain dan membuat kesepakatan, bila jawaban yang disampaikan sudah tepat.
3. Kegiatan Penutup (±15 menit):
Fase 6: Generalization (Menarik Kesimpulan/Generalisasi)
a. Peserta didik menalar dan membuat jejaring bersama pendidik dengan cara menyimpulkan dari
beberapa hasil presentasi tentang pencerminan (refleksi) dan bagaimana cara menyelesaikan
masalah yang terkait.
b. Memberi penegasan mengenai kesimpulan yang dikemukakan peserta didik mengenai konsep
rotasi.
Penilaian diri
c. Secara individu peserta didik melakukan refleksi (penilaian diri) tentang apa saja yang telah
dipelajari, mengidentifikasi manfaatnya, mengidentifikasi hal-hal yang sudah dan belum dipahami
untuk ditindak lanjuti.
d. Memberikan tugas.
e. Memberikan kuis.
f. Mengakhiri kegiatan belajar dan berpesan untuk mempelajari materi dilatasi yang akan dibahas
pada pertemuan selanjutnya.
g. Bersama-sama dengan peserta didik berdoa untuk bersyukur kepada Allah SWT telah diberi
pengetahuan tentang pembelajaran yang telah dilakukan.
h. Mengakhiri pembelajaran dengan mengucapkan salam.

23. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :23/71
Dilatasi (Pertemuan ......../..... JP)
1. Kegiatan Pendahuluan (±15 menit):
Orientasi
a. Melakukan pembukaan dengan mengucapkan salam pembuka.
b. Meminta ketua kelas untuk memimpin doa sebelum memulai pembelajaran.
c. Memeriksa kehadiran peserta didik sebagai sikap disiplin.
d. Menyiapkan fisik dan psikis peserta didik dalam mengawali kegiatan pembelajaran.
Motivasi
a. Memberikan gambaran tentang pentingnya memahami konsep dilatasi, serta memberikan gam-
baran tentang penggunaannya dalam kehidupan sehari-hari
b. Menyampaikan tujuan pembelajaran pada pertemuan yang berlangsung.
c. Mengajukan pertanyaan.
Apersepsi
a. Mengaitkan materi pembelajaran yang akan dilakukan dengan pengalaman peserta didik dengan
materi sebelumnya.
b. Mengingatkan kembali materi prasyarat dengan bertanya mengenai materi fungsi, trigonometri
dan matriks serta materi transformasi geometri (khususnya dilatasi) yang telah dipelajari di SMP.
c. Mengajukan pertanyaan yang ada keterkaitannya dengan pelajaran yang akan dilakukan.
 Informasikan kepada peserta didik bahwa konsep transformasi ini dikaji dengan pendekatan
koordinat dan hubungannya dengan konsep matriks.
 Memberikan beberapa contoh yang berkaitan dengan dilatasi di kehidupan nyata:
Wilby dan teman-temannya berkunjung ke IPTN. Di sana, mereka mengamati miniatur
sebuah pesawat terbang. Miniatur pesawat terbang ini mempunyai bentuk yang sama
dengan pesawat terbang sesungguhnya, tetapi ukurannya lebih kecil. Bentuk seperti miniatur
pesawat terbang ini telah mengalami dilatasi diperkecil dari pesawat terbang sesungguhnya.
Selain dilatasi diperkecil, terdapat pula dilatasi diperbesar.
 Berilah kesempatan kepada peserta didik untuk memikirkan posisi, bentuk dan ukuran objek
yang mengalami dilatasi tersebut.
 Informasikan kepada peserta didik bahwa pergerakan objek-objek tersebut akan dibahas
dengan pendekatan koordinat.
 Berdasarkan masalah dan kegiatan yang diberikan pada buku siswa, instruksikan peserta
didik agar mampu memahami materi dilatasi.
Pemberian Acuan
a. Memberitahukan materi pelajaran yang akan dibahas pada pertemuan saat itu.
b. Memberitahukan tentang kompetensi inti, kompetensi dasar, indikator, dan KKM pada pertemuan
yang berlangsung.
c. Pembagian kelompok belajar.
d. Menjelaskan mekanisme pelaksanaan pengalaman belajar sesuai dengan langkah-langkah
pembelajaran.

24. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :24/71
2. Kegiatan Inti (±60 menit):
 Peserta didik bergabung bersama teman kelompoknya masing-masing dengan tertib dan hemat
waktu.
 Peserta didik mendapatkan motivasi agar tetap tekun, serius dan kompak dalam belajar.
 Peserta didik memberikan contoh dilatasi atau perkalian yang terjadi dalam kehidupan sehari-
hari. Peserta didik diarahkan memahami perkalian atau dilatasi dengan pendekatan koordinat.
Fase 1: Memahami Tantangan
Menggali Data
a. Peserta didik mengamati Masalah 4.5 pada buku siswa.
b. Peserta didik melakukan tanya-jawab dan mengomunikasikan pendapatnya akan Masalah 4.5
bersama teman kelompoknya masing-masing.
c. Peserta didik memahami Masalah 4.5 dan mengamati Gambar 4.13. Peserta didik diarahkan
untuk fokus mengamati pada jarak 𝑂𝐴 dengan 𝑂𝐴2 atau 𝑂𝐵 dengan 𝑂𝐵2 atau 𝑂𝐶 dengan 𝑂𝐶2.
Arahkan peserta didik kembali mengamati jarak 𝑂𝐴 dengan 𝑂𝐴1 atau 𝑂𝐵 dengan 𝑂𝐵1 atau 𝑂𝐶
dengan 𝑂𝐶1.
d. Peserta didik diberikan kesempatan untuk berdiskusi.
e. Satu kelompok dipilih secara acak untuk mengomunikasikan pendapat mereka “apa itu dilatasi?”.
f. Peserta didik secara berkelompok membuat contoh lain mengenai dilatasi titik, garis dan bidang
secara gambar. Kemudian menyajikannya di depan kelas.
g. Peserta didik menjawab pertanyaan yakni: yang manakah pusat dilatasi dan faktor skala dilatasi
pada Gambar 4.13?
h. Peserta didik diarahkan untuk konsentrasi pada ukuran objek dengan dilatasinya. Peserta didik
memperhatikan ukuran, ukuran dilatasinya dengan faktor skala dilatasi.
i. Seorang peserta didik dipilih secara acak untuk menyampaikan pendapatnya.
j. Peserta didik diarahkan untuk bernalar dan memberikan komentar atau pendapatnya kembali
akan gambar dengan dilatasi 𝑘, dimana 𝑘 > 0, 𝑘 = 0 dan k < 0.
k. Melalui kegiatan pengamatan pada contoh-contoh perkalian (dilatasi) dilingkungan sekitar dan
pengamatan dilatasi objek pada bidang koordinat maka peserta didik diarahkan untuk memahami
sifat 4.4.
l. Peserta didik mengamati Gambar 4.14 dengan konsentrasi pada pusat dilatasi setiap objek
(𝐴, 𝐵, 𝐶, 𝐷 dan E).
m. Peserta didik mengamati koordinat objek tersebut, koordinat hasil dilatasi, koordinat pusat
dilatasi serta jarak objek ke pusat dilatasi dan jarak hasil dilatasi ke pusat dilatasi.
n. Peserta didik melengkapi Tabel 4.7 dengan melihat panduan pada sel yang telah terisi. Peserta
didik diarahkan melengkapi sel. Tabel 4.7 telah terisi sebagai berikut:
No. Pusat Obyek Hasil Pola
1 2 3 4 5
1 𝑃(0,0) 𝐴(2,2) 𝐴′(6,6) (
6
6
) = 3((
2
2
) − (
0
0
)) + (
0
0
)

25. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :25/71
No. Pusat Obyek Hasil Pola
1 2 3 4 5
2 𝑃(0,0) 𝐵(−2,2) 𝐵′(2,−2) (
2
−2
) = −1((
−2
2
) − (
0
0
)) + (
0
0
)
3 𝑃(9,0) 𝐶(9,2) 𝐶′(9,−4) (
9
−4
) = −2((
9
2
) − (
9
0
)) + (
9
0
)
4 𝑃(−10,1) 𝐷(−8,2) 𝐷′(−2,5) (
−2
5
) = 4((
−8
2
) − (
−10
1
)) + (
−10
1
)
5 𝑃(−8, −3) 𝐸(−7,−3) 𝐸′(−3,−3) (
−3
−3
) = 5((
−7
−3
) − (
−8
−3
)) + (
−8
−3
)
o. Peserta didik mengamati dan menganalisis pola perhitungan pada tabel 4.7 dengan melihat
kolom 5.
p. Berdasarkan pengamatan dan bentuk pola yang ditemukan, peserta didik diarahkan menuliskan
konsep dilatasi dengan pusat 𝑃(𝑝, 𝑞) dan skala 𝑘.
Titik 𝐴(𝑥, 𝑦) dilatasi dengan pusat 𝑃(𝑝, 𝑞) dan skala 𝑘 menghasilkan bayangan 𝐴′(𝑥′,𝑦′), ditulis:
𝐴(𝑥, 𝑦)
𝑅[ 𝑃( 𝑝,𝑞),𝑘]
→ 𝐴′(𝑥′,𝑦′)
(
𝑥′
𝑦′
) = 𝑘 (
𝑥 − 𝑝
𝑦 − 𝑞) + (
𝑝
𝑞)
Merumuskan Masalah
a. Untuk mendapatkan tingkat pemahaman peserta didik akan konsep dilatasi, peserta didik men-
yelesaikan masalah yang disajikan di LKPD (Kode 4d).
b. Peserta didik mengingat kembali konsep dilatasi yang telah dipelajari sebelumnya.
c. Peserta didik memperhatikan penjelasan mengenai informasi masalah yang akan diamati.
d. Peserta didik mengamati dan mencermati masalah.
e. Peserta didik diberikan kesempatan untuk mengidentifikasi permasalahan.
f. Peserta didik memperoleh gambaran mengenai masalah yang telah dirumuskan dengan diskusi
dan tanya jawab.
g. Peserta didik mendapatkan stimulus dengan cara memberikan pertanyaan yang memerlukan
analisis, misalnya bagaimana cara menentukan dilatasi suatu garis lurus atau parabola (masalah
LKPD).
h. Peserta didik menanya atau mendiskusikan (antar peserta didik dalam satu kelompok atau diluar
kelompok, dan/atau pendidik) tentang masalah yang diamati.
Fase 2: Membangkitkan Gagasan
a. Peserta didik diberikan waktu dan kesempatan untuk mengungkapkan gagasan dan membentuk
jejaring dengan cara diskusi kelompok serta membimbimbing peserta didik untuk menyepakati
alternatif pemecahan yang akan di uji.
b. Memastikan kelompok dapat bekerja sama, terlibat aktif dalam merumuskan solusi yang akan
dicapai dengan menstimulasi peserta didik untuk bertanya.
c. Peserta didik menuliskan informasi yang terdapat pada masalah tersebut secara teliti dengan
menggunakan bahasa sendiri yang mudah dipahami.

26. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :26/71
d. Kelompok yang melenceng dari pekerjaannya atau mengalami kesulitan dalam menyelesaikan
masalah diberi bimbingan langsung atau bimbingan secara klasikal.
Fase 3: Mempersiapkan Tindakan
Mengembangkan Solusi
a. Peserta didik mengumpulkan informasi yang sesuai dari berbagai sumber belajar yang tersedia.
b. Peserta didik mengidentifikasi masalah dan menalar bagaimana cara menemukan solusi.
c. Peserta didik mengamati contoh 4.15 dan contoh 4.16 beserta alternatif penyelesaiannya pada
buku siswa sebagai informasi tambahan untuk menyelesaikan masalah pada LKPD (Kode 4d).
d. Kelompok yang telah menemukan penyelesaian masalahnya diinstruksikan untuk memeriksa
kembali secara detail solusi yang diperoleh.
e. Peserta didik yang ditunjuk sebagai ketua dalam kelompoknya diingatkan untuk meyakinkan
bahwa tiap anggota telah mengetahui dan memahami masalah yang didiskusikan.
f. Masing-masing kelompok yang telah menemukan solusi yang diyakini tepat, selanjutnya menu-
liskan hasil yang diperoleh pada LKPD yang telah disediakan.
Membangun Penerimaan
a. Satu kelompok dipilih secara acak untuk mempresentasikan hasil diskusinya.
b. Kelompok yang terpilih, selanjutnya bermusyawarah dengan hemat waktu untuk menentukan
seorang diantara mereka yang akan bertindak sebagai juri bicara.
c. Juru bicara yang terpilih menyajikan hasil diskusi kelompoknya di depan kelas dan anggota
kelompok yang tidak bertindak sebagai juru bicara dipersiapkan untuk menjawab tanggapan
ataupun pertanyaan dari kelompok lain.
d. Kelompok lain diberikan kesempatan untuk mengajukan pertanyaan mengenai hal-hal yang tidak
dipahami atau terdapat hal-hal yang berbeda antara hasil diskusi dalam kelompok dan presentasi
yang telah dilakukan oleh juru bicara.
e. Anggota kelompok penyaji (kecuali presenter) diberikan kesempatan untuk menanggapi atau
memberi respons terhadap pertanyaan yang masuk.
f. Melibatkan peserta didik untuk mengevaluasi jawaban kelompok penyaji serta masukan dari
peserta didik lain dan membuat kesepakatan, bila jawaban yang disampaikan sudah tepat.
3. Kegiatan Penutup (±15 menit):
a. Peserta didik diminta menyimpulkan konsep dilatasi.
b. Memberi penegasan mengenai kesimpulan yang dikemukakan peserta didik.
c. Secara individu peserta didik melakukan refleksi (penilaian diri) tentang apa saja yang telah
dipelajari, mengidentifikasi manfaatnya, mengidentifikasi hal-hal yang sudah dan belum dipahami
untuk ditindak lanjuti.
d. Memberikan tugas.
e. Memberikan kuis.
f. Mengakhiri kegiatan belajar dan berpesan untuk mempelajari materi transformasi yang akan
dibahas pada pertemuan selanjutnya.

27. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :27/71
g. Bersama-sama dengan peserta didik berdoa untuk bersyukur kepada Allah SWT telah diberi
pengetahuan tentang pembelajaran yang telah dilakukan.
h. Mengakhiri pembelajaran dengan mengucapkan salam.
Komposisi Transformasi (Pertemuan ......../..... JP)
1. Kegiatan Pendahuluan (±15 menit):
Orientasi
a. Melakukan pembukaan dengan mengucapkan salam pembuka.
b. Meminta ketua kelas untuk memimpin doa sebelum memulai pembelajaran.
c. Memeriksa kehadiran peserta didik sebagai sikap disiplin.
d. Menyiapkan fisik dan psikis peserta didik dalam mengawali kegiatan pembelajaran.
Fase 1: Menyampaikan Tujuan dan Mempersiapkan Peserta Didik
Motivasi
a. Memberikan gambaran tentang pentingnya memahami konsep komposisi transformasi, serta
memberikan gambaran tentang penggunaannya dalam kehidupan sehari-hari.
b. Menyampaikan tujuan pembelajaran pada pertemuan yang berlangsung.
c. Mengajukan pertanyaan.
Apersepsi
a. Mengaitkan materi pembelajaran yang akan dilakukan dengan pengalaman peserta didik dengan
materi sebelumnya.
b. Mengingatkan kembali materi prasyarat dengan bertanya mengenai materi komposisi fungsi,
trigonometri dan matriks yang telah dipelajari di kelas X.
c. Menyampaikan informasi yang ada keterkaitannya dengan pelajaran yang akan dilakukan.
 Informasikan kepada peserta didik bahwa konsep komposisi transformasi ini dikaji dengan
pendekatan koordinat dan hubungannya dengan konsep matriks.
 Instruksikan peserta didik agar mampu memahami materi komposisi transformasi.
Pemberian Acuan
a. Memberitahukan materi pelajaran yang akan dibahas pada pertemuan saat itu.
b. Memberitahukan tentang kompetensi inti, kompetensi dasar, indikator, dan KKM pada pertemuan
yang berlangsung.
c. Pembagian kelompok belajar.
d. Menjelaskan mekanisme pelaksanaan pengalaman belajar sesuai dengan langkah-langkah
pembelajaran.
2. Kegiatan Inti (±60 menit):
 Peserta didik bergabung bersama teman kelompoknya dengan tertib dan hemat waktu.
 Peserta didik memberikan contoh komposisi transformasi yang terjadi dalam kehidupan sehari-
hari. Peserta didik diarahkan memahami komposisi transformasi dengan pendekatan koordinat
dan hubungannya dengan konsep matriks.

28. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :28/71
Fase 2: Mendemonstrasikan Keterampilan atau Mempresentasikan Pengetahuan
a. Peserta didik mengingat kembali konsep transformasi (translasi, refleksi, rotasi dan dilatasi)
secara umum.
b. Peserta didik memperhatikan dengan saksama demonstrasi yang dilakukan oleh pendidik
mengenai materi komposisi transformasi secara singkat, padat dan jelas, diantaranya:
 Komposisi Translasi.
 Komposisi Refleksi.
 Komposisi Rotasi
 Komposisi Dilatasi.
Fase 3: Membimbing Pelatihan
a. Peserta didik mengamati dan memahami:
 Masalah 4.6 untuk komposisi translasi.
 Masalah 4.7 untuk komposisi refleksi.
 Masalah 4.8 untuk komposisi rotasi.
 Masalah 4.9 untuk komposisi dilatasi
b. Peserta didik dipandu untuk mengamati dan menalar bentuk pergeseran, pencerminan,
perputaran dan perkalian yang diceritakan pada masalah tersebut.
c. Peserta didik memberi komentar atau pendapat terhadap hasil pengamatan yang dilakukan dan
mengarahkannya ke sesi tanya-jawab.
d. Peserta didik dituntun memahami konsep komposisi translasi, refleksi, rotasi dan dilatasi secara
umum. Peserta didik memperhatikan informasi bahwa konsep ini sama halnya dengan komposisi
fungsi pada umumnya atau konsep komposisi yang telah dipelajari lebih awal.
e. Peserta didik diarahkan memahami perbedaan antara komposisi translasi, refleksi, rotasi dan
dilatasi. Peserta didik memberikan komentar tentang perbedaan keempat komposisi transformasi
tersebut.
f. Peserta didik diarahkan untuk fokus pada proses translasi, refleksi, rotasi dan dilatasi bertahap
sehingga terbentuk komposisi translasi, refleksi, rotasi dan dilatasi.
g. Peserta didik secara bersama-sama dituntun oleh pendidik untuk menemukan konsep komposisi
translasi, refleksi, rotasi dan dilatasi.
h. Peserta didik memberikan pendapat tentang:
 Skema 4.1 untuk komposisi translasi.
 Skema 4.2 untuk komposisi refleksi.
 Skema 4.3 untuk komposisi rotasi.
 Skema 4.4 untuk komposisi dilatasi.
Fase 4: Mengecek Pemahaman dan Memberikan Umpan Balik
a. Untuk mengecek tingkat pemahaman mengenai komposisi transformasi maka peserta didik
secara berkelompok mengerjakan LKPD (Kode 4e).
b. Peserta didik memperoleh motivasi agar terlibat aktif dalam memecahkan masalah.
c. Peserta didik memperhatikan penjelasan informasi mengenai masalah yang akan diamati.

29. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :29/71
d. Peserta didik mengamati dan mencermati masalah.
e. Peserta didik menuliskan informasi yang diperoleh dari hasil mengamati masalah.
f. Peserta didik diberikan stimulus dengan cara memberikan pertanyaan yang memerlukan analisis,
misalnya apakah ada syarat tertentu mengenai entri matriks dari segi susunan dan sifatnya.
g. Peserta didik menanya atau mendiskusikan (antar peserta didik dalam satu kelompok atau diluar
kelompok, dan/atau pendidik) tentang masalah yang diamati.
h. Peserta didik berdiskusi kelompok untuk menyelesaikan masalah.
i. Setiap kelompok diberikan kesempatan untuk mengamati, berpikir, dan bertanya berkaitan
dengan materi yang diberikan.
j. Peserta didik mengamati:
 Contoh 4.17 untuk membantu menyelesaikan masalah komposisi translasi.
 Contoh 4.18 untuk membantu menyelesaikan masalah komposisi refleksi.
 Contoh 4.19 dan contoh 4.20 untuk membantu menyelesaikan masalah komposisi rotasi.
 Contoh 4.21 untuk membantu menyelesaikan masalah komposisi dilatasi.
k. Peserta didik diminta memanfaatkan semua sumber belajar yang dimiliki (termasuk buku atau
literatur lain yang berkaitan dengan masalah).
l. Kelompok yang mengalami kesulitan diberi bimbingan langsung atau bimbingan secara klasikal.
m. Kelompok yang telah menemukan penyelesaian masalahnya diinstruksikan untuk memeriksa
kembali secara detail solusi yang diperoleh.
n. Peserta didik yang ditunjuk sebagai ketua dalam kelompoknya diingatkan untuk meyakinkan
bahwa tiap anggota telah mengetahui dan memahami masalah yang didiskusikan.
Fase 5: Memberikan Kesempatan untuk Pelatihan Lanjutan dan Penerapan
a. Satu kelompok dipilih secara acak untuk mempresentasikan hasil diskusinya.
b. Kelompok yang terpilih, selanjutnya bermusyawarah dengan hemat waktu untuk menentukan
seorang diantara mereka yang akan bertindak sebagai juri bicara.
c. Juru bicara yang terpilih menyajikan hasil diskusi kelompoknya di depan kelas dan anggota
kelompok yang tidak bertindak sebagai juru bicara dipersiapkan untuk menjawab tanggapan
ataupun pertanyaan dari kelompok lain.
d. Kelompok lain diberikan kesempatan untuk mengajukan pertanyaan mengenai hal-hal yang tidak
dipahami atau terdapat hal-hal yang berbeda antara hasil diskusi dalam kelompok dan presentasi
yang telah dilakukan oleh juru bicara.
e. Anggota kelompok penyaji (kecuali presenter) diberikan kesempatan untuk menanggapi atau
memberi respons terhadap pertanyaan yang masuk.
f. Pendidik menjadi fasilitator dan menjaga keadaan kelas tetap terarah pada pembelajaran.
g. Pendidik mengamati kebenaran jawaban dan konsep.
h. Pendidik melakukan penilaian.
i. Peserta didik dilibatkan untuk mengevaluasi jawaban kelompok penyaji serta masukan dari
peserta didik lain dan membuat kesepakatan, bila jawaban yang disampaikan sudah tepat.
j. Peserta didik mengerjakan latihan lanjutan: uji kompetensi 4.3 nomor 7 s.d. 10 pada buku siswa.

30. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :30/71
3. Kegiatan Penutup (±15 menit):
a. Peserta didik diminta menyimpulkan konsep komposisi transformasi (translasi, refleksi, rotasi dan
dilatasi) dengan bahasa sendiri:
b. Memberi penegasan tentang kesimpulan yang telah disampaikan peserta didik.
c. Secara individu peserta didik melakukan refleksi (penilaian diri) tentang apa saja yang telah
dipelajari, mengidentifikasi manfaatnya, mengidentifikasi hal-hal yang sudah dan belum dipahami
untuk ditindak lanjuti.
d. Memberikan tugas.
e. Mengakhiri kegiatan belajar dan berpesan untuk mempelajari materi barisan aritmetika dan
barisan geometri yang akan dibahas pada pertemuan selanjutnya.
f. Pendidik bersama-sama dengan peserta didik berdoa untuk bersyukur kepada Allah SWT telah
diberi pengetahuan tentang pembelajaran yang telah dilakukan.
g. Mengakhiri pembelajaran dengan mengucapkan salam.
I. Penilaian Hasil Pembelajaran :
1. Teknik Penilaian: melalui pengamatan dan tes tertulis
2. Prosedur Penilaian:
No Aspek yang Dinilai
Teknik
Penilaian
Waktu
Penilaian
1 Ketrampilan:
1. Terampil menemukan matriks transformasi
(translasi, refleksi, rotasi, dan dilatasi) dengan
pengamatan terhadap titik-titik dan bayangannya.
2. Terampil menggunakan konsep transformasi
(translasi, refleksi, rotasi, dan dilatasi) dengan
kaitannya dengan konsep matriks dalam
menemukan koordinat titik atau fungsi setelah
ditransformasi.
3. Terampil membandingkan proses transformasi
(translasi, refleksi, rotasi, dan dilatasi).
Pengamatan
Penyelesaian
kelompok dan
saat diskusi
2 Pengetahuan:
1. Menyebutkan contoh translasi, refleksi, rotasi, dan
dilatasi dalam kehidupan sehari-hari.
2. Menemukan sifat-sifat translasi, refleksi, rotasi,
dan dilatasi berdasarkan pengamatan pada
masalah kontekstual dan pengamatan objek pada
bidang koordinat.
3. Menemukan konsep translasi dengan kaitannya
dengan konsep matriks.
Tes tertulis
dan
Lisan
Penyelesaian
tugas
kelompok

31. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :31/71
No Aspek yang Dinilai
Teknik
Penilaian
Waktu
Penilaian
4. Menemukan konsep refleksi terhadap titik 𝑂(0,0)
dengan kaitannya dengan konsep matriks.
5. Menemukan konsep refleksi terhadap sumbu x
dengan kaitannya dengan konsep matriks.
6. Menemukan konsep refleksi terhadap sumbu y
dengan kaitannya dengan konsep matriks.
7. Menemukan konsep refleksi terhadap garis 𝑦 = 𝑥
dengan kaitannya dengan konsep matriks.
8. Menemukan konsep refleksi terhadap garis 𝑦 =
−𝑥 dengan kaitannya dengan konsep matriks.
9. Menemukan konsep rotasi pada suatu sudut dan
pusat 𝑂(0,0) dengan kaitannya dengan konsep
matriks.
10. Menemukan konsep rotasi pada suatu sudut dan
pusat 𝑃(𝑝, 𝑞) dengan kaitannya dengan konsep
matriks.
11. Menemukan konsep dilatasi pada faktor skala 𝑘
dan pusat 𝑂(0,0) dengan kaitannya dengan
konsep matriks.
12. Menemukan konsep dilatasi pada faktor skala 𝑘
dan pusat 𝑃(𝑝, 𝑞) dengan kaitannya dengan
konsep matriks.
13. Membandingkan keempat jenis transformasi
dengan menyebutkan perbedaannya.
14. Menemukan konsep komposisi transformasi
(translasi, refleksi, rotasi, dan dilatasi).
3. Instrumen Penilaian
a. Ketrampilan : Terlampir.
b. Pengetahuan : Terlampir.
Ujung, ........................................
Guru Mata Pelajaran,
MUH. ALFIANSYAH, S.Pd., M.Pd.

32. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :32/71
Lampiran A
Instrumen Penilaian Keterampilan
LEMBAR PENGAMATAN PENILAIAN KETERAMPILAN
Mata Pelajaran : Matematika
Materi : Transformasi
Kelas/Semester : XI/Ganjil
Tahun Pelajaran : ................................
Waktu Pengamatan : Penyelesaian Tugas Kelompok dan Saat Diskusi
No. Nama Peserta Didik
Skor Keterampilan
Jumlah NilaiMenemukan
matriks
transformasi
Menggunakan
matriks
transformasi
Membandingkan
proses
transformasi

33. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :33/71
Indikator terampil menemukan matriks transformasi.
1. Kurang terampil jika sama sekali tidak dapat menemukan matriks transformasi.
2. Cukup terampil jika menunjukkan mampu menemukan dua atau satu matriks transformasi.
3. Terampil, jika menunjukkan mampu menemukan tiga matriks transformasi.
4. Sangat terampil, jika menunjukkan mampu menemukan keempat matriks transformasi.
Indikator terampil menggunakan matriks transformasi.
1. Kurang terampil jika sama sekali tidak dapat menggunakan matriks transformasi.
2. Cukup terampil jika menunjukkan mampu menggunakan dua atau satu matriks transformasi.
3. Terampil, jika menunjukkan mampu menggunakan tiga matriks transformasi.
4. Sangat terampil, jika menunjukkan mampu menggunakan keempat matriks transformasi.
Indikator terampil membandingkan matriks transformasi.
1. Kurang terampil jika sama sekali tidak dapat membandingkan matriks transformasi.
2. Cukup terampil jika menunjukkan mampu membandingkan dua matriks transformasi.
3. Terampil, jika menunjukkan mampu membandingkan tiga matriks transformasi.
4. Sangat terampil, jika menunjukkan mampu membandingkan keempat matriks transformasi.

34. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :34/71
Lampiran B
Instrumen Penilaian Pengetahuan
TEKNIK TES TERTULIS
Satuan Pendidikan : MA Pondok Pesantren Al-Ikhlas Bone
Mata Pelajaran : Matematika
Kelas/Semester : XI/Ganjil
Kompetensi Dasar : 3.5. Menganalisis dan membandingkan transformasi dan komposisi trans-
formasi dengan menggunakan matriks.
Indikator : 3.5.1 Menyebutkan contoh translasi, refleksi, rotasi, dan dilatasi dalam
kehidupan sehari-hari.
3.5.2 Menemukan sifat-sifat translasi, refleksi, rotasi, dan dilatasi
berdasarkan pengamatan pada masalah kontekstual dan pengamatan
objek pada bidang koordinat.
3.5.3 Menemukan konsep translasi dengan kaitannya dengan konsep
matriks.
3.5.4 Menemukan konsep refleksi terhadap titik 𝑂(0,0) dengan kaitannya
dengan konsep matriks.
3.5.5 Menemukan konsep refleksi terhadap sumbu x dengan kaitannya
dengan konsep matriks.
3.5.6 Menemukan konsep refleksi terhadap sumbu y dengan kaitannya
dengan konsep matriks.
3.5.7 Menemukan konsep refleksi terhadap garis 𝑦 = 𝑥 dengan kaitannya
dengan konsep matriks.
3.5.8 Menemukan konsep refleksi terhadap garis 𝑦 = −𝑥 dengan kaitannya
dengan konsep matriks.
3.5.9 Menemukan konsep rotasi pada suatu sudut dan pusat 𝑂(0,0) dengan
kaitannya dengan konsep matriks.
3.5.10 Menemukan konsep rotasi pada suatu sudut dan pusat 𝑃(𝑝, 𝑞) dengan
kaitannya dengan konsep matriks.
3.5.11 Menemukan konsep dilatasi pada faktor skala 𝑘 dan pusat 𝑂(0,0)
dengan kaitannya dengan konsep matriks.
3.5.12 Menemukan konsep dilatasi pada faktor skala 𝑘 dan pusat 𝑃(𝑝, 𝑞)
dengan kaitannya dengan konsep matriks.
3.5.13 Membandingkan keempat jenis transformasi dengan menyebutkan
perbedaannya.
3.5.14 Menemukan konsep komposisi transformasi (translasi, refleksi, rotasi,
dan dilatasi).
Materi : Transformasi
Petunjuk:
1. Kerjakan soal berikut secara individu, dilarang bekerja sama dan dilarang menyontek.
2. Selesaikanlah soal-soal berikut ini.
A. Translasi (Pertemuan...............................)
1. Tunjukanlah secara gambar pergeseran titik 𝑃(3, −5) bila digeser 3 satuan ke kanan dan 4
satuan ke bawah dari beberapa titik berikut! Asumsikan arah ke kanan adalah sumbu x positif
dan arah ke atas adalah ke arah y positif

35. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :35/71
2. Suatu segitiga sebarang dengan titik-titik sudut 𝐴(1, 1), 𝐵(3,3), 𝐶(5,2) di translasikan dengan 𝑇 =
(
−3
2
). Tentukan kedudukan akhir dari segitiga serta gambarkan dalam koordinat kartesisus!
B. Refleksi (Pertemuan...............................)
1. Tunjukkanlah secara gambar pencerminan titik 𝐴(2, −3) bila dicerminkan terhadap sumbu 𝑥.
2. Tentukanlah persamaan kurva oleh pencerminan garis lurus 2𝑥 − 3𝑦 + 4 = 0 dicerminkan
terhadap garis 𝑦 = 𝑥.
C. Rotasi (Pertemuan...............................)
1. Tunjukkan secara gambar perputaran titik 𝐴(2,−3) dirotasi sebesar 90° dengan pusat rotasi
𝑂(0,0)!
2. Tentukan persamaan kurva oleh rotasi R berikut!
Garis lurus 2𝑥 − 3𝑦 + 4 = 0 dirotasi sebesar 90° dengan pusat rotasi 𝑂(0,0)!
D. Dilatasi (Pertemuan...............................)
1. Tunjukkan secara gambar titik 𝐴(2,3) didilatasikan dengan skala 2 dengan pusat 𝑂(0,0)!
2. Gambarkanlah segitiga 𝐴𝐵𝐶 dengan koordinat 𝐴(−2,0), 𝐵(2,0) 𝑑𝑎𝑛 𝐶(2,3) bila didilitasikan
dengan faktor skala 3 dengan pusat 𝑃(1,1).

36. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :36/71
ALTERNATIF PENYELESAIAN
TEKNIK TES TERTULIS
A. Translasi
1. Titik 𝑃(3, −5) ditranslasikan terhadap
𝑇(3, −4)
𝑃 (
𝑥
𝑦)
𝑇 ( 𝑎
𝑏
)
→ 𝑃 (
𝑥 + 𝑎
𝑦 + 𝑏)
𝑃 (
3
−5
)
𝑇 ( 3
−4
)
→ 𝑃 (
3 + 3
−5 + (−4)
)
𝑃′(3 + 3,−5 + (−4))
𝑃′(6,−9)
Sketsa Gambar
2. 𝐴 (1,1)
𝑇 (−3
2
)
→ 𝐴′(−2,3)
𝐵 (3,3)
𝑇 (−3
2
)
→ 𝐴′(0,5)
𝐴 (5,2)
𝑇 (−3
2
)
→ 𝐴′(2,4)
Sketsa Gambar
B. Refleksi
1. 𝐴 (
𝑎
𝑏
)
𝑅 𝑠𝑢𝑚𝑏𝑢 𝑥
→ 𝐴 (
𝑎
−𝑏
)
(
𝑎
−𝑏
) = (
1 0
0 −1
) (
2
−3
)
(
𝑎
−𝑏
) = (
2
3
)
Maka kedudukan titik 𝐴′ adalah (
2
3
)
Sketsa Gambar
2. 𝑃 (
𝑥
𝑦)
𝑅 𝑦=−𝑥
→ 𝑃′(
𝑥′
𝑦′
)
𝑃′ (
𝑥′
𝑦′ ) = (
0 −1
−1 0
) (
𝑥
𝑦) = (
−𝑦
−𝑥
)
Diperoleh 𝑥′ = −𝑦 atau 𝑦 = −𝑥′
Serta 𝑦′ = −𝑥 atau 𝑥 = −𝑦′
Maka diperoleh bayangan garis lurus dengan
persamaan:
2(−𝑦′)− 3(−𝑥′)+ 4 = 0
−2𝑦 + 3𝑥 + 4 = 0
Dengan demikian, bayangan 2𝑥 − 3𝑦 + 4 = 0
setelah dicerminkan terhadap garis 𝑦 = −𝑥
adalah 3𝑥 − 2𝑦 + 4 = 0.

37. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :37/71
C. Rotasi
1. (
𝑥′
𝑦′
) = (
cos90 −sin 90
sin 90 cos90
) (
2
−3
)
(
𝑥′
𝑦′
) = (
0 −1
1 0
) (
2
−3
)
(
𝑥′
𝑦′
) = (
2
3
)
Maka kedudukan titik 𝐴′ adalah (3,2)
Sketsa Gambar
2. (
𝑥′
𝑦′) = (
0 −1
1 0
) (
𝑥
𝑦) = (
−𝑦
𝑥
)
Diperoleh 𝑥′ = −𝑦 atau 𝑦 = −𝑥′
Serta 𝑦′ = 𝑥 atau 𝑥 = 𝑦′
Sehingga dengan mensubtitusikan ke
persamaan garis lurus maka diperoleh
bayangan garis lurus dengan persamaan:
2( 𝑦′) − 3(−𝑥′)+ 4 = 0
2𝑦 + 3𝑥 + 4 = 0
Dengan demikian, bayangan 2𝑥 − 3𝑦 + 4 = 0
setelah dirotasikan 90° dengan pusat rotasi
𝑂(0,0)adalah 3𝑥 + 2𝑦 + 4 = 0.
D. Dilatasi
1. (
𝑥′
𝑦′
) = (
𝑘 0
0 𝑘
) (
𝑥
𝑦)
(
𝑥′
𝑦′
) = (
2 0
0 2
) (
2
3
)
(
𝑥′
𝑦′
) = (
4
6
)
Maka kedudukan titik 𝐴′ adalah (4,6)
Sketsa Gambar
2. Untuk titik 𝐴(−2,0)
(
𝑥′
𝑦′
) = 3(
−2 − 1
0 − 1
) + (
1
1
) = (
−8
−2
)
Maka 𝐴′nya adalah (−8,−2).
Untuk titik 𝐵(2,0)
(
𝑥′
𝑦′
) = 3(
2 − 1
0 − 1
) + (
1
1
) = (
4
−2
)
Maka 𝐴′nya adalah (−8,−2)
Untuk titik 𝐶(2,3)
(
𝑥′
𝑦′
) = 3(
2 − 1
3 − 1
) + (
1
1
) = (
4
7
)
Maka 𝐴′nya adalah (4,7)

38. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :38/71
RUBRIK PENILAIAN TES TERTULIS
Translasi, Refleksi, Rotasi dan Dilatasi (Pertemuan .....................)
No. Aspek Penilaian Rubrik Penilaian Skor Skor Maksimal
1 Pemahaman
terhadap konsep
transformasi
Penyelesaian dihubungkan dengan konsep
transformasi.
5
5
Sudah menghubungkan penyelesaian dengan
konsep transformasi namun belum benar.
3
Penyelesaian sama sekali tidak dihubungkan
dengan konsep transformasi.
1
Tidak ada respons jawaban. 0
2 Kebanaran
jawaban akhir soal
Jawaban benar 5
5
Jawaban hampir benar 3
Jawaban salah 1
Tidak ada respons jawaban 0
3 Proses
perhitungan
Proses perhitungan benar 5
5
Proses perhitungan sebagian besar benar 3
Proses perhitungan sebgaian kecil saja yang
benar
2
Proses perhitungan sama sekali salah 1
Tidak ada respons jawaban 0
4 Membuat Sketsa Sketsa objek dan bayangan oleh transformasi
benar.
5
5
Sketsa objek dan bayangan oleh transformasi
benar, tapi kurang lengkap.
3
Sketsa objek dan bayangan oleh transformasi
tidak benar.
1
Tidak ada sketsa 0
Skor Maksimal 20
Skor Minimal 0
Catatan:
Untuk Translasi dan Dilatasi
 Rubrik yang digunakan sama untuk dua butir soal, sedemikian sehingga Skor Maksimal untuk kedua
butir soal adalah 40.
Untuk Refleksi dan Rotasi
 Butir soal pertama dinilai lengkap dari empat aspek sehingga skor maksimalnya 20.
 Butir soal kedua hanya dinilai dari tiga aspek (kecuali aspek ke-4: membuat sketsa) sehingga skor
maksimalnya 15.
 Jadi skor total untuk kedua butir soal adalah 35.

39. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :39/71
TUGAS
A. Translasi (Pertemuan ...................)
Kerjakan Uji Kompetensi 4.1 (halaman 149-150) nomor 1 samapai dengan 5 pada buku siswa.
B. Refleksi (Pertemuan ...................)
Kerjakan Uji Kompetensi 4.1(halaman 151) nomor 6 dan 7 pada buku siswa.
C. Rotasi (Pertemuan ...................)
Kerjakan Uji Kompetensi 4.2 (halaman 160) nomor 1 dan 2 pada buku siswa.
D. Translasi (Pertemuan ...................)
Kerjakan Uji Kompetensi 4.2 (halaman 161) nomor 3 dan 4 pada buku siswa.
E. Komposisi Transformasi (Pertemuan ...................)
Kerjakan Uji Kompetensi 4.3 (halaman 173) nomor 1 sampai dengan 5 pada buku siswa.

40. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :40/71
Mata Pelajaran/Materi : Matematika/Transformasi
Kelas/Semester : XI/Ganjil
Alokasi Waktu : 30 𝑚𝑒𝑛𝑖𝑡
Nama Kelompok : ......................................
Nama Anggota Kelompok :
1.…………………………………
2.…………………………………
3.…………………………………
4.…………………………………
5.…………………………………
1. Melatih sikap sosial berani bertanya, berpendapat, mau mendengar orang lain, bekerja sama dalam
diskusi di kelompok sehingga terbiasa berani bertanya, berpendapat, mau mendengar orang lain,
bekerja sama dalam aktivitas sehari-hari.
2. Menunjukkan rasa ingin tahu selama mengikuti proses pembelajaran.
3. Bertanggung jawab terhadap kelompoknya dalam menyelesaikan tugasnya.
4. Menyebutkan contoh translasi dalam kehidupan sehari-hari.
5. Menemukan sifat-sifat translasi berdasarkan pengamatan pada masalah kontekstual dan penga-
matan objek pada bidang koordinat.
6. Menemukan konsep translasi dengan kaitannya dengan konsep matriks.
7. Terampil menemukan matriks translasi dengan pengamatan terhadap titik-titik dan bayangannya
8. Terampil menggunakan konsep translasi dengan kaitannya dengan konsep matriks dalam
menemukan koordinat titik atau fungsi setelah ditransformasi.
TRANSLASI
(PERGESERAN)
LEMBAR KEGIATAN PESERTA DIDIK (4a)
TUJUAN PEMBELAJARAN

41. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :41/71
ALAT & BAHANRUMUSAN MASALAH
1. Bagaimanakah contoh translasi dalam 1. Kertas
kehidupan sehari-hari? 2. Alat Tulis
2. Bagaimanakah sifat-sifat translasi? 3. Buku Berpetak
3. Bagaimanakah kaitan antara konsep translasi 4. Penggaris
dengan konsep matriks?
1. Isilah nama dan anggota kelompoknya pada tempat yang telah disediakan.
2. Baca dan pahami pernyataan-pernyataan dari masalah yang disajikan dalam LKPD berikut, kemudian
pikirkan kemungkinan jawabannya.
3. Silahkan melakukan diskusi kelompok terhadap tugas telah disajikan tersebut dan catatlah jawaban
kalian pada tempat yang telah disediakan .
4. Jika terdapat masalah yang tidak dapat diselesaikan, tanyakan kepada guru.
5. Tugas dikerjakan selama maksimal 30 menit.
6. Setelah diskusi kelompok selesai, persiapkan seorang anggota kelompok untuk menjadi juru bicara.
7. Juru bicara yang terpilih akan mempresntasikan hasil diskusi dari kelompoknya, sementara anggota
kelompoknya mempersiapkan diri memberi jawaban atau tanggapan dari kelompok lain.
Abiyyu saat ini merencanakan
membangun suatu rumah di
desa kelahirannya. Diketahui
Abiyyu memiliki lahan di dua
tempat yakni di samping
lapangan sepak bola dan tepat di
seberang jalan dengan luas yang
sama. Abiyyu merancang
sebuah rumah di atas bidang
kartesius seperti gambar di
samping!
LANGKAH-LANGKAH KEGIATAN
Materi awal yang harus dikuasai:
1. Koordinat Kartesius
2. Operasi Pada Matriks
3. Persamaan Garis Lurus
PERMASALAHAN 1
JalanPerintisKemerdekaan

42. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :42/71
Kemudian, setelah rumah Abiyyu dipindahkan, apakah terdapat perubahan bentuk, ukuran atau posisi?
Jika ya, mengapa?
......................................................................................................................................................................
......................................................................................................................................................................
Jika tidak, mengapa?
......................................................................................................................................................................
......................................................................................................................................................................
Berdasarkan permasalahan 1 di atas, anda dapat menyimbulkan bahwa translasi memiliki
beberapa sifat-sifat, antara lain:
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
Phytagoras: “Jangan katakan hal-hal kecil dengan banyak kata-kata,
Tapi katakanlah sesuatu yang besar dengan sedikit kata”
Ternyata Abiyyu merasa letak rumah tersebut tidak strategis. Kemudian, Abiyyu
memindahkan rumahnya di dekat lapangan bola (Keterangan: Jarak dari suatu
bangunan di samping bangunan sama dengan jarak bangunan tersebut ke
seberangnya.
Maka, koordinat titik-titik rumah berpindah dari titik:
.................................................................................................................................................................
.................................................................................................................................................................
Ke titik:
.................................................................................................................................................................
.................................................................................................................................................................
Dalam matematika, ilustrasi di atas dinamakan dengan Translasi.
Jadi dapat disimpulkan, yang dimaksud Translasi adalah:
..............................................................................................
..............................................................................................
..............................................................................................
..............................................................................................
..........................

43. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :43/71
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
PERMASALAHAN 2
Buatlah ilustrasi lain mengenai translasi pada koordinat kartesius
dan gambarkan pada buku berpetak atau kertas berpetak.
Setelah memahami konsep translasi, ayo berlatih dengan
menyelesaikan soal berikut ini:
1. Tentukanlah titik akhir dari pergeseran berikut:
a. Titik 𝐴(2,−3) bila ditranslasikan dengan 𝑇 = (
3
4
)
b. Titik 𝐵(2, −3) bila ditranslasikan dengan 𝑇 = (
3
4
) dilanjutkan dengan 𝑇 = (
−1
−3
)
2. Tentukan persamaan kurva oleh translasi 𝑇 berikut:
a. Garis lurus 2𝑥 − 3𝑦 + 4 = 0 dengan 𝑇 = (
2
−1
)
b. Parabola 𝑦 = 𝑥2 + 𝑥 − 6 terhadap garis 𝑇 = (
1
−1
)
3. Buatalah suatu pergeseran dari suatu titik sebarang dengan 𝑇 sebarang!
SOLUSI

44. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :44/71
Mata Pelajaran/Materi : Matematika/Transformasi
Kelas/Semester : XI/Ganjil
Alokasi Waktu : 30 𝑚𝑒𝑛𝑖𝑡
Nama Kelompok : ......................................
Nama Anggota Kelompok :
1.…………………………………
2.…………………………………
3.…………………………………
4.…………………………………
5.…………………………………
6.…………………………………
1. Melatih sikap sosial berani bertanya, berpendapat, mau mendengar orang lain, bekerja sama dalam
diskusi di kelompok sehingga terbiasa berani bertanya, berpendapat, mau mendengar orang lain,
bekerja sama dalam aktivitas sehari-hari.
2. Menunjukkan rasa ingin tahu selama mengikuti proses pembelajaran.
3. Bertanggung jawab terhadap kelompoknya dalam menyelesaikan tugasnya.
4. Menyebutkan contoh refleksi dalam kehidupan sehari-hari.
5. Menemukan sifat-sifat refleksi berdasarkan pengamatan pada masalah kontekstual dan pengamatan
objek pada bidang koordinat.
6. Menemukan konsep refleksi terhadap titik 𝑂(0,0) dengan kaitannya dengan konsep matriks.
7. Menemukan konsep refleksi terhadap sumbu x dengan kaitannya dengan konsep matriks.
8. Menemukan konsep refleksi terhadap sumbu y dengan kaitannya dengan konsep matriks.
REFLEKSI
(PENCERMINAN)
TUJUAN PEMBELAJARAN
LEMBAR KEGIATAN PESERTA DIDIK (4b)

45. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :45/71
9. Menemukan konsep refleksi terhadap garis 𝑦 = 𝑥 dengan kaitannya dengan konsep matriks.
10. Menemukan konsep refleksi terhadap garis 𝑦 = −𝑥 dengan kaitannya dengan konsep matriks.
11. Membandingkan jenis transformasi (translasi dan refleksi) dengan menyebutkan perbedaannya.
12. Terampil menemukan matriks refleksi dengan pengamatan terhadap titik-titik dan bayangannya
13. Terampil menggunakan konsep refleksi dengan kaitannya dengan konsep matriks dalam
menemukan koordinat titik atau fungsi setelah ditransformasi.
14. Terampil membandingkan proses transformasi (translasi dan refleksi).
1. Bagaimanakah contoh refleksi dalam
kehi-dupan sehari-hari?
2. Bagaimanakah sifat-sifat refleksi?
3. Bagaimanakah cara menemukan konsep
refleksi terhadap titik 𝑂(0,0) dengan
kaitannya dengan konsep matriks?
4. Bagaimanakah cara menemukan konsep
refleksi terhadap sumbu x dengan
kaitannya dengan konsep matriks?
5. Bagaimanakah cara menemukan konsep refleksi
terhadap sumbu y dengan kaitannya dengan konsep
matriks?
6. Bagaimanakah cara menemukan konsep refleksi
terhadap garis 𝑦 = 𝑥 dengan kaitannya dengan
konsep matriks?
7. Bagaimanakah cara menemukan konsep refleksi
terhadap garis 𝑦 = −𝑥 dengan kaitannya dengan
konsep matriks?
8. Bagaimanakah perbedaan translasi dan refleksi?
1. Kertas 3. Buku Berpetak 5. Cermin (Jika Ada)
2. Alat Tulis 4. Penggaris
1. Isilah nama dan anggota kelompoknya pada tempat yang telah disediakan.
2. Baca dan pahami pernyataan-pernyataan dari masalah yang disajikan dalam LKPD berikut, kemudian
pikirkan kemungkinan jawabannya.
3. Silahkan melakukan diskusi kelompok terhadap tugas telah disajikan tersebut dan catatlah jawaban
kalian pada tempat yang telah disediakan .
4. Jika terdapat masalah yang tidak dapat diselesaikan, tanyakan kepada guru.
5. Tugas dikerjakan selama maksimal 30 menit.
6. Setelah diskusi kelompok selesai, persiapkan seorang anggota kelompok untuk menjadi juru bicara.
7. Juru bicara yang terpilih akan mempresntasikan hasil diskusi dari kelompoknya, sementara anggota
kelompoknya mempersiapkan diri memberi jawaban atau tanggapan dari kelompok lain.
Materi awal yang harus dikuasai:
1. Koordinat Kartesius
2. Operasi Pada Matriks
3. Persamaan Garis Lurus

46. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :46/71
Sebuah bangunan masjid terlihat cerminannya di atas permukaan air seperti pada gambar berikut!
Berdasarkan gambar di atas, dapatkah kalian menjelaskan sifat-sifat pencerminan:
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
......................................................................................................................................................................
Diketahui segitiga ABC dengan
titik 𝐴(2,1) 𝐵(7,3) dan 𝐶(4,5).
Gambarlah bayangan
segitiga 𝐴𝐵𝐶 jika dicerminkan
terhadap :
a. Titik 𝑂(0,0)
b. Garis 𝑦 = 𝑥
c. Sumbu 𝑥
d. Garis 𝑦 = −𝑥
e. Sumbu 𝑦
PERMASALAHAN 1
PERMASALAHAN 2

47. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :47/71
Dari beberapa gambar yang dibuat, maka dapat disimpulkan terdapat beberapa jenis pencer-
minan. Antara lain:
a. Jika titik 𝐴(𝑥, 𝑦) dicerminkan terhadap sumbu 𝑂(0,0) maka bayangan 𝐴´(.. ., .. ..)
b. Jika titik 𝐴(𝑥, 𝑦) dicerminkan terhadap sumbu 𝑥, maka bayangan 𝐴´(... ,. .. .)
c. Jika titik 𝐴(𝑥, 𝑦) dicerminkan terhadap sumbu 𝑦, maka bayangan 𝐴´(.. ., ... .)
d. Jika titik 𝐴(𝑥, 𝑦) dicerminkan terhadap garis 𝑦 = 𝑥 maka bayangan 𝐴´(.. ., ... .)
e. Jika titik 𝐴(𝑥, 𝑦) dicerminkan terhadap garis 𝑦 = −𝑥 maka bayangan 𝐴´(.. ., ... .)
PERMASALAHAN 3
Buatlah ilustrasi lain mengenai refleksi pada koordinat kartesius
dan gambarkan pada buku berpetak atau kertas berpetak.
Jadi dapat disimpulkan, yang dimaksud Refleksi adalah:
..............................................................................................
..............................................................................................
..............................................................................................
..............................................................................................
..........................
Setelah memahami konsep translasi,
ayo berlatih dengan menyelesaikan soal berikut ini:
1. Tentukanlah hasil pencerminan dari beberapa titik berikut:
a. Titik 𝐴(2,−3) bila dicerminkan dengan 𝑇 = (
3
4
)
b. Titik 𝐵(2, −3) bila dicerminkan terhadap sumbu 𝑦 dilanjut
terhadap garis 𝑥 = 2.
2. Tentukan persamaan kurva oleh pencerminan berikut:
a. Garis lurus 2𝑥 − 3𝑦 + 4 = 0 dicerminkan terhadap sumbu 𝑥.
b. Parabola 𝑦 = 𝑥2 + 𝑥 − 6 terhadap garis 𝑦 = 3
3. Buatlah suatu pencerminan dari suatu titik sebarang terhadap
sumbu koordinat kartesius 𝑥 atau 𝑦.

48. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :48/71
Mata Pelajaran/Materi : Matematika/Transformasi
Kelas/Semester : XI/Ganjil
Alokasi Waktu : 30 𝑚𝑒𝑛𝑖𝑡
Nama Kelompok : ......................................
Nama Anggota Kelompok :
1. …………………………………
2.…………………………………
3.…………………………………
4.…………………………………
5.…………………………………
6.…………………………………
1. Melatih sikap sosial berani bertanya, berpendapat, mau mendengar orang lain, bekerja sama dalam
diskusi di kelompok sehingga terbiasa berani bertanya, berpendapat, mau mendengar orang lain,
bekerja sama dalam aktivitas sehari-hari.
2. Menunjukkan rasa ingin tahu selama mengikuti proses pembelajaran.
3. Bertanggung jawab terhadap kelompoknya dalam menyelesaikan tugasnya.
4. Menyebutkan contoh rotasi dalam kehidupan sehari-hari.
5. Menemukan sifat-sifat rotasi berdasarkan pengamatan pada masalah kontekstual dan pengamatan
objek pada bidang koordinat.
6. Menemukan konsep rotasi pada suatu sudut dan pusat 𝑂(0,0) dengan kaitannya dengan konsep
matriks.
7. Menemukan konsep rotasi pada suatu sudut dan pusat 𝑃(𝑝, 𝑞) dengan kaitannya dengan konsep
matriks.
ROTASI
(PERPUTARAN)
LEMBAR KEGIATAN PESERTA DIDIK (4c)
TUJUAN PEMBELAJARAN

49. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :49/71
LANGKAH-LANGKAH KEGIATAN
RUMUSAN MASALAH
ALAT DAN BAHAN
8. Membandingkan jenis transformasi (translasi, refleksi & rotasi) dengan menyebutkan perbedaannya.
9. Terampil menemukan matriks rotasi dengan pengamatan terhadap titik-titik dan bayangannya.
10. Terampil menggunakan konsep rotasi dengan kaitannya dengan konsep matriks dalam menemukan
koordinat titik atau fungsi setelah ditransformasi.
11. Terampil membandingkan proses transformasi (translasi, refleksi dan rotasi).
1. Bagaimanakah contoh rotasi dalam kehidupan sehari-hari?
2. Bagaimanakah sifat-sifat rotasi?
3. Bagaimanakah konsep rotasi pada suatu sudut dan pusat 𝑂(0,0) dengan kaitannya dengan konsep
matriks?
4. Bagaimanakah konsep rotasi pada suatu sudut dan pusat 𝑃(𝑝, 𝑞) dengan kaitannya dengan konsep
matriks?
5. Bagaimakah perbedaan translasi, refleksi dan rotasi?
1. Kertas 3. Penggaris 5. Tabel Trigonometri
2. Alat Tulis 4. Buku Berpetak
1. Isilah nama dan anggota kelompoknya pada tempat yang telah disediakan.
2. Baca dan pahami pernyataan-pernyataan dari masalah yang disajikan dalam LKPD berikut, kemudian
pikirkan kemungkinan jawabannya.
3. Silahkan melakukan diskusi kelompok terhadap tugas telah disajikan tersebut dan catatlah jawaban
kalian pada tempat yang telah disediakan .
4. Jika terdapat masalah yang tidak dapat diselesaikan, tanyakan kepada guru.
5. Tugas dikerjakan selama maksimal 30 menit.
6. Setelah diskusi kelompok selesai, persiapkan seorang anggota kelompok untuk menjadi juru bicara.
7. Juru bicara yang terpilih akan mempresntasikan hasil diskusi dari kelompoknya, sementara anggota
kelompoknya mempersiapkan diri memberi jawaban atau tanggapan dari kelompok lain.
Materi awal yang harus dikuasai:
1. Koordinat Kartesius
2. Operasi Pada Matriks
3. Persamaan Garis Lurus
4. Trigonometri

50. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :50/71
Diketahui Segitiga ABC dengan titik 𝐴(2,1), 𝐵(7,3), 𝐶(4,5)! Sketsalah letak kedudukan segitiga ABC
diatas jika berotasi dengan pusat di titik 𝑂(0,0) dan pilihlah besar sudut rotasinya adalah sudut-sudut
istimewa yang pernah kalian pelajari (90°,−90°,180°,−180°, 270°,−270°)!
Rotasi sejauh ............ dengan Pusat rotasi ........................
Titik Objek Titik Bayangan Pola
𝐴(……. ,… …. ) 𝐴′(……. ,… …. ) (
. . . …
… …)(
…
…) = (
…
…)
𝐵(…… ., …… .) 𝐵′(……. ,… …. ) (
. . . …
… …)(
…
…) = (
…
…)
𝐶(… …. ,… …. ) 𝐶′(… …. ,…… .) (
. . . …
… …)(
…
…) = (
…
…)
Dengan demikian, rotasi .......... dengan pusat ...........
Diwakili dengan matriks 𝑅(……… ,……...) = (… …… , …… …)
Sketsa gambarnya adalah:
Diketahui Segitiga 𝐴𝐵𝐶 dengan titik 𝐴(2,1) 𝐵(7,1) dan 𝐶(7,5)! Jika segitiga tersebut berotasi dengan
pusat P(3,4) dan pilihlah salah satu besar sudut rotasinya yang pernah kalian pelajari
(90°,−90°,180°, −180°,270°,−270°)!
PERMASALAHAN 1
PERMASALAHAN 2

51. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :51/71
SOAL LATIHAN
Rotasi sejauh ............ dengan Pusat rotasi ........................
Titik Objek
Translasi
𝑇(−3, −4)
Rotasi ...........
Pusat 𝑂(0,0) Translasi 𝑃(3,4) = Titik Bayangan
𝐴(2,1) 𝐴1(−1 ,−3) 𝐴2(……. ,…… .)
(……. ,… ….) + (… …. ,… ….)
= (…… ., …… .)
𝐵(…… ., …… .) 𝐵1(……. ,… …. ) 𝐵2(…… ., …… .)
(……. ,… ….) + (… …. ,… ….)
= (…… ., …… .)
𝐶(… …. ,… …. ) 𝐶1(…… ., …… .) 𝐶2(……. ,… …. )
(……. ,… ….) + (… …. ,… ….)
= (…… ., …… .)
Sketsakan letak kedudukan segitiga ABC diatas pada buku berpetak dan tempelkan pada kertas HVS!
Definisi dari Rotasi:
___________________________________________
___________________________________________
___________________________________________
___________________________________________
Sifat dari Rotasi:
___________________________________________
___________________________________________
___________________________________________
___________________________________________
1. Tentukanlah titik akhir dari perputaran berikut:
a. Titik 𝐴(2,−3) bila dirotasikan sebesar 90° dengan pusat
𝑂(0,0).
b. Titik 𝐵(4,5) bila dirotasi sebesar −90° dengan pusat 𝑂(0,0)
dilanjutkan rotasi sebesar 180° dengan pusat (1,1).
2. Tentukan persamaan kurva oleh rotasi 𝑅 berikut:
a. Garis lurus 2𝑥– 3𝑦 + 4 = 0 dirotasi sebesar 90° dengan
pusat 𝑂(0,0).
b. Parabola 𝑦 = 𝑥2 + 𝑥– 6 dirotasi sebesar −180° dengan
pusat 𝑂(0,0).
Dari ilustrasi di atas
dapat disimpulkan
bahwa:
Seteleh memahai konsep
rotasi dapatkah kalian
menentukan soal-soal
dibawah ini:

52. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :52/71
Mata Pelajaran/Materi : Matematika/Transformasi
Kelas/Semester : XI/Ganjil
Alokasi Waktu : 30 𝑚𝑒𝑛𝑖𝑡
Nama Kelompok : ......................................
Nama Anggota Kelompok :
1. …………………………………
2.…………………………………
3.…………………………………
4.…………………………………
5.…………………………………
6.…………………………………
1. Melatih sikap sosial berani bertanya, berpendapat, mau mendengar orang lain, bekerja sama dalam
diskusi di kelompok sehingga terbiasa berani bertanya, berpendapat, mau mendengar orang lain,
bekerja sama dalam aktivitas sehari-hari.
2. Menunjukkan rasa ingin tahu selama mengikuti proses pembelajaran.
3. Bertanggung jawab terhadap kelompoknya dalam menyelesaikan tugasnya.
4. Menyebutkan contoh dilatasi dalam kehidupan sehari-hari.
5. Menemukan sifat-sifat dilatasi berdasarkan pengamatan pada masalah kontekstual dan pengamatan
objek pada bidang koordinat.
6. Menemukan konsep dilatasi pada faktor skala 𝑘 dan pusat 𝑂(0,0) dengan kaitannya dengan konsep
matriks.
7. Menemukan konsep dilatasi pada faktor skala 𝑘 dan pusat 𝑃(𝑝, 𝑞) dengan kaitannya dengan konsep
matriks.
8. Membandingkan keempat jenis transformasi dengan menyebutkan perbedaannya.
LEMBAR KEGIATAN PESERTA DIDIK (4d)
DILATASI
(PERKALIAN)
TUJUAN PEMBELAJARAN

53. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :53/71
9. Terampil menemukan matriks dilatasi dengan pengamatan terhadap titik-titik dan bayangannya.
10. Terampil menggunakan konsep dilatasi dengan kaitannya dengan konsep matriks dalam menemu-
kan koordinat titik atau fungsi setelah ditransformasi.
11. Terampil membandingkan keempat proses transformasi (translasi, refleksi, rotasi dan dilatasi).
1. Bagaimanakah contoh dilatasi dalam kehidupan sehari-hari?
2. Bagaimanakah sifat-sifat dilatasi?
3. bagaimanakah konsep dilatasi pada faktor skala 𝑘 dan pusat 𝑂(0,0) dengan kaitannya dengan
konsep matriks.
4. bagaimanakah konsep dilatasi pada faktor skala 𝑘 dan pusat 𝑃(𝑝, 𝑞) dengan kaitannya dengan
konsep matriks.
5. Bagaimakah perbedaan translasi, refleksi, rotasi dan dilatasi?
1. Kertas 3. Penggaris 5. Miniatur (Bila tersedia)
2. Alat Tulis 4. Buku Berpetak 6. Balon
1. Isilah nama dan anggota kelompoknya pada tempat yang telah disediakan.
2. Baca dan pahami pernyataan-pernyataan dari masalah yang disajikan dalam LKPD berikut, kemudian
pikirkan kemungkinan jawabannya.
3. Silahkan melakukan diskusi kelompok terhadap tugas telah disajikan tersebut dan catatlah jawaban
kalian pada tempat yang telah disediakan .
4. Jika terdapat masalah yang tidak dapat diselesaikan, tanyakan kepada guru.
5. Tugas dikerjakan selama maksimal 30 menit.
6. Setelah diskusi kelompok selesai, persiapkan seorang anggota kelompok untuk menjadi juru bicara.
7. Juru bicara yang terpilih akan mempresntasikan hasil diskusi dari kelompoknya, sementara anggota
kelompoknya mempersiapkan diri memberi jawaban atau tanggapan dari kelompok lain.
RUMUSAN MASALAH
ALAT DAN BAHAN
LANGKAH-LANGKAH KEGIATAN
Materi awal yang harus dikuasai:
1. Koordinat Kartesius
2. Operasi Pada Matriks
3. Persamaan Garis Lurus

54. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :54/71
Diketahui beberapa segitiga dengan titik-titiknya sebagai berikut:
Nama Segitiga Titik Objek Titik Objek Titik Objek
𝐴𝐵𝐶 𝐴(2,2) 𝐵(6,2) 𝐶(6,5)
𝐷𝐸𝐹 𝐷(−2,2) 𝐸(−2,5) 𝐹(−6,2)
𝐺𝐻𝐼 𝐺(2, −2) 𝐻(2,−5) 𝐼(6,−5)
𝐽𝐾𝐿 𝐽(−6,2) 𝐾(−6, −5) 𝐿(−2, −5)
𝑀𝑁𝑂 𝑀(1,0) 𝑁(1,4) (0,−3)
Sketsalah salah satu segitiga di atas. Kemudian, jarak titik sudutna terhadap 𝑂(0,0) diperbesar menjadi
2 kali lipat dan diperkecil
1
2
kali lipat.
Titik Objek
Titik Bayangan
Faktor Skala 2 Faktor Skala
𝟏
𝟐
..... ( , ) ..... ( , ) ..... ( , )
..... ( , ) ..... ( , ) ..... ( , )
..... ( , ) ..... ( , ) ..... ( , )
Sketasa Segitiganya adalah:
PERMASALAHAN 1

55. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :55/71
Definisi dari Dilatasi:
........................................................................................
........................................................................................
........................................................................................
........................................................................................
Sifat dari Dilatasi:
........................................................................................
........................................................................................
........................................................................................
........................................................................................
Diketahui beberapa segitiga dengan keterangan di bawah ini:
Nama Segitiga Titik Objek Titik Objek Titik Objek Titik Pusat Faktor Skala
𝐴𝐵𝐶 𝐴(2,2) 𝐵(6,2) 𝐶(6,5) 𝑃(2,2)
𝑘 = 3
𝐷𝐸𝐹 𝐷(−2,2) 𝐸(−2,5) 𝐹(−6,2) 𝑃(1,1)
𝐺𝐻𝐼 𝐺(2,−2) 𝐻(2, −5) 𝐼(6,−5) 𝑃(−2,−2)
𝐽𝐾𝐿 𝐽(−6,2) 𝐾(−6,−5) 𝐿(−2, −5) 𝑃(2, −2)
𝑀𝑁𝑂 𝑀(1,0) 𝑁(1,4) (0,−3) 𝑃(2, −1)
Pilihlah empat dari segitiga di atas dan tentukan titik baangannya dengan faktor skala 𝑘 = 3
Titik Objek
Segitiga ...........
Faktor Skala 3
Titik Bayangan
..... ( , ) ..... ( , )
..... ( , ) ..... ( , )
..... ( , ) ..... ( , )
Titik Objek
Segitiga ...........
Faktor Skala 3
Titik Bayangan
..... ( , ) ..... ( , )
..... ( , ) ..... ( , )
..... ( , ) ..... ( , )
Titik Objek
Segitiga ...........
Faktor Skala 3
Titik Bayangan
..... ( , ) ..... ( , )
..... ( , ) ..... ( , )
..... ( , ) ..... ( , )
Titik Objek
Segitiga ...........
Faktor Skala 3
Titik Bayangan
..... ( , ) ..... ( , )
..... ( , ) ..... ( , )
..... ( , ) ..... ( , )
Sketsakanlah keempat segitiga tersebut pada kertas berpetak dan tempelkan pada kertas HVS
(dikerjakan oleh masing-masing anggota kelompok!).
Kegiatan yang telah dilakukan sebelumnya pada Permasalahan 1 dinamakan DILATASI dengan
notasi D. Skala atau faktor perbesaran dinotasikan dengan k dan k tidak harus bilangan bulat.
Dari ilustrasi di
atas, dapat
disimpulkan
bahwa...
PERMASALAHAN 2

56. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :56/71
SOAL LATIHAN
ALTERNATIF
PENYELESAIAN
1. Tentukanlah dilatasi dari beberapa berikut:
a. Titik A(2,-3) bila didilatasi dengan skala 2 dan pusat O(0,0).
b. Titik B(-3,4) bila didilatasi dengan skala 3 dan pusat P(1,1) dilanjutkan dilatasi dengan skala
dengan pusat P(0,0).
2. Tentukan persamaan kurva oleh dilatasi D berikut:
a. Garis lurus 2x – 3x + 4 = 0 didilatasi faktor skala 2 dengan pusat O(0,0).
b. Parabola y = x2 + x – 6 didilatasi dengan faktor skala 2 dengan pusat O(0,0).
3. Cermati soal dibawah ini:
Buatlah suatu dilatasi dari suatu titik sebarang dengan faktor skala k dengan pusat O(0,0)!
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
Seteleh memahai konsep rotasi dapatkah kalian
menentukan soal-soal dibawah ini:

57. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :57/71
Mata Pelajaran/Materi : Matematika/Transformasi
Kelas/Semester : XI/Ganjil
Alokasi Waktu : 30 𝑚𝑒𝑛𝑖𝑡
Nama Kelompok : ......................................
Nama Anggota Kelompok :
1.…………………………………
2.…………………………………
3.…………………………………
4.…………………………………
5.…………………………………
6.…………………………………
1. Melatih sikap sosial berani bertanya, berpendapat, mau mendengar orang lain, bekerja sama dalam
diskusi di kelompok sehingga terbiasa berani bertanya, berpendapat, mau mendengar orang lain,
bekerja sama dalam aktivitas sehari-hari.
2. Menunjukkan rasa ingin tahu selama mengikuti proses pembelajaran.
3. Bertanggung jawab terhadap kelompoknya dalam menyelesaikan tugasnya.
4. Menemukan konsep komposisi transformasi (translasi, refleksi, rotasi, dan dilatasi).
Bagaimanakah konsep komposisi transformasi (translasi, refleksi, rotasi, dan dilatasi)?
1. Kertas 2. Alat Tulis 3. Buku Berpetak 4. Penggaris
LEMBAR KEGIATAN PESERTA DIDIK (4e)
Komposisi
Transformasi
TUJUAN PEMBELAJARAN
RUMUSAN MASALAH
ALAT DAN BAHAN

58. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :58/71
1. Isilah nama dan anggota kelompoknya pada tempat yang telah disediakan.
2. Baca dan pahami pernyataan-pernyataan dari masalah yang disajikan dalam LKPD berikut, kemudian
pikirkan kemungkinan jawabannya.
3. Silahkan melakukan diskusi kelompok terhadap tugas telah disajikan tersebut dan catatlah jawaban
kalian pada tempat yang telah disediakan .
4. Jika terdapat masalah yang tidak dapat diselesaikan, tanyakan kepada guru.
5. Tugas dikerjakan selama maksimal 30 menit.
6. Setelah diskusi kelompok selesai, persiapkan seorang anggota kelompok untuk menjadi juru bicara.
7. Juru bicara yang terpilih akan mempresntasikan hasil diskusi dari kelompoknya, sementara anggota
kelompoknya mempersiapkan diri memberi jawaban atau tanggapan dari kelompok lain.
1. Tentukan koordinat titik 𝐴(2,3) setelah ditranslasikan dengan 𝑇(−5,−5) kemudian dilanjutkan
dengan translasi 𝑈(−5, −5)!
2. Tentukan persamaan parabola 3𝑦 = 6 − 9𝑥 − 3𝑥2 setelah ditranslasi dengan 𝑇 ○ 𝑈 ○ 𝑇, dimana
𝑇(1,3) dan 𝑈(−1, −3)!
--------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
LANGKAH-LANGKAH KEGIATAN
Materi awal yang harus dikuasai:
1. Koordinat Kartesius 4. Translasi 7. Dilatasi
2. Operasi Pada Matriks 5. Refleksi
3. Persamaan Garis Lurus 6. Rotasi
PERMASALAHAN 1
KOMPOSISI TRANSLASI
ALTERNATIF PENYELESAIAN

59. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :59/71
Jika 𝐶 adalah pencerminan teradap titik 𝑂(0,0), 𝐸 adalah pencerminan terhadap sumbu 𝑥, 𝐹 adalah
pencerminan terhadap sumbu 𝑦, 𝐺 adalah pencerminan terhadap garis 𝑦 = 𝑥 dan 𝐻 adalah
pencerminan terhadap garis 𝑦 = −𝑥 maka tentukan koordinat bayangan oleh komposisi pencerminan
berikut:
1. Titik 𝑌(−4,4) dicerminkan dengan 𝐻 ○ 𝐹 ○ 𝐺 ○ 𝐸 ○ 𝐶 ○ 𝐺!
2. Parabola −𝑦 + 2𝑥2 − 5𝑥 + 6 = 0 dicerminkan dengan 𝐻 ○ 𝐺 ○ 𝐶!
--------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
Jika 𝑅 𝑘 adalah rotasi ke-k sejauh 90° berlawanan arah jarum jam dengan masing-masing pada pusat
𝑂(0,0) maka tentukan rotasi titik 𝐴(−2,−4) oleh 𝑅1 ○ 𝑅2 ○ … ○ 13
--------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
PERMASALAHAN 2
KOMPOSISI REFLEKSI
ALTERNATIF PENYELESAIAN
PERMASALAHAN 3
KOMPOSISI ROTASI
ALTERNATIF PENYELESAIAN

60. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :60/71
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
Jika 𝐷 𝑘 adalah dilatasi ke-k dengan faktor skala ℎ pada pusat 𝑃(0, −2) maka tentukan dilatasi titik
𝐴(−3,6) oleh 𝐷1 ○ 𝐷2 ○ … .○ 𝐷9!
--------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
PERMASALAHAN 4
KOMPOSISI DILATASI
ALTERNATIF PENYELESAIAN

61. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :61/71
KISI-KISI DAN KARTU SOAL PENILAIAN HARIAN (KD 3.5)
MADRASAH ALIYAH AL-IKHLAS UJUNG-BONE
TAHUN PELAJARAN 2018/2019
Mata Pelajaran : Matematika Wajib Nama Penyusun : Muh. Alfiansyah, S.Pd., M.Pd.
Kelas/Semester : XI/Ganjil
NO. KOMPETENSI DASAR MATERI INDIKATOR SOAL
NOMOR
SOAL
1. 3.6 Menganalisis dan
membandingkan
transformasi dan
komposisi
transformasi dengan
menggunakan
matriks.
Translasi  Menemukan konsep translasi
dengan kaitannya dengan
konsep matriks.
Tentukan bayangan lingkaran ( 𝑥 − 3)2 + ( 𝑦 + 1)2 = 4 jika
ditranslasikan 






2
5
T !
1
Refleksi  Menemukan konsep refleksi
terhadap titik 𝑂(0, 0) dengan
kaitannya dengan konsep
matriks.
 Menemukan konsep refleksi
terhadap sumbu x dengan
kaitannya dengan konsep
matriks.
 Menemukan konsep refleksi
terhadap sumbu y dengan
kaitannya dengan konsep
matriks.
 Menemukan konsep refleksi
Tentukan bayangan jajargenjang 𝐴𝐵𝐶𝐷 dengan titik sudut
𝐴(−2,4), 𝐵(0, −5), 𝐶(3,2) dan 𝐷(1,11) jika:
a. Dicerminkan terhadap titik 𝑂(0,0).
b. Dicerminkan terhadap sumbu 𝑥 kemudian dilanjutkan
dengan pencerminan terhadap sumbu 𝑦.
c. Dicerminkan terhadap garis 𝑦 = 𝑥 kemudian dilanjutkan
dengan pencerminan terhadap garis 𝑦 = −𝑥
2

62. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :62/71
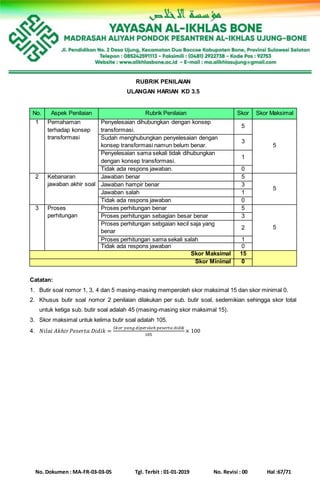
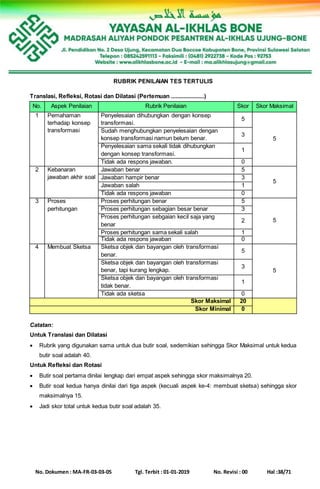
NO. KOMPETENSI DASAR MATERI INDIKATOR SOAL
NOMOR
SOAL
terhadap garis 𝑦 = 𝑥 dengan
kaitannya dengan konsep
matriks.
 Menemukan konsep refleksi
terhadap garis 𝑦 = −𝑥 dengan
kaitannya dengan konsep
matriks.
Rotasi  Menemukan konsep rotasi
pada suatu sudut dan pusat
𝑂(0,0) dengan kaitannya
dengan konsep matriks.
 Menemukan konsep rotasi
pada suatu sudut dan pusat
𝑃(𝑝, 𝑞) dengan kaitannya
dengan konsep matriks.
Tentukan bayangan titik 𝐴(−1,−2) yang dirotasi berturut-
turut sebesar 180° dan 90° berlawanan dengan arah
perputaran jarum jam dengan pusat yang sama, yaitu titik
𝑂(0,0)!
3
Dilatasi  Menemukan konsep dilatasi
pada faktor skala 𝑘 dan pusat
𝑂(0,0) dengan kaitannya
dengan konsep matriks.
 Menemukan konsep dilatasi
pada faktor skala 𝑘 dan pusat
𝑃(𝑝, 𝑞) dengan kaitannya
dengan konsep matriks.
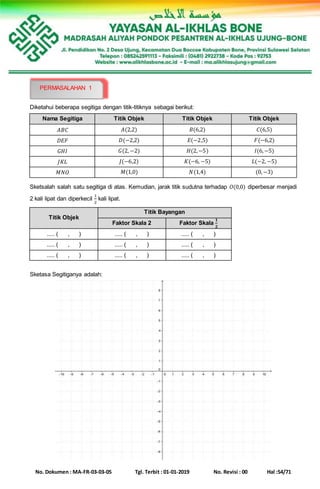
ABCD adalah sebuah persegi dengan koordinat titik-titik
sudut A(1,1), B(2,1), C(2,2) dan D(1,2). Tentukan peta atau
bayangan dari titik-titik sudut persegi itu oleh dilatasi [O,2]!
4

63. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :63/71
NO. KOMPETENSI DASAR MATERI INDIKATOR SOAL
NOMOR
SOAL
Komposisi
Transformasi
 Membandingkan keempat
jenis transformasi dengan
menyebutkan perbedaannya.
 Menemukan konsep
komposisi transformasi
(translasi, refleksi, rotasi, dan
dilatasi).
𝑇 adalah transformasi pencerminan terhadap garis 𝑦 = −𝑥.
𝑈 adalah transformasi perputaran setengah putaran
terhadap titik asal. Tentukan bayangan titik 𝑃(3,−5) yang
ditransformasikan terhadap 𝑇 dan dilanjutkan terhadap 𝑈!
5
Ujung, ....................................................
Guru Mata Pelajaran,
MUH. ALFIANSYAH, S.Pd., M.Pd.

64. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :64/71
UJIAN HARIAN
KD 3.3 DAN KD 3.4
Satuan Pendidikan : MA Pondok Pesantren Al-Ikhlas Bone
Mata Pelajaran : Matematika Wajib
Kelas /Semester : XI/1
Tahun Pelajaran : .....................................
Alokasi Waktu : 𝟐 × 𝟒𝟎 Menit (1 Pertemuan)
Petunjuk:
1. Tuliskan Nama Lengkap, NIS dan Kelas pada lembar jawaban.
2. Soal dapat dikerjakan secara acak (dahulukan soal yang dianggap mudah).
3. Tidak diperkenankan menggunakan alat bantu (kalkulator atau yang lainnya).
4. Tidak diperkenankan membuka buku catatan, bekerja sama, meminjam alat tulis dan menggu-
nakan pengalas (kecuali papan pengalas khusus ujian).
5. Soal yang kurang jelas ditanyakan langsung ke pengawas.
6. Lembar jawaban tidak akan diperiksa bagi peserta didik yang terbukti melakukan kecurangan saat
ujian
Soal:
1. Tentukan bayangan lingkaran ( 𝑥 − 3)2 + ( 𝑦 + 1)2 = 4 jika ditranslasikan 






2
5
T !
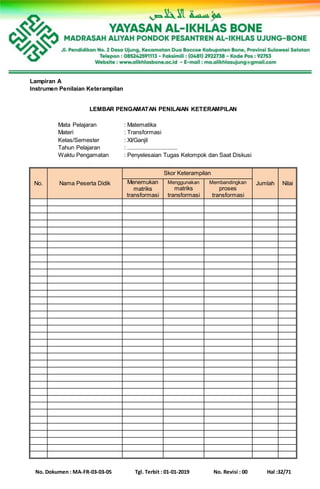
2. Tentukan bayangan jajargenjang 𝐴𝐵𝐶𝐷 dengan titik sudut 𝐴(−2,4), 𝐵(0, −5), 𝐶(3,2) dan 𝐷(1,11) jika:
a. Dicerminkan terhadap titik 𝑂(0,0).
b. Dicerminkan terhadap sumbu 𝑥 kemudian dilanjutkan dengan pencerminan terhadap sumbu 𝑦.
c. Dicerminkan terhadap garis 𝑦 = 𝑥 kemudian dilanjutkan dengan pencerminan terhadap garis 𝑦 =
−𝑥
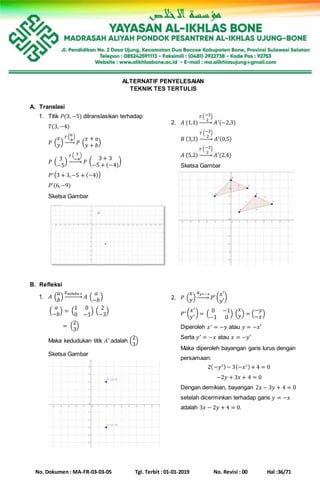
3. Tentukan bayangan titik 𝐴(−1,−2) yang dirotasi berturut-turut sebesar 180° dan 90° berlawanan
dengan arah perputaran jarum jam dengan pusat yang sama, yaitu titik 𝑂(0,0)!
4. ABCD adalah sebuah persegi dengan koordinat titik-titik sudut A(1,1), B(2,1), C(2,2) dan D(1,2).
Tentukan peta atau bayangan dari titik-titik sudut persegi itu oleh dilatasi [O,2]!
5. 𝑇 adalah transformasi pencerminan terhadap garis 𝑦 = −𝑥. 𝑈 adalah transformasi perputaran
setengah putaran terhadap titik asal. Tentukan bayangan titik 𝑃(3,−5) yang ditransformasikan
terhadap 𝑇 dan dilanjutkan terhadap 𝑈!
*Selamat Bekerja & Utamakan Kejujuran*

65. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :65/71
ALTERNATIF PENYELESAIAN
UJIAN HARIAN KD 3.5
1. Ambil sembarang titik P(a,b) pada lingkaran ( 𝑥 − 3)2 + ( 𝑦 + 1)2 = 4
sehingga diperoleh ( 𝑎 − 3)2 + ( 𝑏 + 1)2 = 4
Translasikan titik P dengan 






2
5
T sehingga diperoleh    2,5'', 2
5
 





 
baPbaP
Jadi titik 𝑃′(𝑎 − 5, 𝑏 + 2)
Perhatikan bahwa: 𝑎′ = 𝑎 − 5. Dari persamaan (*), didapat 𝑎 = 𝑎′ + 5.
𝑏′ = 𝑏 + 2. Dari persamaan (*), didapat 𝑏 = 𝑏′ − 2.
Dengan mensubstitusi nilai a dan b ini ke persamaan (*), akan
Diperoleh ( 𝑎′ + 5 − 3)2 + ( 𝑏′ − 2 + 1)2 = 4
( 𝑎′ + 2)2 + ( 𝑏′ − 1)2 = 4
Jadi bayangan dari ( 𝑎′ + 5 − 3)2 + ( 𝑏′ − 2 + 1)2 = 4 jika ditranslasikan dengan 






2
5
T adalah
( 𝑎′ + 2)2 + ( 𝑏′ − 1)2 = 4.
2. a. Dicerminkan terhadap titik 𝑂(0,0).
(
𝑥1
′
𝑥2
′
𝑥3
′
𝑥4
′
𝑦1
′
𝑦2
′ 𝑦3
′
𝑦4
′) = (
−1 0
0 −1
) (
−2 0 3 1
4 −5 −2 11
)
(
𝑥1
′
𝑥2
′
𝑥3
′
𝑥4
′
𝑦1
′
𝑦2
′ 𝑦3
′
𝑦4
′) = (
−1 0
0 −1
) (
−2 0 3 1
4 −5 −2 11
)
b. Dicerminkan terhadap sumbu 𝑥 kemudian dilanjutkan dengan pencerminan terhadap sumbu 𝑦.
(
𝑥1
′′
𝑥2
′′
𝑥3
′′
𝑥4
′′
𝑦1
′′
𝑦2
′′ 𝑦3
′′
𝑦4
′′) = (
−1 0
0 1
) (
1 0
0 −1
)(
−2 0 3 1
4 −5 −2 11
)
(
𝑥1
′′
𝑥2
′′
𝑥3
′′
𝑥4
′′
𝑦1
′′
𝑦2
′′ 𝑦3
′′
𝑦4
′′) = (
−1 0
0 −1
) (
−2 0 3 1
4 −5 −2 11
)
(
𝑥1
′′
𝑥2
′′
𝑥3
′′
𝑥4
′′
𝑦1
′′
𝑦2
′′ 𝑦3
′′
𝑦4
′′) = (
2 0 −3 −1
−4 5 2 −11
)
c. Dicerminkan terhadap garis 𝑦 = 𝑥 kemudian dilanjutkan dengan pencerminan terhadap garis
𝑦 = −𝑥
(
𝑥1
′′
𝑥2
′′
𝑥3
′′
𝑥4
′′
𝑦1
′′
𝑦2
′′ 𝑦3
′′
𝑦4
′′) = (
0 −1
−1 0
) (
0 1
1 0
)(
−2 0 3 1
4 −5 −2 11
)
(
𝑥1
′′
𝑥2
′′
𝑥3
′′
𝑥4
′′
𝑦1
′′
𝑦2
′′ 𝑦3
′′
𝑦4
′′) = (
−1 0
0 −1
) (
−2 0 3 1
4 −5 −2 11
)
(
𝑥1
′′
𝑥2
′′
𝑥3
′′
𝑥4
′′
𝑦1
′′
𝑦2
′′ 𝑦3
′′
𝑦4
′′) = (
2 0 −3 −1
−4 5 2 −11
)
3 Merotasi titik 𝐴(−1,−2) yang dirotasi berturut—turut sebesar 180° dan 90° berlawanan dengan
arah perputaran jarum jam dengan pusat yang sama, yaitu titik 𝑂(0,0) sama artinya merotasi titik
𝐴 sebesar 270° dengan pusat 𝑂(0,0):
Bayangan titik 𝐴 sebagai berikut:

66. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :66/71
𝐴′′ = ( 𝑎′′
𝑏′′
) = (
cos270 ° −sin 270°
sin 270° cos270°
) (
−1
−2
)
𝐴′′ = ( 𝑎′′
𝑏′′
) = (
0 1
−1 0
)(
−1
−2
)
𝐴′′ = ( 𝑎′′
𝑏′′
) = (
−2
1
)
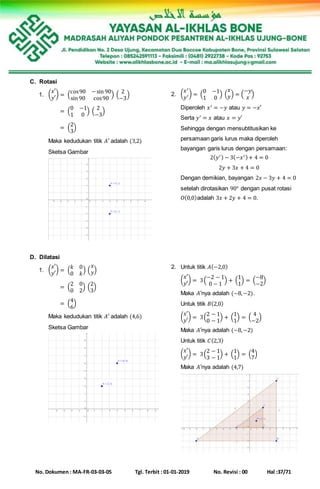
4. Peta atau bayangan titik-titik sudut persegi oleh dilatasi [𝑂,2]
Matriks yang bersesuaian dengan dilatasi [0,2] adalah (
2 0
0 2
)
Peta atau bayangan dari titik sudut persegi 𝐴(1,1), 𝐵(2,1), 𝐶(2,2) dan 𝐷(1,2) adalah
(
2 0
0 2
) (
1 2 2
1 1 2
1
2
) = (
2 4 4
2 2 4
2
4
)
Jadi peta dari titik-titik sudut 𝐴𝐵𝐶𝐷 adalah 𝐴’(2,2), 𝐵’(4,2), 𝐶’(4,4) dan 𝐷’(2,4).
5. 𝑀1 = (
0 −1
−1 0
) 𝑀2 = (
−1 0
0 −1
)
Transformasi 𝑈 ○ 𝑇:
𝑃(3,−5)
𝑈○𝑇
→ 𝑃′′
𝑃′′ = (
−1 0
0 −1
)(
0 −1
−1 0
) (
3
−5
)
𝑃′′ = (
0 1
1 0
) (
3
−5
)
𝑃′′ = (
−5
3
)
Jadi, bayangan akhir titik 𝑃(3, −5) terhadap transformasi 𝑇 dan 𝑈 adalah (−5,3).

67. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :67/71
RUBRIK PENILAIAN
ULANGAN HARIAN KD 3.5
No. Aspek Penilaian Rubrik Penilaian Skor Skor Maksimal
1 Pemahaman
terhadap konsep
transformasi
Penyelesaian dihubungkan dengan konsep
transformasi.
5
5
Sudah menghubungkan penyelesaian dengan
konsep transformasi namun belum benar.
3
Penyelesaian sama sekali tidak dihubungkan
dengan konsep transformasi.
1
Tidak ada respons jawaban. 0
2 Kebanaran
jawaban akhir soal
Jawaban benar 5
5
Jawaban hampir benar 3
Jawaban salah 1
Tidak ada respons jawaban 0
3 Proses
perhitungan
Proses perhitungan benar 5
5
Proses perhitungan sebagian besar benar 3
Proses perhitungan sebgaian kecil saja yang
benar
2
Proses perhitungan sama sekali salah 1
Tidak ada respons jawaban 0
Skor Maksimal 15
Skor Minimal 0
Catatan:
1. Butir soal nomor 1, 3, 4 dan 5 masing-masing memperoleh skor maksimal 15 dan skor minimal 0.
2. Khusus butir soal nomor 2 penilaian dilakukan per sub. butir soal, sedemikian sehingga skor total
untuk ketiga sub. butir soal adalah 45 (masing-masing skor maksimal 15).
3. Skor maksimal untuk kelima butir soal adalah 105.
4. 𝑁𝑖𝑙𝑎𝑖 𝐴𝑘ℎ𝑖𝑟 𝑃𝑒𝑠𝑒𝑟𝑡𝑎 𝐷𝑖𝑑𝑖𝑘 =
𝑆𝑘𝑜𝑟 𝑦𝑎𝑛𝑔 𝑑𝑖𝑝𝑒𝑟𝑜𝑙𝑒ℎ 𝑝𝑒𝑠𝑒𝑟𝑡𝑎 𝑑𝑖𝑑𝑖 𝑘
105
× 100

68. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :68/71
ANALISIS UJIAN HARIAN KD 3.5
TAHUN PELAJARAN 2019/2020
Satuan Pendidikan : MA Pondok Pesantren Al-Ikhlas Bone Ujian : Harian
Kelas /Semester : XI ..../2 KKM : .......
Mata Pelajaran : Matematika Wajib JUMLAH SOAL : 5
Tahun Pelajaran : 2019/2020
No. Nama Peserta Didik
Nomor Soal
Skor
Pero-
lehan
Perse-
ntase
Keter-
capaian
(%)
1 2a 2b 3 4 5
Konsep
Trans-
formasi
Kebenaran
Jawaban
Akhir
Proses
Perhitungan
Konsep
Trans-
formasi
Kebenaran
Jawaban
Akhir
Proses
Perhitungan
Konsep
Trans-
formasi
Kebenaran
Jawaban
Akhir
Proses
Perhitungan
Konsep
Trans-
formasi
Kebenaran
Jawaban
Akhir
Proses
Perhitungan
Konsep
Trans-
formasi
Kebenaran
Jawaban
Akhir
Proses
Perhitungan
Konsep
Trans-
formasi
Kebenaran
Jawaban
Akhir
Proses
Perhitungan

69. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :69/71
No. Nama Peserta Didik
Nomor Soal
Skor
Pero-
lehan
Perse-
ntase
Keter-
capaian
(%)
1 2a 2b 3 4 5
Konsep
Trans-
formasi
Kebenaran
Jawaban
Akhir
Proses
Perhitungan
Konsep
Trans-
formasi
Kebenaran
Jawaban
Akhir
Proses
Perhitungan
Konsep
Trans-
formasi
Kebenaran
Jawaban
Akhir
Proses
Perhitungan
Konsep
Trans-
formasi
Kebenaran
Jawaban
Akhir
Proses
Perhitungan
Konsep
Trans-
formasi
Kebenaran
Jawaban
Akhir
Proses
Perhitungan
Konsep
Trans-
formasi
Kebenaran
Jawaban
Akhir
Proses
Perhitungan
Jumlah Skor
Jumlah Skor Maksimum
Persentase Skor Ketercapaian

70. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :70/71
PEMBELAJARAN REMEDIAL & PENGAYAAN
KD 3.5
Nama Madrasah : MA AL-IKHLAS UJUNG
Mata Pelajaran : Matematika
Alokasi Waktu : 2 × 45 menit
Kelas/Semester : XI/Ganjil
Tahun Pelajaran : 2019/2020
Ujian Harian Ke- : 4
Bentuk Soal : Uraian
Materi Ujian Harian : Transformasi
Kompetensi Inti : Memahami, menerapkan, & menganalisis pengetahuan faktual, konseptual, pro-
sedural, dan metakognitif berdasarkan rasa ingin tahunya tentang ilmu pengeta-
huan, teknologi, seni, budaya, dan humaniora dengan wawasan kemanusiaan,
kebangsaan, kenegaraan, dan peradaban terkait penyebab fenomena dan
kejadian, serta menerapkan pengetahuan prosedural pada bidang kajian yang
spesifik sesuai dengan bakat dan minatnya untuk memecahkan masalah.
Kompetensi Dasar : 3.5 Menganalisis dan membandingkan transformasi dan komposisi
transformasi dengan menggunakan matriks.
Indikator : 3.5.1 Menyebutkan contoh translasi, refleksi, rotasi, dan dilatasi dalam
kehidupan sehari-hari.
3.5.2 Menemukan sifat-sifat translasi, refleksi, rotasi, dan dilatasi
berdasarkan pengamatan pada masalah kontekstual dan pengamatan
objek pada bidang koordinat.
3.5.3 Menemukan konsep translasi dengan kaitannya dengan konsep
matriks.
3.5.4 Menemukan konsep refleksi terhadap titik 𝑂(0,0) dengan kaitannya
dengan konsep matriks.
3.5.5 Menemukan konsep refleksi terhadap sumbu x dengan kaitannya
dengan konsep matriks.
3.5.6 Menemukan konsep refleksi terhadap sumbu y dengan kaitannya
dengan konsep matriks.
3.5.7 Menemukan konsep refleksi terhadap garis 𝑦 = 𝑥 dengan kaitannya
dengan konsep matriks.
3.5.8 Menemukan konsep refleksi terhadap garis 𝑦 = −𝑥 dengan kaitannya
dengan konsep matriks.
3.5.9 Menemukan konsep rotasi pada suatu sudut dan pusat 𝑂(0,0) dengan
kaitannya dengan konsep matriks.
3.5.10 Menemukan konsep rotasi pada suatu sudut dan pusat 𝑃(𝑝, 𝑞)

71. No. Dokumen : MA-FR-03-03-05 Tgl. Terbit : 01-01-2019 No. Revisi : 00 Hal :71/71
dengan kaitannya dengan konsep matriks.
3.5.11 Menemukan konsep dilatasi pada faktor skala 𝑘 dan pusat 𝑂(0,0)
dengan kaitannya dengan konsep matriks.
3.5.12 Menemukan konsep dilatasi pada faktor skala 𝑘 dan pusat 𝑃(𝑝, 𝑞)
dengan kaitannya dengan konsep matriks.
3.5.13 Membandingkan keempat jenis transformasi dengan menyebutkan
perbedaannya.
3.5.14 Menemukan konsep komposisi transformasi (translasi, refleksi, rotasi,
dan dilatasi).
KKM : KD 3.5 .....
A. Remedial
No
Nama Peserta
Didik
Nilai Ujian
Harian
Indikator yang
Belum Dikuasai
Bentuk Tindakan
Remedial
Nilai Setelah
Remedial
Ket.
1
2
3
4
5
6
7
8
9
10
11
12
Bagi peserta didik yang belum memenuhi kriteria ketuntasan minimal (KKM), maka pendidik
bisa memberikan soal tambahan berupa ujian kembali atau berupa penugasan.
B. Pengayaan
Pendidik memberikan nasihat agar tetap rendah hati, karena telah mencapai KKM (Kriteria
Ketuntasan Minimal). Pendidik memberikan soal pengayaan berupa soal-soal yang terdapat pada
dokumen UN/SBMPTN yang berkaitan dengan materi yang dipelajari (perbandingan trifonometri
pada segitiga dan relasi sudut).
Ujung, .............................................
Guru Mata Pelajaran,
MUH. ALFIANSYAH, S.Pd., M.Pd.