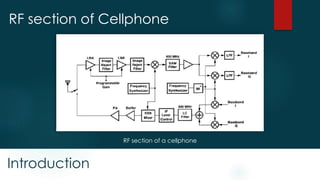
This document provides an introduction to basic RF concepts including nonlinearity, noise, impedance transformation, gain, linearity and time variance, harmonic distortion, gain compression, cross modulation, and intermodulation. It discusses key effects like how nonlinearity can lead to harmonic distortion and intermodulation distortion, and how gain compression occurs when the input power is increased. It also introduces important RF parameters for characterizing devices and circuits like the 1 dB compression point and third order intercept point.

1. RF Microelectronics
CHAPTER- 2: BASIC CONCEPT'S.
BY: AHMED SAKR.
SUPERVISED BY:
PROF. HESHAM HAMED, DR. MAHMOUD A. ABDELGHANY.

2. Introduction
RF section of Cellphone
RF section of a cellphone

3. Introduction
Design bottleneck
RF Section is the bottleneck of wireless
communication systems. Because:
- The performance of the RF front end affects the
overall performance of the entire system.
- RF design involves many disciplines the designer
should understand.
- There are many trade-offs in RF design.
- Relay on experience even while using design tools.
Trade-offs in RF design

4. Basic concepts.
Design bottleneck
Nonlinearity
• Harmonic
distortion.
• Compression.
• Intermodulation.
• Dynamic
nonlinear
systems.
Noise
• Noise Spectrum.
• Device Noise.
• Noise in circuits.
Impedance
Transformation
• Series- Parallel
conversion.
• Matching
networks.
• S-Parameters.

5. Unites in RF
Logarithmic operations review
𝑖𝑓 10 𝐴 = 𝐵 , 𝑡ℎ𝑒𝑛 log 𝐵 = 𝐴
log
1
𝑥
= − log 𝑥
log 10 𝑥 = 𝑥
log 𝑥 𝑎 = 𝑎𝑙𝑜𝑔(𝑥)
log 𝑥𝑦 = log 𝑥 + log 𝑦
log
𝑥
𝑦
= log 𝑥 − log 𝑦

6. Unites in RF
Gain
Rin Rout
Vin Vout
𝑽𝒐𝒍𝒕𝒂𝒈𝒆 𝒈𝒂𝒊𝒏 𝑨 𝒗 =
𝑉𝑜𝑢𝑡
𝑉𝑖𝑛
𝑅𝑀𝑆
𝑷𝒐𝒘𝒆𝒓 𝒈𝒂𝒊𝒏 𝑨 𝑷 =
𝑃𝑜𝑢𝑡
𝑃𝑖𝑛
=
𝑉𝑜𝑢𝑡2
𝑅𝑜𝑢𝑡
𝑉𝑖𝑛2
𝑅𝑖𝑛
=
𝑉𝑜𝑢𝑡2
𝑉𝑖𝑛2
×
𝑅𝑜𝑢𝑡
𝑅𝑖𝑛
= 𝐴𝑣2
×
𝑅𝑜𝑢𝑡
𝑅𝑖𝑛
𝐢𝐟 𝐑𝐨𝐮𝐭 = 𝐑𝐢𝐧 ⇒ 𝐀 𝐏 = 𝐀 𝐯
𝟐

7. Unites in RF
Gain (in dB)
𝒅𝑩 𝑨 𝒗 = 20log(
𝑉𝑜𝑢𝑡
𝑉𝑖𝑛
)
𝒅𝑩 𝑨 𝑷 = 10 log
𝑃𝑜𝑢𝑡
𝑃𝑖𝑛
= 10 log
𝑉𝑜𝑢𝑡2
𝑉𝑖𝑛2
×
𝑅𝑜𝑢𝑡
𝑅𝑖𝑛
𝑠𝑖𝑔𝑛𝑎𝑙 𝑝𝑜𝑤𝑒𝑟| 𝑑𝐵 𝑃𝑠 = 10 log
𝑃𝑠
1𝑚𝑊
→ 𝑖𝑓 𝑅𝑜𝑢𝑡 = 𝑅𝑖𝑛 ⇒ 𝒅𝑩 𝑨 𝒑 = 𝒅𝑩(𝑨 𝒗)
𝑽𝒐𝒍𝒕𝒂𝒈𝒆 𝒈𝒂𝒊𝒏 𝑨 𝒗 =
𝑉𝑜𝑢𝑡
𝑉𝑖𝑛
𝑅𝑀𝑆
𝑷𝒐𝒘𝒆𝒓 𝒈𝒂𝒊𝒏 𝑨 𝑷 =
𝑃𝑜𝑢𝑡
𝑃𝑖𝑛
=
𝑉𝑜𝑢𝑡2
𝑅𝑜𝑢𝑡
𝑉𝑖𝑛2
𝑅𝑖𝑛
=
𝑉𝑜𝑢𝑡2
𝑉𝑖𝑛2
×
𝑅𝑜𝑢𝑡
𝑅𝑖𝑛
= 𝐴𝑣2 ×
𝑅𝑜𝑢𝑡
𝑅𝑖𝑛
→ 𝐢𝐟 𝐑𝐨𝐮𝐭 = 𝐑𝐢𝐧 ⇒ 𝐀 𝐏 = 𝐀 𝐯
𝟐

8. Unites in RF
Voltage gain Vs. power gain
Rin Rout
Vin Vout
We are interested in calculating the output
voltage rather than the output power
when the input and output impedance are
not equal or contain negligible real parts.
Why?
Because the voltage gain is not equal to
the power gain in this case, which is
common in RF design.

9. Linearity and time variance
Linearity
For a linear system, if:
X1(t) → Y1(t) , X2(t) → Y2(t)
aX1(t) + bX2(t) → aY1(t) + bY2(t)
Otherwise, the system is nonlinear.
Time Variance
For a time invariant system, if:
X(t) → Y(t)
Then : X(t-T)→ Y(t-T)
Otherwise, the system is time variant.
What about nonzero initial conditions and
dc offsets? - They are linear too.

10. Linearity and time variance
Switching system
Nonlinear, time variant Linear, time variant

11. Linearity and time variance
Nonlinear, time variant

12. Linearity and time variance
Linear , time variant Vin2 delayed by 45 degree

13. Memory-less systems [outputs don’t depend on past values of
input(s), opposite to Dynamic systems.]
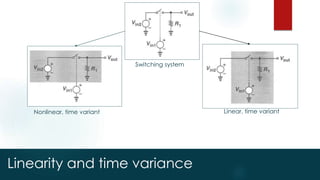
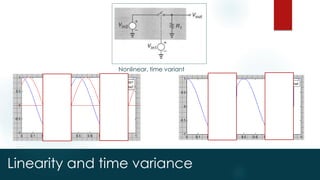
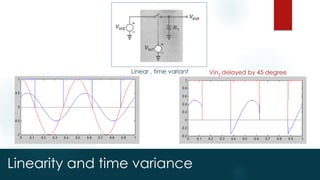
Memory-less linear systems
 y(t) = x(t)
Memory-less nonlinear systems
 y(t) = 1 x(t) + 2 x2(t) + 3 x3(t) +… n xn(t)
If j=0 for even j, the system is said to
have odd symmetry, when his
response to –x(t) is negative to that to
x(t).
The circuit having this property is
called differential or balanced.

14. Nonlinearity effects.
 y(t) = 1 x(t) + 2 x2(t) + 3 x3(t) +… n xn(t)
DC
component
Total
Gain
[compression
@ 1 3 <0]
2nd
harmonic
Suppresse
d for odd
symmetry.
3rd
harmonic
Small
signal
gain

15. Harmonic distortion.
 y(t) = 1 x(t) + 2 x2(t) + 3 x3(t) +… n xn(t)
DC
component
fundamental 2nd
Harmonic
3rd
Harmonic
In many RF designs, the harmonics
distortion is unimportant but should be
tested before they are dismissed, usually
harmonics are filtered, but it is a key
parameter to test the performance of
specific circuits such as Mixers
Common
in
MIXERS
&OSC

16. Gain compression
 y(t) = 1 x(t) + 2 x2(t) + 3 x3(t) +… n xn(t)
DC
component
Total
Gain
[compression
@ 1 3 <0]
2nd
harmonic
Suppresse
d for odd
symmetry.
3rd
harmonic
Small
signal
gain
@ 1 3 <0 the gain is compressed as A rises
1 =500
3 =-0.1

17. Gain compression [1-dB compression point]
@ 1-dB compression point, the gain is
reduced by 10%
Desensitization: when large
interferer [blocker] causes gain
compression while sensing weak
desired signal.
[lowers the SNR]

18. Cross modulation.
 y(t) = 1 x(t) + 2 x2(t) + 3 x3(t) +… n xn(t)
Weak signal + large interferer
large interferer:
Variations in A2 (modulation) affects the
amplitude of the signal (A1) Common
in
AMPLIFIERS

19. Intermodulation.
Intermodulation
components
Fundamental
components

20. Intermodulation.
Third order intermodulation products are the most important. If the difference between w1 and
w2 is small they will appear close to the fundamentals, making it hard to design a filter to
discard the effect of them.
This effect is significant in LNA as shown in next figure…

21. Intermodulation[two-tone test].
Two signals with
small A
is chosen to minimize
nonlinearity effect on it
Gain = 1
Fundamental A
IM products A3
Plot in log-log scale,
the intersection is
the third-order
intercept point
IIP3 is beyond the allowable
input range or even higher
than the supply voltage,
because if the input level
reached the AIP3 the gain
drops and higher order IM
products become significant.

22. Intermodulation[two-tone test].
IIP3 is chosen beyond the allowable
input range or even higher than the
supply voltage, because if the input
level reached the AIP3 the gain drops
and higher order IM products
become significant.
AIIP3 is greater than
the 1-dB compression
point with 9.6 dB

23. IIP3 direct calculation. [two-tone test].

24. Any Questions?