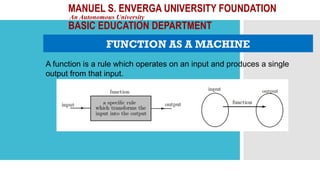
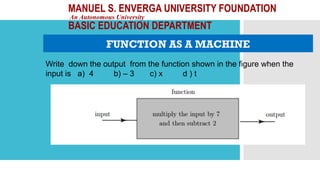
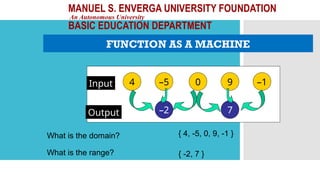
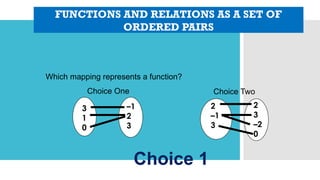
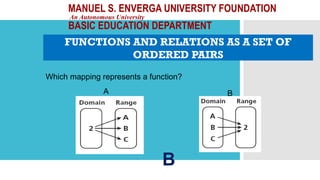
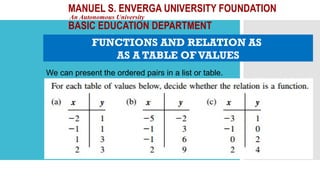
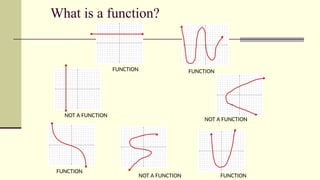
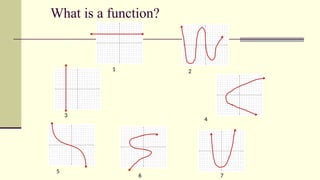
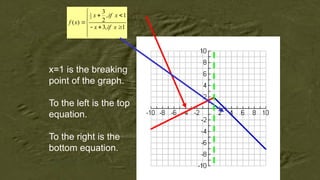
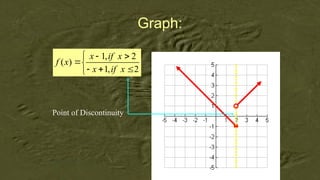
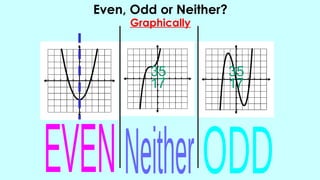
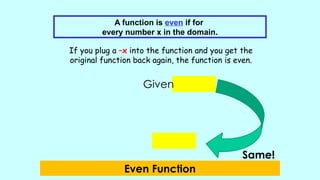
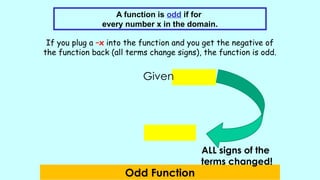
The document outlines activities and standards focused on teaching functions, including identifying functions from graphs, matching functions with their representations, and applying functions to real-life situations. It emphasizes the understanding of function properties, operations, and real-world applications like distance, cost, and piecewise functions. Additionally, it discusses assessment rubrics and common student errors related to functions.




























![Find the Domain and Range of a Relation.
c.
Domain is { x | – 5 ≤ x ≤ 5 }
in set-builder notation
or [ – 5, 5 ] in interval notation
Range is { y | – 3 ≤ y ≤ 4}
in set-builder notation
or [ – 3, 4 ] in interval notation
FUNCTIONS AS A GRAPH IN THE
CARTESIAN PLANE](https://image.slidesharecdn.com/gr-11-genmath-01-functions-240802071555-0b43b43b/85/GENERAL-MATHEMATICS-FOR-GRADE-11-FUNCTIONS-pptx-43-320.jpg)
![Find the Domain and Range of a Relation.
d.
Domain is { x | x ≤ 3 }
in set-builder notation
or (– ∞, 3] in interval notation
Range is in set-builder notation
ℝ
or ( – ∞, ∞ ) in interval notation
Domain is or ( – ∞, ∞ )
ℝ
Range is { y | y ≥ 0 } or ( 0, ∞ )
FUNCTIONS AS A GRAPH IN THE
CARTESIAN PLANE](https://image.slidesharecdn.com/gr-11-genmath-01-functions-240802071555-0b43b43b/85/GENERAL-MATHEMATICS-FOR-GRADE-11-FUNCTIONS-pptx-44-320.jpg)

















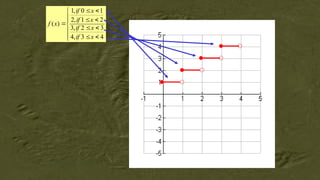

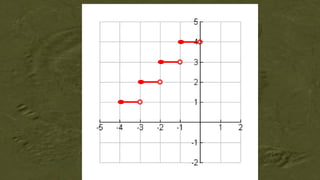

![Special Step Functions
In a floor function, all nonintegers are rounded down to the
nearest integer.
The way we usually count our age is an example of a floor
function since we round our age down to the nearest year and do
not add a year to our age until we have passed our birthday.
The floor function is the same thing as the greatest integer
function which can be written as f (x)=[x].](https://image.slidesharecdn.com/gr-11-genmath-01-functions-240802071555-0b43b43b/85/GENERAL-MATHEMATICS-FOR-GRADE-11-FUNCTIONS-pptx-71-320.jpg)
![MANUEL S. ENVERGA UNIVERSITY FOUNDATION
An Autonomous University
BASIC EDUCATION DEPARTMENT
Greatest integer function: f(x) = [x]
For example:
[2.1] = 2, i.e. greatest integer less than or equal to 2.1 is 2, similarly
[–2.1] = –3
[2] = 2
[3 . 9] = 3
[–3 . 9] = –4
PIECEWISE FUNCTIONS](https://image.slidesharecdn.com/gr-11-genmath-01-functions-240802071555-0b43b43b/85/GENERAL-MATHEMATICS-FOR-GRADE-11-FUNCTIONS-pptx-72-320.jpg)









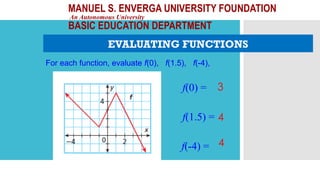
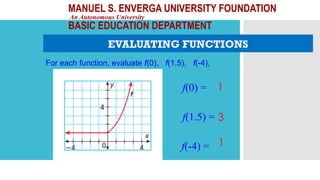
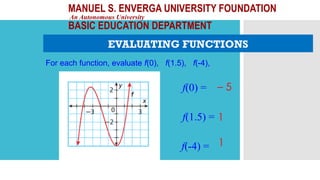
![MANUEL S. ENVERGA UNIVERSITY FOUNDATION
An Autonomous University
BASIC EDUCATION DEPARTMENT
EVALUATING FUNCTIONS
Given f(x) = x2
– 4x + 7 Find.
h
x
f
h
x
f )
(
)
(
h
x
x
h
x
h
x ]
7
4
[
]
7
)
(
4
)
[( 2
2
h
x
x
h
x
h
xh
x 7
4
7
4
4
2 2
2
2
h
h
h
xh 4
2 2
h
h
x
h )
4
2
(
= 2x + h - 4](https://image.slidesharecdn.com/gr-11-genmath-01-functions-240802071555-0b43b43b/85/GENERAL-MATHEMATICS-FOR-GRADE-11-FUNCTIONS-pptx-95-320.jpg)
























