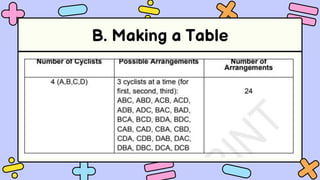
This document discusses different counting techniques including permutation, combination, systematic listing, making tables, tree diagrams, and the fundamental counting principle. It provides examples of how to use each technique to count outcomes. Specifically, it explains that permutation involves order while combination does not, and gives examples of situations that use each. It also works through examples of counting different outfits, ice cream orders, and pizza topping combinations using various counting methods.

1. REVIEW: Permutation VS Combination
How is permutation different from
combination?

2. • the order of
objects
matter
• in exact order
• the order of
objects does
not matter
• in any order
Differences
PERMUTATION COMBINATION

3. REVIEW: Permutation VS Combination
CHECKING OF PREVIOUS ACTIVITY
Directions: Identify if each statement
involves permutation or combination in the
selection of objects.

4. REVIEW: Permutation VS Combination
1. A team of 8 basketball players needs
to choose a captain and co-captain.
PERMUTATION

5. REVIEW: Permutation VS Combination
2. Rob and Mary are planning trips to
nine countries this year. There are 13
countries they would like to visit. They
are deciding which countries to skip.
COMBINATION

6. REVIEW: Permutation VS Combination
3. The batting order for seven players
on a 12-person team.
COMBINATION

7. REVIEW: Permutation VS Combination
4. There are 45 applicants for three
Computer Programmer positions.
COMBINATION

8. REVIEW: Permutation VS Combination
5. Castel and Joe are planning trips to
three countries this year. There are 7
countries they would like to visit. One
trip will be one week long, another two
days, and the other two weeks.
PERMUTATION

9. Counting
Techniques
Prepared by MS. RIGEN V. MAALAM

10. Example of an event
There are 4 cyclists in a race.
In how many ways will they be ranked as
first, second, and third placers?
Let the cyclists be named as A, B, C and D.

11. Counting Techniques
a. Systematic Listing
b. Making a Table
c. Tree Diagram
d. Fundamental Counting
Principle
Tip: Use links to go to a different page
inside your presentation. Links work
best for pages like this one!
How: Highlight text, click on the link
symbol on the toolbar, and select the
page in your presentation that you
want to connect.

12. A. Systematic Listing
Systematic listing is a counting technique
that involves a complete list of all possible
outcomes.

13. A. Systematic Listing

14. B. Making a Table
Making a table is a technique where
values or different possibilities are
tabulated.

15. B. Making a Table

16. C. Tree Diagram
Tree diagram is a counting technique
which uses line segments originating from
an event to an outcome. This is a picture
of all possible outcomes when an event is
unfolded.

17. C. Tree Diagram

18. D. Fundamental Counting Principle
• Also known as the Basic Counting Principle
• States that...
"when there are m ways to do one thing, and n
ways to do another, then there are (m)(n) ways
of doing both".

19. D. Fundamental Counting Principle
first placer second placer third placer
4 cyclist 3 cyclist 2 cyclist
= 4 x 3 x 2 = 24 possible arrangements

20. Counting Techniques
a. Systematic Listing
b. Making a Table
c. Tree Diagram
d. Fundamental Counting
Principle
Tip: Use links to go to a different page
inside your presentation. Links work
best for pages like this one!
How: Highlight text, click on the link
symbol on the toolbar, and select the
page in your presentation that you
want to connect.

21. 2. There are 6 flavors of ice-cream, and 3
different cones. How many different
single-scoop ice-creams you could order?
More examples...
1. You have 3 shirts and 4 pants.
How many different outfits van you make?

22. 2. There are 6 flavors of ice-cream, and 3
different cones. That means 6×3=18
different single-scoop ice-creams you
could order.
Answers...
1. You have 3 shirts and 4 pants.
That means 3×4=12 different outfits.

23. Directions: In a 1/4 sheet of paper, solve
for what is asked in the following problem.
Show your solution using the following
counting techniques:
a. Tree Diagram
b. Fundamental Counting Principle
Seatwork

24. Sarah goes to her local pizza parlor and
orders a pizza. She can choose either a
large or a medium pizza, can choose one
of seven different toppings, and can have
three different choices of crust. How many
different pizzas could Sarah order?
Seatwork