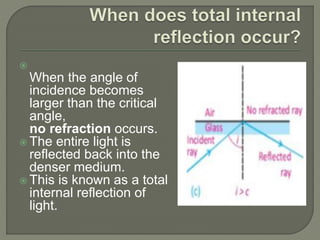
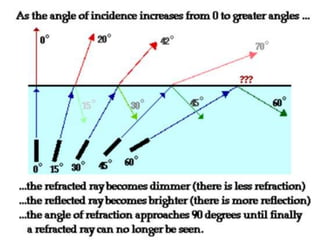
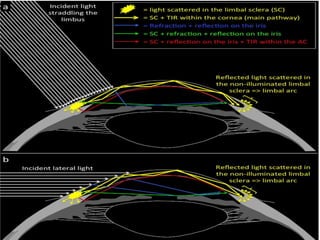
The document explains the phenomenon of refraction and total internal reflection of light when transitioning between media of different densities. It discusses the critical angle, which is the angle of incidence that results in a 90-degree refraction angle, and outlines conditions necessary for total internal reflection to occur. Additionally, it provides a mathematical example to calculate the critical angle for a scuba diver's light underwater.

1. Prepared by:
Jenno S. Lantaya, OD

2.  When a ray of light traveling in the denser
medium enters into a rarer medium, it bends
away from the normal.
 If the angle of incidence ‘i’ increases’ the
angle of refraction ‘r’ also increases.
 For a particular value of the angle of
incidence, the angle of refraction becomes
90°.
 The angle of incidence, that cause the
refracted ray in the rarer medium to bend
through 90° is called critical angle.

3. 
When the angle of
incidence becomes
larger than the critical
angle,
no refraction occurs.
 The entire light is
reflected back into the
denser medium.
 This is known as a total
internal reflection of
light.

5.  TIR only takes place when both of the
following two conditions are met
• the light is in the more dense medium and
approaching the less dense medium.
• the angle of incidence is greater than the so-called
critical angle.

6. The maximum possible angle of refraction
is 90-degrees.
So in the case of the laser beam in the
water, there is some specific value for the
angle of incidence (we'll call it the critical
angle) that yields an angle of refraction of
90-degrees.

8. Optical fibres
Endoscope
Periscope
Binoculars
Prisms
Sclerotic scatter
illumination of the
eye

10.  This is the angle of incidence that provides
an angle of refraction of 90-degrees.
 it is the largest angle of incidence for which
refraction can still occur.

11. nsini= n’sin90
Where:
n= index of refraction of medium of incidence
n’= index of refraction of medium of refraction
i= angle of incidence
90= constant angle of refraction

12.  1. A scuba diver shines a light underwater and
enters the boundary of air. What is the critical
angle?
• Given:
 n= 1.33 (water)
 n’= 1.0 (air)
 90 degrees= constant
 sin i=?
Solution:
nsini= n’sin90
1.33 sin i= 1.0 sin 90
1.33 sin i= 1.0 (1)
1.33 sin 𝑖
1.33
=
1
1.33
Sin i= 0.751879699
= 48.75346663
i= 48 degrees 45 minutes 12.48 seconds