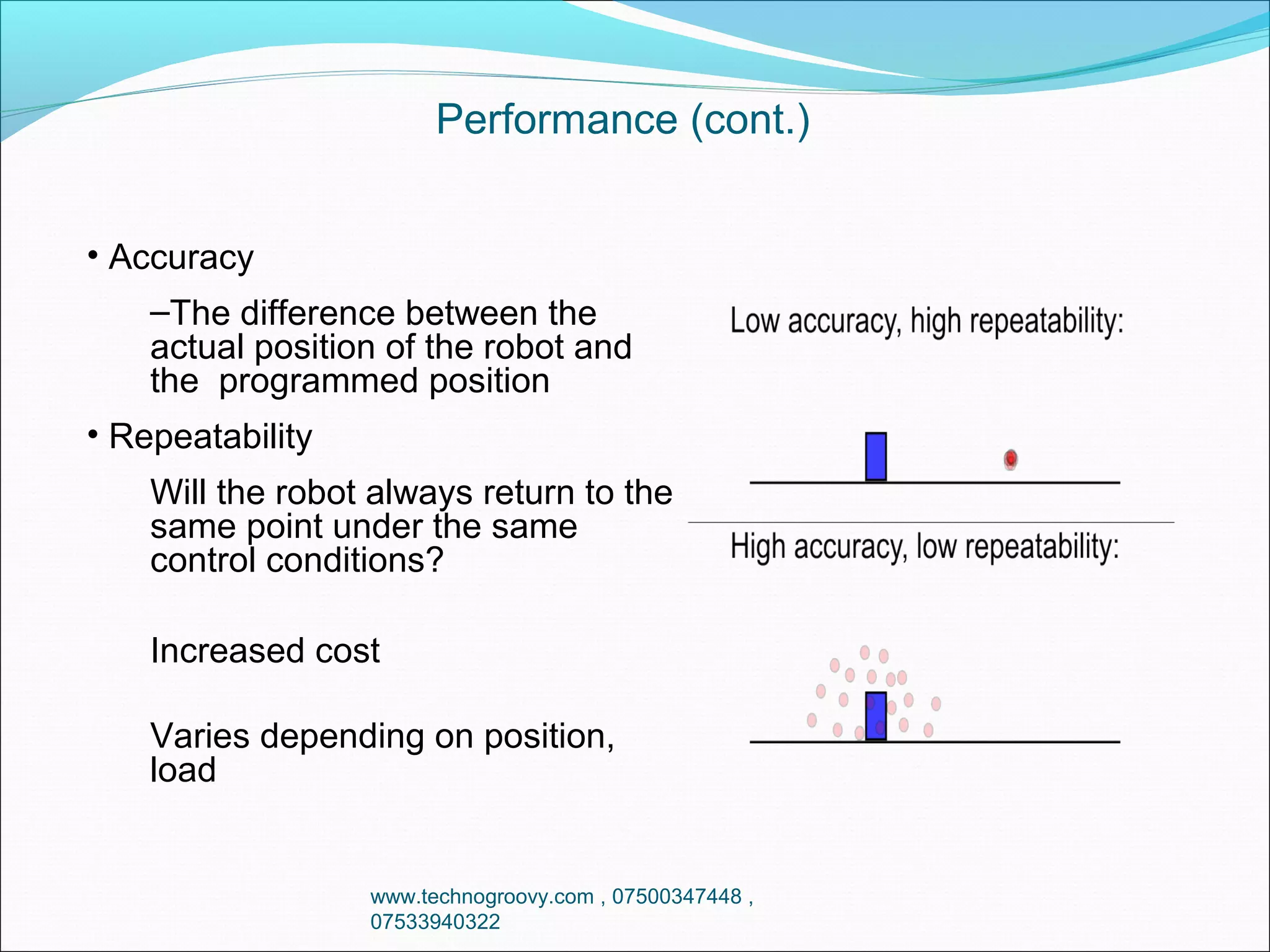
The document provides an overview of robots, defining them as machinery capable of performing various tasks such as dangerous operations, assembly line work, and precision machining. It discusses different types of robots, their control mechanisms, kinematics, dynamics, and performance measures, including accuracy and repeatability. Additionally, it touches on programming challenges and innovations in robotics, such as haptic feedback and robots capable of learning.

1. www.technogroovy.com , 07500347448 ,07533940322

2. Definition:
Alternate definition:
“A robot is a one-armed, blind idiot with limited memory
and which cannot speak, see, or hear.”
www.technogroovy.com , 07500347448 ,
07533940322

3. Ideal Tasks
Tasks which are:
 Dangerous
 Space exploration
 chemical spill cleanup
 disarming bombs
 disaster cleanup
 Boring and/or repetitive
 Welding car frames
 part pick and place
 manufacturing parts.
 High precision or high speed
 Electronics testing
 Surgery
 precision machining.
www.technogroovy.com , 07500347448 ,
07533940322

4. Automation vs. robots
Automation –Machinery designed
task
to carry out a specific
 Bottling machine
 Dishwasher
 Paint sprayer
Robots – machinery designed
to carry out a variety of tasks
 Pick and place arms
 Mobile robots
 Computer Numerical Control
machines
www.technogroovy.com , 07500347448 ,
07533940322

5. Types of robots
Pick and place
Moves items between points
Continuous path control
Moves along a programmable path
Sensory
Employs sensors for feedback
www.technogroovy.com , 07500347448 ,
07533940322

6. Pick and Place
 Moves items from one point to
another
 Does not need to follow a specific
path between points
 Uses include loading and unloading
machines, placing components on
circuit boards, and moving parts off
conveyor belts.
www.technogroovy.com , 07500347448 ,
07533940322

7. Continuous path
control
Moves along a specific
path
Uses include welding,
cutting, machining parts.
www.technogroovy.com , 07500347448 ,
07533940322

8. Sensory
Uses sensors for feedback.
Closed-loop robots use sensors
in conjunction with actuators
to gain higher accuracy – servo
motors.
Uses include mobile robotics,
telepresence, search and
rescue, pick and place with
machine vision.
www.technogroovy.com , 07500347448 ,
07533940322

9. Measures of
performance
 Working volume
 The space within which the robot operates.
 Larger volume costs more but can increase the capabilities
of a robot
 Speed and acceleration
 Faster speed often reduces resolution or increases cost
 Varies depending on position, load.
 Speed can be limited by the task the robot performs
(welding, cutting)
 Resolution
 Often a speed tradeoff
 The smallest step the robot can take
www.technogroovy.com , 07500347448 ,
07533940322

10. Performance (cont.)
• Accuracy
–The difference between the
actual position of the robot and
the programmed position
• Repeatability
Will the robot always return to the
same point under the same
control conditions?
Increased cost
Varies depending on position,
load
www.technogroovy.com , 07500347448 ,
07533940322

11. Control
•Open loop, i.e., no feedback, deterministic
•Closed loop, i.e., feedback, maybe a sense of
touch and/or vision
www.technogroovy.com , 07500347448 ,
07533940322

12. Kinematics and dynamics
Degrees of freedom—number of independent
motions
Translation--3 independent directions
Rotation-- 3 independent axes
2D motion = 3 degrees of freedom: 2 translation, 1
rotation
3D motion = 6 degrees of freedom: 3 translation, 3
rotation
www.technogroovy.com , 07500347448 ,
07533940322

13. Kinematics and dynamics (cont.)
Actions
Simple joints
prismatic—sliding joint, e.g., square cylinder in square tube
 revolute—hinge joint

Compound joints
ball and socket = 3 revolute joints
 round cylinder in tube = 1 prismatic, 1 revolute

Mobility
Wheels
multipedal (multi-legged with a sequence of actions)
www.technogroovy.com , 07500347448 ,
07533940322

14. Kinematics and dynamics (cont.)
Work areas
rectangular (x,y,z)
cylindrical (r,θ,z)
x'
x''
x
spherical (r,θ,ϕ)
Coordinates
World coordinate frame
End effector frame

How to get from coordinate system x” to x’ to x
www.technogroovy.com , 07500347448 ,
07533940322

15. Transformations
General coordinate transformation from x’ to x is x = Bx’
+ p , where B is a rotation matrix and p is a translation
vector
More conveniently, one can create an augmented matrix
which allows the above equation to be expressed as x = A
x’.
Coordinate transformations of multilink systems are
represented as
x0 = A01 A12A23. . .A(n-1)(n)xn
www.technogroovy.com , 07500347448 ,
07533940322

16. Dynamics
Velocity, acceleration of end actuator
power transmission
actuator
solenoid –two positions , e.g., in, out
 motor+gears, belts, screws, levers—continuum of positions
 stepper motor—range of positions in discrete increments

www.technogroovy.com , 07500347448 ,
07533940322

17. A 2-D “binary” robot segment

Example of a 2D robotic link having three
solenoids to determine geometry. All members are
linked by pin joints; members A,B,C have two states—
in, out—controlled by in-line solenoids. Note that
the geometry of such a link can be represented in
terms of three binary digits corresponding to the
states C A,B,C, e.g., 010 represents A,C in, B out.
of A B C
A
B
B
A
C
A
B
C
Links can be chained together and controlled by sets
of three bit codes.
A
B
C
A
B
C
A
B
C
www.technogroovy.com , 07500347448 ,
07533940322
A
B
C

18. Problems
Joint play, compounded through N joints
Accelerating masses produce vibration, elastic
deformations in links
Torques, stresses transmitted depending on end
actuator loads
www.technogroovy.com , 07500347448 ,
07533940322

19. Control and programming
Position of end actuator
 multiple solutions
Trajectory of end actuator: how to get from point A to B
 programming for coordinated motion of each link
 problem—sometimes no closed-form solution
www.technogroovy.com , 07500347448 ,
07533940322

20. Control and programming (cont.)
Example: end actuator (tip) problem with no closed solution.
Two-segment arm with arm lengths L1 = L2, and stepper -motor
control of angles θ1 and θ2.
L
2
y
θ2
L1
θ1
Problem: control θ1 and θ2 such that arm tip traverses its range
at constant height y, or with no more variation than δy.
Geometry is easy: position of arm tip
x = L1 (cos θ1 + cos θ2)
y = L1 (sin θ1 + sin θ2)
www.technogroovy.com , 07500347448 ,
07533940322

21. Control and programming (cont.)
Arm tip moves by changing θ1 and θ2 as a function of time.



x = − L1 (sin θ1 θ1 + sin θ 2 θ 2 )
Therefore



y = L1 (cos θ1 θ1 + cos θ 2 θ 2 ) = 0
So, as θ1 and θ2 are changed, x and y θ = affected.1
are −θ cos θ


2
1
cos θ 2
To satisfy y = constant, we must have
. So the rates at which θ1 and θ2 are changed depend on the
values of θ1 and θ2.
www.technogroovy.com , 07500347448 ,
07533940322

22. Control and programming (cont.)
There is no closed-form solution to this problem. One must use
approximations, and accept some minor variations in y. Moving the
arm tip through its maximum range of x might have to be
accomplished through a sequence of program steps that define
different rates of changing θ1 and θ2.
 Possible approaches:
 Program the rates of change of θ1 and θ2 for y = const. for initial values
of θ1 and θ2 . When arm tip exceeds δy, reprogram for new values of θ1
and θ2.
 Program the rates of change of θ1 and θ2 at the initial point and at some
other point for y = const. Take the average of these two rates, and
hope that δy is not exceeded. If it is exceeded, reprogram for a shorter
distance. Continue program segments until the arm tip has traversed
its range.

www.technogroovy.com , 07500347448 ,
07533940322

23. Control and programming (cont.)
 Program the rates of change of θ1 and θ2 at the initial point
and at some other point for y = const. Take the average of
these two rates, and hope that δy is not exceeded. If it is
exceeded, reprogram for a shorter distance. Continue
program segments until the arm tip has traversed its range.
 The rate of change of θ1 and θ2 can be changed in a
programming segment, i.e., the rates of change need not be
uniform over time. This programming strategy incorporates
approaches 1) and 2). Start with rates of change for the
initial values of θ1 and θ2 , then add an acceleration
component so that y = const. will also be satisfied at a
www.technogroovy.com , 07500347448 ,
distant position.
07533940322

24. Feedback
control
Rotation encoders
Cameras
Pressure sensors
Temperature sensors
Limit switches
Optical sensors
Sonar
www.technogroovy.com , 07500347448 ,
07533940322

25. New directions
• Haptics--tactile sensing
• Other kinematic mechanisms,
e.g. snake motion
• Robots that can learn
www.technogroovy.com , 07500347448 ,
07533940322

26. Thank You
Techogroovy Systems India Pvt Ltd
Embedded Systems & Robotics Projects Based Training
www.technogroovy.com
Mail : technogroovy@gmail.com
Cell- +91-7500347448 ,
+91-7533940322
www.technogroovy.com , 07500347448 ,
07533940322