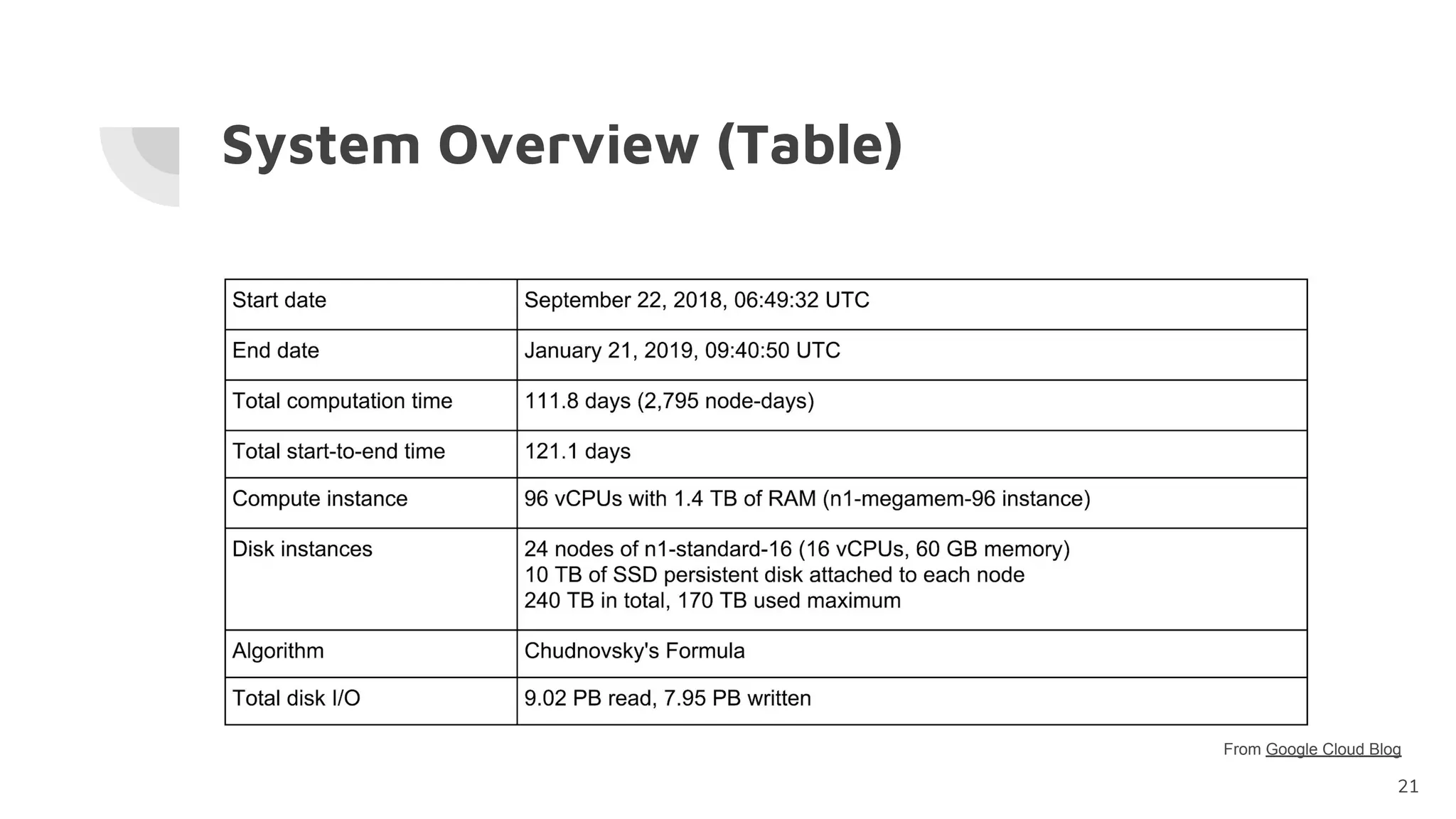
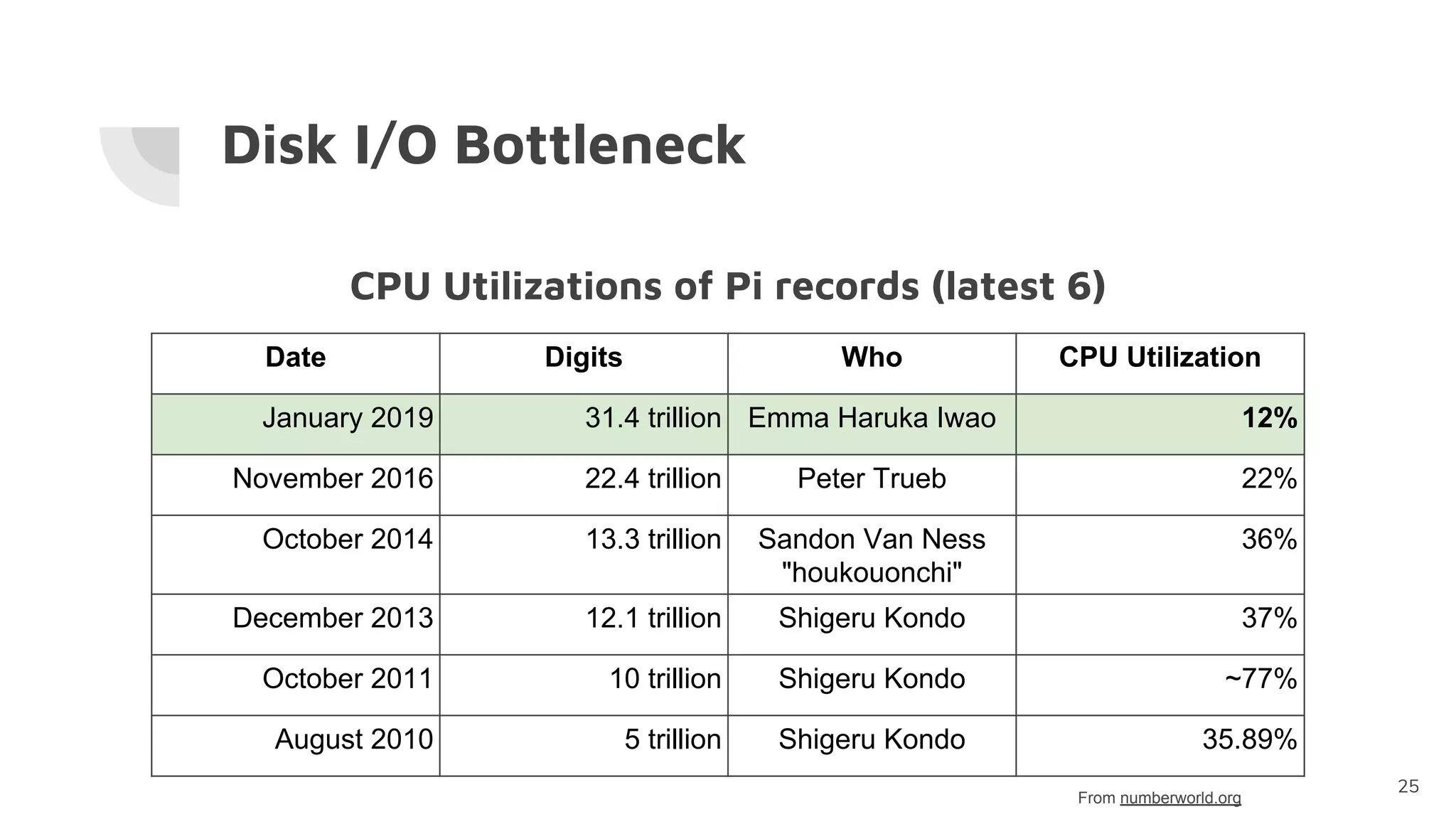
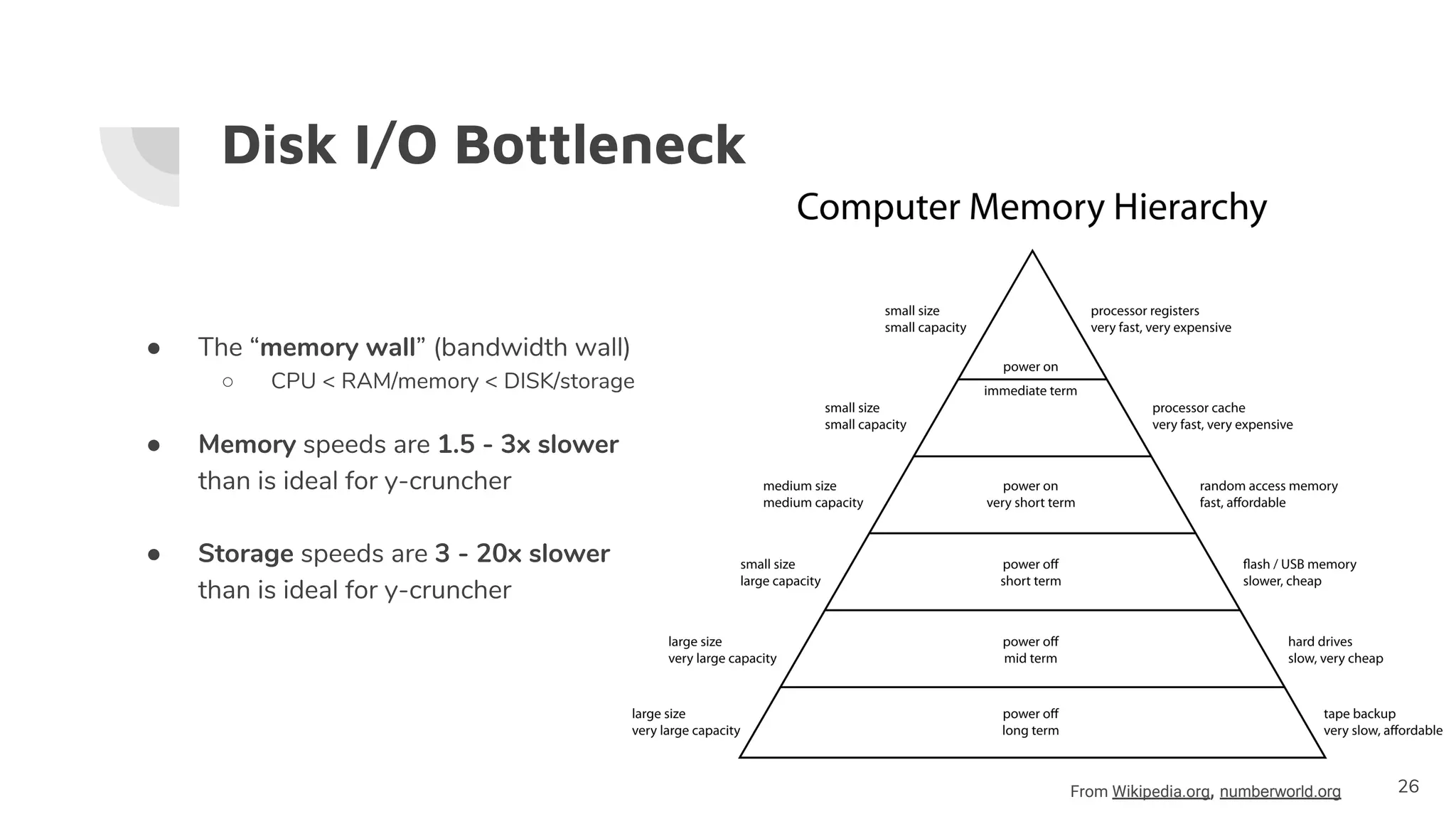
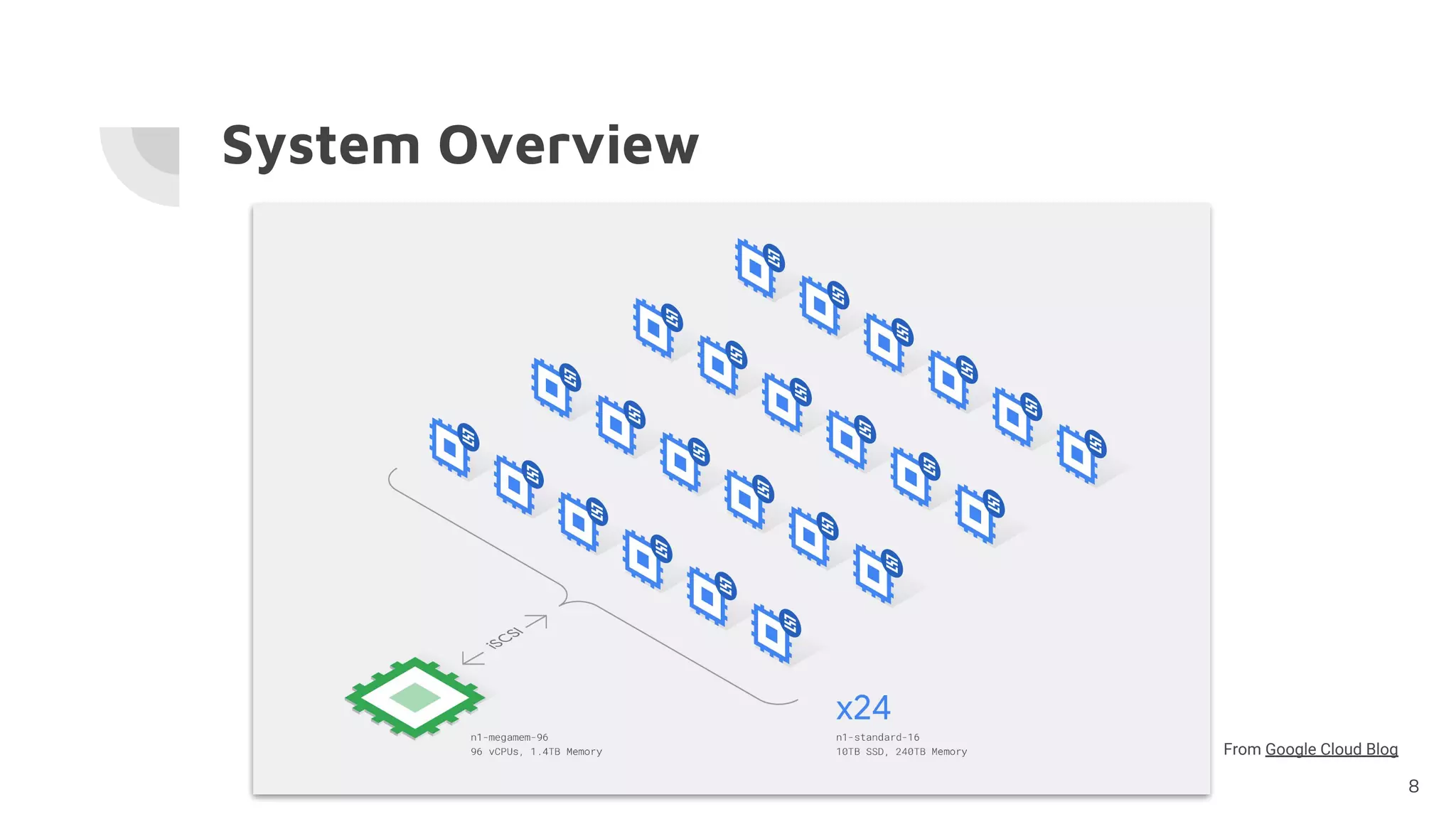
The document discusses the successful computation of pi to a record-breaking 31.4 trillion decimal digits using 'y-cruncher' on Google Cloud, taking 121 days and highlighting the challenges related to storage bandwidth and error detection. Key contributors included Emma Haruka Iwao and Alexander J. Yee, who faced difficulties such as hardware errors and load imbalances during computation. The findings underscore the importance of storage bandwidth and error detection in long-duration computations, acknowledging limitations in error coverage.

1. Reading:
“Pi in the sky: Calculating a
record-breaking 31.4 trillion
digits of Archimedes’ constant
on Google Cloud”
Journal Club at AIS Lab. on April 22, 2019
Kento Aoyama, Ph.D Student
Akiyama Laboratory, Dept. of Computer Science, Tokyo Institute of Technology

2. Outline
1. Abstract
2. Introduction
3. About “y-cruncher” and Pi computation
4. Computational Details
a. System Overview
b. Major Difficulties
c. Minor Difficulties
5. Summary
6. Supplementals
2

3. TL;DR Abstract
3
● Authors successfully computed the Pi to 31.4 trillion decimal digits using "y-cruncher"
which implementing the Chudnovsky formula
● Compute instances provided by Google Cloud were used during 121 days calculation
● Storage bandwidth is the most important
● Error detection and checkpoint/restart functions are crucial for Pi computation

4. The persons who related to the record
● Emma Haruka Iwao (@Yuryu)
○ Pi record holder (31.4 trillion)
○ Developer Advocate for Google Cloud Platform (2015~)
○ M.Sc in Computer Science at University of Tsukuba (Prof. Tatebe Lab.)
● Alexander J. Yee (@Mysticial)
○ Author of “y-cruncher” (the program used for this computation)
○ Software Developer at Citadel LLC (2016~)
○ M.Sc in Computer Science at University of Illinois
○ More details in (numberworld.org)
4

5. Sources of This Presentation
● Google Cloud Blog:
○ ”Pi in the sky: Calculating a record-breaking 31.4 trillion digits of Archimedes’ constant on
Google Cloud” (accessd: April 18, 2019)
● Private Tech Blog (numberworld.org):
○ ”Google Cloud Topples the Pi Record” (accessd: April 18, 2019)
○ “y-cruncher - A Multi-Threaded Pi-Program” (accessd: April 18, 2019)
● Developer Keynote (Google Cloud Next’19):
○ Video: https://www.youtube.com/watch?time_continue=2971&v=W16iHlo2TuE (accessd: April
18, 2019)
● F. Bellard, “Computation of 2700 billion decimal digits of Pi using a Desktop Computer Evaluation of
the Chudnovsky series,” Computer (Long. Beach. Calif)., vol. 2010, pp. 1–11, 2010.
5

6. Introduction
6

7. Rough Introduction
● Most scientific applications don’t need Pi beyond a few hundred digits, but that isn’t
stopping anyone.
● The complexity of Chudnovky's formula - a common algorithm for computing pi - is
O(n (log n)^3): the time and resources necessary to calculate digits increase more
rapidly than the digits themselves
● Using Compute Engine, Google Cloud’s high-performance infrastructure as a service
offering, has a number of benefits over using dedicated physical machines
○ live migration feature lets your application continue running while Google takes care of the
heavy lifting needed to keep our infrastructure up to date
7
From Google Cloud Blog

8. System Overview
8
From Google Cloud Blog

9. Miscellaneous Facts and Statistics
● First Pi record using Cloud Service
● First Pi record using SSD
● First Pi record using AVX512 instruction set
● First Pi record using network attached storage (NAS)
● Second Pi record done with y-cruncher that has encountered/recovered from a silent
hardware error
● The computation racked up a total of 10 PB of file reads, 9 PB of file writes
● The speed of this computation was 1/8 bottlenecked by the storage bandwidth
9
From numberworld.org

10. About “y-cruncher” and
Pi computation
10

11. About y-cruncher
“The first scalable multi-threaded Pi-benchmark for multi-core systems”
● It is developed by Alexander J. Yee (@Mysticial)
● It has been used for 6 world Pi records (April 2019)
● It can be downloaded from webpage ( http://www.numberworld.org/y-cruncher/ )
● It is closed source (few parts of code is available on GitHub with licenses)
● It supports both Windows and Linux systems
11
From numberworld.org

12. Software Features
● Able to compute Pi and other constants to trillions of digits
● Two algorithms are available for most constants: computation and verification
● Multi-Threaded - Multi-threading can be used to fully utilize modern multi-core
processors without significantly increasing memory usage
● Vectorized - Able to fully utilize the SIMD capabilities for most processors (SSE, AVX,
AVX512, etc...)
● Swap Space - management for large computations that require more memory than
there is available
● Multi-Hard Drive - Multiple hard drives can be used for faster disk swapping
● Semi-Fault Tolerant - Able to detect and correct for minor errors that may be caused
by hardware instability or software bugs
12
From numberworld.org

13. Implementation (as of v0.7.7)
General Information:
● y-cruncher started off as a C99 program.
Now it is mostly C++11 with a tiny bit of
C++14
● Intel SSE and AVX compiler intrinsics are
heavily used
● Some inline assembly is used
● C++ template metaprogramming is used
extensively to reduce code duplication
13
Libraries and Dependencies:
● WinAPI (Windows Only)
● POSIX (Linux Only)
● Cilk Plus
● Thread Building Blocks (TBB)
y-cruncher has no other non-system
dependencies. No Boost. No GMP.
From numberworld.org

14. Formulas and Algorithms
y-cruncher provides two algorithms for each major constant: computation and verification
List of available constants (see more detail in numberworld.org/Formulas and Algorithms)
○ Square Root of n and Golden Ratio
○ e - the Napier's constant
○ Pi - the Archimedes’ constant
○ ArcCoth(n) - Inverse Hyperbolic Cotangent
○ Log(n)
○ Zeta(3) - Apery's Constant
○ Catalan's Constant
○ Lemniscate
○ Euler-Mascheroni Constant
14

15. Pi Computation - Chudnovsky formula[a]
with A = 13591409, B = 545140134, C = 640320
Every iteration in the n loop, the generated Pi digits is increased by 14 digits.
“It was evaluated with the binary splitting algorithm. The asymptotic running time is O( M(n)
log(n)^2 ) for a n limb result. It is worst than the asymptotic running time of the
Arithmetic-Geometric Mean algorithms of O(M(n) log(n)) , but it has better locality and many
improvements can reduce its constant factor.” [b]
15
[b] F. Bellard, “Computation of 2700 billion decimal digits of Pi using a Desktop Computer Evaluation of
the Chudnovsky series,” Computer (Long. Beach. Calif)., vol. 2010, pp. 1–11, 2010.
[a] D. V. Chudnovsky and G. V. Chudnovsky, “Approximations and complex multiplication according to
Ramanujan, in Ramanujan Revisited,” Academic Press Inc., Boston, p. 375-396 & p. 468-472, 1988.

16. Binary Splitting Algorithm (1/N)
Let S be defined as
We define the auxiliary integers
16
F. Bellard, “Computation of 2700 billion decimal digits of Pi using a Desktop Computer Evaluation of the
Chudnovsky series,” Computer (Long. Beach. Calif)., vol. 2010, pp. 1–11, 2010.

17. Binary Splitting Algorithm (2/N)
P, Q and T can be evaluated recursively with the following relations defined with
m such as n1
< m < n2
:
17
F. Bellard, “Computation of 2700 billion decimal digits of Pi using a Desktop Computer Evaluation of the
Chudnovsky series,” Computer (Long. Beach. Calif)., vol. 2010, pp. 1–11, 2010.

18. Binary Splitting Algorithm (3/N)
Algorithm 1 is deduced from these relations.
18
For the Chudnovsky series we can take:
We get then
F. Bellard, “Computation of 2700 billion decimal digits of Pi using a Desktop Computer Evaluation of the
Chudnovsky series,” Computer (Long. Beach. Calif)., vol. 2010, pp. 1–11, 2010.

19. Points of the Bellard’s paper
● Precomputed powers
Several constant factors can be precomputed separately, it can reduce the calculations
by using reasonable additional memory
● Multi-threading
Different parts of the binary splitting recursion can be executed in different threads
● Restartability
If operands are stored on disk, each step of computation is implemented so that it is
restartable.
● Fast multiplication algorithm using DFT
19
Because the "y-cruncher" is closed-source and not published ...
Let's refer to the Bellard’s paper which implements the same formula.
F. Bellard, “Computation of 2700 billion decimal digits of Pi using a Desktop Computer Evaluation of the
Chudnovsky series,” Computer (Long. Beach. Calif)., vol. 2010, pp. 1–11, 2010.

20. Computational Details
of the record
20

21. System Overview (Table)
21
From Google Cloud Blog

22. Instance
We selected an n1-megamem-96 instance for the main computing node.
● It was the biggest virtual machine type available on Compute Engine that provided
Intel Skylake processors at the beginning of the project
● The Skylake generation of Intel processors supports AVX-512, which are 512-bit SIMD
extensions - that can perform floating point operations on 512-bit data or eight
double-precision floating-point numbers at once
22
From Google Cloud Blog

23. Storage
We selected n1-standard-16 for the iSCSI target machines to ensure sufficient bandwidth
between the computing node and the storage:
● the network egress bandwidth and Persistent Disk throughput are determined by the
number of vCPU cores
● We used the iSCSI protocol to remotely attach Persistent Disks to add additional
capacity
● The number of nodes were decided based on y-cruncher's disk benchmark
performance
Currently, each Compute Engine virtual machine can mount up to 64 TB of Persistent Disks.
23
From Google Cloud Blog

24. Major Difficulties
24

25. Disk I/O Bottleneck
25
Date Digits Who CPU Utilization
January 2019 31.4 trillion Emma Haruka Iwao 12%
November 2016 22.4 trillion Peter Trueb 22%
October 2014 13.3 trillion Sandon Van Ness
"houkouonchi"
36%
December 2013 12.1 trillion Shigeru Kondo 37%
October 2011 10 trillion Shigeru Kondo ~77%
August 2010 5 trillion Shigeru Kondo 35.89%
CPU Utilizations of Pi records (latest 6)
From numberworld.org

26. Disk I/O Bottleneck
● The “memory wall” (bandwidth wall)
○ CPU < RAM/memory < DISK/storage
● Memory speeds are 1.5 - 3x slower
than is ideal for y-cruncher
● Storage speeds are 3 - 20x slower
than is ideal for y-cruncher
26From Wikipedia.org, numberworld.org

27. Disk I/O Bottleneck
● In this latest Pi computation, the disk/storage bandwidth was about 2-3 GB/s, which
led to an average CPU utilization of 12.2%. ( = about an 1/8 bottleneck)
● If we have infinite storage bandwidth:
○ The computation would have taken 2 ~ 3 weeks (122 * 1/8)
● If we have infinite computational power:
○ The computation would still have taken around 4 month
27
From numberworld.org

28. Network bandwidth (I/O) Bottleneck
● The storages are attached as NAS (Network Attached Storage)
○ “network storage bandwidth” is the limitation factor
● For more details:
○ “Write bandwidth” was artificially capped to about 1.8 GB/s by the platform
○ “Read bandwidth”, while not artificially capped, was still limited to about 3.1 GB/s by the
network hardware
● But, put it simply, 2-3 GB/s is not enough
○ Computation is effectively free: computational improvements by both of software and hardware
■ AVX512. Skylake architecture, etc.
○ GPUs aren't going to help with this kind of storage bottleneck (so there is no GPU versions)
28
From numberworld.org

29. Network bandwidth (I/O) Bottleneck
● We need upward of 20 GB/s of storage bandwidth for the case in high-end server
○ 20 GB/s is less than 2 x PCIe 3.0 x 16 slots, it’s technically possible
○ but it requires a level of hardware customization that we have yet to see
● if we had 20 GB/s of storage bandwidth, the computation would likely have taken
less than 1 month
● Thus in the current era, whoever has the biggest and fastest storage (without
sacrificing reliability) will win the race for the most digits of Pi
29
From numberworld.org

30. Machine Errors on Pi computation
“This computation is the 6th time that y-cruncher has been used to set the Pi record.
It is the 4th time that featured at least one hardware error, and the 2nd that had a
suspected silent hardware error.
Hardware errors are a thing - even on server grade hardware.”
30
From numberworld.org

31. Normal (non-silent) Hardware Errors
Normal (non-silent) hardware errors: not a problem
● The machine crashes, reboot it and resume the computation.
● Circuit breaker trips, turn it back on and resume the computation.
● Hard drive fails, restore from backup and resume the computation…
This is (mostly) a solved problem thanks to checkpoint-restart.
31
From numberworld.org

32. Silent Hardware Errors
Silent hardware errors: a fearful problem
● they are silent and do not cause a visible error
● they lead to data corruption which can propagate to the end of a long computation
resulting in the wrong digits
○ This is the worst scenario because you end up wasting a many-months long computation and
have no idea whether the error was a hardware fault or a software bug ...
32
From numberworld.org

33. Error Detection
● y-cruncher has many forms of built-in error-detection that catch errors as soon as
possible to minimize the amount of wasted resources as well as minimizing the
probability that a computation finishes with the wrong results
● Error-detection saved the 2nd and 4th of hardware error from the bad ending. (in
previous records)
33
From numberworld.org

34. Limitation of Error Detection
Y-cruncher’s error detection only has about 90 % coverage
● Empirical evidence from: actual (unintended) hardware errors, artificially induced errors
by means of overclocking
● Meaning that 1 in 10 silent hardware errors will go undetected and lead the
computation finishing with the wrong digits
● The two errors that have happened so far were both lucky to land in that 90%.
○ The current 10% without coverage is the long tail of code that is either very difficult to do
error-detection, or would incur an unacceptably large performance overhead
34
From numberworld.org

35. Silent Hardware Errors is most fearful
For example:
1. Someone invests a large amount of time and money into a large computation. The digits don't
pass verification.
2. The person contacts me asking for help. But I can't do anything. All that investment is lost.
3. Lot of distress on both sides. Maybe lots of finger-pointing.
For this reason, I typically discourage people from running computations that may take longer
than 6 months.
y-cruncher is currently 6/6 in world record Pi attempts that have run to completion.
But there is some amount of luck to this.
35
From numberworld.org

36. Minor Difficulties
36

37. Load Imbalance with Thread Building
Blocks (TBB)
y-cruncher lets the user choose a parallel computing framework (None, C++11 std::async(),
Thread Spawn, Windows Thread Pool, Push Pool, Cilk Plus, Thread Building Block)
For this computation, we decided to use Intel's Thread Building Blocks (TBB).
But it turned out that TBB suffers severe load-balancing issues under y-cruncher's workload.
By comparison both Intel's own Cilk Plus and y-cruncher's Push Pool had no such problems.
The result was a loss of computational performance.
In the end, this didn't matter since the disk bottleneck easily absorbed any amount of
computational inefficiency.
37
From numberworld.org

38. Deployment Issues
There were numerous issues with deployment. Examples include:
● The were performance issues with live migration due to the memory-intensiveness of
the computation (The 1.4 TB of memory would have been completely overwritten
roughly once every ~10 min. for much of the entire computation)
● There were timeout issues with accessing the external storage nodes
38
From numberworld.org

39. Summary
39

40. Summary
40
● Authors successfully computed the Pi to 31.4 trillion decimal digits using "y-cruncher"
which implementing the Chudnovsky formula
● Compute instances (1 fat-compute node with 24 storage-node) provided by Google
Cloud were used during 121 days calculation
● Storage bandwidth is the most important: as the limitation factor of computation
performance is the bandwidth of network attached storage so that the average CPU
utilization was 12%
● Error detection and checkpoint/restart functions are crucial for the current
long-time-running Pi computation but it is still not perfect (coverage as about 90%)
○ Sometimes silent hardware errors may be not undetected, or uncorrected

41. My impression after reading
41
● This work just uses “y-cruncher” as a conventional software with conventional
methods, so that there is less novelty in term of the HPC field
● On the other hands, in term of the reliability of the long-time-running mathematical
calculation (or SRE challenge; Site Reliability Engineering), it’s a good tech report
● As a ads of Google Cloud and Pi day celebration: a great contribution
● It is a good thing to extend the Pi digits (“Pi digit is a measurement of civilization”)

42. Supplementals:
42

43. Let’s calc the Pi digits!
43
Docker image for testing “y-cruncher”
https://github.com/metaVariable/docker-y-cruncher
# clone
git clone https://github.com/metaVariable/docker-y-cruncher.git
# build
docker build . -t y-cruncher:v0.7.7.9500
# run
docker run -it y-cruncher:v0.7.7.9500 ./y-cruncher custom pi -dec:10000

44. Scalability
“As of v0.7.1, y-cruncher is coarse-grained paralleled. On shared and uniform memory, the
isoefficiency function is estimated to be Θ(p2). This means that every time you double the #
of processors, the computation size would need to be 4x larger to achieve the same
parallel efficiency.”
“The Θ(p2) heuristically comes from a non-recursive Bailey's 4-step FFT algorithm using a
sqrt(N) reduction factor. In both of the FFT stages, there are only sqrt(N) independent FFTs.
Therefore, the parallelism cannot exceed sqrt(N) for a computation of size N.”
44

45. Non-Uniform Memory
“As of 2018, y-cruncher is still a shared memory program and is not optimized for
non-uniform memory (NUMA) systems. So historically, y-cruncher's performance and
scalability has always been very poor on NUMA systems. While the scaling is still ok on
dual-socket systems, it all goes downhill once you put y-cruncher on anything that is
extremely heavily NUMA. (such as quad-socket Opteron systems)”
“While y-cruncher is not "NUMA optimized", it has been "NUMA aware" since v0.7.3 with
the addition of node-interleaving memory allocators.”
45