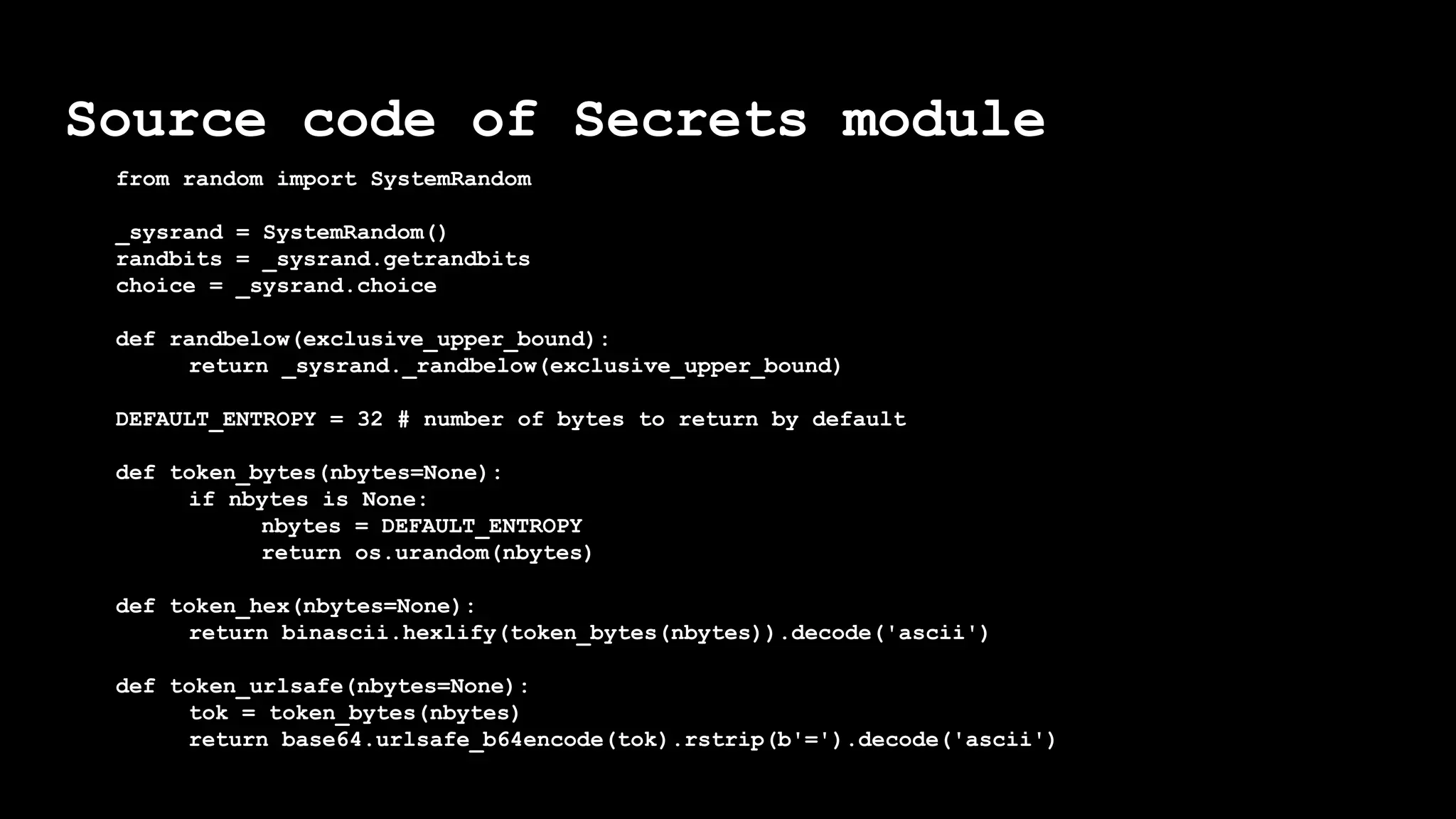
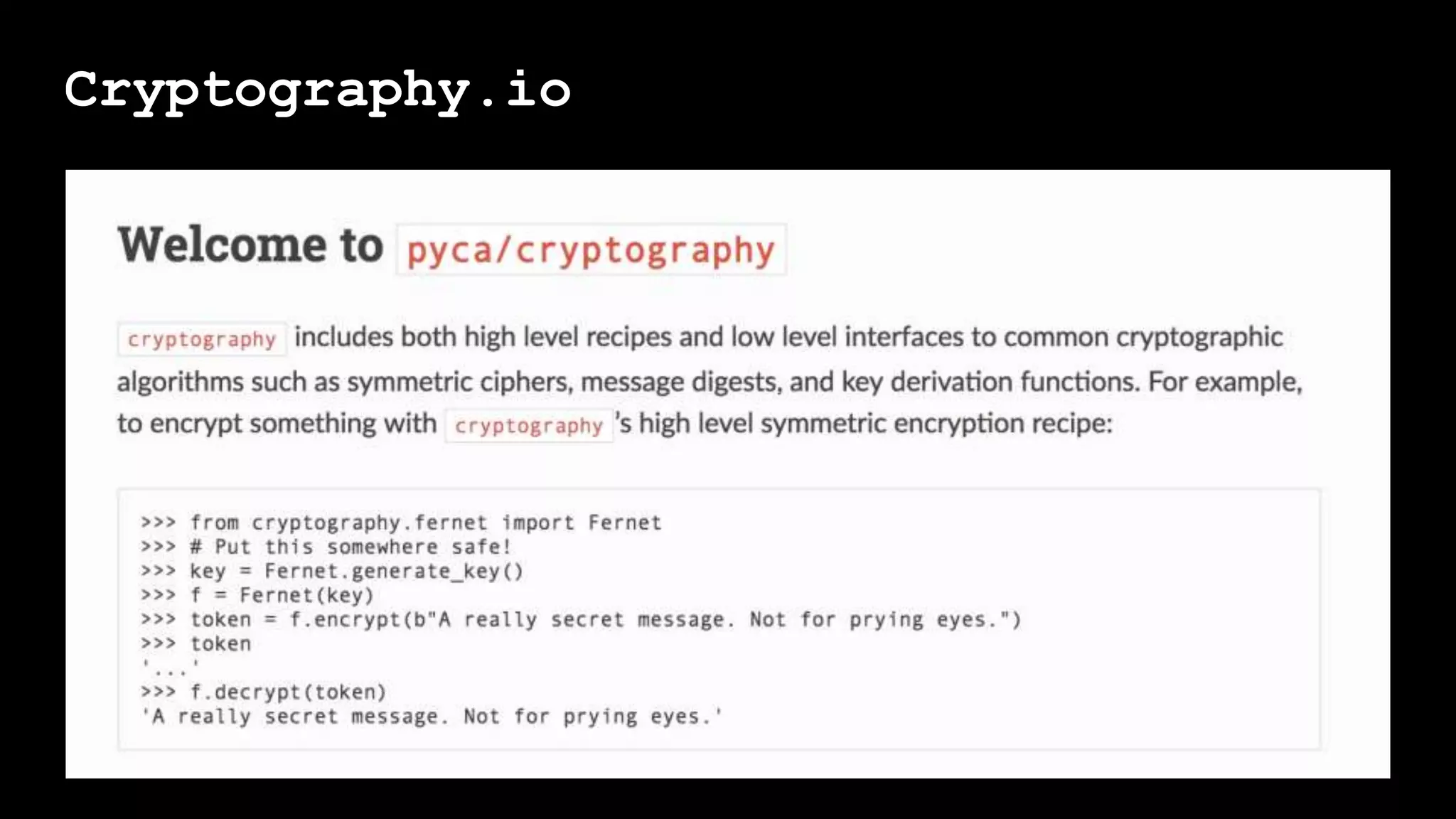
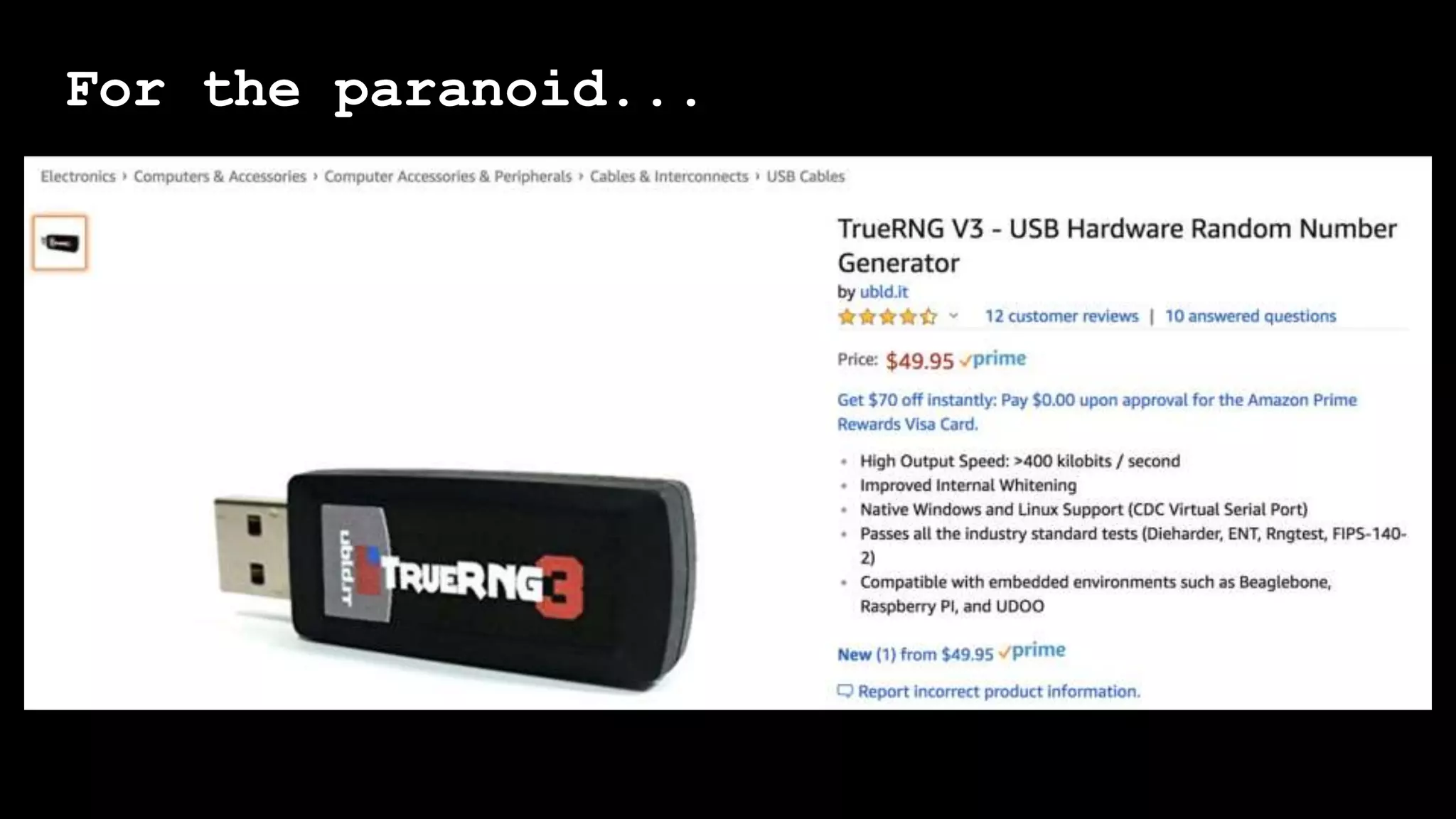
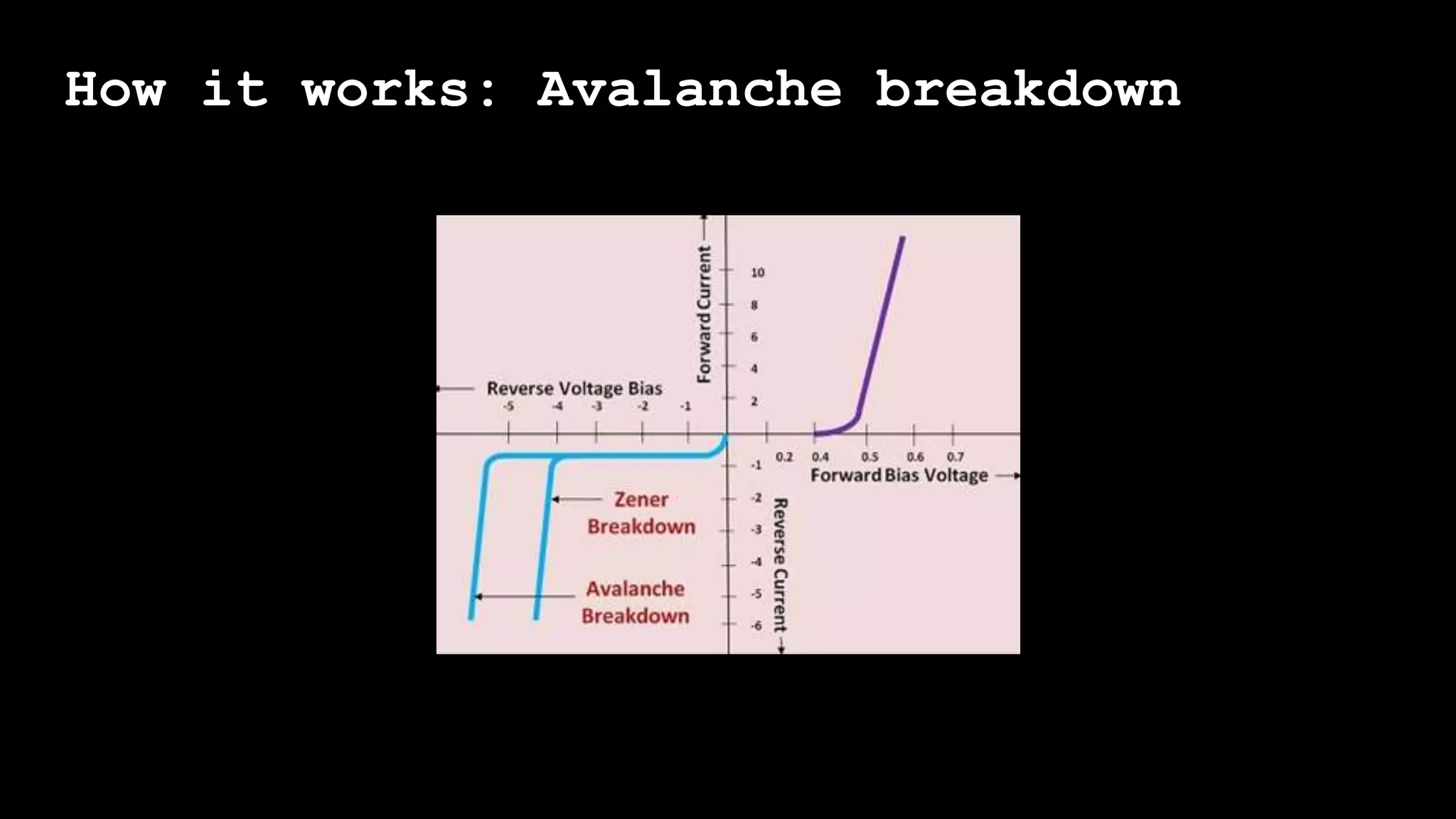
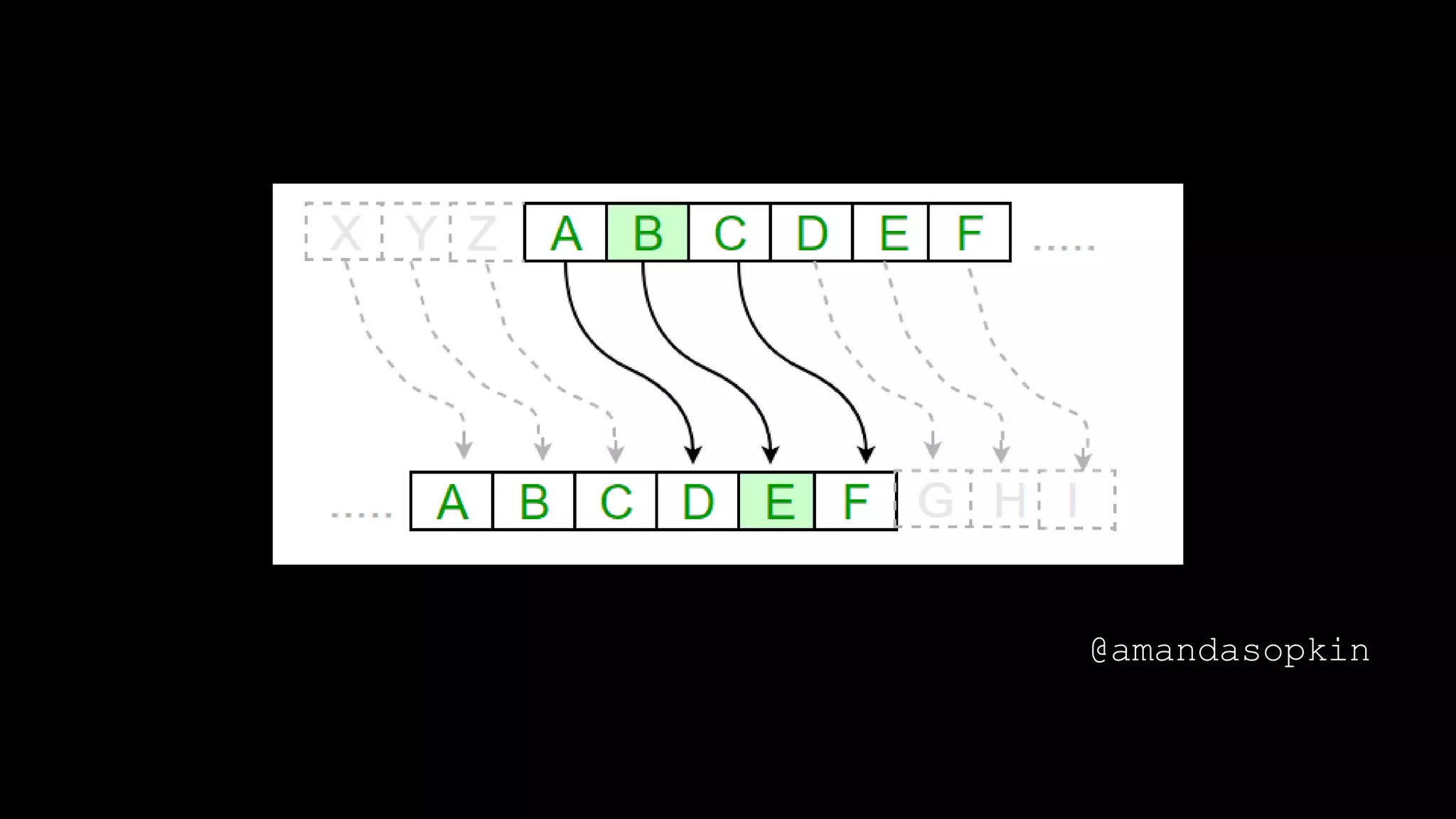
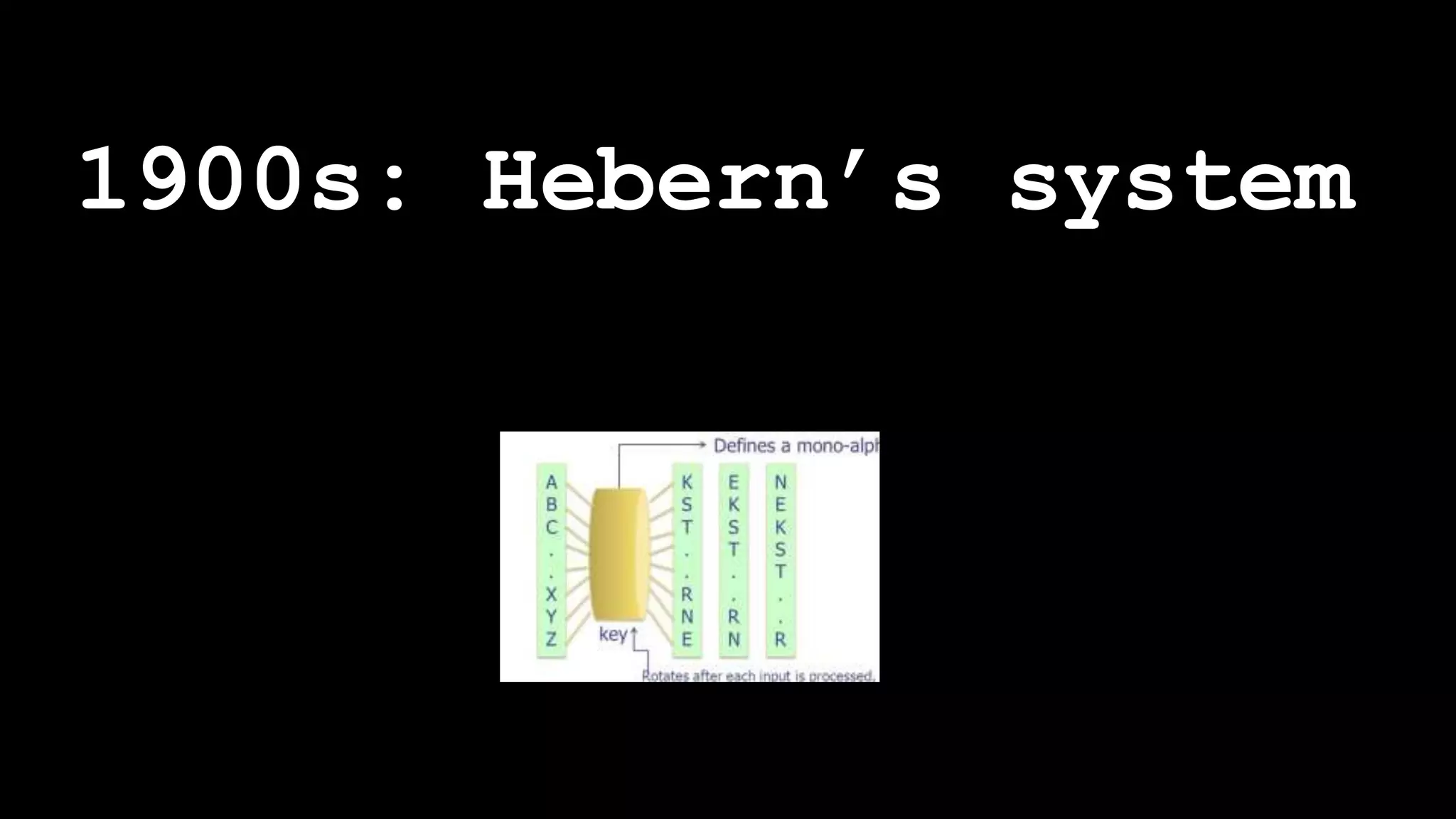
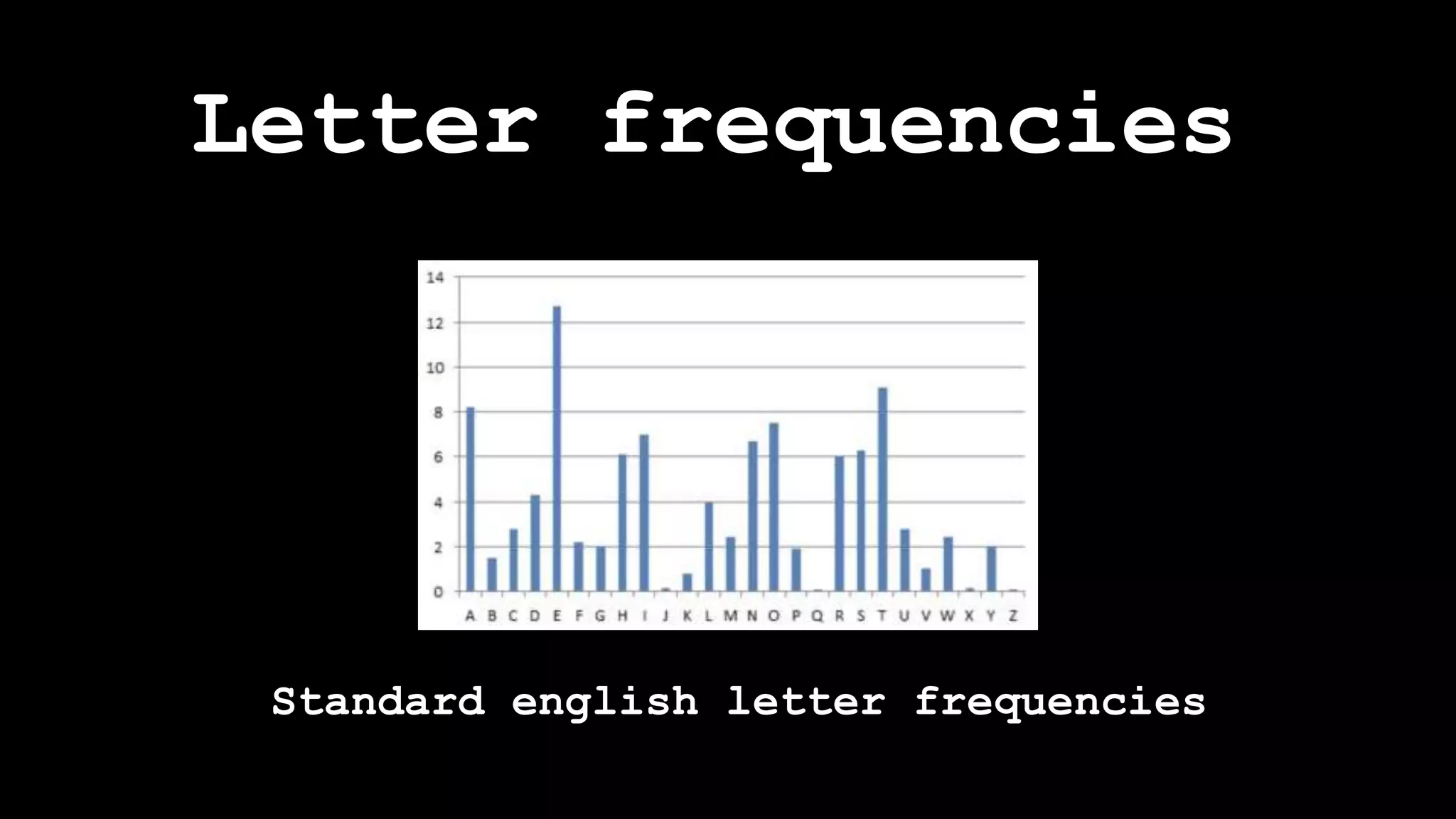
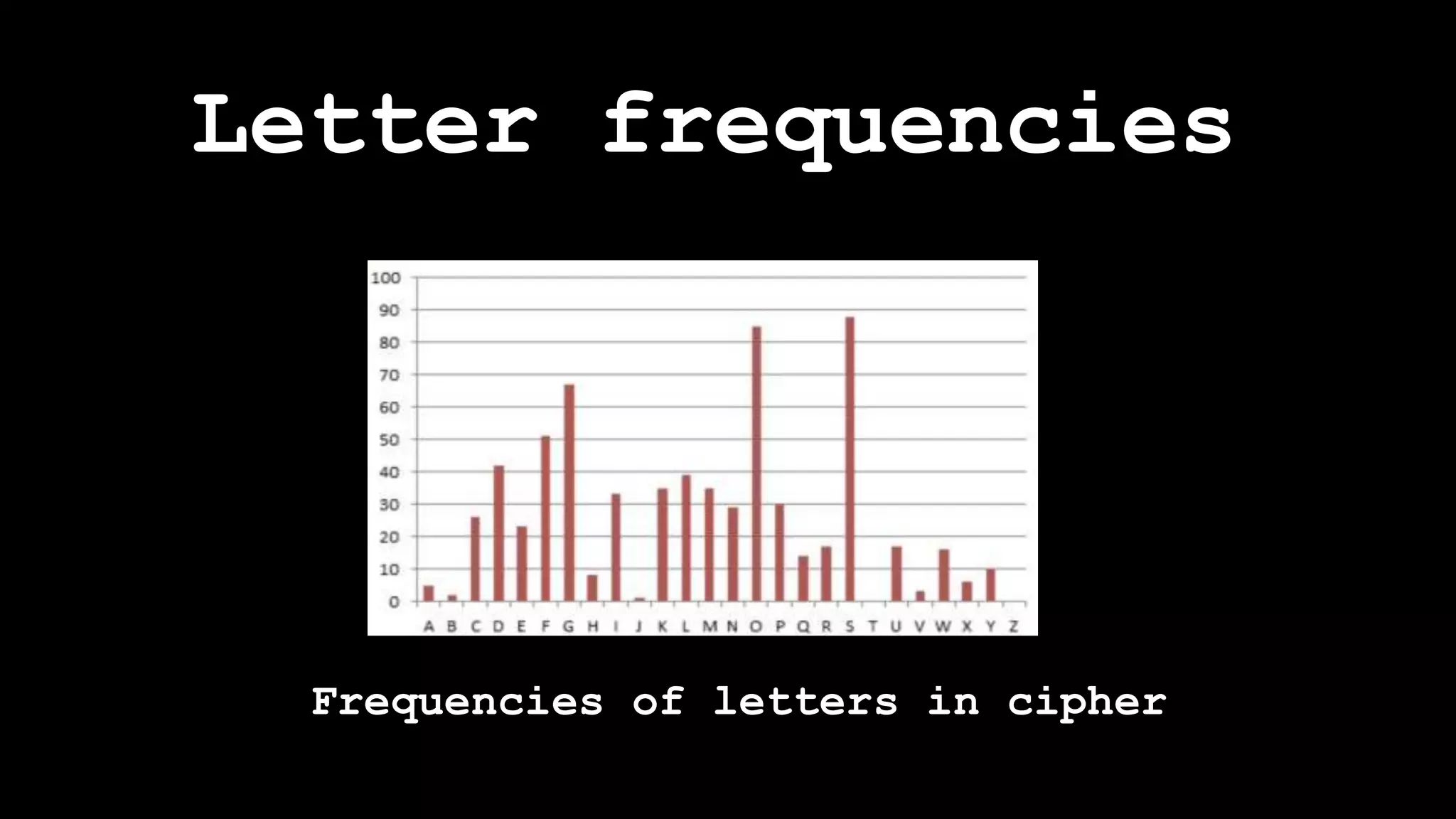
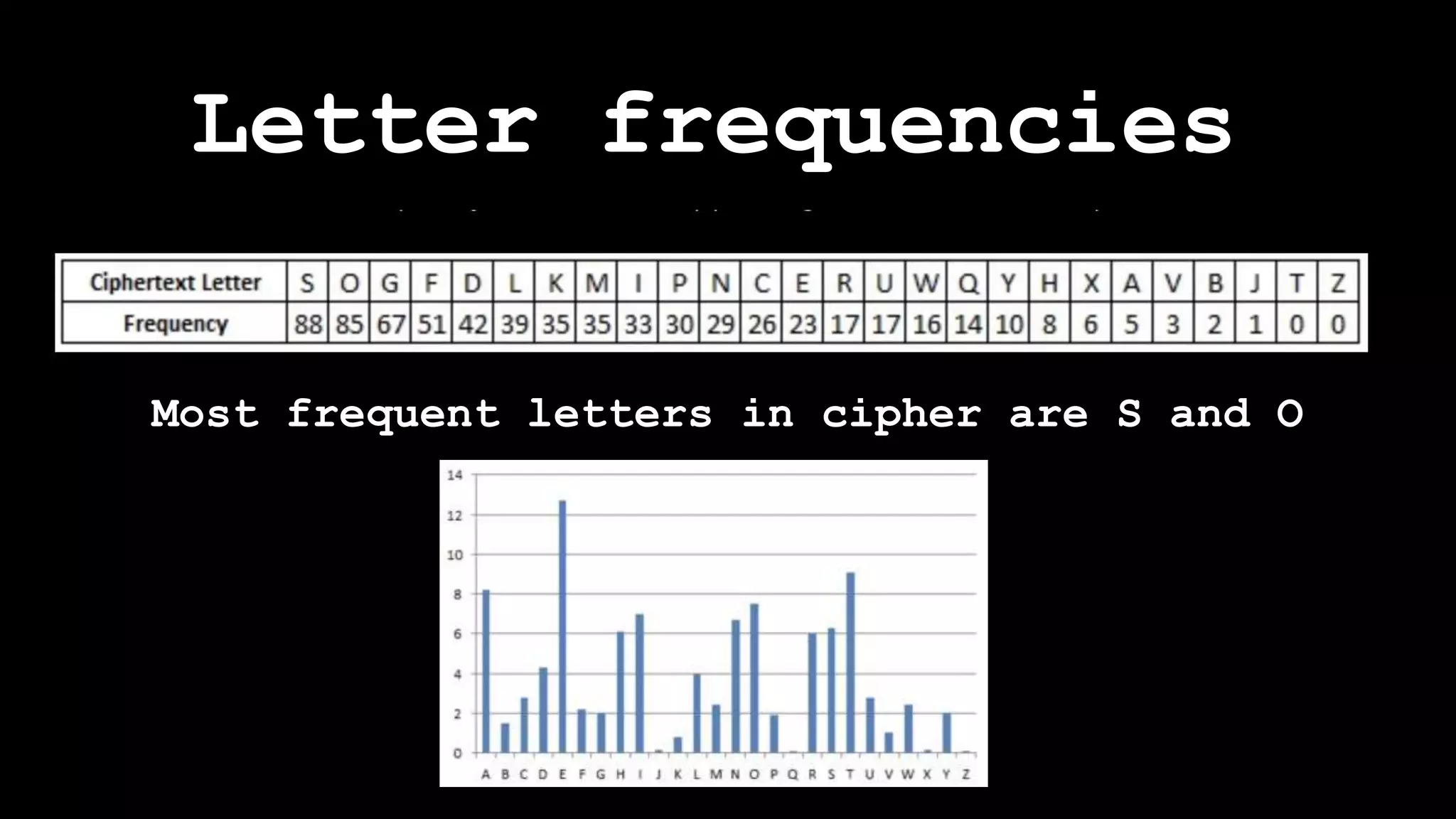
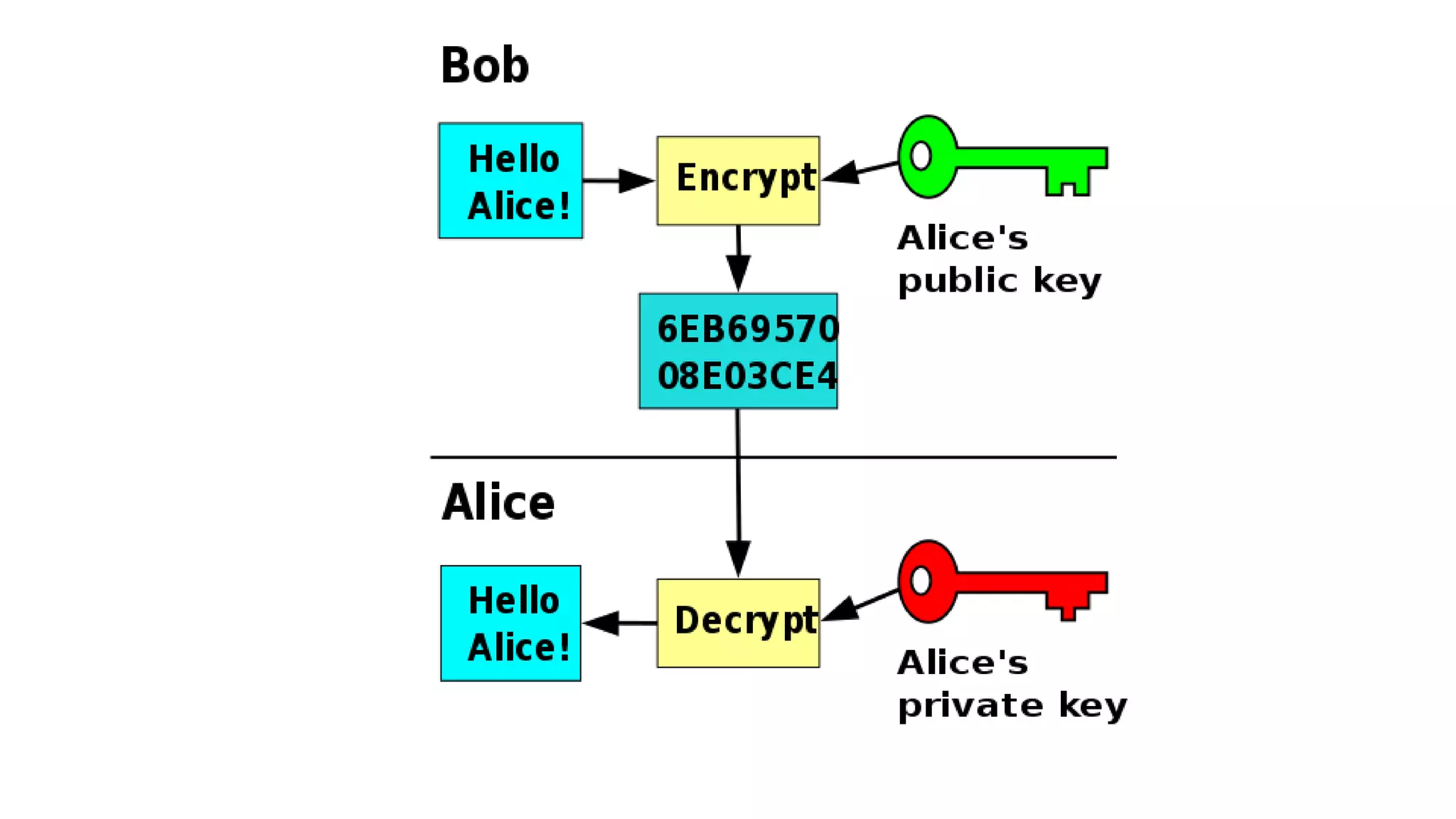
The document outlines the importance of randomness in cryptography and its historical evolution, detailing various cryptographic systems from ancient hieroglyphics to modern algorithms like AES and RSA. It highlights the challenges involved in achieving true randomness, including issues with existing random number generators and the controversial dual-EC-DRBG algorithm, which had known vulnerabilities. The presentation also introduces Python's 'secrets' module as a better option for cryptographic applications and emphasizes the mathematical and computational significance of randomness for secure communications.













































































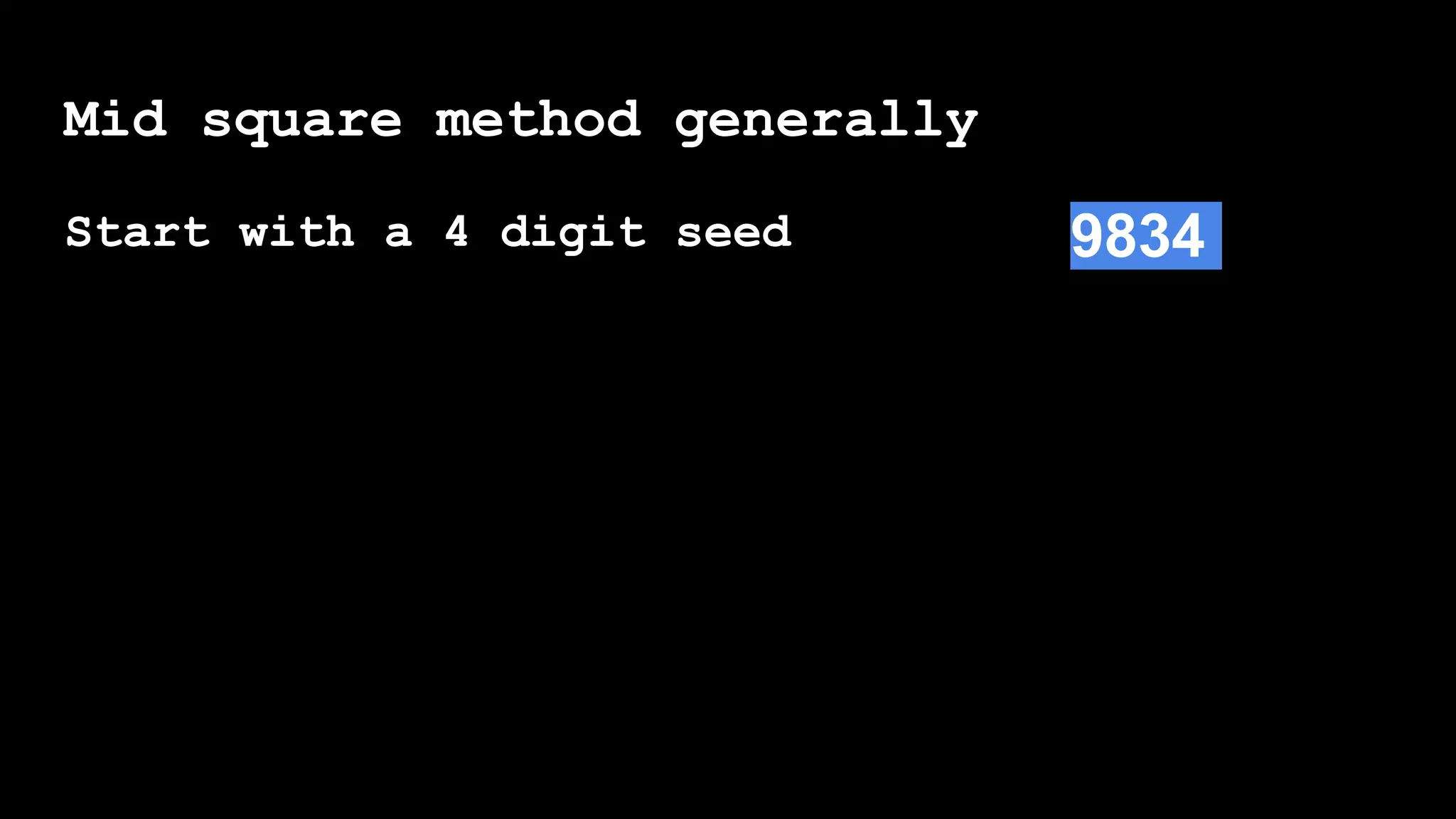
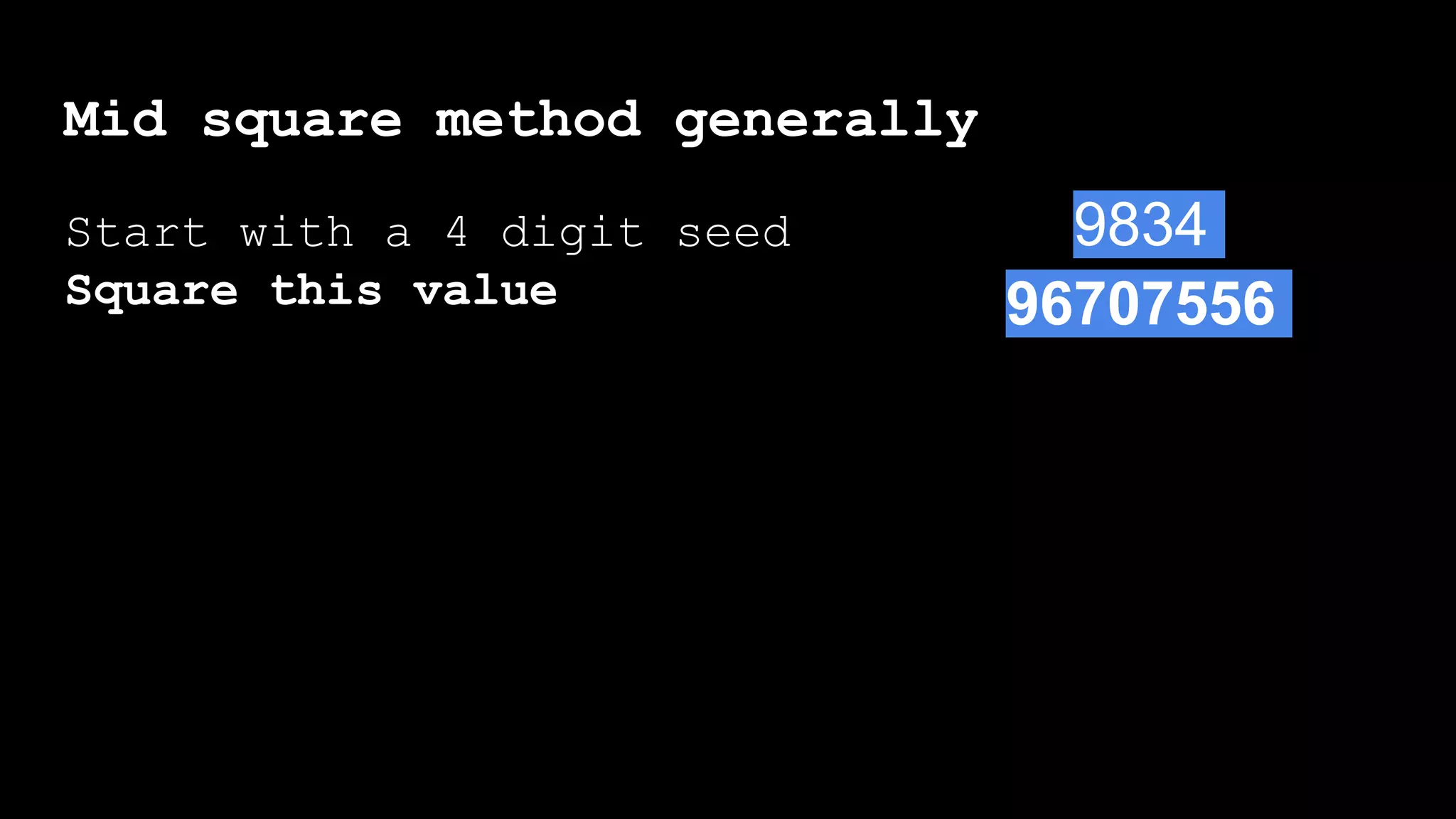



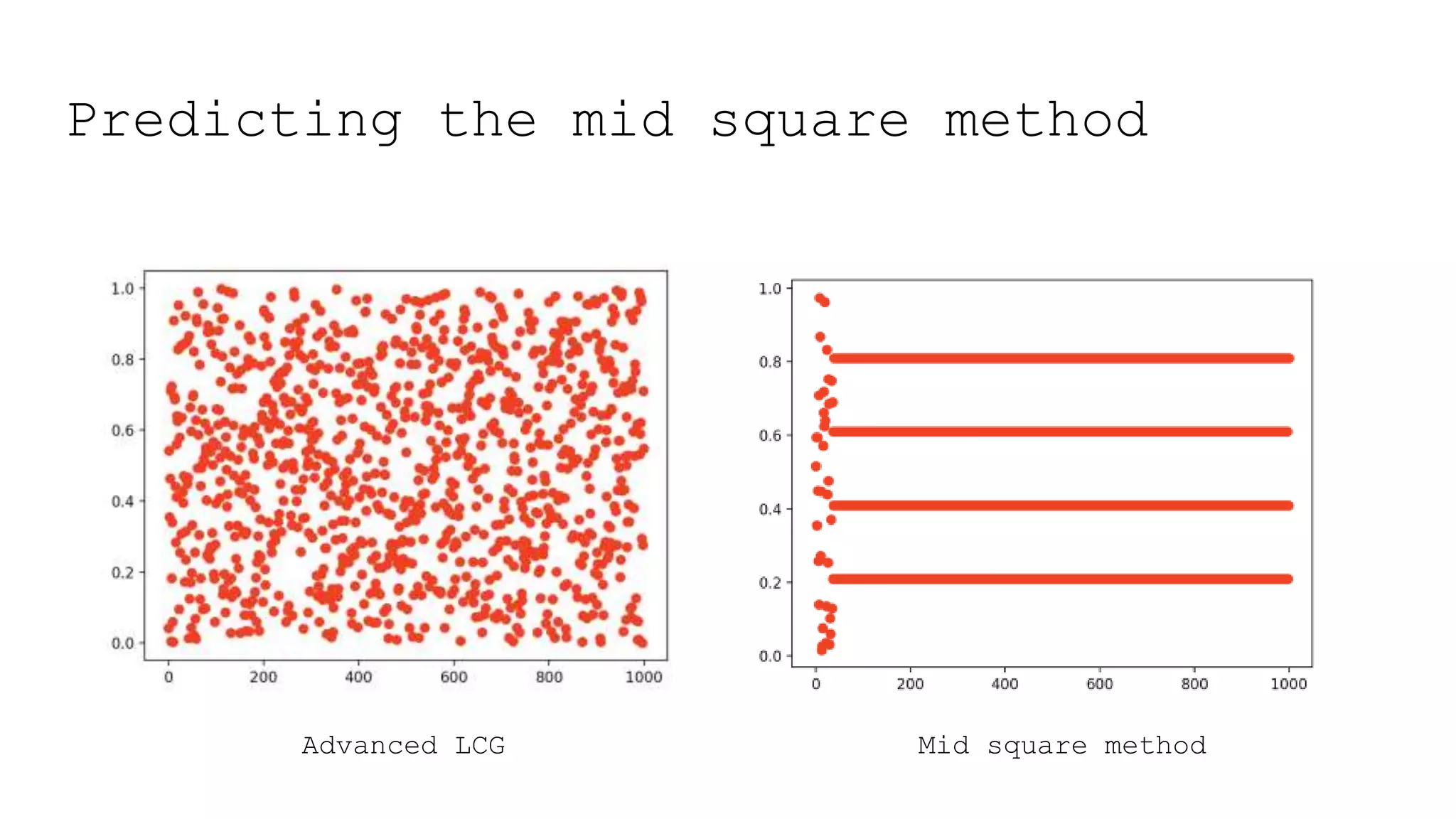
![Mid square method
seed_number = int(input("Please enter a four digit number:n[####] "))
number = seed_number
already_seen = set()
counter = 0
while number not in already_seen:
counter += 1
already_seen.add(number)
number = int(str(number * number).zfill(8)[2:6])
print(f"#{counter}: {number}")
print(f"We began with the seed {seed_number}, and"
f" we repeated ourselves after {counter} steps"
f" with {number}.")](https://image.slidesharecdn.com/1-amandasopkin-190127100417/75/Amanda-Sopkin-Computational-Randomness-Creating-Chaos-in-an-Ordered-Machine-Codemotion-Milan-2018-97-2048.jpg)
![Mid square method
Please enter a four digit number: [####]
5859
#1: 3278
#2: 7452
#3: 5323
#4: 3343
#5: 1756
#6: 835
#7: 6972
#8: 6087
#9: 515
#10: 2652
.......
#59: 24 #60: 5 #61: 0 #62: 0 We began with the seed 5859, and we repeated ourselves after 62 steps
with 0.](https://image.slidesharecdn.com/1-amandasopkin-190127100417/75/Amanda-Sopkin-Computational-Randomness-Creating-Chaos-in-an-Ordered-Machine-Codemotion-Milan-2018-98-2048.jpg)



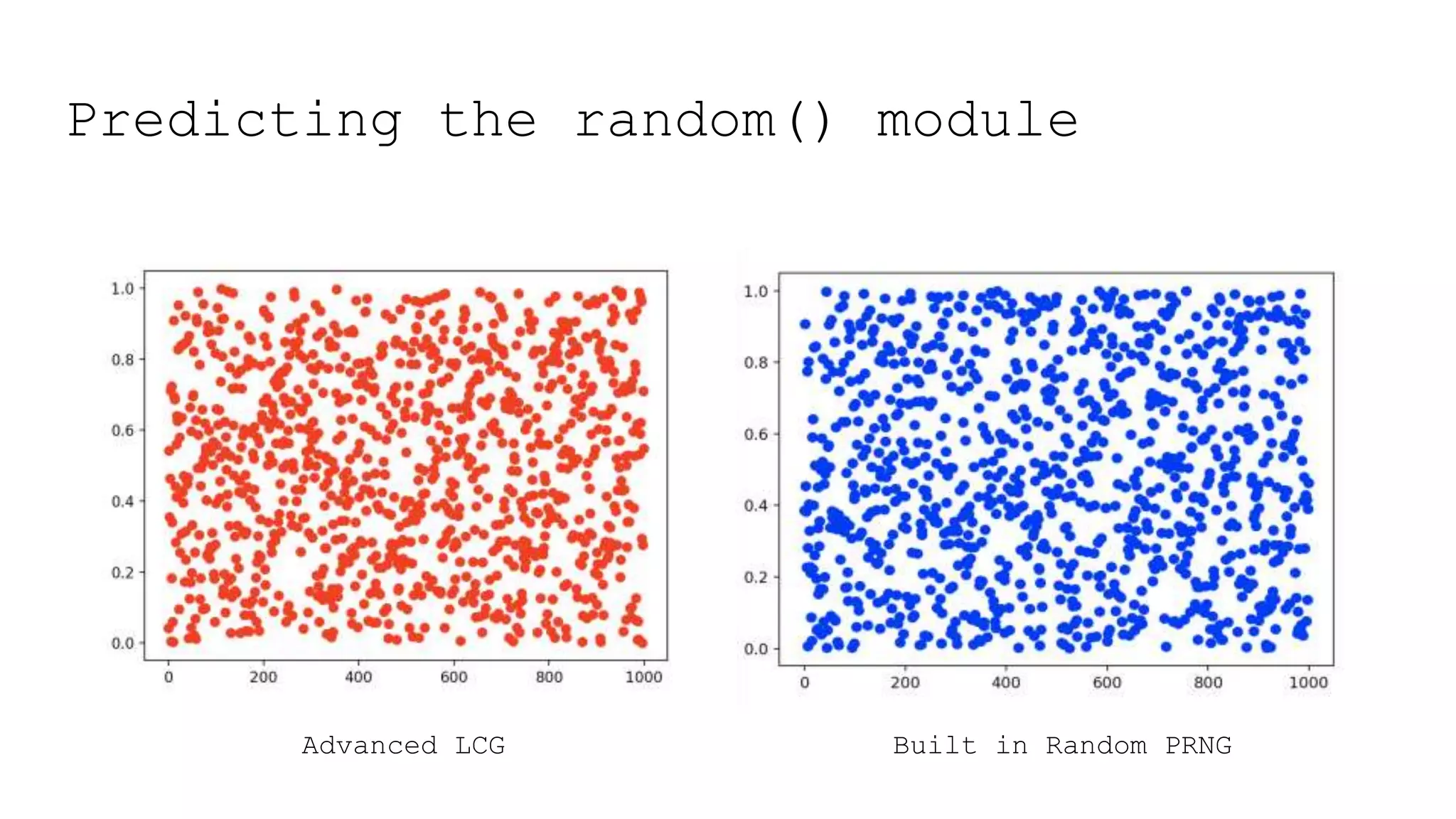
![Predicting the random() module
from random import random
import matplotlib.pyplot as plt
def uni(n, m, a, c, seed):
sequence = []
Xn = seed
for i in range(n):
Xn = ((a*Xn + c) % m)
sequence.append(Xn/float(m-1))
return(sequence)
x = range(1000)
y_1 = uni(1000, 2**32, 11695477, 1, datetime.now().microsecond)
y_2 = [random() for i in range(1000)]
plt.plot(x, y_1, "o", color="blue")
plt.show()
plt.plot(x, y_2, "o", color="red")
plt.show()](https://image.slidesharecdn.com/1-amandasopkin-190127100417/75/Amanda-Sopkin-Computational-Randomness-Creating-Chaos-in-an-Ordered-Machine-Codemotion-Milan-2018-103-2048.jpg)