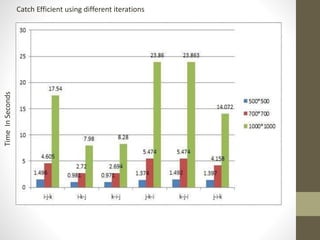
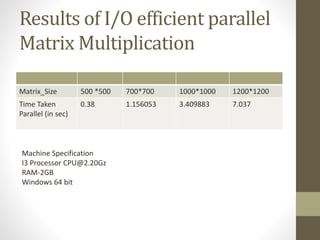
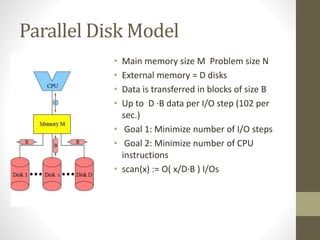
This document presents an overview of making matrix multiplication algorithms more I/O efficient. It discusses the parallel disk model and how to incorporate locality into algorithms to minimize I/O steps. Cannon's algorithm for matrix multiplication in a 2D mesh network is described. Loop interchange is discussed as a way to improve cache efficiency when multiplying matrices by exploring different loop orderings. Results are shown for parallel I/O efficient matrix multiplication on different sized matrices, with times ranging from 0.38 to 7 seconds. References on cache-oblivious algorithms and distributed memory matrix multiplication are provided.

1. I/O Efficient Matrix
Multiplication
Presented By
Shubham Joshi (2011227)
Shubham Jaju (2011226)

2. Contents
• I/O efficient
- Parallel Disk Model
- how to make algorithm i/o efficient
• Matrix Multiplication in 2D mesh
- Cannon’s Algorithm
• I/O efficient matrix multiplication (MPI model)
• Results & Conclusion
• References

3. Parallel Disk Model
• Main memory size M Problem size N
• External memory = D disks
• Data is transferred in blocks of size B
• Up to D ·B data per I/O step (102 per
sec.)
• Goal 1: Minimize number of I/O steps
• Goal 2: Minimize number of CPU
instructions
• scan(x) := O( x/D·B ) I/Os

4. How to make algorithms I/O-
efficient?
Only a few golden rules:
• Avoid unstructured access patterns.(e.g. avoid goto
statement)
• Incorporate LOCALITY directly into the algorithm.
Tools:
• Scanning: scan(N) = O(N/DB) I/Os.
• Special I/O-efficient data structures (BTrees , B+ Trees).
• “Simulation” of parallel algorithms.

5. i/o efficient matrix
multiplication
Principle of locality takes two forms:
Temporal Locality: says that if any memory location is accessed
now, it is more likely to be accessed again in near future.
Spatial Locality: says that if any memory location is accessed
now, then it's neighboring memory locations are expected to
be accessed in near future.
Let's see how can we make use of the cache properties to
speed up our Matrix Multiplication program.

6. Assume that the 2-D array matrix is stored in a row-major order
a[0][0],a[0][1],...,a[0][n−1],a[1][0]
,a[1][1],...,a[1][n−1]...a[n−1][n−1]
The accesses into array C are
made in the following order:
• C[0][0] is accessed n times – For the first execution of k loop.
• C[0][1] is accessed n times – For the second execution of k loop.
• C[0][2] is accessed n times – For the third execution of k loop.
• ...
• C[1][0] is accessed n times – For the (n+1)th execution of k loop.
Since the same element is accessed repeatedly and accesses are
made sequentially, both temporal and spatial locality of reference is
observed.
For C, accesses are already optimized for cache!

7. • The accesses into array A are made in the following order:
• A[0][0],A[0][1],A[0][2],...,A[0][n] – This whole
sequence n times, for each iteration of k loop under a single
iteration of j loop.
• A[1][0],A[1][1],A[1][2],...,A[1][n] – This whole
sequence n times, for each iteration of k loop under a single
iteration of j loop.
• ...
• ...
• A[n][0],A[n][1],A[n][2],...,A[n][n] – This whole
sequence n times, for each iteration of k loop under a single
iteration of j loop.
Hence, each row of array A is accessed n times and each
element in the row is accessed sequentially. We observe good
spatial locality of reference. But the same element is not
referenced repeatedly so no temporal locality.

8. • The accesses into array B are made in the following order:
• B[0][0],B[1][0],B[2][0],...,B[n][0]
• B[0][1],B[1][1],B[2][1],...,B[n][1]
• ...
• B[0][n],B[1][n],B[2][n],...,B[n][n]
• Then again,
• B[0][0],B[1][0],B[2][0],...,B[n][0]
• B[0][1],B[1][1],B[2][1],...,B[n][1]
• ...
• B[0][n],B[1][n],B[2][n],...,B[n][n]
The whole array is accessed once and only then repetition
starts. So there's no spatial locality or temporal locality for B.
Each element will incur a cache miss on every access made to it.
And thus we have a cache miss on every execution of the
multiplication statement

9. Improving cache efficiency
To improve upon this traditional i−j−k setting,
we can employ loop interchange.
By trying out the other 5 combinations of the loop orderings
namely, i−k−j, j−k−i ,j−i−k, k−i−j and k−j−i we find that i−k−j is the
optimal

10. • C[0][0],C[0][1],C[0][2],...,C[0][n] – This whole sequence n times, for
each iteration of k loop……
• C[n][0],C[n][1],C[n][2],...,C[n][n] – This whole sequence n times, for
each iteration of k loop.
Now C has good spatial locality.
Similarly,
A enjoys good temporal as well as spatial locality.
B now has spatial locality.

11. Catch Efficient using different iterationsTimeInSeconds

12. Matrix Multiplication in 2D mesh
Mesh Network:
A set of nodes arranged in the form of a p dimensional lattice is called a mesh network.
In a mesh network only neighbouring nodes can communicate with each other.
Cannon’s Algorithm
Procedure MATRIXMULT
begin
for k = 1 to n-1 step 1 do
begin
for all Pi,j where i and j ranges from 1 to n do
if i is greater than k then
rotate a in the east direction
end if
if j is greater than k then
rotate b in the south direction
end if
end
for all Pi;j where i and j lies between 1 and n do
compute the product of a and b and store it in c
for k= 1 to n-1 step 1 do for all Pi;j where i and j ranges from 1 to n do
rotate a in the east
rotate b in the south
c=c+aXb
end

13. Results of I/O efficient parallel
Matrix Multiplication
Matrix_Size 500 *500 700*700 1000*1000 1200*1200
Time Taken
Parallel (in sec)
0.38 1.156053 3.409883 7.037
Machine Specification
I3 Processor CPU@2.20Gz
RAM-2GB
Windows 64 bit

14. References
Cache-Oblivious Algorithms – Harald Prokop
MIT June 1999
Matrix Multiplication on a Distributed Memory Machine,
www.phy.ornl.gov

15. Thank You