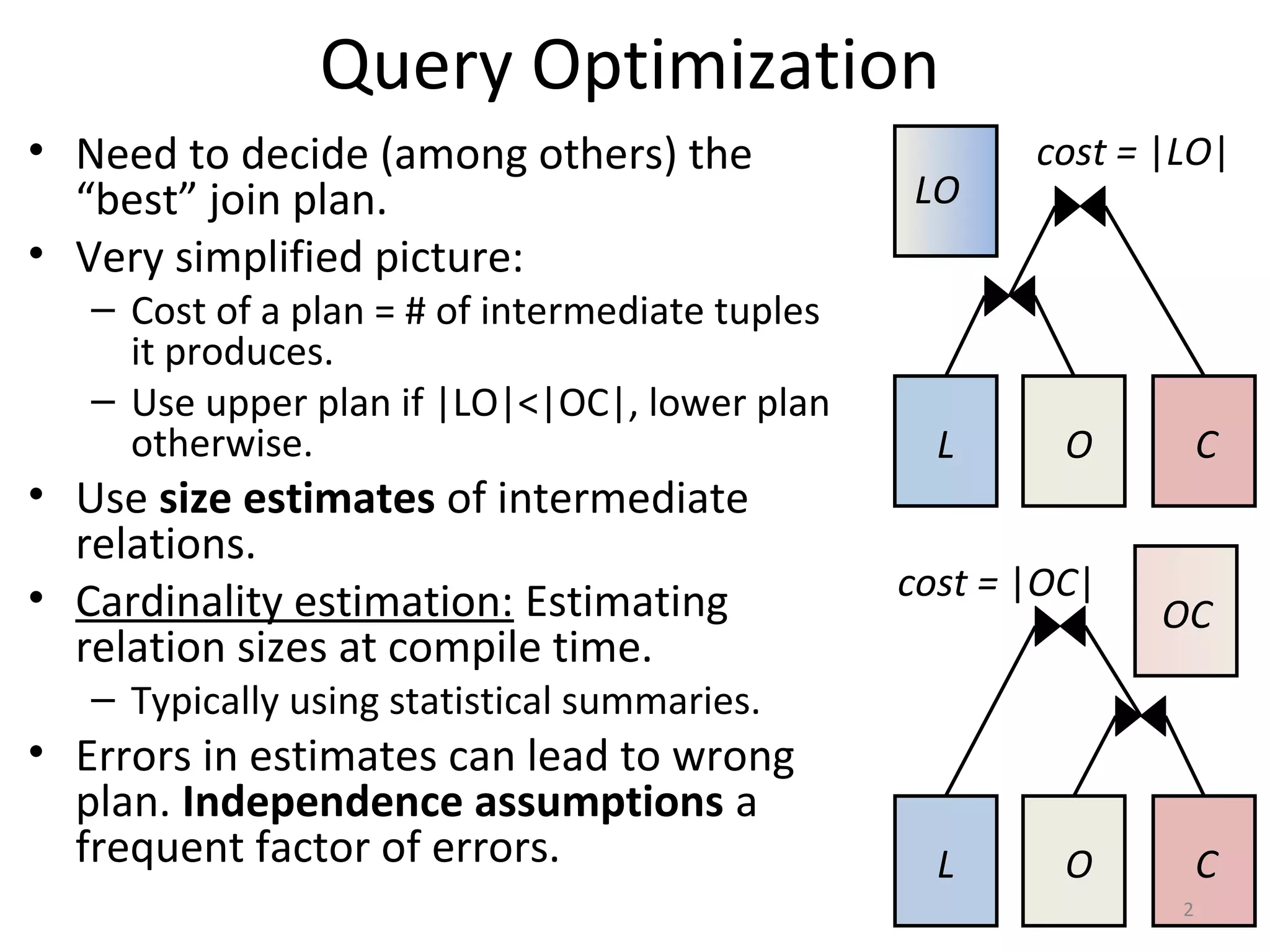
The document presents a technique for selectivity estimation in query optimization without assuming independence between attributes. It uses lightweight graphical models, specifically a junction tree, to capture correlations and approximate the joint probability distribution over relevant variables. This avoids the independence assumptions made by traditional optimizers that can lead to errors in cardinality estimates and suboptimal query plans. The graphical models are implemented within PostgreSQL to provide selectivity estimates with an order of magnitude better accuracy compared to the default PostgreSQL estimates, while keeping optimization time low.

1. Lightweight Graphical Models for
Selectivity Estimation without
Independence Assumptions
Kostas Tzoumas
Amol Deshpande
Christian S. Jensen

2. Query Optimization
• Need to decide (among others) the
“best” join plan.
• Very simplified picture:
– Cost of a plan = # of intermediate tuples
it produces.
– Use upper plan if |LO|<|OC|, lower plan
otherwise.
• Use size estimates of intermediate
relations.
• Cardinality estimation: Estimating
relation sizes at compile time.
– Typically using statistical summaries.
• Errors in estimates can lead to wrong
plan. Independence assumptions a
frequent factor of errors.
L O C
LO
cost = |LO|
L O C
OC
cost = |OC|
2

3. Cardinality Estimation
• Original system R optimizer assumes
– Uniform distribution of attributes
• Addressed by attribute-level synopsis (e.g., 1D
histogram and wavelets) accurate estimation of single➔
attributes.
– Independence among
• Attribute values of a table
– Addressed by table-level synopsis (multi-D histograms) to
estimate the joint probability distributions of two or many
variables.
• Join predicates between different tables
– Addressed by schema-level synopsis to capture the joint
probability distribution of attributes and join indicators.

4. Independence Assumption
|L’| = Pr(eprice in [e1,e2]) |L|
|O’| = Pr(tprice in [t1,t2]) |O|
|L’O’| = Pr(l_orderkey=o_orderkey)|L’||O’|
|L’O’| = Pr(l_orderkey=o_orderkey)
Pr(eprice in [e1,e2])
Pr(tprice in [t1,t2]) |L||O|
•Results to under-estimation of |L’O’| 
wrong query plan, nested loop join.
•Can result in orders of magnitude slower
execution.
•Solution: estimate joint probabilities: |L’O’|
= Pr (l_orderkey=o_orderkey,
eprice in [e1,e2],
tprice in [t1,t2]) |L||O|
L O C
HJ
NLJ
σL σΟ σC
L’ O’ C’
L’O’
4
select c_name,c_address
from lineitem,orders,customer
where l_orderkey=o_orderkey and
o_custkey=c_custkey and
o_totalprice in [t1,t2] and
l_extendedprice in [e1,e2]
and c_acctbal in [b1,b2]

5. Problem Setting
• Database + workload  schema graph
• Schema graph  Set of random variables (descriptive
attributes and join indicators)
• Goal: Approximate P(JLO, JLP, JLS, JSC, JOC, L.sdate, L.cdate,
L.rdate, O.odate, P.size, S.acctbal,C.acctbal)
sdate
cdate
rdate
lineitem
odate
orders
size
part
acctbal
supplier
acctbal
customer
JLO ≡
L.okey=O.okey
JOC ≡
O.ckey=C.ckey
JLS ≡
L.skey=S.skey
JLP ≡
L.pkey=P.pkey
JSC ≡
S.nkey=C.nkey
Join indicator
A binary random variable
Captures the “event” that
two random tuples join.
We don’t need “key”
attributes in the model
(hard to approximate).
Pr(JOC=T)=sel(O.ckey=C.ckey)
Problem:
Exponential blow-
up of storage space
and selectivity
estimation time.
5

6. Graphical Models
• Exploit independence and conditional independence
to factor the full joint distribution.
– X┴Y ↔P(X,Y)=P(X)P(Y)
– X┴Z|Y ↔ P(X,Y,Z)=P(X,Y)P(Y,Z)/P(Y)
• Bayesian networks
– Graphical representation of a set of cond. inds
– Express a factorization of the joint distribution
• Selectivity estimation is solving inference problem
(computing marginal distributions of the form of P(Xi|
Xj=xj)).
– High dimensional distributions  high overhead
– Construction algorithms do not scale.
X Y Z
6

7. Fixed Structure
• “Tailored” solution
– only 2D histograms to ensure scalable construction
• Relational independencies:
– L.rdate ┴ O.odate
σL.rdate=a,O.odate=b(LxO)=σL.rdate=a(L) x σO.odate=b(O)
– L.rdate ┴ JSC
– JLO ┴ JSC
• Model Design decisions
– Join indicator has at most two parents; one from
each relation
– BN within a relation as a directed tree 7

8. Bayesian Network
sdate
cdaterdate
size S.acctbal S.acctbal
odate
JLP JLS
JSC
JOC
JLO
lineitem
part supplier customer
orders
8

9. Moral Graph
sdate
cdaterdate
size S.acctbal C.acctbal
odate
JLP JLS
JSC
JOC
JLO
9

10. Chordal Graph
sdate
cdaterdate
size S.acctbal C.acctbal
odate
JLP JLS
JSC
JOC
JLO
10

11. Junction Tree
sdate
rdate
C.acctbal
odate
sdate
C.acctbal
S.acctbal
sdate
sdate
cdate
odate
cdate
odate
JLO
sdate
S.acctbal
JLS
sdate
size
JLP
odate
C.acctbal
JOC
S.acctbal
C.acctbal
JSC
sdate
sdate
sdate
odate
sdate
sdate
cdate
odate
odateacctbal
Distributions to be kept =
marginals of “cliques” and
“separators.”
Factorization achieved!
Storage space:
•(sdate,rdate)  One 2D histogram
•(odate,acctbal,JOC)  Two 2D histograms (JOC=false,true)
•(acctbal,odate,sdate)  Three 1D histograms
Only 2D histograms needed! 11
Efficient selectivity estimation
via junction tree propagation.

12. Selectivity Estimation
sdate
rdate
C.acctbal
odate
sdate
C.acctbal
S.acctbal
sdate
sdate
cdate
odate
cdate
odate
JLO
sdate
S.acctbal
JLS
sdate
size
JLP
odate
C.acctbal
JOC
S.acctbal
C.acctbal
JSC
sdate
sdate
sdate
odate
sdate
sdate
cdate
odate
odateacctbal
Estimate size of query:
select c_name,c_address
from lineitem,orders,customer
where l_orderkey=o_orderkey and
o_custkey=c_custkey and
l_sdate<=“25/7/2011” and
c_acctbal<=200000
Equivalent: Estimate
Pr(JLO=true,
JOC=true,
sdate<=“25/7/2011”,
C.acctbal<=200000)
Extract “Steiner tree”:
Minimal subtree that
contains JLO, JOC, sdate,
C.acctbal 12

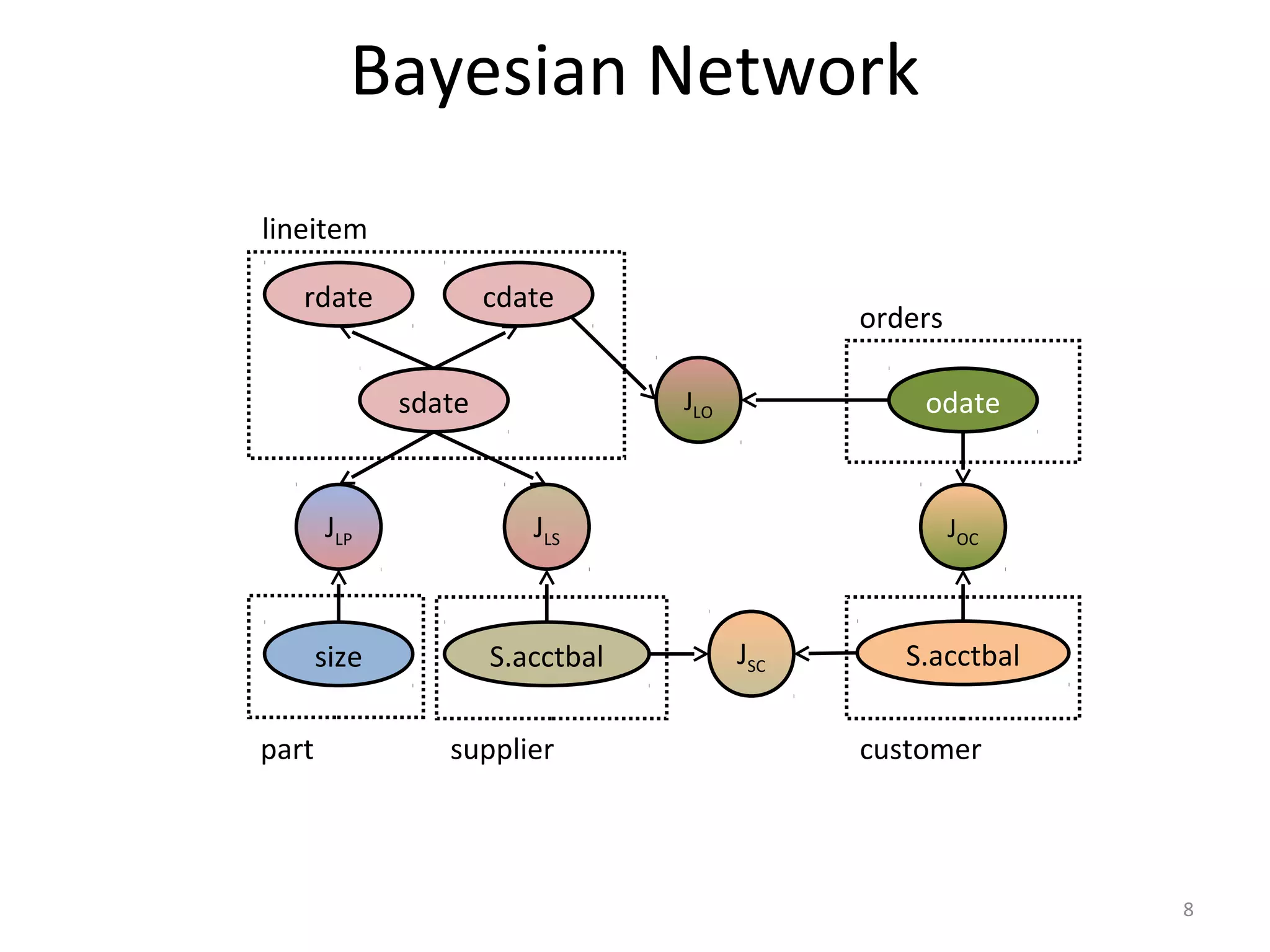
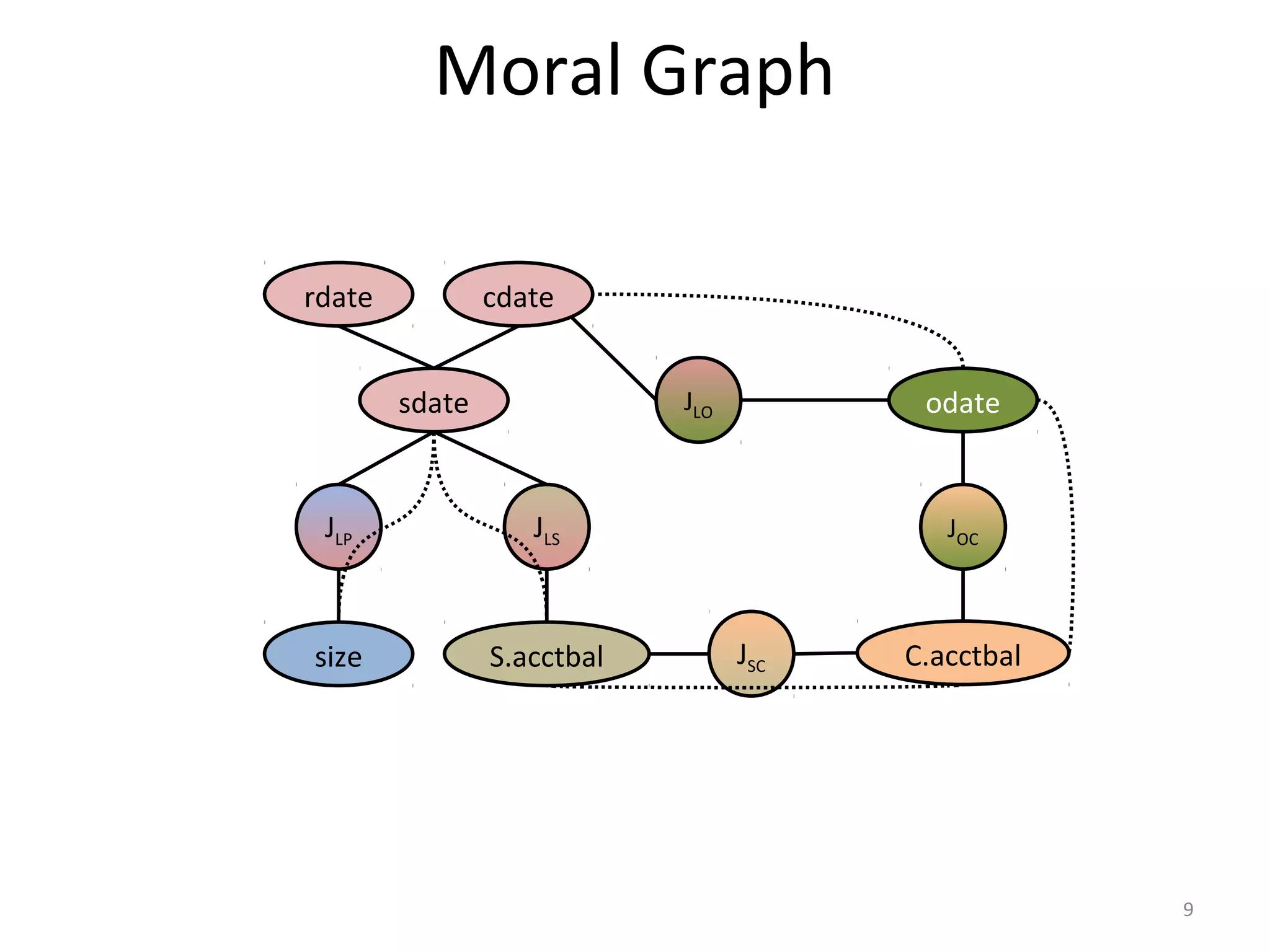
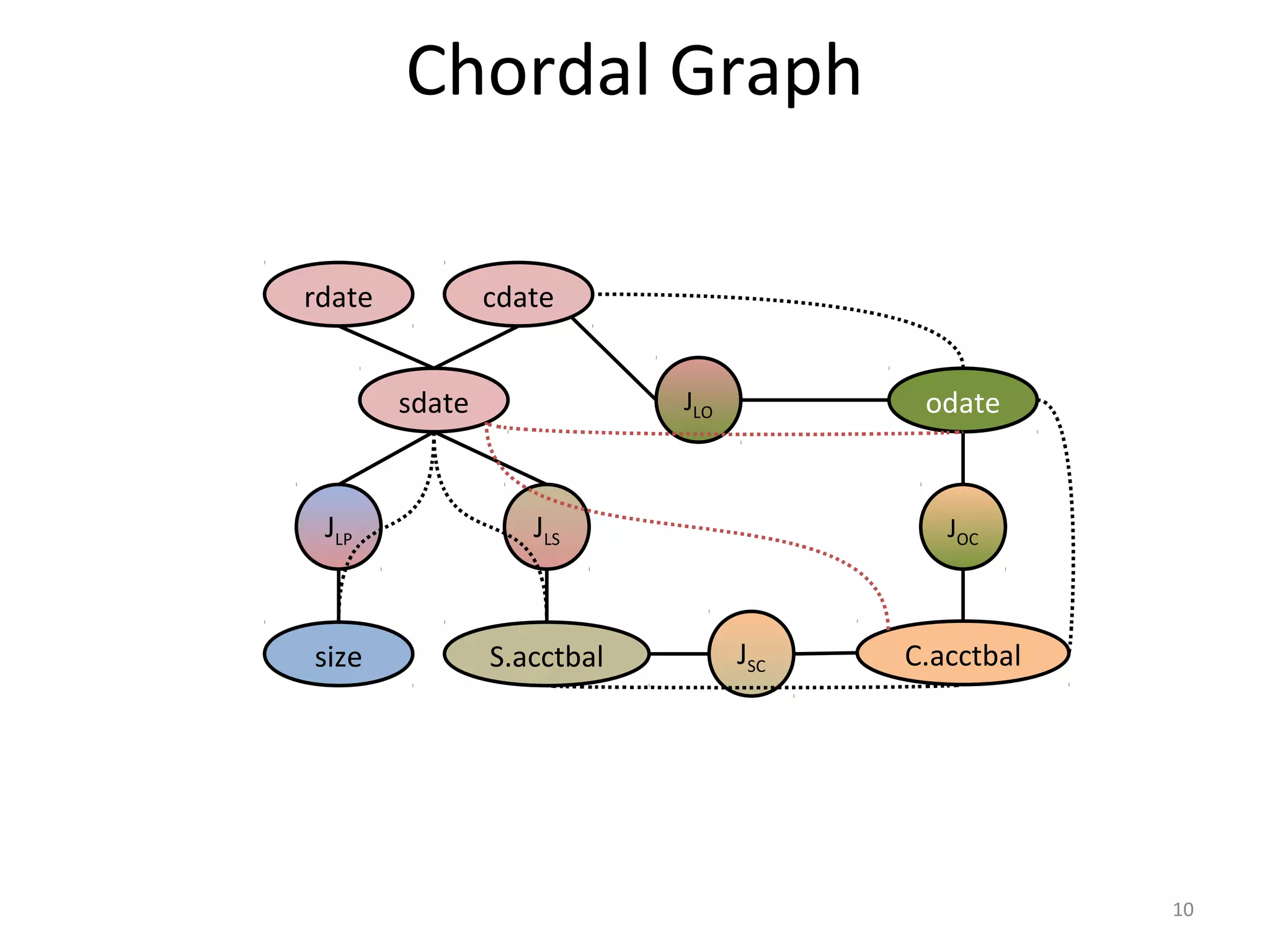
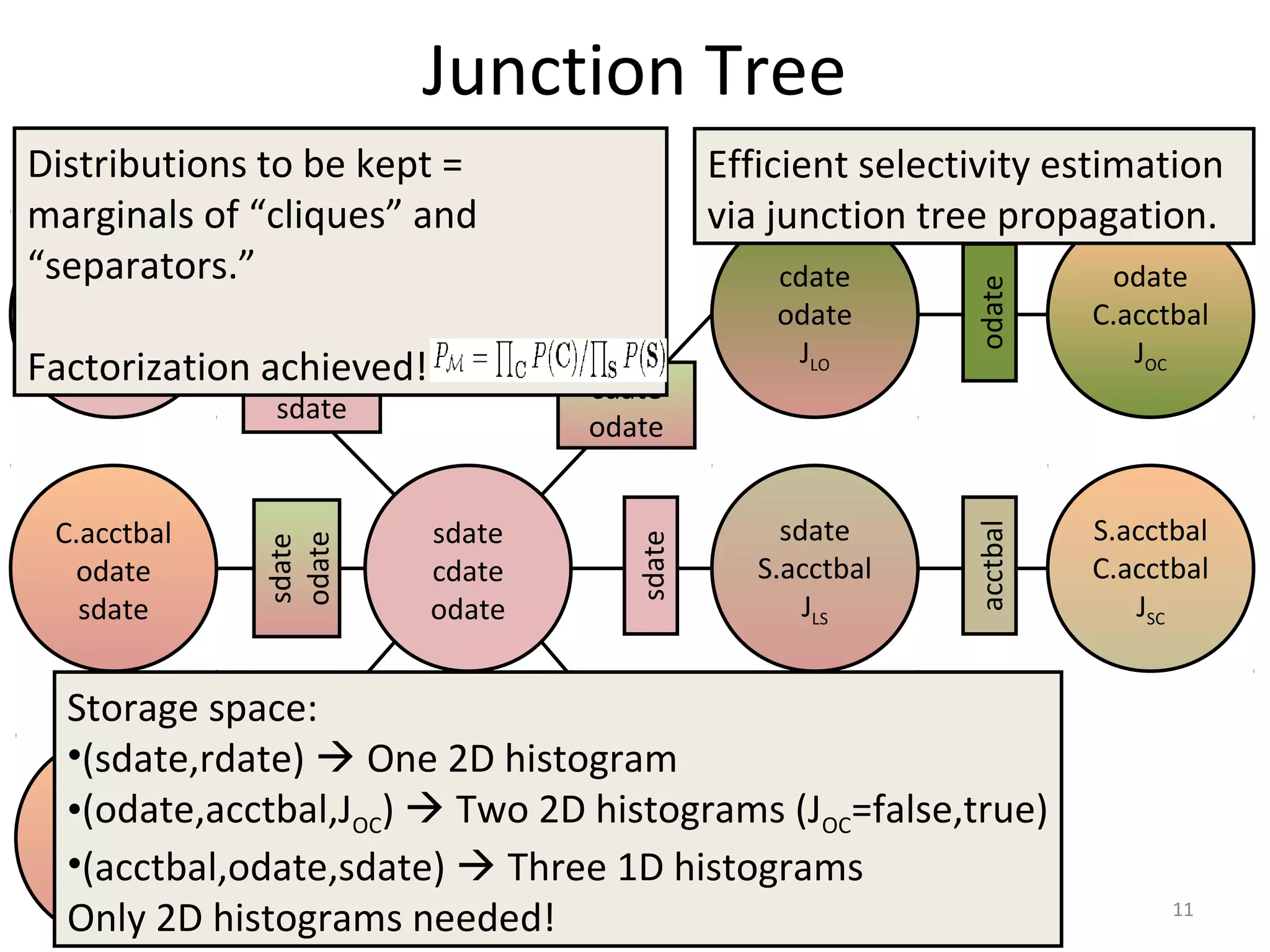
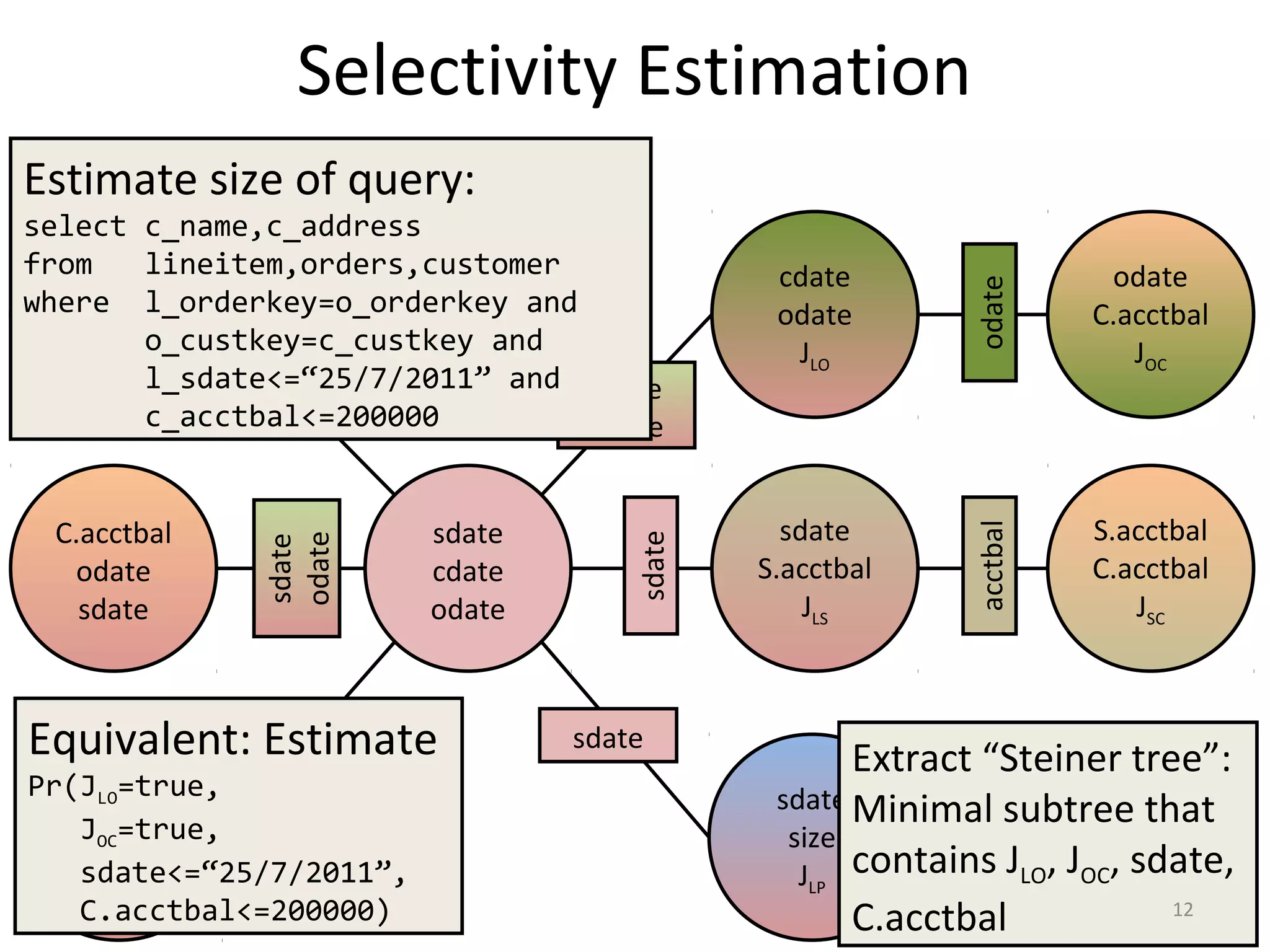
13. Selectivity Estimation
sdate
cdate
odate
cdate
odate
JLO
odate
acctbal
JOC
cdate
odate
odate
Estimate
Pr(JLO=true,
JOC=true,
sdate<=“25/7/2011”,
acctbal<=200000)
φ2=P(cdate,odate,JLO)
φ3=P(odate,acctbal,JOC)
φ1=P(sdate,cdate,odate)
μ12=P(cdate,odate)
μ23=P(odate)
1. Substitute
φ1
*
(cdate,odate)=
φ1[sdate<=“25/7/2011”]
φ2
*
(cdate,odate)=
φ2[JLO=true]
φ3
*
(odate)=
φ3[JOC=true,acctbal<=200000]
2. Multiply
φ12
*
(cdate,odate)=
φ1
*
φ2
*
/μ12
3. Marginalize
φ12
**
(odate)=
Σcdateφ12
*
4. Multiply
φ123
*
(odate)=
φ12
**
φ3
*
/μ23
5. Return
Σodateφ123
*
13

14. Implementation
• Model construction outside DBMS. Create distributions
with SQL queries.
– Stores junction tree as tables in PostgreSQL catalog.
• Graphical model foundation as PostgreSQL “nodes”.
– Probability distributions stored as equi-width multidimensional
histograms.
– Cliques, multiplication, division, marginalization.
– Junction tree, selectivity estimation algorithms
• Integration with PostgreSQL query optimizer.
– Load Steiner tree from catalog tables.
– Bypass PostgreSQL selectivity estimation functions.
14

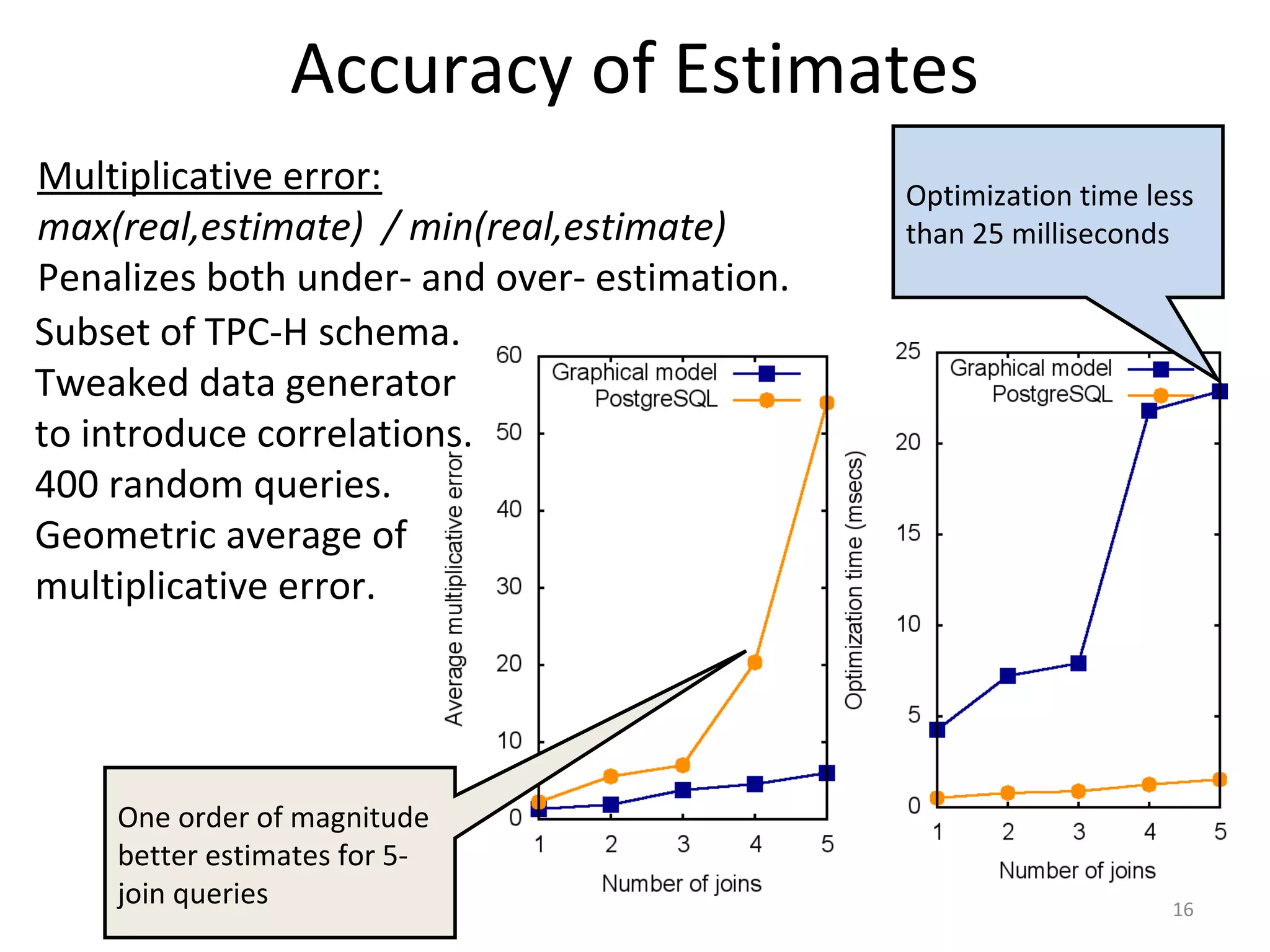
15. Impact of Capturing Correlations
select c_name,c_address
from lineitem,orders,customer
where l_orderkey=o_orderkey and o_custkey=c_custkey
and o_tprice in [t1,t2] and l_eprice in [e1,e2]
and c_acctbal in [b1,b2]
Avoid under-estimation
by capturing the price
correlation.
Estimates very close to
reality.
Optimizer picks different
plan than default PGSQL.
Huge impact in
execution time.
Can do selectivity
estimation efficiently.
Optimization time in
the range of 10s of
milliseconds
Cost of plans (intermediate tuples)
Execution & optimization times
15

16. Accuracy of Estimates
Multiplicative error:
max(real,estimate) / min(real,estimate)
Penalizes both under- and over- estimation.
Subset of TPC-H schema.
Tweaked data generator
to introduce correlations.
400 random queries.
Geometric average of
multiplicative error.
One order of magnitude
better estimates for 5-
join queries
Optimization time less
than 25 milliseconds
16

17. Conclusions and Future Work
• Conclusion
– Attribute value independence assumption unfounded
• Heuristic, not good enough
• Most frequent source of horrible plans
– Practical adaptation of graphical models implemented in
PostgreSQL
• Low overhead, good estimate quality
• Future work
– Specialized synopses
• Low-dimensional, minimize multiplicative error, error guarantees
after multiplication
– Incremental updates
• Building graphical model as a side-effect of query execution