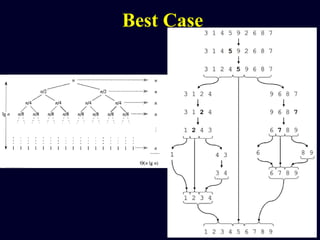
The quicksort algorithm works by recursively sorting arrays of data. It first selects a pivot element and partitions the array around the pivot so that all elements less than the pivot come before it and all elements greater than the pivot come after it. It then recursively sorts the sub-arrays to the left and right of the pivot until the entire array is sorted.

1. Quicksort Algorithm
• Basic idea
• Pick one element in the array, which will be the pivot.
• Make one pass through the array, called a partition step, re-arranging
the entries so that:
• the pivot is in its proper place.
• entries smaller than the pivot are to the left of the pivot.
• entries larger than the pivot are to its right.
• Recursively apply quicksort to the part of the array that is to the left of
the pivot,
and to the right part of the array.
• Here we don't have the merge step, at the end all the elements are in
the proper order.

2. Example
We are given array of n integers to sort:
40 20 10 80 60 50 7 30 100

3. Pick Pivot Element
There are a number of ways to pick the pivot element. In this
example, we will use the first element in the array:
40 20 10 80 60 50 7 30 100

4. Partitioning Array
Given a pivot, partition the elements of the array
such that the resulting array consists of:
1. One sub-array that contains elements >= pivot
2. Another sub-array that contains elements < pivot
The sub-arrays are stored in the original data array.
Partitioning loops through, swapping elements
below/above pivot.

5. 40 20 10 80 60 50 7 30 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

6. 40 20 10 80 60 50 7 30 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J
1. While data[i] <= data[pivot]
++i

7. 40 20 10 80 60 50 7 30 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J
1. While data[i] <= data[pivot]
++i

8. 40 20 10 80 60 50 7 30 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J
1. While data[i] <= data[pivot]
++i

9. 40 20 10 80 60 50 7 30 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J
1. While data[i] <= data[pivot]
++i
2. While data[i] > data[pivot]
--J

10. 40 20 10 80 60 50 7 30 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J

11. 40 20 10 80 60 50 7 30 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]

12. 40 20 10 30 60 50 7 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]

13. 40 20 10 30 60 50 7 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.

14. 40 20 10 30 60 50 7 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.

15. 40 20 10 30 60 50 7 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.

16. 40 20 10 30 60 50 7 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.

17. 40 20 10 30 60 50 7 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.

18. 40 20 10 30 60 50 7 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.

19. 1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

20. 1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

21. 1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

22. 1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

23. 1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

24. 1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

25. 1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

26. 1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

27. 1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

28. 1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]
40 20 10 30 7 50 60 80 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

29. 1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]
7 20 10 30 40 50 60 80 100pivot_index = 4
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

30. Partition Result
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
<= data[pivot] > data[pivot]

31. Recursion: Quicksort Sub-arrays
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
<= data[pivot] > data[pivot]

32. Recursion: Quicksort Sub-arrays
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
<= data[pivot] > data[pivot]
This Part will be solved
later

33. Recursion: Quicksort Sub-arrays
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]
This Part will be solved
later
pivot_index = 0
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

34. Recursion: Quicksort Sub-arrays
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]
This Part will be solved
later
pivot_index = 0
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

35. Recursion: Quicksort Sub-arrays
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]
This Part will be solved
later
pivot_index = 0
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

36. Recursion: Quicksort Sub-arrays
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]
This Part will be solved
later
pivot_index = 0
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

37. Recursion: Quicksort Sub-arrays
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]
This Part will be solved
later
pivot_index = 0
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

38. Recursion: Quicksort Sub-arrays
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]
This Part will be solved
later
pivot_index = 0
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

39. Recursion: Quicksort Sub-arrays
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]
This Part will be solved
later
pivot_index = 0

40. Recursion: Quicksort Sub-arrays
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]
This Part will be solved
later
pivot_index = 1

41. Recursion: Quicksort Sub-arrays
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]
This Part will be solved
later
pivot_index = 1
i
j

42. Recursion: Quicksort Sub-arrays
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]
This Part will be solved
later
pivot_index = 1
i
j1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

43. Recursion: Quicksort Sub-arrays
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]
This Part will be solved
later
pivot_index = 1
i
j1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

44. Recursion: Quicksort Sub-arrays
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]
This Part will be solved
later
pivot_index = 1
i
j1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

45. Recursion: Quicksort Sub-arrays
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]
This Part will be solved
later
pivot_index = 1
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

46. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]
This Part will be solved
later
pivot_index = 2
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

47. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]
This Part will be solved
later
pivot_index = 2

48. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]
This Part will be solved
later
pivot_index = 2

49. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]

50. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
pivot_index = 5

51. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
pivot_index = 5
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

52. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
pivot_index = 5
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

53. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
pivot_index = 5
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

54. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
pivot_index = 5
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

55. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
pivot_index = 5
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

56. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
pivot_index = 5
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

57. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
pivot_index = 5
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

58. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
pivot_index = 6
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

59. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
pivot_index = 6
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

60. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
pivot_index = 6
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

61. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
pivot_index = 6
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

62. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
pivot_index = 6
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

63. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
pivot_index = 6
i j
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

64. Recursion: Quicksort Sub-arrays
7 10 20 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
pivot_index = 6
1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]

65. Quicksort Analysis
• Assume that keys are random, uniformly
distributed.
• What is best case running time?

66. Quicksort Analysis
• Assume that keys are random, uniformly
distributed.
• What is best case running time?
– Recursion:
1. Partition splits array in two sub-arrays of size n/2
2. Quicksort each sub-array

67. Quicksort Analysis
• Assume that keys are random, uniformly
distributed.
• What is best case running time?
– Recursion:
1. Partition splits array in two sub-arrays of size n/2
2. Quicksort each sub-array
– Depth of recursion tree?

68. Quicksort Analysis
• Assume that keys are random, uniformly
distributed.
• What is best case running time?
– Recursion:
1. Partition splits array in two sub-arrays of size n/2
2. Quicksort each sub-array
– Depth of recursion tree? O(log2n)

69. Quicksort Analysis
• Assume that keys are random, uniformly
distributed.
• What is best case running time?
– Recursion:
1. Partition splits array in two sub-arrays of size n/2
2. Quicksort each sub-array
– Depth of recursion tree? O(log2n)
– Number of accesses in partition?

70. Quicksort Analysis
• Assume that keys are random, uniformly
distributed.
• What is best case running time?
– Recursion:
1. Partition splits array in two sub-arrays of size n/2
2. Quicksort each sub-array
– Depth of recursion tree? O(log2n)
– Number of accesses in partition? O(n)

71. Quicksort Analysis
• Assume that keys are random, uniformly
distributed.
• Best case running time: O(n log2n)

72. Quicksort Analysis
• Assume that keys are random, uniformly
distributed.
• Best case running time: O(n log2n)
• Worst case running time?

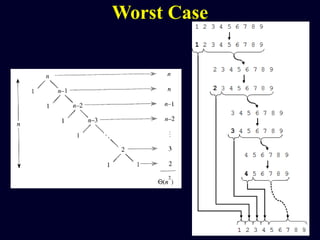
73. Quicksort: Worst Case
• Assume first element is chosen as pivot.
• Assume we get array that is already in
order:
2 4 10 12 13 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

74. 1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]
2 4 10 12 13 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

75. 1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]
2 4 10 12 13 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

76. 1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]
2 4 10 12 13 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

77. 1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]
2 4 10 12 13 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

78. 1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]
2 4 10 12 13 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

79. 1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]
2 4 10 12 13 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

80. 1. While data[i] <= data[pivot]
++i
2. While data[j] > data[pivot]
--J
3. If i < J
swap data[i] and data[j]
4. While J > i, go to 1.
5. Swap data[j] and data[pivot_index]
2 4 10 12 13 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]<= data[pivot]

81. Quicksort Analysis
• Assume that keys are random, uniformly
distributed.
• Best case running time: O(n log2n)
• Worst case running time?
– Recursion:
1. Partition splits array in two sub-arrays:
• one sub-array of size 0
• the other sub-array of size n-1
1. Quicksort each sub-array
– Depth of recursion tree?

82. Quicksort Analysis
• Assume that keys are random, uniformly
distributed.
• Best case running time: O(n log2n)
• Worst case running time?
– Recursion:
1. Partition splits array in two sub-arrays:
• one sub-array of size 0
• the other sub-array of size n-1
1. Quicksort each sub-array
– Depth of recursion tree? O(n)

83. Quicksort Analysis
• Assume that keys are random, uniformly
distributed.
• Best case running time: O(n log2n)
• Worst case running time?
– Recursion:
1. Partition splits array in two sub-arrays:
• one sub-array of size 0
• the other sub-array of size n-1
1. Quicksort each sub-array
– Depth of recursion tree? O(n)
– Number of accesses per partition?

84. Quicksort Analysis
• Assume that keys are random, uniformly
distributed.
• Best case running time: O(n log2n)
• Worst case running time?
– Recursion:
1. Partition splits array in two sub-arrays:
• one sub-array of size 0
• the other sub-array of size n-1
1. Quicksort each sub-array
– Depth of recursion tree? O(n)
– Number of accesses per partition? O(n)

85. Quicksort Analysis
• Assume that keys are random, uniformly
distributed.
• Best case running time: O(n log2n)
• Worst case running time: O(n2
)!!!

86. Quicksort Analysis
• Assume that keys are random, uniformly
distributed.
• Best case running time: O(n log2n)
• Worst case running time: O(n2
)!!!
• What can we do to avoid worst case?

87. Improved Pivot Selection
Pick median value of three elements from data array:
data[0], data[n/2], and data[n-1].
Use this median value as pivot.

88. Improving Performance of
Quicksort
• Improved selection of pivot.
• For sub-arrays of size 3 or less, apply brute
force search:
– Sub-array of size 1: trivial
– Sub-array of size 2:
• if(data[first] > data[second]) swap them
– Sub-array of size 3: left as an exercise.

89. Quicksort: Avoiding Worst Case
median= data [0], data [n/2], data [n-1]
Median = ( 2, 13,100)=pivot=13
2 4 10 12 13 50 57 63 100pivot_index = 4
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

90. Quicksort: Avoiding Worst Case
median= data [0], data [n/2], data [n-1]
Median = ( 2, 13,100)=pivot=13
13 4 10 12 2 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

91. Quicksort: Avoiding Worst Case
median= data [0], data [n/2], data [n-1]
Median = ( 2, 13,100)=pivot=13
13 4 10 12 2 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

92. Quicksort: Avoiding Worst Case
median= data [0], data [n/2], data [n-1]
Median = ( 2, 13,100)=pivot=13
13 4 10 12 2 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

93. Quicksort: Avoiding Worst Case
median= data [0], data [n/2], data [n-1]
Median = ( 2, 13,100)=pivot=13
13 4 10 12 2 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

94. Quicksort: Avoiding Worst Case
median= data [0], data [n/2], data [n-1]
Median = ( 2, 13,100)=pivot=13
13 4 10 12 2 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

95. Quicksort: Avoiding Worst Case
median= data [0], data [n/2], data [n-1]
Median = ( 2, 13,100)=pivot=13
13 4 10 12 2 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

96. Quicksort: Avoiding Worst Case
median= data [0], data [n/2], data [n-1]
Median = ( 2, 13,100)=pivot=13
13 4 10 12 2 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

97. Quicksort: Avoiding Worst Case
median= data [0], data [n/2], data [n-1]
Median = ( 2, 13,100)=pivot=13
13 4 10 12 2 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

98. Quicksort: Avoiding Worst Case
median= data [0], data [n/2], data [n-1]
Median = ( 2, 13,100)=pivot=13
13 4 10 12 2 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

99. Quicksort: Avoiding Worst Case
median= data [0], data [n/2], data [n-1]
Median = ( 2, 13,100)=pivot=13
13 4 10 12 2 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

100. Quicksort: Avoiding Worst Case
median= data [0], data [n/2], data [n-1]
Median = ( 2, 13,100)=pivot=13
13 4 10 12 2 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

101. Quicksort: Avoiding Worst Case
median= data [0], data [n/2], data [n-1]
Median = ( 2, 13,100)=pivot=13
13 4 10 12 2 50 57 63 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

102. Quicksort: Avoiding Worst Case
median= data [0], data [n/2], data [n-1]
Median = ( 2, 13,100)=pivot=13
2 4 10 12 13 50 57 63 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

103. Quicksort: Avoiding Worst Case
median= data [0], data [n/2], data [n-1]
Median = ( 2, 13,100)=pivot=13
2 4 10 12 13 50 57 63 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i J

104. Feature of the Quick Sort
1. Similar to mergesort - divide-and-conquer
recursive algorithm
2. One of the fastest sorting algorithms
3. Average running time O(NlogN)
4. Worst-case running time O(N2
)

105. Good points
•It is in-place since it uses only a small auxiliary
stack.
•It requires only n log(n) time to sort n items.
•It has an extremely short inner loop
•This algorithm has been subjected to a thorough
mathematical analysis, a very precise statement
can be made about performance issues.

106. Bad Points
•It is recursive. Especially if recursion is not
available, the implementation is extremely
complicated.
•It requires quadratic (i.e., n2
) time in the worst-
case.
•It is fragile i.e., a simple mistake in the
implementation can go unnoticed and cause it to
perform badly

107. Quick sort works by partitioning a given array A[p . . r] into two
non-empty sub array A[p . . q] and A[q+1 . . r] such that every key
in A[p . . q] is less than or equal to every key in A[q+1 . . r]. Then
the two subarrays are sorted by recursive calls to Quick sort. The
exact position of the partition depends on the given array and
index q is computed as a part of the partitioning procedure

108. QuickSort
If p < r then
q =Partition (A, p, r)
Recursive call to Quick
Sort (A, p, q)
Recursive call to Quick
Sort (A, q + r, r)
Note that to sort entire array,
the initial call Quick Sort (A,
1, length[A])
int partition( A, p, r)
1. i←p,
2. j ←r;
3. q ← A[(p+q/2)];
4.
5. WHILE i <= j
6. while A[i] < q
7. i ←i+1;
8. END-While
9. WHILE arr[j] > q
10. j ←j-1;
END-While
11. if i <= j
12. then
13. swap ( A[i] , A[j])
14. i ←i+1
15. j ←j-1;
16. end if
17. END-WHILE
18. return i;

109. Running time complexity
• Partition procedure has O(n)
• Quick sort divides the array into sub array,
whenever division is involved, complexity
will be O(log n)
• Therefore O (n-logn) quick sort complexity
1. http://stackoverflow.com/questions/9556782/find-theta-notation-o
2. http://stackoverflow.com/questions/11032015/how-to-
find-time-complexity-of-an-algorithm

110. • Code in Sharp In visual studio

111. Array of Same Elements.
• Since all the elements are equal, the "less than or equal"
teat in lines 6 and 8 in the PARTITION (A, p, r) will
always be true. this simply means that repeat loop all stop
at once. Intuitively, the first repeat loop moves j to the left;
the second repeat loop moves i to the right. In this case,
when all elements are equal, each repeat loop
moves i and j towards the middle one space. They meet in
the middle, so q= Floor(p+r/2). Therefore, when all
elements in the array A[p . . r] have the same value equal
to Floor(p+r/2)
Practice for Students

112. Best Case

113. Performance of Quick Sort:
Best Case
• Best Case
• Partition call O(n)
• two recursive calls each will have
O(n/2)
• T(n) = O(n) +2 T(n/2)
• Apply Master theorem
– a= 2, b=2, C=1, k=0;
– T(n)= O(n log n)

114. Performance of Quick Sort:
Best Case, Second MethodDivide by N:
T(N) / N = T(N/2) / (N/2) + c
Telescoping:
T(N/2) / (N/2) = T(N/4) / (N/4) + c
T(N/4) / (N/4) = T(N/8) / (N/8) + c
……
T(2) / 2 = T(1) / (1) + c
Add all equations:
T(N) / N + T(N/2) / (N/2) + T(N/4) / (N/4) + …. + T(2) / 2 =
= (N/2) / (N/2) + T(N/4) / (N/4) + … + T(1) / (1) + c.logN
After crossing the equal terms:
T(N)/N = T(1) + cLogN = 1 + cLogN
T(N) = N + NcLogN
Therefore T(N) = O(NlogN)

115. Worst Case

116. Worst Case
Pay attention, the quicksort algorithm worst case scenario is when you
have two subproblems of size 0 and n-1. In this scenario, you have this
recurrence equations for each level:
T(n) = T(n-1) + T(0) < -- at first level of tree
T(n-1) = T(n-2) + T(0) < -- at second level of tree
T(n-2) = T(n-3) + T(0) < -- at third level of tree
The sum of costs at each level is an arithmetic serie:
T(N) + T(N-1) + T(N-2) + … + T(2) =
= T(N-1) + T(N-2) + … + T(2) + T(1) + c(N) + c(N-1) + c(N-2) + …
+ c.2
T(N) = T(1) + c(2 + 3 + … + N)
T(N) = 1 + c(N(N+1)/2 -1) Therefore T(N) = O(N2
)

117. Balance Partitioning
• T(n) <= T(9n/10) + T(n/10) + cn
assume the partitioning algorithm always
produces 9:1 splitting ratio, which
appears unbalanced. We have:
he average-case running time of quicksort is much
closer to the best case than to the worst case

118. Average Case
• T(n) <= T(9n/10) + T(n/10) + cn
assume the partitioning algorithm always
produces 9:1 splitting ratio, which
appears unbalanced. We have:
he average-case running time of quicksort is much
closer to the best case than to the worst case

119. Average Case
he average-case running time of quicksort is much
closer to the best case than to the worst case
(a) Two levels of a recursion tree for quicksort. The partitioning
at the root costs n and produces a "bad" split: two subarrays of
sizes 1 and n - 1. The partitioning of the subarray of size n - 1
costs n - 1 and produces a "good" split: two subarrays of size (n -
1)/2
good
bad

120. Average Case
The average value of T(i) is 1/N times the sum of T(0)
through T(N-1)
1/N S T(j), j = 0 thru N-1
T(N) = 2/N (S T(j)) + cN
Multiply by N
NT(N) = 2(S T(j)) + cN*N

121. Average CaseMultiply by N
NT(N) = 2(S T(j)) + cN*N
To remove the summation, we rewrite the equation for N-1:
(N-1)T(N-1) = 2(S T(j)) + c(N-1)2, j = 0 thru N-2
and subtract:
NT(N) - (N-1)T(N-1) = 2T(N-1) + 2cN -c
Prepare for telescoping. Rearrange terms, drop the insignificant c:
NT(N) = (N+1)T(N-1) + 2cN

122. Average CaseDivide by N(N+1):
T(N)/(N+1) = T(N-1)/N + 2c/(N+1)
Telescope:
T(N)/(N+1) = T(N-1)/N + 2c/(N+1)
T(N-1)/(N) = T(N-2)/(N-1)+ 2c/(N)
T(N-2)/(N-1) = T(N-3)/(N-2) + 2c/(N-1)
….
T(2)/3 = T(1)/2 + 2c /3

123. Average CaseDivide by N(N+1):
T(N)/(N+1) = T(N-1)/N + 2c/(N+1)
Telescope:
T(N)/(N+1) = T(N-1)/N + 2c/(N+1)
T(N-1)/(N) = T(N-2)/(N-1)+ 2c/(N)
T(N-2)/(N-1) = T(N-3)/(N-2) + 2c/(N-1)
….
T(2)/3 = T(1)/2 + 2c /3

124. Average Case
Add the equations and cross equal terms:
T(N)/(N+1) = T(1)/2 +2c S (1/j), j = 3 to N+1
T(N) = (N+1)(1/2 + 2c S(1/j))
The sum S (1/j), j =3 to N-1, is about LogN
Thus T(N) = O(NlogN)

125. ConclusionAdvantages:
•One of the fastest algorithms on average.
•Does not need additional memory (the sorting takes place in the array - this is
called in-place processing). Compare with mergesort: mergesort needs
additional memory for merging.
Disadvantages: The worst-case complexity is O(N2
)
Applications:
Commercial applications use Quicksort - generally it runs fast, no additional
memory,
this compensates for the rare occasions when it runs with O(N2
)
Never use in applications which require guaranteed response time:
•Life-critical (medical monitoring, life support in aircraft and space craft)
•Mission-critical (monitoring and control in industrial and research plants
handling dangerous materials, control for aircraft, defense, etc)
unless you assume the worst-case response time.
has O(nlog n) performance: can we do any better?
In general, the answer is no.

126. Conclusion
Comparison with heapsort:
•both algorithms have O(NlogN) complexity
•quicksort runs faster, (does not support a heap tree)
•the speed of quick sort is not guaranteed
Comparison with mergesort:
•mergesort guarantees O(NlogN) time, however it requires
additional memory with size N.
•quicksort does not require additional memory, however
the speed is not quaranteed
•usually mergesort is not used for main memory sorting,
only for external memory sorting.
•So far, our best sorting algorithm