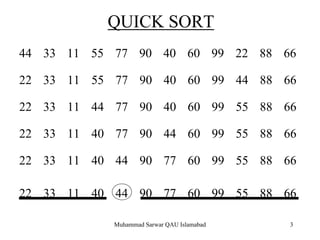
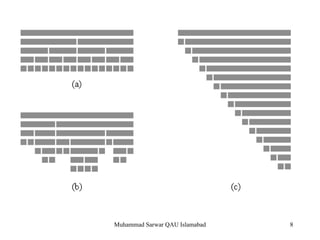
The document discusses quicksort and partition algorithms for sorting arrays. Quicksort works by recursively dividing an array into smaller sub-arrays by partitioning them based on a pivot value and sorting them. The partition algorithm divides an array into two partitions based on element values relative to the pivot. The performance of quicksort depends on how balanced the partitions are at each step.

1. Muhammad Sarwar QAU Islamabad 1
QUICK SORT
QUICKSORT (A, p, r)
1. if p < r
2. then q ← PARTITION(A, p, r)
3. QUICKSORT(A,p, q-1 )
4. QUICKSORT(A,q+1,r )

2. Muhammad Sarwar QAU Islamabad 2
PARTITION
PARTITION(A, p, r)
1. x←A[r]
2. i ← p-1
3. for j←p to r-1
4. if A[j]≤x then
5. i←i+1
6. exchange A[i]↔a[j]
7. exchange A[i+1]↔A[r]
8. return i+1

3. Muhammad Sarwar QAU Islamabad 3
QUICK SORT
668822996040907755113344
668844996040907755113322
668855996040907744113322
668855996044907740113322
668855996077904440113322
668855996077904440113322

4. Muhammad Sarwar QAU Islamabad 4
PARTITION
PARTITION (A, p, r)
1. x←A[p], i ←p-1, j ←r+1
2. while TRUE
3. do repeat j ←j - 1
4. until A[j]≤ x
5. repeat i ←i+1
6. until A[i]≥ x
7. if i<j
8. then exchange A[i]↔A[j]
9. else return j

5. Muhammad Sarwar QAU Islamabad 5
PARTITION
PARTITION (A, p, r)
1. x←A[p], i ←p-1, j ←r+1
2. while TRUE
3. do repeat j ←j - 1
4. until A[j]≤ x
5. repeat i ←i+1
6. until A[i]≥ x
7. if i<j
8. then exchange A[i]↔A[j]
9. else return j

6. Muhammad Sarwar QAU Islamabad 6
PARTITION
1. left←beg, right ← end, loc ← beg
2. [SCAN FROM RIGHT TO LEFT]
a) repeat while a [loc]<=a [right] & loc!=right
right ← right-1
b) if loc=right then return loc
c) if A [loc]>A [right] then
i. interchange A [loc] & A [right]
ii. loc ← right go to step 3
3. [SCAN FROM LEFT TO RIGHT]
a) repeat while A [left]<=A [loc] & left!=loc
left ← left+1
b) if loc=left then return loc
c) if A [left]>A [loc] then
i. interchange A [left] & A [loc]
ii. loc ← left, go to step 2

7. Muhammad Sarwar QAU Islamabad 7
ANALYSIS OF QUICK SORT
• Running time of quick sort depends on
whether the partitioning is balanced or
unbalanced
• The balancing of partition depends on which
elements are used
• If partitioning is balanced the running time
of quick sort is as fast as merge sort
• If partitioning is unbalanced the algorithm
runs as slow as insertion sort
• In worst case the partitions have size 1 & n-1
• In best case the partitions have size n/2

8. Muhammad Sarwar QAU Islamabad 8

9. Muhammad Sarwar QAU Islamabad 9
ANALYSIS OF QUICK SORT
WORST CASE
)()(
2
)1(
)1()(
.....
.....
)()1()2()3()(
)()1()2()(
)()1()(
2
1
nnT
nn
knT
nnnnTnT
nnnTnT
nnTnT
n
k
Θ=
+
=+Θ=
Θ+−Θ+−Θ+−=
Θ+−Θ+−=
Θ+−=
∑=

10. Muhammad Sarwar QAU Islamabad 10
ANALYSIS OF QUICK SORT
BEST CASE
)lg()(
)lg()(
oremmaster theof2Case)(
)()(
2,2
)()2/(2)(
log
log
2loglog 2
nnnT
nnnT
nnf
nnf
nnn
ba
nnTnT
a
a
a
b
b
b
Θ=⇒
Θ=⇒
=⇒
Θ=
==
==
Θ+=

11. Muhammad Sarwar QAU Islamabad 11
QUICK SORT
• What value of q does PARTITION
return when all elements in the array
A[p…r] have the same value?
• q = ⎣(p+r)/2⎦

12. Muhammad Sarwar QAU Islamabad 12
QUICK SORT
Suppose the partitions are in n/10 and 9n/10 what is
the running time?
We can make a tree to see the behavior
The recurrence is
T(n)=T(n/10)+T(9n/10)+Θ(n)

13. Muhammad Sarwar QAU Islamabad 13

14. Muhammad Sarwar QAU Islamabad 14
Q. Suppose that the splits at every level of quick sort are in proportion
1 – α to α where 0<α<=1/2 is a constant. Show that the minimum
depth of a leaf in the recursion tree is approximately –lgn/lgα and
maximum depth is approximately –lgn/lg(1 – α)
Ans:-If we expand the tree the side of α will end before the side of 1–α
)1lg(
lg
)1(log
log
)1(log1log
log
)1/(1log
log
log )1/(1
αα
αα
α
−
−=
−
−=
−−
=
−
=−
nn
nn
n
b
b
bb
b
b
b
αααα
α
lg
lg
log
log
log1log
log
/1log
log
log /1
nnnn
n
b
b
bb
b
b
b
−=−=
−
==