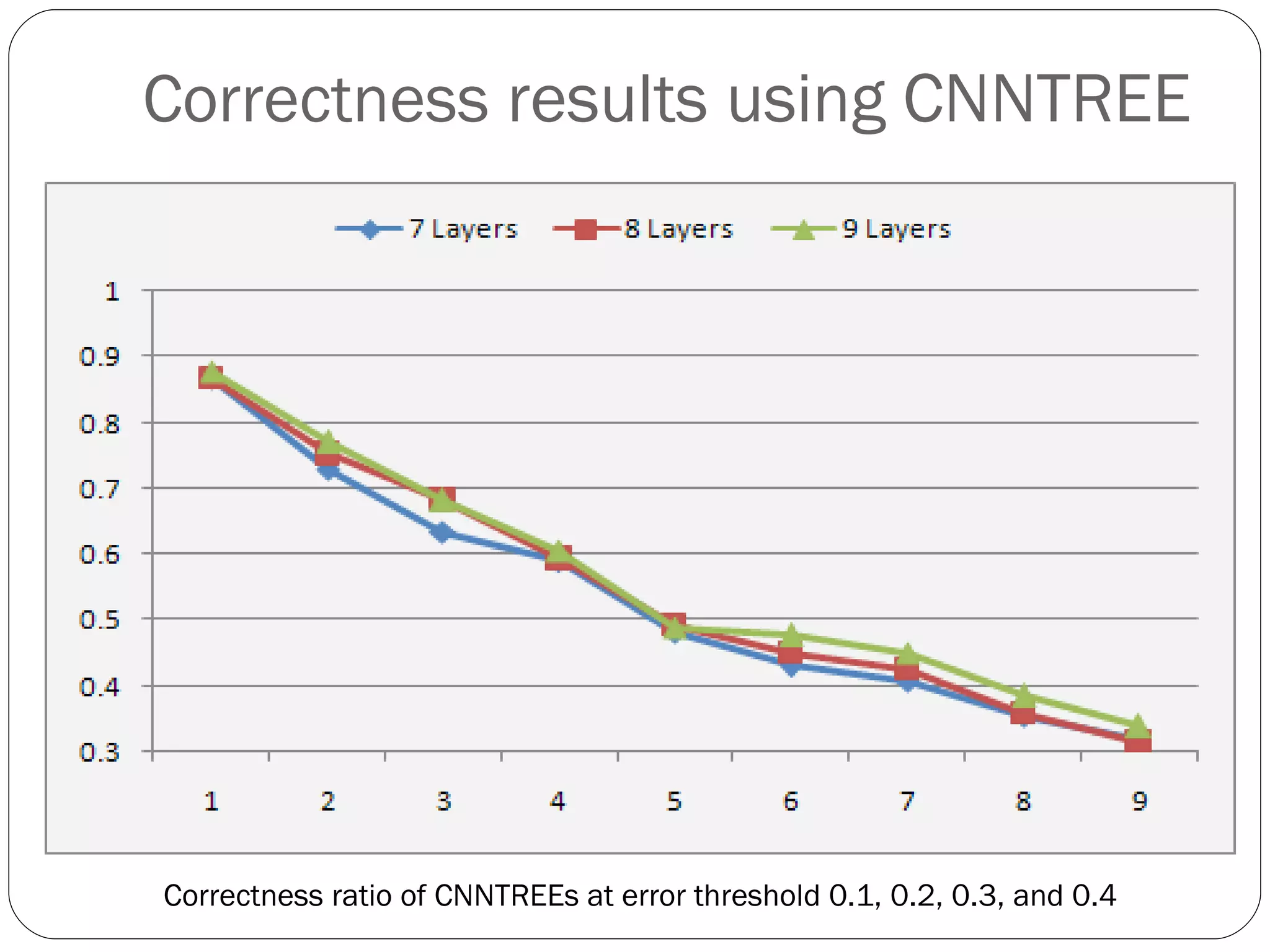
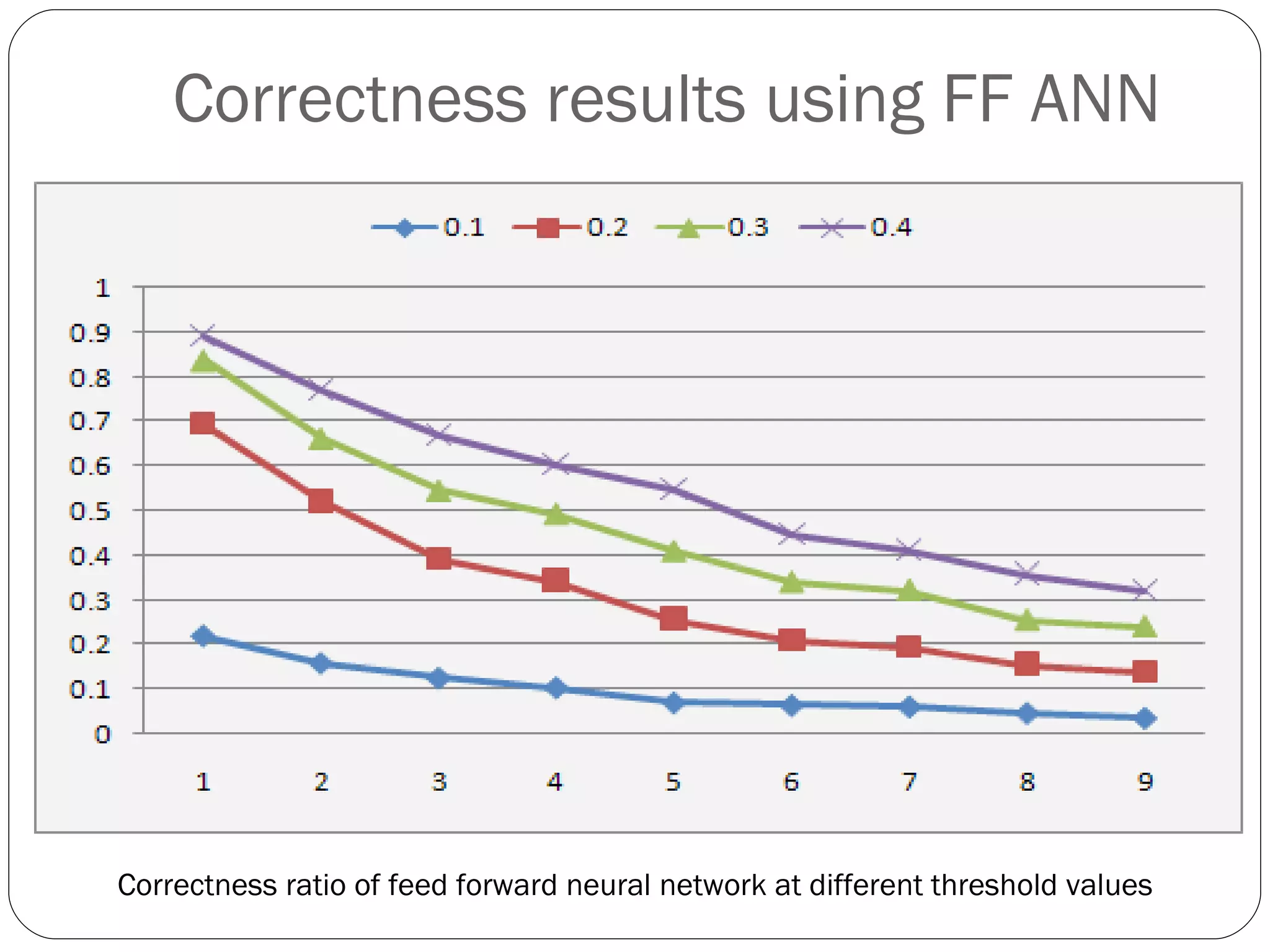
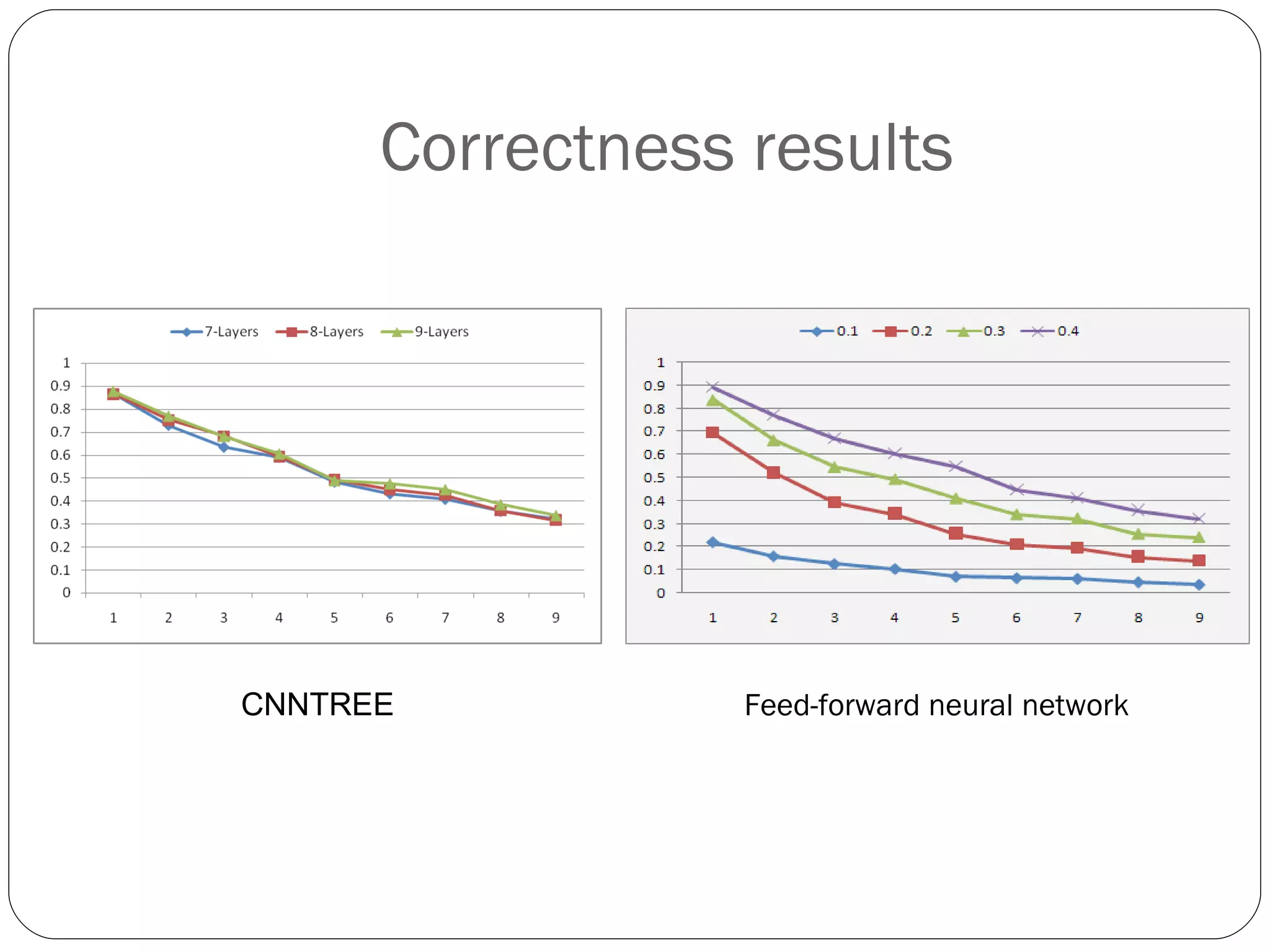
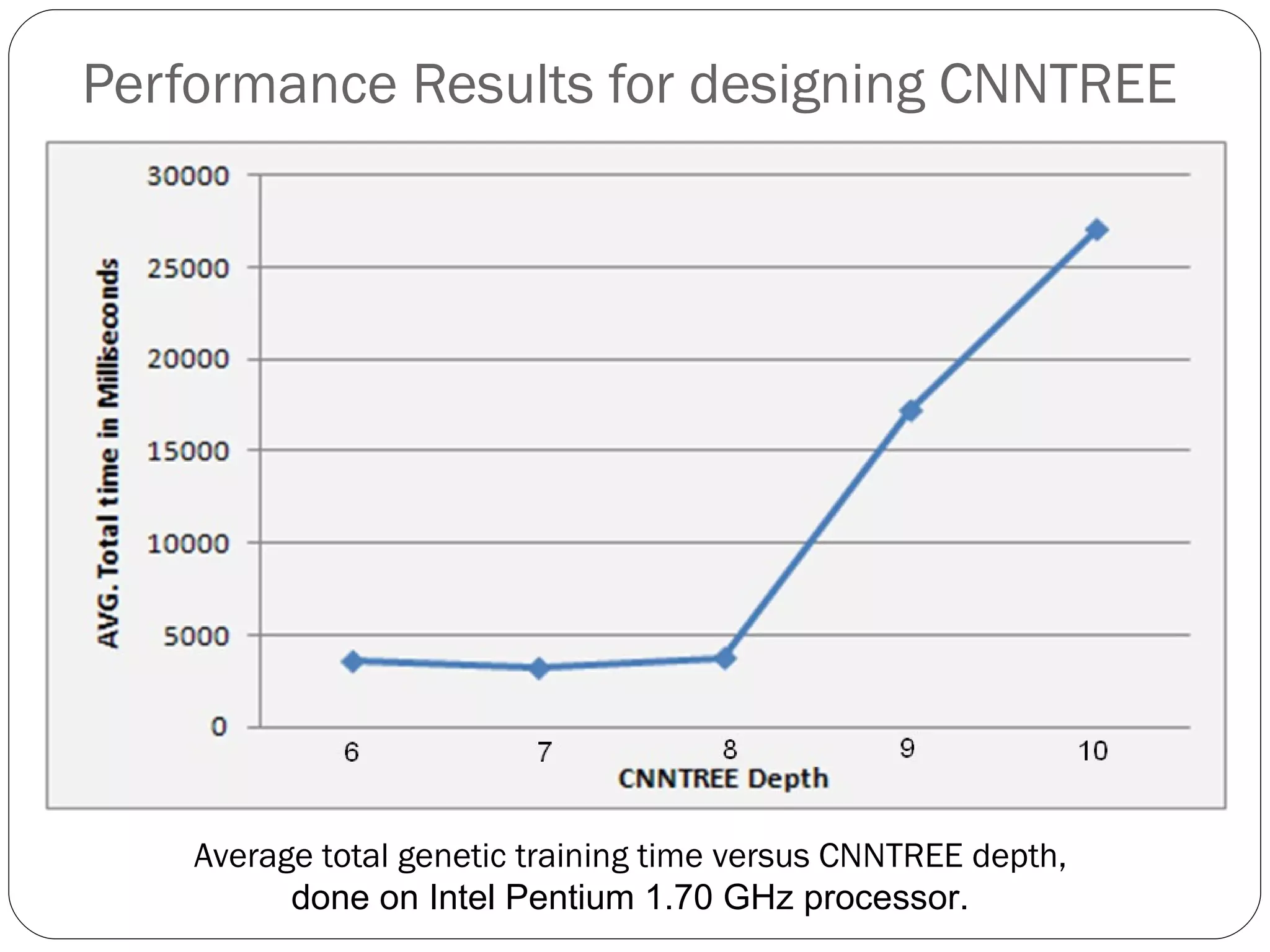
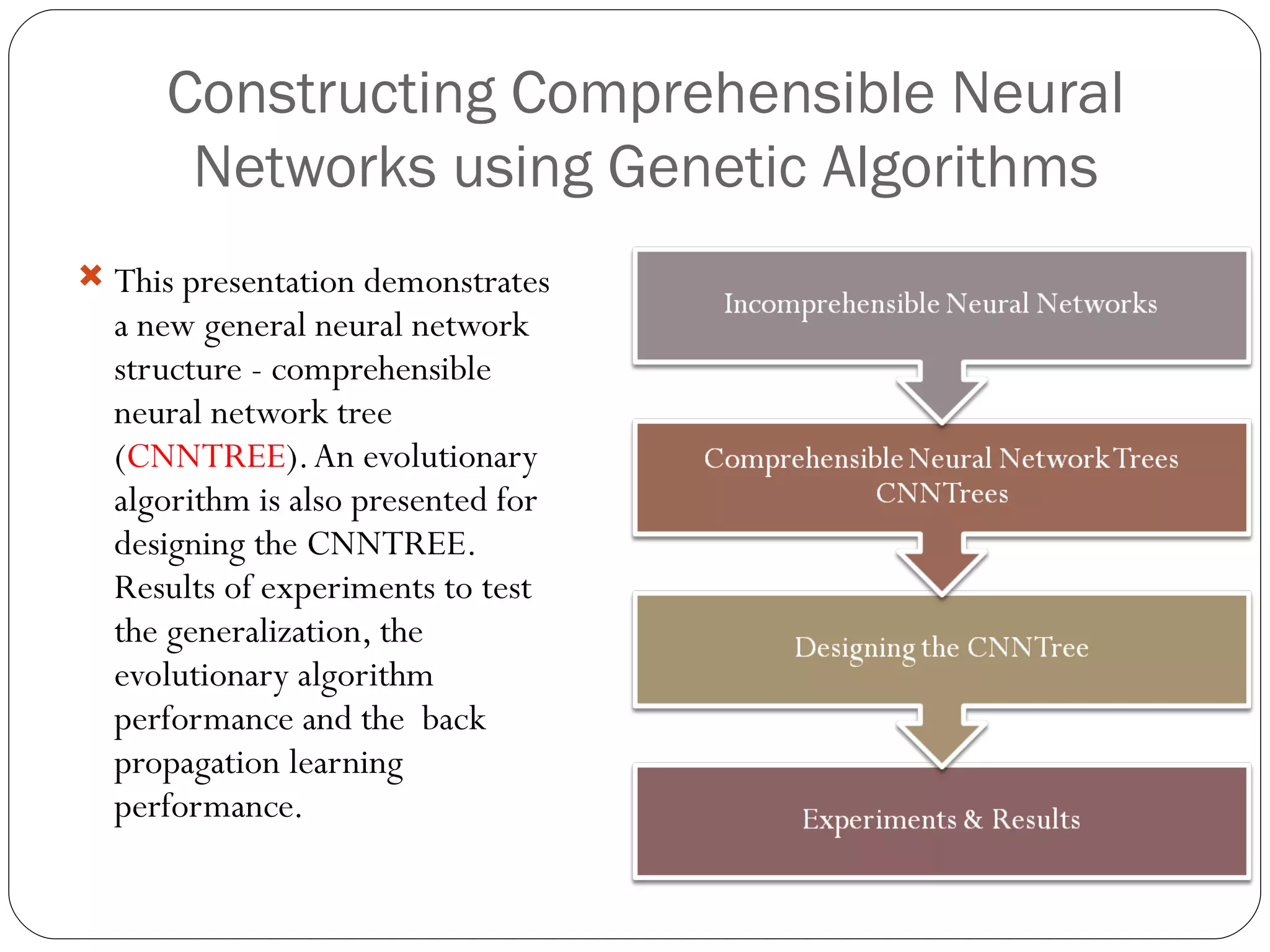
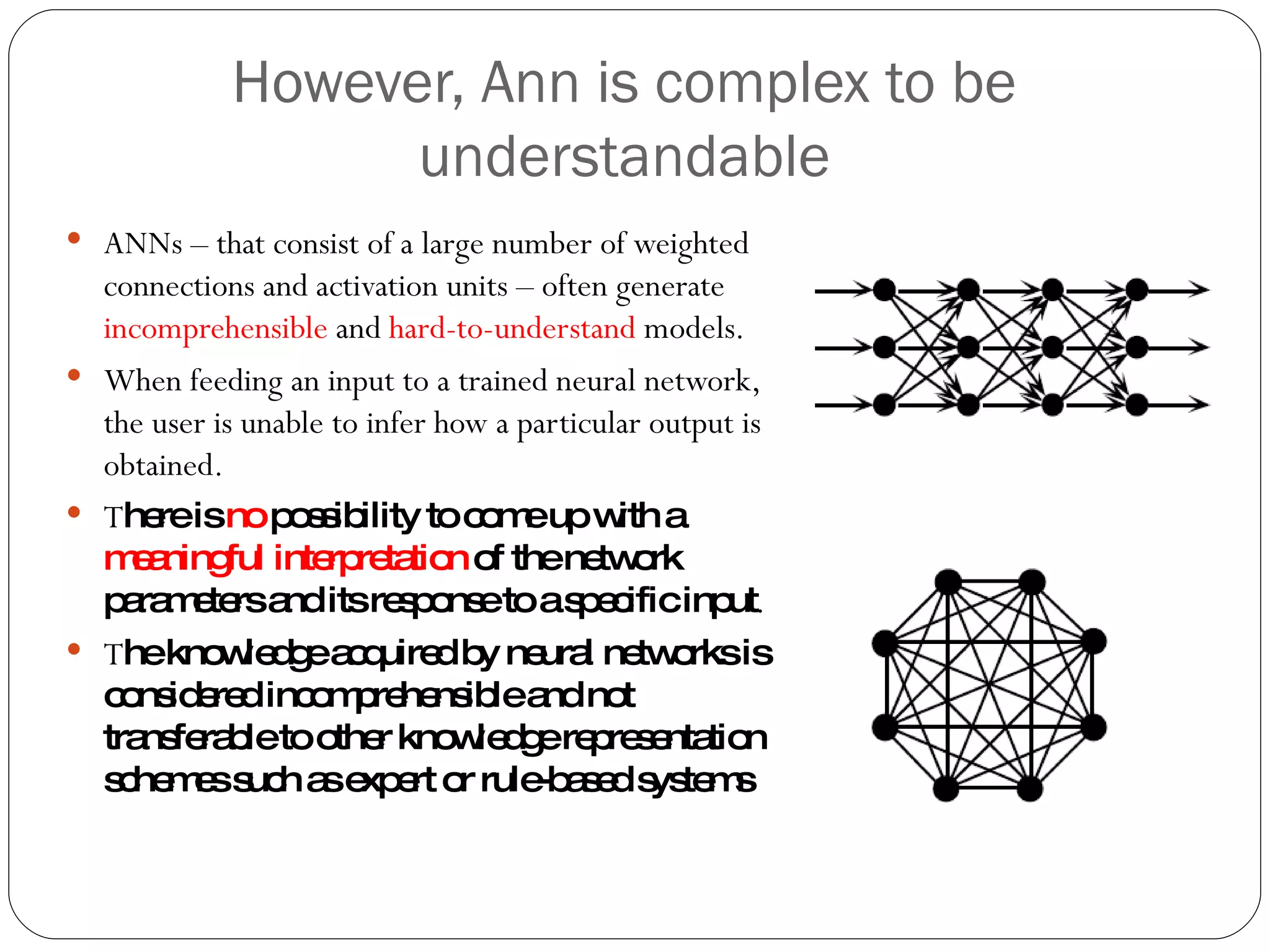
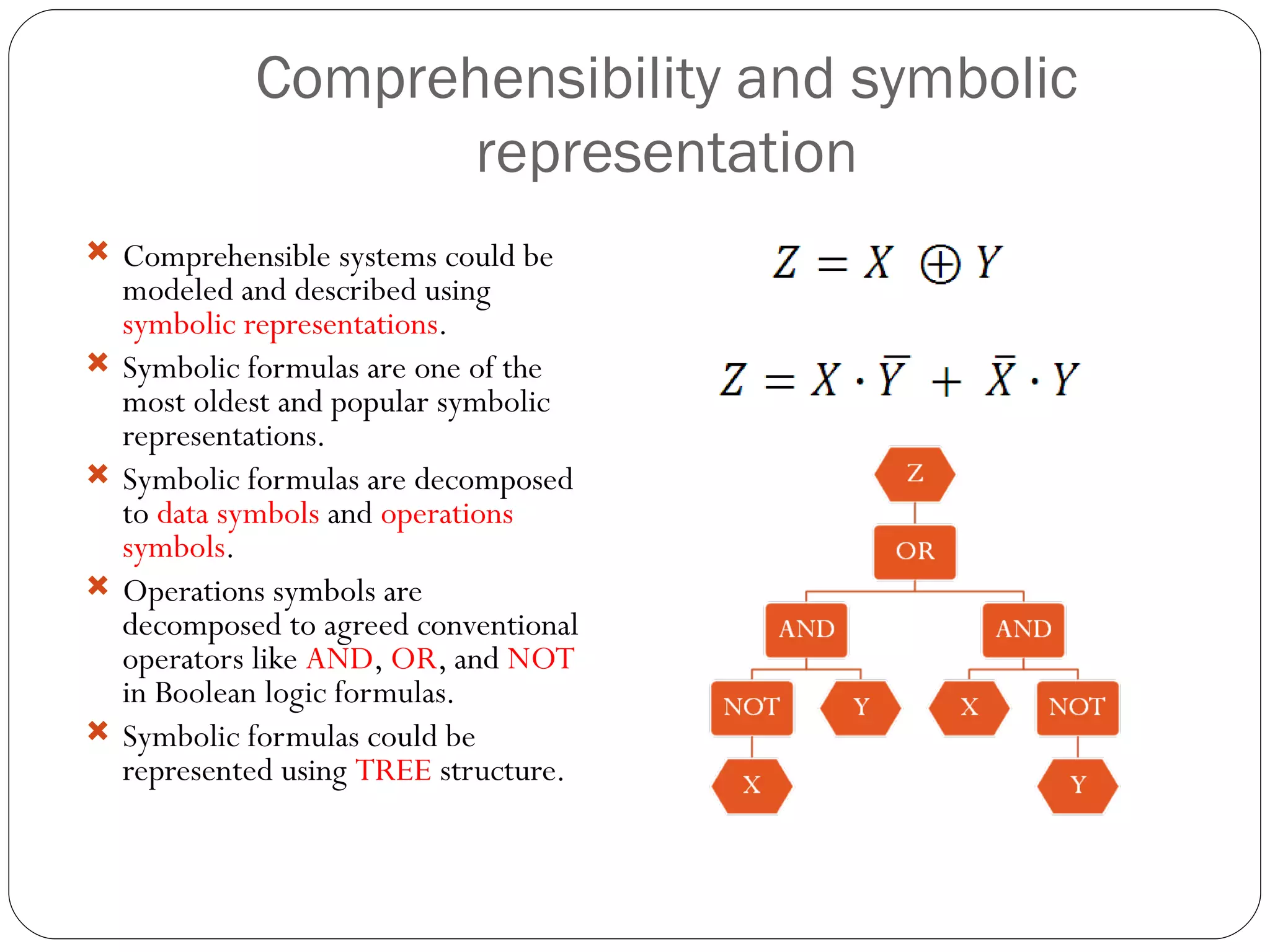
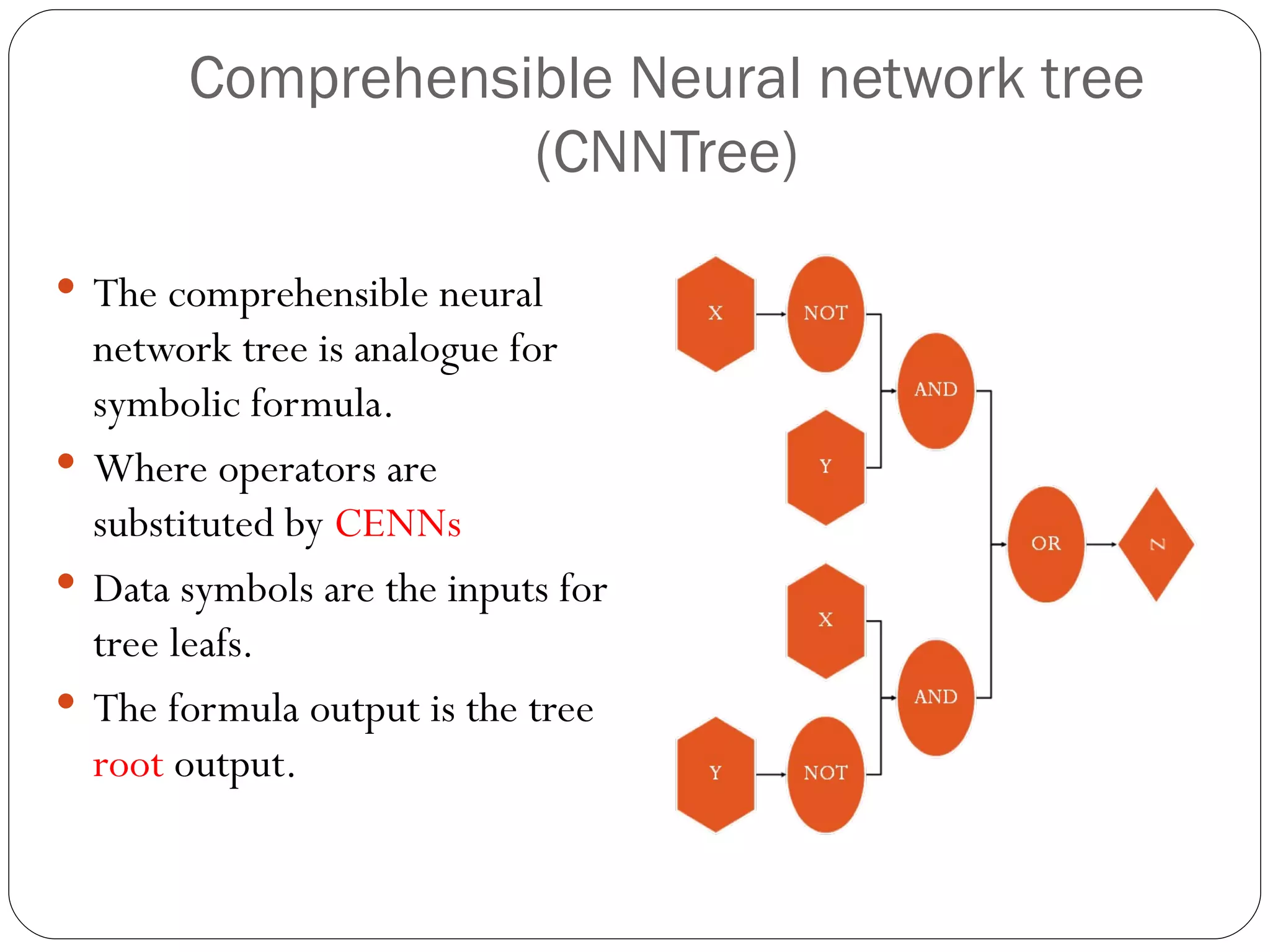
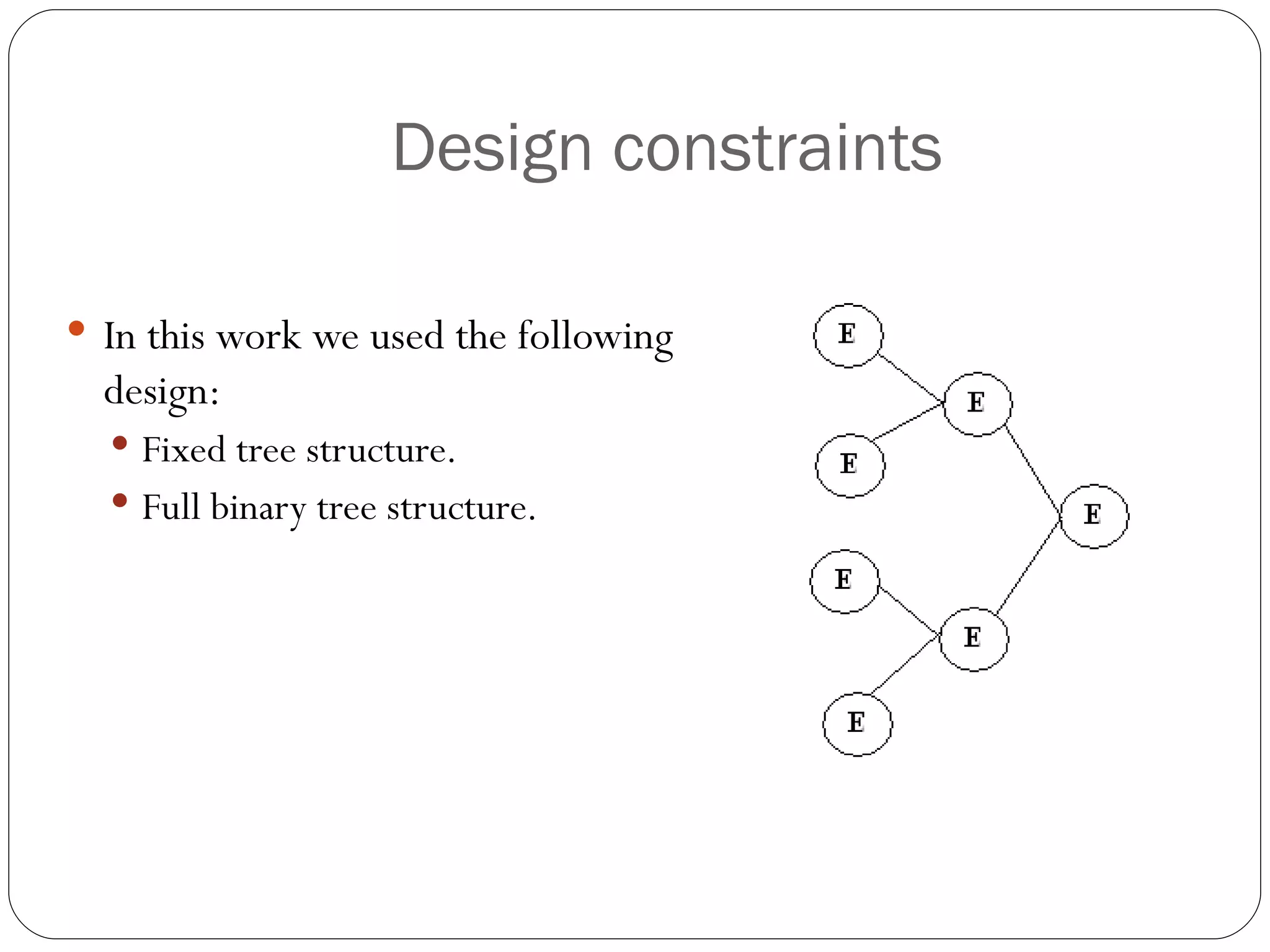
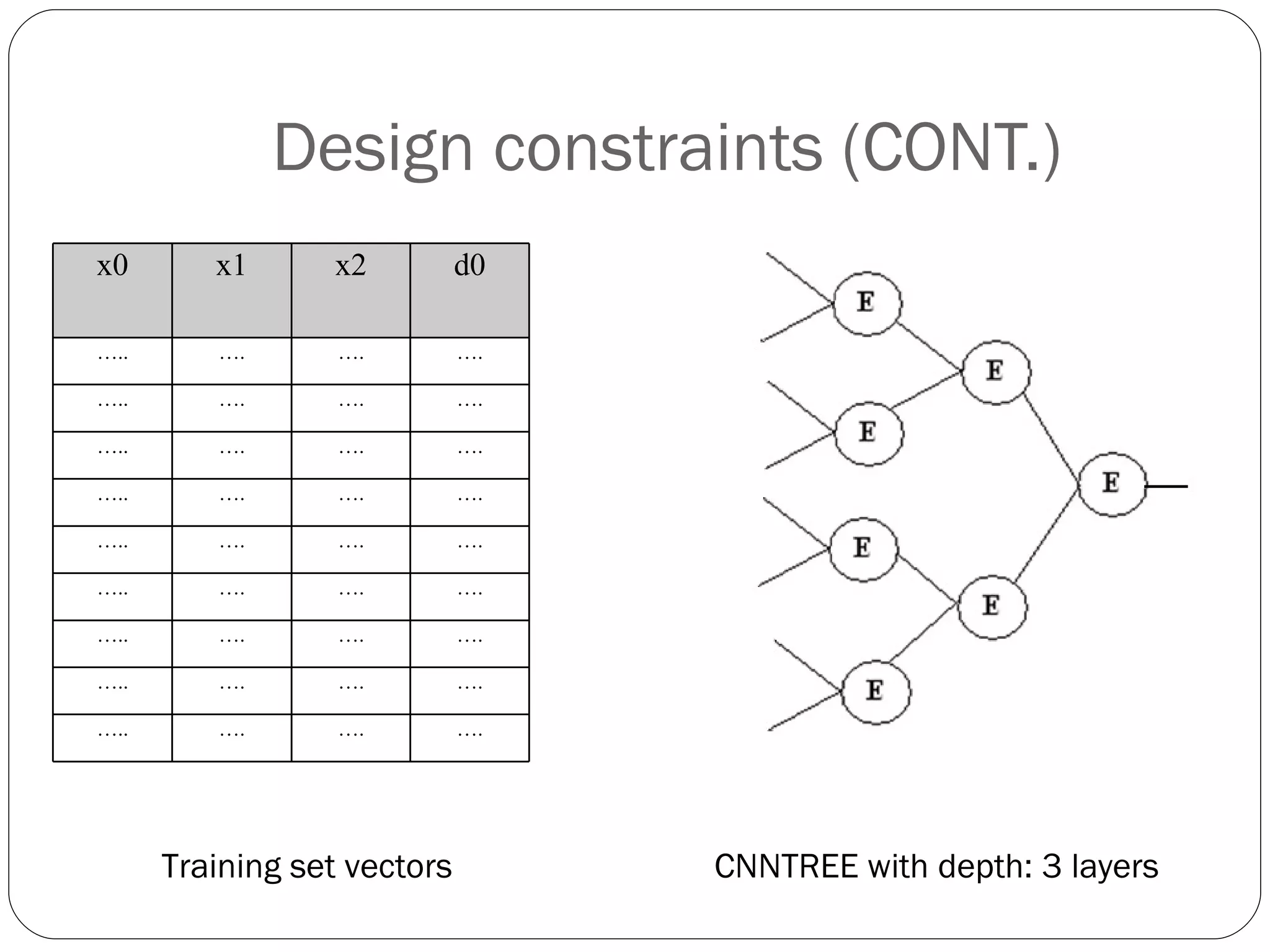
The document presents a master's thesis on constructing comprehensible neural networks using genetic algorithms, introducing a novel structure called the comprehensible neural network tree (CNNTREE). It discusses the challenges of interpreting traditional artificial neural networks and proposes a design that enhances understandability through symbolic representations. Experimental results demonstrate the CNNTREE's comparable generalization performance in digit recognition tasks while offering improved interpretability over conventional neural networks.

1. Constructing Comprehensible Neural Networks using Genetic Algorithms By Amr Kamel Ahmed El-Sayed Helwan University, Faculty of Engnieering, Department of Communications, Electronics, and Computers بناء شبكات عصابية سهلة التفسير باستخدام الخواريزمات الجينية Master Thesis Under Supervision of: Prof: Sayed Mostafa Saad Dr: Alaa Hamdy

2. PRIA-8-2007 8th International Conference on PATTERN RECOGNITION and IMAGE ANALYSIS: NEW INFORMATION TECHNOLOGIES. INTERNATIONAL ASSOCIATION FOR PATTERN RECOGNITION (IAPR). Paper Title “ EVOLVING COMPREHENSIBLE NEURAL NETWORK TREES USING GENETIC ALGORITHMS ”. Conference proceeding Volume 1, pages [186 - 190]. Accepted for publish in international journal. Would be published in NO 4. Vol.18. English papers are published in Springer. Paper Title “ EVOLVING COMPREHENSIBLE NEURAL NETWORK TREES USING GENETIC ALGORITHMS ”. Pattern Recognition and Image Analysis. Advances in Mathematical Theory and Applications

3. Constructing Comprehensible Neural Networks using Genetic Algorithms This presentation demonstrates a new general neural network structure - comprehensible neural network tree ( CNNTREE ). An evolutionary algorithm is also presented for designing the CNNTREE. Results of experiments to test the generalization, the evolutionary algorithm performance and the back propagation learning performance.

4. Incomprehensible Neural Networks

5. ANN solves various classes of problems ANNs are well suitable to solve various classes of problems in knowledge discovery field. They are applied successfully to the following categories: function approximation , regression analysis , time series prediction , classification , data clustering and data filtering . The parallel structure of neural networks makes them suitable for online learning within real time constraints . Simple and cheap units, that enables us to produce relatively cheap parallel processor that consists of massive number of units.

6. However, Ann is complex to be understandable ANNs – that consist of a large number of weighted connections and activation units – often generate incomprehensible and hard-to-understand models. When feeding an input to a trained neural network, the user is unable to infer how a particular output is obtained. T here is no possibility to come up with a meaningful interpretation of the network parameters and its response to a specific input . T he knowledge acquired by neural networks is considered incomprehensible and not transferable to other knowledge representation schemes such as expert or rule-based systems

7. Why querying comprehensibility ? Easy to be modeled and understood. Easy to be maintained and supported. Easy to be developed and enhanced. Easy to be transferred to other knowledge representations such as expert rule-based systems.

8. Comprehensible Neural Network Trees (CNNTrees)

9. Comprehensibility and symbolic representation Comprehensible systems could be modeled and described using symbolic representations . Symbolic formulas are one of the most oldest and popular symbolic representations. Symbolic formulas are decomposed to data symbols and operations symbols . Operations symbols are decomposed to agreed conventional operators like AND , OR , and NOT in Boolean logic formulas. Symbolic formulas could be represented using TREE structure.

10. Comprehensible Expert Neural network (CENN) In the XOR example, we selected a simple neural network to be trained for every conventional operation AND , OR , and NOT . This simple neural network that corresponds to the agreed conventional operations are called Comprehensible Expert Neural Network ( CENN ). The collection of CENNs that is used for building the tree is called Comprehensible Expert Neural Network Library ( CENNL ). Comprehensible Expert Neural Network Library CENNL

11. Comprehensible Neural network tree (CNNTree) The comprehensible neural network tree is analogue for symbolic formula. Where operators are substituted by CENNs Data symbols are the inputs for tree leafs. The formula output is the tree root output.

12. Designing the CNNTree

13. Design constraints In this work we used the following design: Fixed tree structure. Full binary tree structure.

14. Design constraints (CONT.) In this work we used the following design: Single perceptron with two inputs as a CENN unified structure. CENN library contains CENNs for Boolean logic operators. The used operators in the CENNL are AND , OR , NOT1 , and NOT2 , where NOTi complements the ith input . In this work, additional CENN items are introduced, TRANSFERE1 and TRANSFERE2 which transfer the corresponding input directly to the output, without changing it .

15. Design constraints (CONT.) CNNTREE with depth: 3 layers Training set vectors x0 x1 x2 d0 … .. … . … . … . … .. … . … . … . … .. … . … . … . … .. … . … . … . … .. … . … . … . … .. … . … . … . … .. … . … . … . … .. … . … . … . … .. … . … . … .

16. Designing CNNTREE The design problem could be summarized in finding the following: CENNs from CENN library for each node in the CNNTREE. Input from problem inputs for each leaf node input. The configuration of CNNTREE nodes and inputs should minimize the error . To solve this problem, Design by Neural Networks methods are tried: Supervised Method Unsupervised Method A simple genetic algorithm (SGA) is adopted .

17. Design using Genetic Algorithms The used genetic algorithm has three operators : R oulette wheel selection O ne-point crossover Byte mutation The genotype of CNNTREE is the concatenation of : CENNs indices in the CENNs library A ssigned inputs indices Each index is represented by 8-bits binary number , where

18. Experiments & Results

19. Digits recognition An experiment of recognizing numerical character patterns is illustrated here Ten numerical character patterns are used [0-9] . Each pattern consists of 64 (8 x 8) pixels black and white.

20. Genetic Algorithm Parameters Mutation probability is 0.05 Crossover probability is 0.8 Population size is 20 chromosomes The genetic algorithm is programmed to stop when it finds a tree with fitness value more than 10

21. Correctness experiment An experiment is done on evolved CNNTREE so as to measure its correctness by generating random noisy pixels for the patterns. For every pattern, from 1 to 9 random pixels are selected and their values are inverted. At every number of noisy pixels, the experiment is done 100 times and the count of correctly classified patterns is measured. The experiment is performed for different CNNTREEs with depths from 7 to 9 layers . The same experiments are conducted using single hidden layer feed forward neural network so as to know how much these results are good.

22. Correctness results using CNNTREE Correctness ratio of CNNTREEs at error threshold 0.1, 0.2, 0.3, and 0.4

23. Correctness results using FF ANN Correctness ratio of feed forward neural network at different threshold values

24. Correctness results Feed-forward neural network CNNTREE

25. Performance experiments The number of generations and the generation times are measured when designing a CNNTREE using the proposed genetic algorithm. The average overall time for training the CNNTREE versus tree depth is plotted. Experiment for measuring the back-propagation time is done. The learning time of the patterns is measured, and the average time for learning a pattern is calculated and plotted. Both experiments are repeated 10 times for every tree depth from 6 to 10 layers .

26. Performance Results for designing CNNTREE Average total genetic training time versus CNNTREE depth, done on Intel Pentium 1.70 GHz processor.

27. Performance Results for on-line LOCAL training Average back-propagation training epoch time versus network tree depth

28. Supervised method Try to know the appropriate configuration for certain neural network using previously known configurations for other problems Unsupervised methods Use Train – Classify – Modify iterations until find suitable configuration Designing CNNTREEs using ANNs

29. Supervised method

30. Unsupervised method

31. Unsupervised method Training using Back Propagation Classification is based upon the Euclidian distance of Weights from primitives weights Outputs from primitives outputs Modification is based on selecting the most far N classified primitives and randomizing them, and this is the weak point of this approach.

32. CONCLUSION A new type of modular neural networks – comprehensible neural network tree (CNNTREE) – is introduced. Experimental results with a digit recognition problem show that CNNTREE generalization is comparable for single hidden layer feed forward neural networks generalization, while CNNTREE is constructed to be easily interpreted for symbolic systems .

33. Thank you for Your attention