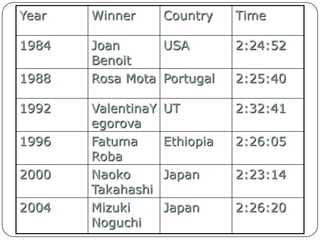
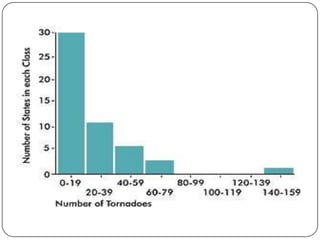
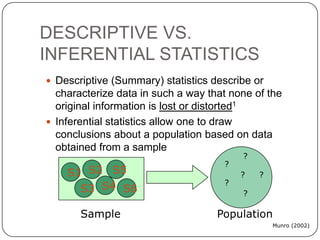
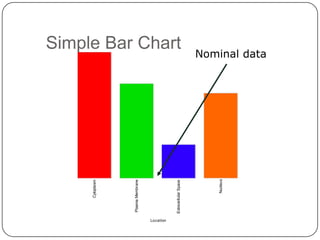
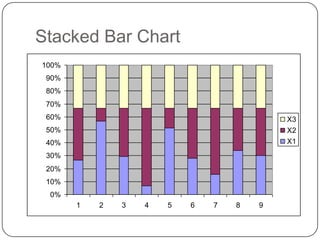
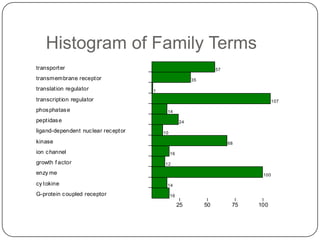
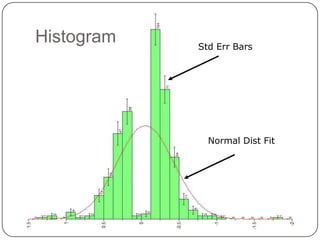
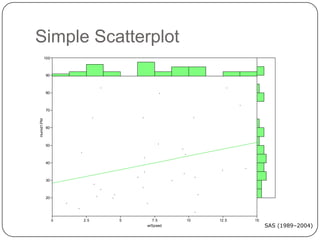
This document discusses quantitative data analysis and descriptive and inferential statistics. It provides the following key points: - Quantitative data is measured numerically along a scale and reported as scores or other numeric values. Descriptive statistics summarize and describe quantitative data. - Descriptive statistics include numerical summaries that measure central tendency and variability of data, as well as graphical summaries like histograms. They characterize data without generalizing beyond the sample. - Inferential statistics allow inferences about populations based on samples. Methods include hypothesis testing, regression, and principle components analysis. Hypothesis testing involves stating and evaluating null and alternative hypotheses using sample data and test statistics. - Descriptive statistics simply describe or characterize sample data, while inferential

1. NOR LAILATUL AZILAH HAMDZAH
2012132013
QUANTITATIVE DATA
ANALYSIS

2. 2 FUNDAMENTAL TYPES OF
NUMERICAL DATA
 To collect information such as
abilities, attitudes, beliefs, reactions and etc.
 It can be reported in 3 ways – words, numbers
and sometime through graphs or chart

3. QUANTITATIVE DATA
 Are obtained when the variable being studied is
measured along a scale that indicates how much
of the variable is present.
 Are reported in term of score
 E.g: the anxiety scores of all first-year students
enrolled at San Francisco University at 2002
(variable – anxiety)

4. 1.Descriptive statistics
 Descriptive statistics are numbers that
are used to summarize and describe
data (the information that has been
collected from an experiment, a
survey, an historical record, etc.).

5. 1.Descriptive statistics
Descriptive statistics is just
descriptive. It does not involve
generalizing beyond the data at
hand. Generalizing from our data to
another set of cases is the business
of inferential statistics.

6.  Allows one to examine each variable
separately to check for data
inconsistencies, variability of variables
 Also allows one to check statistical
assumptions about the shape of the
distribution before moving on to more
complex analysis
 Univariate descriptive statistics can also
be used to determine central
tendency, variability, skewness, and
1.Descriptive statistics

7. 1.Descriptive statistics
 It can include:
graphical summaries that show the
spread of the data; numerical
summaries that either measure the
central tendency (a 'typical' data value)
of a data set or describe the spread of
the data.

8. Example: numerical summary
 Descriptive statistics is central to the world of sports.
For the Olympic marathon (a foot race of 26.3
miles), we possess data that cover more than a
century of competition. (The first modern Olympics
took place in 1896). The following table shows the
winning times for women, who have only been
allowed to compete since 1984).

9. Year Winner Country Time
1984 Joan
Benoit
USA 2:24:52
1988 Rosa Mota Portugal 2:25:40
1992 ValentinaY
egorova
UT 2:32:41
1996 Fatuma
Roba
Ethiopia 2:26:05
2000 Naoko
Takahashi
Japan 2:23:14
2004 Mizuki
Noguchi
Japan 2:26:20

10. Example: graphical summary
 A kind of graphical summary is the
histogram, which combines data into groups or
classes as a way to generalize the details of a
data set while at the same time illustrate the
data's overall pattern.
 Let’s see an example.

12.  In the previous histogram we see that the first class
contains all the States that experienced between
zero and nineteen tornadoes during 2000.
 Histograms can show gaps where no data values
exist (the 100-119 class). In this one, there are three
empty classes: 80-99, 100-119, and 120-139.

13. 2.Inferential statistics
 Inferential statistics is used to make
inferences, predictions or comparisons from
our data to more general conditions.
 Are certain types of procedures that allow
researchers to make inferences about a
population based on findings from the sample.

14. 2.Inferential statistics
 On the contrary, with descriptive statistics we
condense a set of known numbers into a few
simple values (either numerically or
graphically) to simplify an understanding of
those data.
 Other examples of inferential statistics
methods include hypothesis testing, linear
regression, and principle components
analysis.

15. 2.1.Hypothesis testing
 Statistical hypothesis is an assumption about
a population parameter. This assumption may
or may not be true.
 The best way to determine whether a
statistical hypothesis is true would be to
examine the entire population. Since that is
often impractical, researchers typically
examine a random sample from the
population.

16. 2.1.Hypothesis testing
 There are two types of statistical hypotheses.
Null hypothesis (denoted by H0): the
hypothesis that sample observations result
purely from chance.
Alternative hypothesis (denoted by H1 or
Ha): the hypothesis that sample observations
are influenced by some non-random cause.

17. 2.1.Hypothesis testing
 Statisticians follow a formal process to determine
whether to accept or reject a null
hypothesis, based on sample data. This process
is called hypothesis testing.
 It consists of four steps:
1st step. State the hypotheses.
This involves stating the null and alternative
hypotheses. The hypotheses are stated in such a
way that they are mutually exclusive. That is, if
one is true, the other must be false.

18. 2.1Hypothesis testing
2nd step. Formulate an analysis plan. It
describes how to use sample data to accept
or reject the null hypothesis. The accept/reject
decision often focuses around a single test
statistic.
3rd step. Analyze sample data.
Find the value of the test statistic (mean
score, proportion, t-score, z-score, etc.)
described in the analysis plan. Complete other
computations, as required by the plan.

19. 2.1Hypothesis testing
4th step. Interpret results.
Apply the decision rule described in the analysis
plan. If the test statistic supports the null
hypothesis, accept the null hypothesis;
otherwise, reject the null hypothesis.

20. Hypothesis testing: example
 We wish to prove a new vaccine is more effective
than the current vaccine used for preventing a
particular disease. The null hypothesis is that
there is no difference in efficacy between the two
vaccines. The alternative hypothesis is that the
new vaccine is better.

21. Hypothesis testing: example
 We need a measurement that indicates the
efficacy of each vaccine. The difference
between the count of occurrences of the
disease for the old vaccine and the count of
occurrences of the disease for the new
vaccine is calculated. If it is sufficiently
large, the null hypothesis - that there is no
difference between in efficacy between the
two vaccines - is rejected. If the difference is
not sufficiently large, we fail to reject the null
hypothesis.

22. Hypothesis testing: example
 In all hypothesis testing, the final conclusion once
the test has been carried out is always given in
terms of the null hypothesis.

23. DESCRIPTIVE VS.
INFERENTIAL STATISTICS
 Descriptive (Summary) statistics describe or
characterize data in such a way that none of the
original information is lost or distorted1
 Inferential statistics allow one to draw
conclusions about a population based on data
obtained from a sample
Munro (2002)
S1 S2
S3 S4
S5
S6
?
??
?
?
?
Sample Population

24. Graphical Methods for Displaying
Data
 Frequency Distributions
 Histograms
 Plots
 Pareto Charts
 Boxplots
 Error Bar Charts

25. Cytoplasm
PlasmaMembrane
ExtracellularSpace
NucleusLocation
Simple Bar Chart Nominal data

26. Stacked Bar Chart
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
1 2 3 4 5 6 7 8 9
X3
X2
X1

27. G-protein coupled receptor
cy tokine
enzy me
growth f actor
ion channel
kinase
ligand-dependent nuclear receptor
peptidase
phosphatase
transcription regulator
translation regulator
transmembrane receptor
transporter
16
14
100
12
16
68
10
24
14
107
1
35
57
25 50 75 100
Histogram of Family Terms

28. Histogram Std Err Bars
Normal Dist Fit

29. Simple Scatterplot
20
30
40
50
60
70
80
90
100
Humid1:PM
0 2.5 5 7.5 10 12.5 15
wrSpeed SAS (1989–2004)

30. The End…. Any Question?