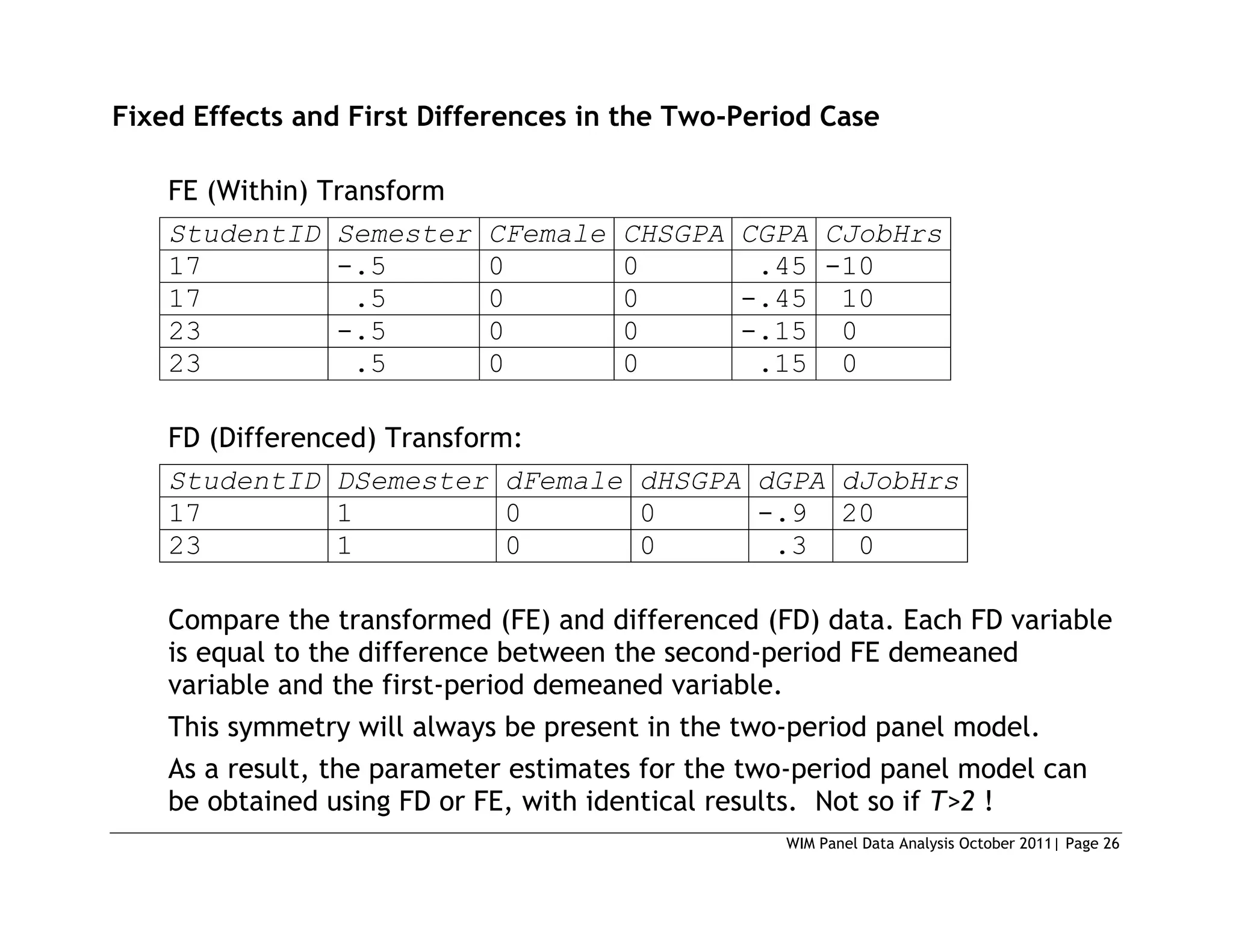
This document provides an introduction to panel data analysis and regression models for panel data. It defines panel data as longitudinal data collected on the same units (like individuals, firms, countries) over multiple time periods. Panel data allow researchers to study changes over time and estimate causal effects. The document outlines common panel data structures, reasons for using panel data analysis, and basic estimation techniques like fixed effects and random effects models to account for unobserved heterogeneity across units. It also discusses assumptions and limitations of different panel data models.




































= 30.25
Prob>chi2 = 0.0000
We reject the null and conclude the fixed effects estimator is appropriate.](https://image.slidesharecdn.com/panelslides-220318122543/75/Panel-slides-38-2048.jpg)
![WIM Panel Data Analysis October 2011| Page 38
Interpretation of Results from the Error Components Model
Since the UEM model is derived as a levels model, coefficients can be
interpreted much the same as interpretations of a conventional OLS
model, but there are nuances:
For example, suppose we estimate the relationship between marriage and
men’s wages, ˆ 0.05
MARRIED in every model.
Pooled OLS cross-section coefficients contain information about average
differences between units.
[ | ]
it it it i
E y c
x x
This is a population-averaged effect. On average, married men earn 5%
more than men who are not married.
This says nothing about the causal effect of marriage on men’s earnings.](https://image.slidesharecdn.com/panelslides-220318122543/75/Panel-slides-39-2048.jpg)
![WIM Panel Data Analysis October 2011| Page 39
RE/FE/FD estimate average effects within units.
If the unobserved effects are exogenous these are asymptotically
equivalent to the population averaged effect.
[ | , ]
it it i it
E y c
x x
This is sometimes called an average treatment effect. On average,
entering marriage increases men’s earnings by 5%.
RE coefficients represent average change within units, estimated from all
units whether they experience change or not.
FE and FD coefficients represent average changes within units, only for
units that did experience change
This is akin to a treatment effect among the treated. On average, men
who married increased their earnings by 5%.](https://image.slidesharecdn.com/panelslides-220318122543/75/Panel-slides-40-2048.jpg)

