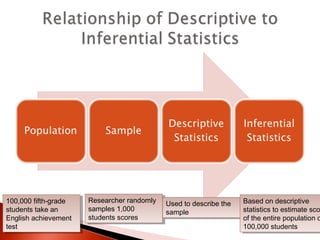
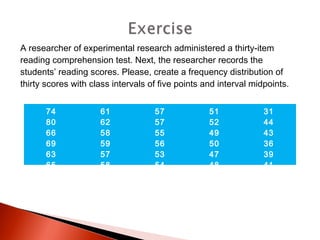
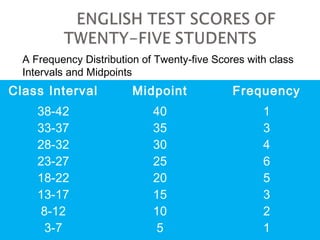
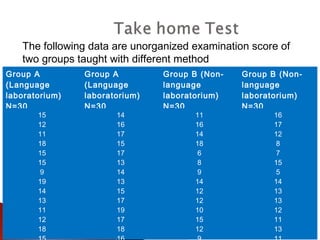
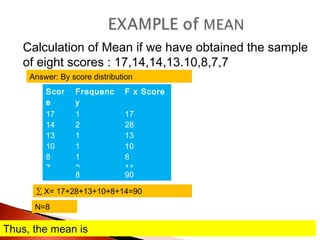
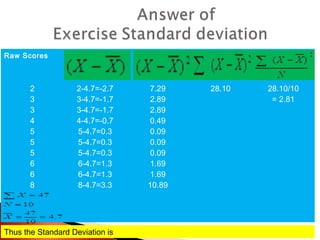
The document provides an overview of statistical methods, including descriptive and inferential statistics. Descriptive statistics summarize and organize data from specific samples, while inferential statistics draw conclusions about a population based on sample data. It also discusses the use of graphs, measures of central tendency, variance, and standard deviation in analyzing numerical data.

1. Thursday, October 9, 2014 1

2. Refers to methods and techniques
used for describing, organizing,
analyzing, and interpreting
numerical data.

3.  The field of statistics is often divided into two
broad categories : descriptive statistics and
inferential statistics.
 Descriptive statistics transform a set of numbers
or observations into indices that describe or
characterize the data.

4.  Thus, descriptive statistics are used to classify,
organize, and summarize numerical data about a
particular group of observations.
 There is no attempt to generalize these statistics,
which describe only one group, to other samples
or population.

5.  In other words, descriptive statistics are used to
summarize, organize, and reduce large numbers
of observations.
 Descriptive statistics portray and focus on what is
with respect to the sample data, for example:
1. What is the average reading grade level of the fifth
graders in the school?”
2. How many teachers found in-service valuable?”
3. What percentage of students want to go to
college?

6. Inferential statistics (sampling
statistics), involve selecting a sample
from a defined population and
studying that sample in order to draw
conclusions and make inferences
about the population.

7. 100,000 fifth-grade
students take an
English achievement
test
100,000 fifth-grade
students take an
English achievement
test
Researcher randomly
samples 1,000
students scores
Researcher randomly
samples 1,000
students scores
Used to describe the
sample
Used to describe the
sample
Based on descriptive
statistics to estimate scores
of the entire population of
100,000 students
Based on descriptive
statistics to estimate scores
of the entire population of
100,000 students

9. Focuses on ways to organize
numerical data and present them
visually with the use of graphs.
One way to organize your data is to
create a frequency distribution.
 Various software programs, such as
Excel, can easily produce graphs for
you.

10. Allows researchers and educators to
describe, summarize, and report their
data.
By organizing data, they can compare
distributions and observe patterns.

11. In most cases, the original data we
collect is not ordered or summarized.
 Therefore, after collecting data, we
may want to create a frequency
distribution by ordering and tallying
the scores.

12. A seventh-grade social studies teacher wants to assign
end-of term letter grades to the twenty-five students in
her class.
After administering a thirty-item final examination, the
teacher records the students’ test scores.

13. 27
25
30
24
19
16
28
24
17
21
23
26
29
23
18
22
20
17
24
23
21
22
28
26
25
These scores show the number of correct answers
obtained by each students on the social studies final
examination.
Next, the researcher can create a frequency
distribution by ordering and tallying these scores.

14. Score Frequency Score Frequency
30
29
28
27
26
25
24
23
11212233
22
21
20
19
18
17
16
2211121

15.  The researcher/teacher may want to group every
scores together into class interval to assign letter
grade to the students.
Class interval
(5 points)
Mid point Frequency
26-30
21-25
16-20
28
23
18
7
12
6
Σ 25

16. A researcher of experimental research administered a thirty-item
reading comprehension test. Next, the researcher records the
students’ reading scores. Please, create a frequency distribution of
thirty scores with class intervals of five points and interval midpoints.
74
80
66
69
63
65
61
62
58
59
57
58
57
57
55
56
53
54
51
52
49
50
47
48
31
44
43
36
39
41

17. Graphs are usually to communicate
information by transforming numerical
data into a visual form.
Graphs allow us to see relationships not
easily apparent by looking at the
numerical data.
There are various forms of graphs, each
are appropriate for a different type of data.

18. In drawing histogram and frequency
polygon, the vertical axis always
represents frequencies, and the
horizontal axis always represents scores
or Class interval (Mid point).
The lower values of both vertical and
horizontal axes are recorded at the
intersection of the axes (at the bottom left
side).

19. Lowest Highest
Highest
Lowest

20. Frequency distribution in the following table can be
depicted using two types of graphs, a histogram or a
frequency polygon.
Score Frequency
654321
124321

21. A Frequency Distribution of Twenty-five Scores with class
Intervals and Midpoints
Class Interval Midpoint Frequency
38-42
33-37
28-32
23-27
18-22
13-17
8-12
3-7
40
35
30
25
20
15
10
5
13465321

22. The following data are unorganized examination score of
two groups taught with different method
Group A
(Language
laboratorium)
N=30
Group A
(Language
laboratorium)
N=30
Group B (Non-language
laboratorium)
N=30
Group B (Non-language
laboratorium)
N=30
15
12
11
18
15
15
9
19
14
13
11
12
18
15
14
16
17
15
17
13
14
13
15
17
19
17
18
16
11
16
14
18
689
14
12
12
10
15
12
9
16
17
12
87
15
5
14
13
13
12
11
13
11

23. The following data are unorganized examination score of
two groups taught with different method
a. Arrange the frequency distribution of scores!
b. Arrange interval frequency distribution of scores of five
points!
c. Figure the histogram of the scores!
d. Figure the frequency Polygon of the scores!
e. Take a conclusion from the histogram and frequency
polygon you graph.

26. They are descriptive statistics that measure the
central location or value of sets of scores.
A measure of central tendency is a summary
score that is used to represent a distribution of
scores.
It is a summary score that represents a set of
scores.
They are used widely to summarize and
simplify large quantities of data.

27. The mode of the distribution is the score that
occurs with the greatest frequency in that
distribution.
Score Frequency
Mode
12
11
10
98765 11234211
We can see that the score of 8 is repeated the most (four times);
therefore, the mode of the distribution is 8.

28. The mode of the distribution is the score that
occurs with the greatest frequency in that
distribution.
Score Frequency
Mode
12
11
10
98765
11234211
We can see that the score of 8 is repeated the most (four
times); therefore, the mode of the distribution is 8.

29. The mode in the distribution below is?
Score Score
16
22
17
22
18
22
18
23
20
We can see that the score of 22 is repeated the most (three
times); therefore, the mode of the distribution is 22.

30.  The median is the middle point of a distribution
of scores that are ordered
 Fifty percent of the scores are above the median
, and 50 percent are below it.
Score
Median
10
876421
The score 6 is the median because there are three scores
above it and three below it.

31.  If the distribution has an even number of scores,
the median is the average of the two middle
scores.
Score
20
16
12
10
Median Two middle scores
877642
Thus, the median in the score above is (7+8):2= 7.5

32.  It is the “arithmetic average” of a set of scores.
 It is obtained by adding up the scores and
dividing that sum by the number of scores.
 The statistical symbol for the mean of a sample
is χ (pronounced “ex bar”).
 A raw score is represented in statistics by the
letter X.
 A raw score is score as it was obtained on a test
or any other measure, without converting it to
any other scale.

33.  The statistical symbol for the population mean is
μ, the Greek letter mu (pronounced “moo” or
“mew”).
 The statistical symbol for “sum of” is Σ (the
capital Greek letter sigma).
 The formula for calculating the mean is
or

34.  The statistical symbol for the population mean is
μ, the Greek letter mu (pronounced “moo” or
“mew”).
 The statistical symbol for “sum of” is Σ (the
capital Greek letter sigma).

35. Calculation of Mean if we have obtained the sample
of eight scores : 17,14,14,13.10,8,7,7
Answer: By using raw score
Score Score
17
10
14
14
13
877 Σ X= 17+14+14+13+10+8+7+7=90
N=8
Thus, the mean is

36. Calculation of Mean if we have obtained the sample
of eight scores : 17,14,14,13.10,8,7,7
Answer: By score distribution
Scor
e
Frequenc
y
F x Score
17
14
13
10
87
121112
17
28
13
10
8
14
8 90
Σ X= 17+28+13+10+8+14=90
N=8
Thus, the mean is

38. Are used to show the differences among
the scores in a distribution.
We use the term variability or dispersion
because the statistics provide an
indication of how different, or dispersed,
the scores are from one another.

39. The range is the simplest; but also least
useful, measure of variability.
It is defined as the distance between the
smallest and the largest scores.
It is calculated by simply subtracting the
bottom, or lowest, score from the top, or
highest score.
Range = XH- XL
XH = the highest score
XL = the lowest score

40. Determine the range and the mean from the
following sets of figures :
a. 1,4,9,11,15,19,24,29,34
b. 14,15,15,16,16,16,18,18,18
Answer a: Mean= ........ Range ...........
Answer b: Mean= ........ Range .........

41. The distance between each score in a
distribution and the mean of that
distribution is called the deviation
score.
The mean of the deviation scores is called
the standard deviation (SD)
The standard deviation tells you” how
close the scores are to the mean.”

42. The SD describes the mean distance of
the scores around the distribution mean.
Squaring the SD give us another index of
variability, called the VARIANCE.
The Variance is needed in order to
calculate the SD (Standard Deviation).

43. If the standard deviation is a small
numbers, this tells you that the scores are
“bunched together” close to the mean.
 If the standard deviation is a large
number, this tells you that the scores are
“spread out” a greater distance from the
mean.

44. The formula for standard deviation is:
for group scores

45. The variance (S2) is a measure of dispersion
that indicates the degree to which scores
cluster around the mean.
Computationally, the variance is the sum of the
squared deviation scores about the mean
divided by the total number of scores/the total
number of scores minus one.
or

46. or
 If we have only five scores. It is very likely that such a small
group of scores is a sample, rather than a population. Therefore,
we computed the variance and SD for these scores, treating
them as a sample, and used a denominator of N-1 in the
computation.
When, on the other hand, we consider a set of scores to be a
population, we should use a denominator of N to compute the
variance.

47. For any distribution of scores, the variance
can be determined by following five steps:
Step 1:calculate the mean: (ΣX/N)
Step 2: calculate the deviation scores:
Step 3: Square each deviation score :
Step 4: Sum all the deviation scores:
Step 5 : Divide the sum by N:

48. Calculate the standard deviation from the following
scores: 2,3,3,4,5,5,5,6,6,8
Answer: Calculate the variance by using 5 steps
Step 1:calculate the mean: (ΣX/N)
Step 2: calculate the deviation scores:
Step 3: Square each deviation score :
Step 4: Sum all the deviation scores:
Step 5 : Divide the sum by N:

49. Raw Scores
2334555668
2-4.7=-2.7
3-4.7=-1.7
3-4.7=-1.7
4-4.7=-0.7
5-4.7=0.3
5-4.7=0.3
5-4.7=0.3
6-4.7=1.3
6-4.7=1.3
8-4.7=3.3
7.29
2.89
2.89
0.49
0.09
0.09
0.09
1.69
1.69
10.89
28.10 28.10/10
= 2.81
Thus the Standard Deviation is

50. Calculate the standard deviation from the following
scores: 20,15,15,14,14,14,12,10,8,8
Answer: Calculate the variance by using 5 steps
Step 1:calculate the mean: (ΣX/N)
Step 2: calculate the deviation scores:
Step 3: Square each deviation score :
Step 4: Sum all the deviation scores:
Step 5 : Divide the sum by N: