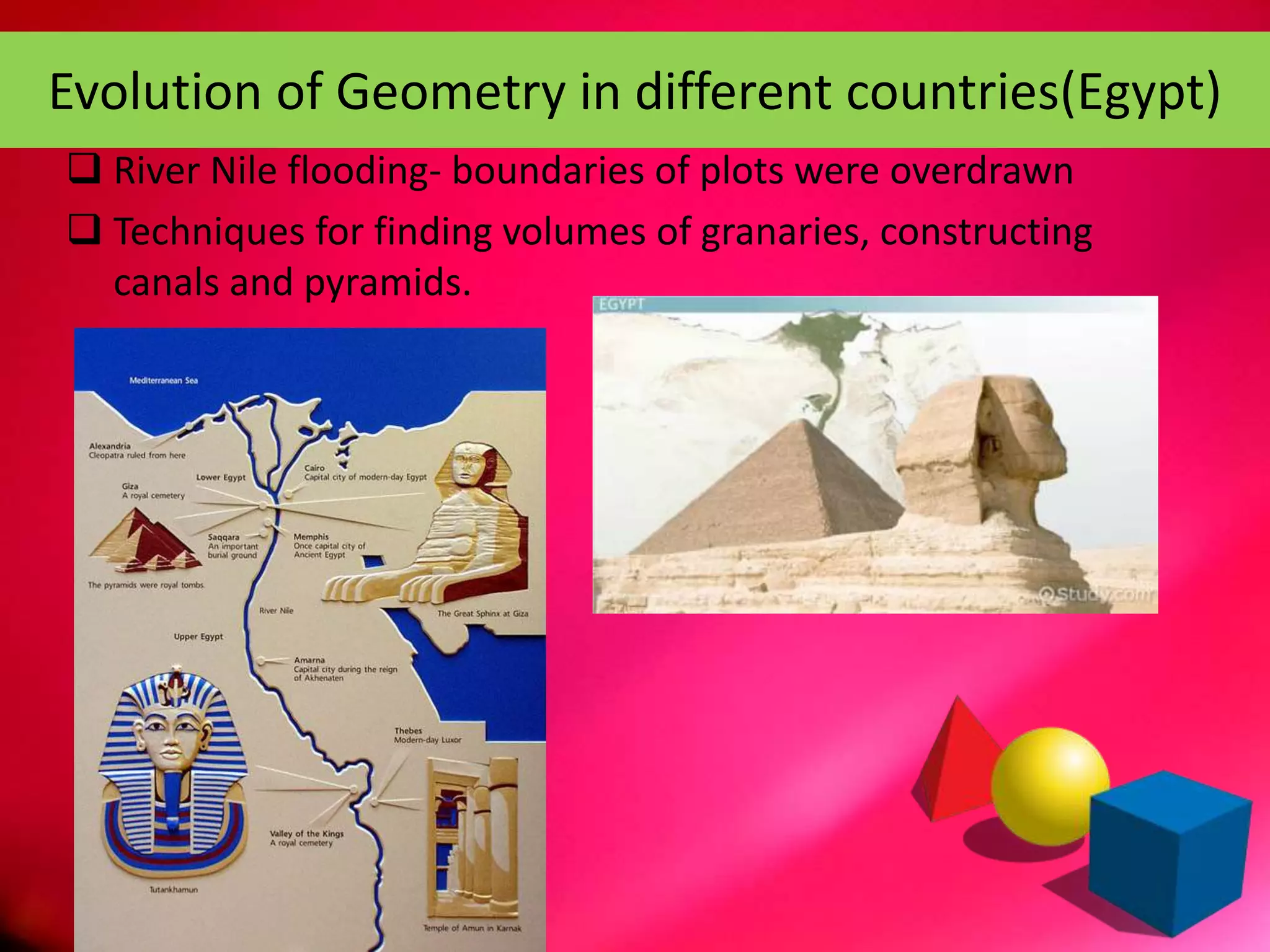
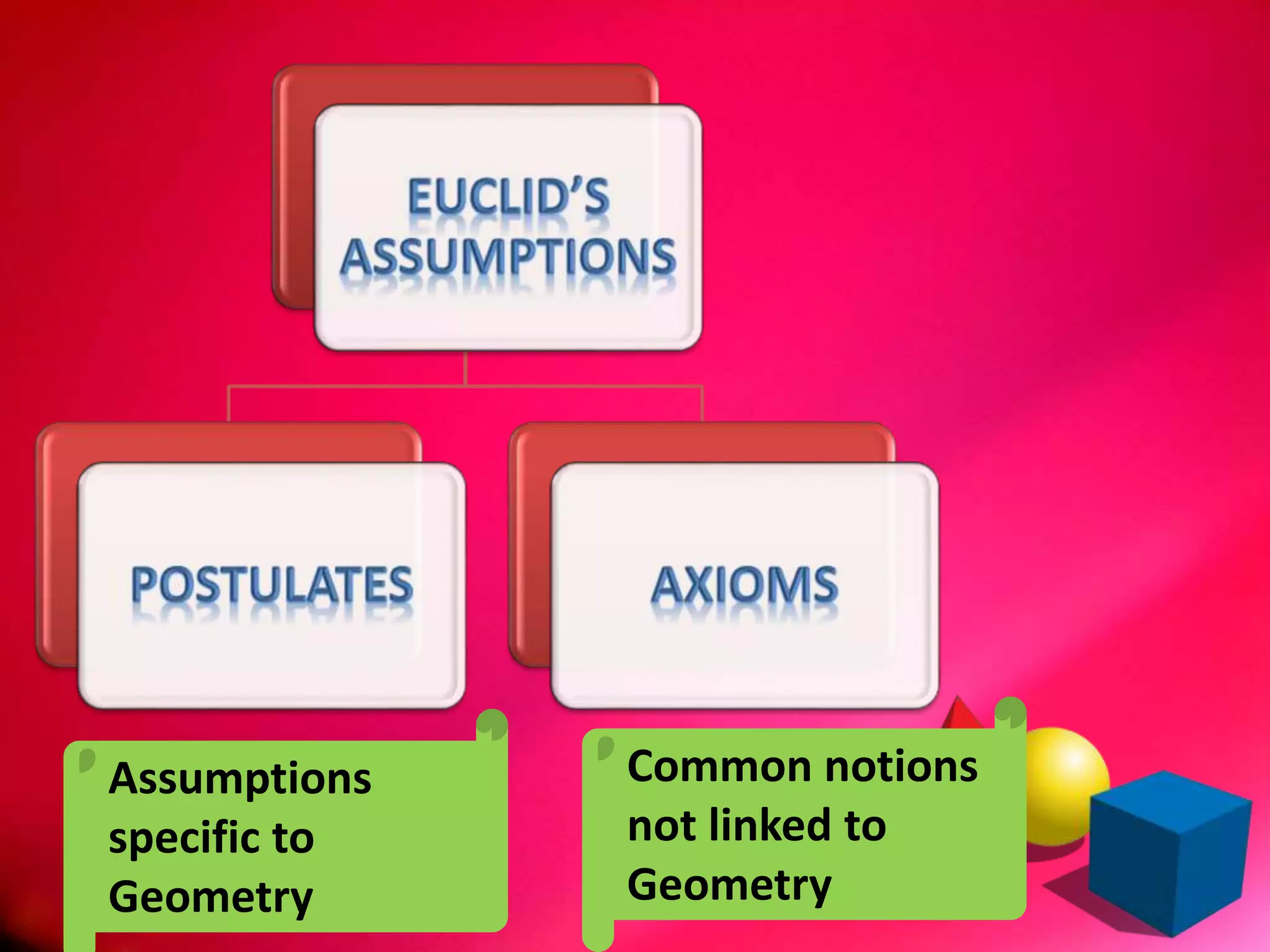
This document discusses the history and evolution of geometry. It begins by defining geometry as the measurement of earth and outlines its origins in ancient Egypt and the Indus Valley civilization where it was used to measure land and construct buildings. It then covers important early Greek mathematicians like Thales and Pythagoras and their theorems. Most of the document focuses on Euclid's Elements, outlining his definitions, postulates, axioms and use of deductive reasoning to prove 465 theorems. It also discusses criticisms of Euclid's definitions and the development of non-Euclidean geometry on curved surfaces.

1. By
Ms.Arshi

2. Introduction
Geometry:-’Geo’ means “earth” and ‘metrein’
means “to measure”.
Need of measuring land

3. Evolution of Geometry in different countries(Egypt)
 River Nile flooding- boundaries of plots were overdrawn
 Techniques for finding volumes of granaries, constructing
canals and pyramids.

4.  Truncated Pyramid -Volume

5. Use of Geometry in Indus Valley Civilization
Excavations at Harappa and Mohenjodaro.
Cities , roads, drainage systems, rooms of
different types(mensuration and practical
arithmetic), bricks (4:2:1)

6. Geometry was in

7. Thales (Greek Mathematician)
 Thales gave first known proof
 Circle is bisected by its
diameter

8.  Pythagoras Theorem
Pythagoras

9. Euclid
(325-265 BC)
“Elements”
Treatise on
Math &
Geometry

10. Euclid’s Definitions
1. A point is that which has no part.
2. A line is breadthless length.
3. The ends of a line are points.
4. A straight line is a line which lies evenly with the
points on itself.
5. A surface is that which has length and breadth
only.
6. The edges of a surface are lines.
7. A plane surface is a surface which lies evenly with
the straight lines on itself.

11.  The definitions of a point, a line, and a plane, are not accepted
by mathematicians. Therefore, these terms are taken as
undefined.
 Models
Euclid’s Definitions problem

12. Assumptions
specific to
Geometry
Common notions
not linked to
Geometry

13. Euclid's Postulates:
1. A straight line can be drawn from any point to any point.
2. A terminated line can be produced indefinitely.
3. It is possible to describe a circle with any centre any
distance.
4. All right angles are equal to one another.
5. If a straight line falling on two straight lines makes the
interior angles on the same side of it taken together less
than two right angles, then the two straight lines, if
produced indefinitely, meet on that side on which the sum
of angles is less than two right angles.

14. Two equivalent versions of the Fifth
Euclid’s postulates:
(i). ‘For every line l and for every point P not
lying on l, there exists a unique line m passing
through P and parallel to l’.
(ii). Two distinct intersecting lines cannot be
parallel to the same line.

15. Euclid's Axioms:
1. Things which are equal to the same things are also equal to one
another.
E.g. If A=B & C=B. that is both A & C are equal to B, then A & C will be equal.
2. If equals are added to equals, then the wholes are equal.
E.g. Two glasses A & A’ has same volume of water. Now we add equal quantity of
water B, to both glass A & A’, then the final volume of water in the jar will be
same. A+ B will be equal to A’ + B.
3. If equals are subtracted from equals, then the remainders are
equal.
E.g. Two glasses A & A’ has same volume of water. Now we remove equal quantity of
water B, from both glass A & A’, then the final volume of water in the jar will be
same. A- B will be equal to A’ - B.
4. Things which coincide with one another are equal to one
another.
E.g. if two triangles coincide with each other then they are equal.

16. Euclid's Axioms:
5. The whole is greater than the part.
This statement is true in physics, chemistry, mathematics, geometry, biology,
economics etc.
6. Things which are double of the same things are equal to one
another.
If A= A’ then 2A= 2A’.
7. Things which are halves of the same things are equal to one
another.
If A= A’ then ½ A= ½ A’.

17. Theorems or Prepositions:
After stating Postulates & Axioms, Euclid used
these to prove other results by applying
deductive reasoning.
E.g.: “Diameter divides circle in 2 parts” is a
theorem. Euclid deduced 465 Theorems.
“Two distinct lines cannot have more than one
point in common” is a theorem.

18. Non Euclidean Geometry/Spherical geometry
Lines are not straight.
They are parts of great circles (i.e., circles obtained by the
intersection of a sphere and planes passing through the
centre of the sphere).
 5th postulate of Euclid-
Lines AN & BN should not meet
but they meet at point N.
It has been proved that Euclidean geometry is valid only
for the figures in the plane. On the curved surfaces, it fails.