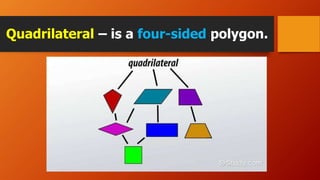
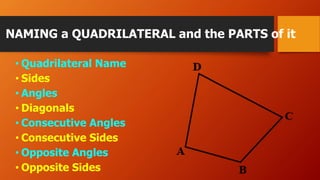
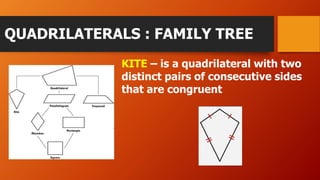
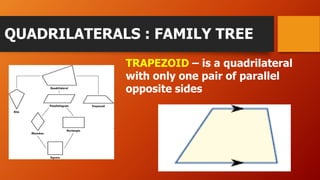
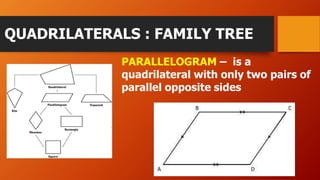
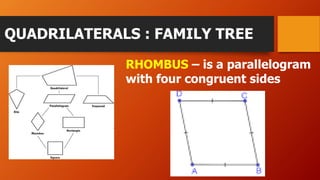
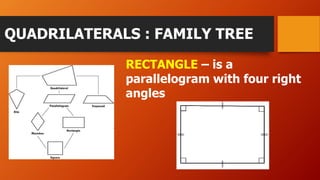
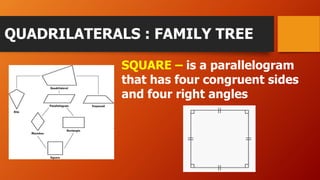
This document discusses different types of quadrilaterals including their definitions and properties. It defines a quadrilateral as a four-sided polygon and introduces various terms used to describe quadrilateral parts such as sides, angles, and diagonals. It then presents different types of quadrilaterals in a family tree showing their relationships and provides detailed definitions and properties for parallelograms, rhombuses, rectangles, and squares. The document concludes with an example problem involving finding measurements of a parallelogram using its properties.

1. 2nd QUARTER:
QUADRILATERALS

2. Quadrilateral – is a four-sided polygon.

3. NAMING a QUADRILATERAL and the PARTS of it
• Quadrilateral Name
• Sides
• Angles
• Diagonals
• Consecutive Angles
• Consecutive Sides
• Opposite Angles
• Opposite Sides

4. NAMING a QUADRILATERAL and the PARTS of it
• Quadrilateral Name
• Sides
• Angles
• Diagonals
• Consecutive Angles
• Consecutive Sides
• Opposite Angles
• Opposite Sides

5. QUADRILATERALS : FAMILY TREE

6. QUADRILATERALS : FAMILY TREE
KITE – is a quadrilateral with two
distinct pairs of consecutive sides
that are congruent

7. QUADRILATERALS : FAMILY TREE
TRAPEZOID – is a quadrilateral
with only one pair of parallel
opposite sides

8. QUADRILATERALS : FAMILY TREE
PARALLELOGRAM – is a
quadrilateral with only two pairs of
parallel opposite sides

9. QUADRILATERALS : FAMILY TREE
RHOMBUS – is a parallelogram
with four congruent sides

10. QUADRILATERALS : FAMILY TREE
RECTANGLE – is a
parallelogram with four right
angles

11. QUADRILATERALS : FAMILY TREE
SQUARE – is a parallelogram
that has four congruent sides
and four right angles

12. QUADRILATERALS : FAMILY TREE
1. A rectangle is a parallelogram.
2. A square is a rhombus.
3. A square is a parallelogram.
4. A square is a quadrilateral.
5. A rhombus is a square.
6. A rectangle is a square.
7. A trapezoid is a quadrilateral.
8. A kite is a trapezoid.
9. A square is a rectangle.
10. A trapezoid is a parallelogram.

13. PARALLELOGRAM
A parallelogram is a quadrilateral that has two pairs of
opposite sides that are parallel.
PROPERTIES:
1. Opposite sides are congruent (≅).
2. Opposite angles are congruent.
3. Consecutive angles are
supplementary.
4. Diagonals bisect each other.

14. RHOMBUS
A rhombus is a parallelogram that has four congruent
sides.
PROPERTIES:
1. All properties inherited from the
parallelogram.
2. Diagonals are perpendicular (⊥).
3. Each diagonal bisects the angles of a
rhombus.

15. RECTANGLE
A rectangle is a parallelogram that has four right
angles.
PROPERTIES:
1. All properties inherited from the
parallelogram.
2. Diagonals are congruent.

16. SQUARE
A square is a parallelogram that has four congruent
sides and four right angles.
PROPERTIES:
1. All properties inherited from the
parallelogram.
2. All properties of rhombus.
3. All properties of a rectangle

17. Example:
A. Find the measures of the indicated parts
of parallelogram ABCD with diagonals
intersecting at point O using the properties
of a parallelogram.
1. AB =
2. BC =
3. OC =
4. DO =
5. 𝒎∠𝑫𝑨𝑩 =
6. 𝒎∠ABC =
7. Perimeter of parallelogram ABCD =