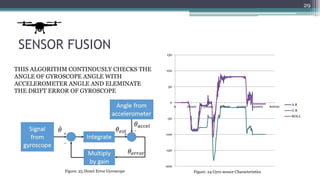
This document summarizes the implementation of a quadcopter with live video monitoring. It discusses the structure of the quadcopter, including its mechanical and electronic components. It also describes the SolidWorks design, MATLAB simulation, control theory using PID controllers, and sensor fusion techniques. The goal is to develop a stable quadcopter that can be flown wirelessly from a distance while transmitting live video footage. Future work may focus on more complex autonomous flight routines and swarm coordination.

1. IMPLEMENTATION OF QUADCOPTER WITH
LIVE MONITORING
Group Members:
AHMAD RAZA B126159
ASIF ALTAF B126151
MOHAMMAD SALEH B126156
HAFIZ ASADULLAH BAIG B126155
Supervisor:
Engr. M. Moid Sandhu

2. Overview
• Introduction
• Structure of quadcopter
• Design of quadcopter
• SolidWorks Design and MATLAB Simulation
• Architecture
• Video Transmitter/Receiver
• Control theory
• Sensor fusion
• PID controller
• Future development and implementation
• Conclusions
2

3. Introduction
• “To fly” has been one of the dreams of the humans
• But the story tells that building flying machines is not easy!
• A basic and common component: the wing
• Two kind of “flying machines” (excluding rockets and balloons):
▫ Fixed wing, i.e., airplanes
▫ Rotating wing, i.e., helicopters
3

4. Why Multi-rotors ...
• Are mechanically simple: they have n motors and n propellers
• Do not require complex mechanical parts to control the flight
• Can fly and move only by changing motor speed
• Are controlled only by a electronic-/computer-based system
Figure. 1 AR. Drone Figure. 2 DJI Phantom
4

5. Structure of quadcopter
• Mechanical :- A frame, 4 brushless motors (with frame pads and propeller
adapter), 4 rotors (two clockwise two counter clockwise), 4 esc, Screw pack
and instruments.
• Electronics :-A control board, battery, and radio receiver and some sensor
(gyroscope, accelerometer, barometer, pressure measurement) or IMU
(inertial measurement unit).
Figure. 3 Quadcopter Structure
5

6. Design of quadcopter
• Four equal propellers generating four thrust forces
• Two possible configurations: “+” and “× ”
• Propellers 1 and 3 rotates CW, 2 and 4 rotates CCW
• Required to compensate the action/reaction effect (Third Newton’s Law)
• Propellers 1 and 3 have opposite pitch w.r.t. 2 and 4, so all thrusts have the
same direction
Figure. 4 Frame Design
6

7. DYNAMICS(FORCES AND ROTATION SPEED)
• ω1 , ω2, ω3, ω4: rotation speeds of the propellers
• T1 , T2, T3, T4: forces generated by the propellers
• Ti ∝ ωi2: on the basis of propeller shape, air density, etc.
• mg: weight of the Quadrotor
• M1 , M2, M3, M4:
moments generated by the forces
Mi = L × Ti
• PITCH= θ
• ROLL= φ
• YAW= ψ
Figure. 5 Dynamics of Quadcopter
7

8. SolidWorks Design
Figure. 6 SolidWorks Design Frame
8

9. 3D EXPERIENCE Platform
Figure. 7 3D Platform
9

10. MATLAB Simulink
Figure. 8 Simulink MATLAB
10

11. 11

12. Figure. 9 Manually Tuned Gain of Angular Velocity
12
RESULTS AND ANALYSIS

13. Figure. 10 Automatic Tuned Gain of Angular Velocity
13

14. Figure. 11 Angular Displacement Manual Tuning
14

15. Figure. 12 Angular Displacement Automatic Tuning
15

16. HOVERING CONDITION
• 1 Equilibrium of forces: ∑4
i=1 Ti = −mg(Violating gives thrust)
• 2 Equilibrium of directions: T1 ,2,3,4 ||g
• 3 Equilibrium of moments: ∑4
i=1 Mi = 0
• 4 Equilibrium of rotation speeds: (ω1 + ω3) − (ω2 + ω4) = 0
(Violating gives Yaw)
• Violating one (or more) of these conditions implies to impose a certain
movement to the Quadrotor
• As a consequence:
φ = 0 θ = 0 ψ = 0
16

17. Architecture
User
PC
(ground station)
Transceiver
Base Station
Transceiver
Camera
(wireless)
Motors
Gyroscopes
Accelerometers
Magnetometer
Pressure
Sensor
Quadrotor
Attitude
PID
Angle
Estimate
Correction
Translation
PID
Reference
Microcontroller
Figure. 13 Architecture of Quadcopter
17

18. SCHEMATIC
Figure. 14 Schematic Diagram
18

19. Figure. 15 Video Transmitter/Receiver
19

20. CONTROL THEORY
Figure. 16 Control System
20

21. CONTROL THEORY
Same PWM signals applied different driver/motor/propeller
chains provoke different thrust forces, even if the components
are of the same type!
Solution!!!! Use feedback!
1 Measure your variable through a sensor
2 Compare the measured value with your desired set point
3 Apply the correction to the system on the basis of the error
4 Go to 1
Figure. 17 Motor Control
21

22. CONTROL THEORY
• In our scenario
▫ Our measures
 Actual angular velocities on the three axis (φ, θ, ψ)
 They are measured through a 3-axis gyroscope!, accelerometer and
magnetometer
▫ Our set points
 Desired angular velocities on the three axis (φ˙T, θ˙T, ψ˙T)
 They are given through the remote control
22

23. CONTROL THEORY
Figure. 18 Controller Firmware
23

24. FEEDBACK CONTROLLER-(P.I.D. CONTROLLER)
• The most common used controller type is the Proportional-
Integral-Derivative controller
▫ WHY PID?
 THE ANSWER IS WHY NOT
 If we only feed the error overcoming thrust value into controller its inertia
will overcompensate the error and new error will be generated and
quadcopter will remain oscillating continuosly.
 To reduce this error we should apply a controller which resist the change
while overcompensating which is perfectly done by derivative control
 And the oscillation is damped by integrating control.
24

25. PID CONTROLLER
• PID control is shown in block diagram form in Figure and is
performed in the following steps:
 The error e(t) is calculated as Set point – Measured State
 The proportional term P is calculated as [Kp * e(t)]
 The integral term I is calculated as [KI * 𝑡=0
𝑡=𝑛
e(t)]
 The derivative term D is calculated a [KD * (e(t) −e(t))] where e(t) is
previous error value
 The 3 terms are summed to produce the controller output, u(t) = P + I + D
• In order to stabilize the quadcopter, a separate PID controller was
implemented for the roll, pitch, and yaw axes.
25

26. PID CONTROLLER
Figure. 19 PID Controller
26

27. SENSOR FUSION (WHY?)
• Accelerometer gives us an absolute measurement of the
quadcopter orientation, but accelerometers are very prone to
noise. The motors on the quadcopter produce a lot of vibration,
introducing significant noise into the accelerometer reading.
• The gyroscope is much less effected by vibration, but it only gives
us angular rotation rates.
• By integrating the gyroscope readings, it is possible to estimate
the orientation , but this reading is prone to drifting over time.
27

28. SENSOR FUSION(COMPARISON)
-100
-50
0
50
100
0 10000 20000 30000 40000 50000 60000
ACCELEROMETER
-200
-150
-100
-50
0
50
0 10000 20000 30000 40000 50000 60000
GYROSCOPE
-150
-100
-50
0
50
100
0 20000 40000 60000
REAL ANGLE
Figure. 20 Accelerometer Figure.21 Gyroscope Figure. 22 Real Angle
28

29. SENSOR FUSION
-200
-150
-100
-50
0
50
100
150
0 10000 20000 30000 40000 50000 60000
A R
G R
ROLL
THIS ALGORITHM CONTINOUSLY CHECKS THE
ANGLE OF GYROSCOPE ANGLE WITH
ACCELEROMETER ANGLE AND ELEMINATE
THE DRIFT ERROR OF GYROSCOPE
Figure. 23 Direct Error Gyroscope Figure. 24 Gyro sensor Characteristics
29

30. Future development and implementation
• Quadcopters are a useful tool for university researchers to test and
evaluate new ideas in a number of different fields, including flight
control theory, navigation, real time systems, and robotics.
• In recent years many universities have shown quadcopters
performing increasingly complex aerial manoeuvres.
• Swarms of quadcopters can hover in mid-air fly in formations and
autonomously perform complex flying routines such as flips,
darting through hula hoops and organizing themselves to fly
through windows as a group.
30

31. Conclusion
• Although we built a working quadcopter, there is much room for
many improvements. First of all, we can make it much more stable
so that we could let it fly freely in an open place even with
spectators around.
• We can improve the accuracy of our wireless protocol to make it
possible to fly the quadcopter wirelessly from quite a distance.
31

32. References
• [1] RC Helicopter Fun, 2008. Understanding The RC
Quadrocopter / Multi rotor. Retrieved 12th October, 2013.
• [2] Andrew Gibiansky, 2012. Quadcopter Dynamics, Simulation,
and Control. Retrieved 12th October 2013.
• [3] Quadrotors.net, 2012. Why Quadrotors are so Popular for
Research? Retrieved 19th October 2013.
• [4] Czech Technical University, 2011. AR-Drone as a platform for
Robotic Research and education. Prague. Retrieved 19th October
2013.
• [5] IEEE Spectrum, 2011. Pendulum balancing Quadrocopter
learns some new tricks. Retrieved 19th October 2013.
32

33. 33