Introduction to Regression . pptx

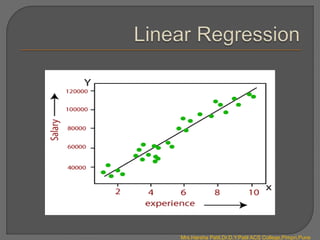
Mrs.Harsha Patil,Dr.D.Y.Patil ACS College,Pimpri,Pune

What is Regression :
 Regression analysis is a statistical method to model the relationship
between a dependent (target) and independent (predictor) variables with
one or more independent variables.
 It helps to understand how the value of the dependent variable is changing
corresponding to an independent variable when other independent variables
are held fixed. It predicts continuous/real values such as temperature.
 Regression is a supervised learning technique which helps in finding the
correlation between variables and enables us to predict the continuous
output variable based on the one or more predictor variables. It is mainly
used for prediction, forecasting, time series modeling, and determining
the causal-effect relationship between variables., age, salary, price, etc.

 In Regression, we plot a graph between the variables which best fits the
given data points, using this plot, the machine learning model can make
predictions about the data. In simple words, "Regression shows a line or
curve that passes through all the data points on target-predictor graph
in such a way that the vertical distance between the data points and
the regression line is minimum." The distance between data points and
line tells whether a model has captured a strong relationship or not.
 Some examples of regression can be as:
 Prediction of rain using temperature and other factors
 Determining Market trends
 Prediction of road accidents due to rash driving.

 Terminologies Related to the Regression :
 Dependent Variable: The main factor in Regression analysis which we want to
predict or understand is called the dependent variable. It is also called target
variable.
 Independent Variable: The factors which affect the dependent variables or which are
used to predict the values of the dependent variables are called independent variable,
also called as a predictor.
 Outliers: Outlier is an observation which contains either very low value or very high
value in comparison to other observed values. An outlier may hamper the result, so it
should be avoided.
 Multicollinearity: If the independent variables are highly correlated with each other
than other variables, then such condition is called Multicollinearity. It should not be
present in the dataset, because it creates problem while ranking the most affecting
variable.
 Underfitting and Overfitting: If our algorithm works well with the training dataset but
not well with test dataset, then such problem is called Overfitting. And if our algorithm
does not perform well even with training dataset, then such problem is
called underfitting.

 Types of Regression :
There are various types of regressions which are used in data science and
machine learning.
 Linear Regression
 Logistic Regression
 Polynomial Regression
 Support Vector Regression
 Decision Tree Regression
 Random Forest Regression
 Ridge Regression
 Lasso Regression:

Linear Regression:
 Linear regression is a statistical regression method which is used for
predictive analysis.
 It is one of the very simple and easy algorithms which works on regression
and shows the relationship between the continuous variables.
 It is used for solving the regression problem in machine learning.
 Linear regression shows the linear relationship between the independent
variable (X-axis) and the dependent variable (Y-axis), hence called linear
regression.
 If there is only one input variable (x), then such linear regression is
called simple linear regression. And if there is more than one input
variable, then such linear regression is called multiple linear regression.
 The relationship between variables in the linear regression model can be
explained using the below image. Here we are predicting the salary of an
employee on the basis of the year of experience.

 Some popular applications of linear regression are:
 Analyzing trends and sales estimates
 Salary forecasting
 Real estate prediction
 Arriving at ETAs in traffic.
1.Simple Linear Regression :
 Simple Linear Regression is a type of Regression algorithms that models the
relationship between a dependent variable and a single independent variable.
The relationship shown by a Simple Linear Regression model is linear or a
sloped straight line, hence it is called Simple Linear Regression.
 The key point in Simple Linear Regression is that the dependent variable must
be a continuous/real value. However, the independent variable can be
measured on continuous or categorical values.
 Simple Linear regression algorithm has mainly two objectives:

 Model the relationship between the two variables. Such as the
relationship between Income and expenditure, experience and Salary, etc.
 Forecasting new observations. Such as Weather forecasting according to
temperature, Revenue of a company according to the investments in a year,
etc.
 Recall the geometry lesson from high school. What is the equation of a line?
y = mx + c
Linear regression is nothing but a manifestation of this simple equation.

Where,
 y is the dependent variable i.e. the variable that needs to be estimated and
predicted.
 x is the independent variable i.e. the variable that is controllable. It is the
input.
 m is the slope. It determines what will be the angle of the line. It is the
parameter denoted as β.
 c is the intercept. A constant that determines the value of y when x is 0.
 We may recognize the equation for simple linear regression as the equation
for a sloped line on an x and y axis.
y = b0 + b1 * x1

Where ,
 b0 is constant.
 y is dependent variable
 B1 coefficient can be thought of as a multiplier that connects the independent
and dependent variables. It translates how much y will be affected by a unit
change in x. In other words, a change in x does not usually mean an equal
change in y.
 x1is an independent variable.

 Simple Linear Regression in Python :
#importing libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Importing the dataset
dataset = pd.read_csv('salary_data.csv')
x = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 1].values

# Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=1/3,
random_state=0)
# Fitting Simple Linear Regression to the Training set
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, y_train)

# Visualizing the Training set results
viz_train = plt
viz_train.scatter(X_train, y_train, color='red')
viz_train.plot(X_train, regressor.predict(X_train), color='blue')
viz_train.title('Salary VS Experience (Training set)')
viz_train.xlabel('Year of Experience')
viz_train.ylabel('Salary')
viz_train.show()
# Visualizing the Test set results
viz_test = plt
viz_test.scatter(X_test, y_test, color='red')
viz_test.plot(X_train, regressor.predict(X_train), color='blue')
viz_test.title('Salary VS Experience (Test set)')
viz_test.xlabel('Year of Experience')
viz_test.ylabel('Salary')
viz_test.show()

 After running above code excluding code explanations part, you can see 2
plots in the console window as shown below:

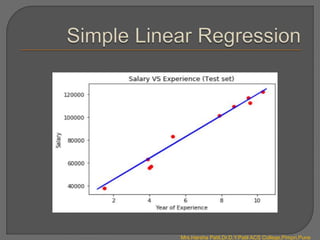
 One plot is from training set and another from test. Blue lines are in the
same direction. Our model is good to use now.
 Now we can use it to calculate (predict) any values of X depends on y or any
values of y depends on X. This can be done by using predict() function as
follows:
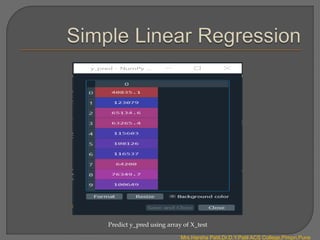
# Predicting the result of 5 Years Experience
y_pred =regressor.predict(np.array([5]).reshape(1, 1))
Output :
The value of y_pred with X = 5 (5 Years Experience) is 73545.90
You can offer to your candidate the salary of ₹ 73,545.90
and this is the best salary for him!

 In conclusion, with Simple Linear Regression, we have to do 5 steps as
per below:
 Importing the dataset.
 Splitting dataset into training set and testing set (2 dimensions of X and y
per each set). Normally, the testing set should be 5% to 30% of dataset.
 Visualize the training set and testing set to double check (you can bypass
this step if you want).
 Initializing the regression model and fitting it using training set (both X and
y).
 Let’s predict!!
We can also pass an array of X (of test set):
 # Predicting the Test set results
y_pred = regressor.predict(X_test)

Predict y_pred using array of X_test

2.Multiple Linear Regression :
 We have seen the concept of simple linear regression where a single
predictor variable x(years of experience) was used to model the response
variable y (Salary). In many applications, there is more than one factor that
effects the response. Multiple regression models describe how a single
response variable y depends linearly on a number of predictor variables.
 For Examples:
 The selling price of a house can depend on the desirability of the location,
the number of bedrooms, the number of bathrooms, the year the house was
built, the square footage of the plot and a number of other factors.
 The height of a child can rest on the height of the mother, the height of the
father, nutrition, and environmental factors.

 Multiple linear regression works the same way as that of simple linear
regression, except for the introduction of more independent variables and
their corresponding coefficients.
 In Simple Linear Regression we dealt with equation:
y = b0 + b1 * x1
With concerned to it, Multiple Linear Regression equation will become:
y = b0 + b1 * x1+ b2 * x2 + b3 * x3 + ………... +bn * xn
Or
i
Y= b0 + ∑ bn
1

 In translation, predicted value y is sum of all features multiplied with their
coefficients, summed with base coefficient b0.
Where,
 y is dependent variable/ predicted value.
 xi – features / independent variable / explanatory variable / observed
variable
 b0 is constant
 bn are coefficients that can be thought of as a multiplier that connects the
independent and dependent variables. It translates how much y will be
affected by a unit change in x. In other words, a change in x does not usually
mean an equal change in y.
Alternatively,
 So simplified, we are predicting what value of y will be depending on
features xi and with coefficients bi, we are deciding how much each feature
is affecting predicted value.

Multiple Linear Regression in Python :
#Importing libraries
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
dataset = pd.read_csv('salary_data.csv')
x = dataset.iloc[:, :-1].values
#Splitting the dataset into the Training set and Test set
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.2,
random_state = 0)

# Fitting Multiple Linear Regression to the Training set.
regressor = LinearRegression()
regressor.fit(X_train, y_train)
 Now! We have the Multiple Linear Regression model, we can use it to
calculate (predict) any values of x depends on y or any values of y depends
on x. This is how we do it as follows:
 ‘’’Predicting the result of salary of new employee with 5 Years of total
Experience, 2 years as team lead Experience, one year as project manager
and has 2 certifications’’’
x_new = [[5],[2],[1],[2]]
y_pred = regressor.predict(np.array(x_new).reshape(1, 4))
print(y_pred)
accuracy = (regressor.score(X_test,y_test))
print(accuracy)

Output :
The value of y_pred with x_new = [[5],[2],[1],[2]](5 Years of total Experience,
2 years as team lead, one year as project manager and 2 Certifications) is ₹
48017.20
You can offer to your candidate the salary of ₹48017.20 and this is the
best salary for him!

3.Polynomial Linear Regression :
 Polynomial regression is a form of regression analysis in which the
relationship between the independent variable x and the dependent
variable y is modelled as nth degree polynomial in x.
 Polynomial regression fits a nonlinear relationship between the value of x and
the corresponding conditional mean of y, denoted E(y |x).
 Although polynomial regression fits a nonlinear model to the data, as
a statistical estimation problem it is linear, in the sense that the regression
function E(y | x) is linear in the unknown parameters that are estimated from
the data.
 For this reason, polynomial regression is considered to be a special case
of multiple linear regression.

 For Example: Increment of salaryof employees per year is often non-linear.
We may express it in terms of polynomial Equation as
y = b0 + b1x+ b2x
2 + b3x
3 + ......+ bn x
n
where,
 b0 is constant .
 y is dependent variable
 bicoefficient can be thought of as a multiplier that connects the independent
and dependent variables. It translates how much y will be affected by a
degree or powerof change in x. In other words, a change in xi does not
usually mean an equal change in y.
 x is an independent variable.

 Let us consider dataset of this kind of example that represent the Polynomial
shape.

 To get an overview of the increment of salary, let’s visualize the data set into
a chart:

 Let’s think about our candidate. He has 5.5 Year of experience. What if we
use the Linear Regression in this example?

Polynomial Linear Regression in Python :
#Importing libraries
import numpy as np
import pandas as pd
dataset = pd.read_csv(‘position_salaries’)
X = dataset.iloc[:, 1:2].values

# Splitting the dataset into the Training set and Test set
from sklearn.model_selection importtrain_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,
random_state=0)
# Fitting Polynomial Regression to the dataset
from sklearn.preprocessing import PolynomialFeatures
poly_reg = PolynomialFeatures(degree=4)
X_poly = poly_reg.fit_transform(X)
pol_reg = LinearRegression()
pol_reg.fit(X_poly, y)

# Visualizing the Polynomial Regression results
def viz_polymonial():
plt.scatter(X, y, color='red')
plt.plot(X, pol_reg.predict(poly_reg.fit_transform(X)), color='blue')
plt.title('Truth or Bluff (Linear Regression)')
plt.xlabel('Position level')
plt.ylabel('Salary')
plt.show()
return
viz_polymonial()

# Additional feature
# Making the plot line (Blue one) more smooth
def viz_polymonial_smooth():
X_grid = np.arange(min(X), max(X), 0.1)
X_grid = X_grid.reshape(len(X_grid), 1)
# Visualizing the Polymonial Regression results
plt.scatter(X, y, color='red')
plt.plot(X_grid, pol_reg.predict(poly_reg.fit_transform(X_grid)), color='blue')
plt.title('Truth or Bluff (Linear Regression)')
plt.xlabel('Position level')
plt.ylabel('Salary')
plt.show()
return
viz_polymonial_smooth()

 After calling the viz_polynomial() function, you can see a plotting as per
below:

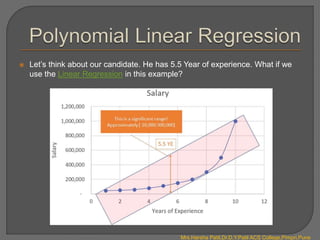
Last step, let’s predict the value of our candidate (with 5.5 YE) Polynomial
Regression model:
# Predicting a new result with Polymonial Regression
print(pol_reg.predict(poly_reg.fit_transform([[5.5]])))
Output:
It’s time to let our candidate know, we will offer him a best salary in class with₹
132,148!

 As we know linear regression, models a line to depicts the data points, while
a support vector regression (SVR), models a hyperplane to portrays or cover
the data points.
 Hyperplane is an area for margin of tolerance, set for approximation of
datapoints. The training instances inside to the hyperplane that helps to
define the margin are called Support Vectors.
 SVR tries to have as many support vectors as possible within the boundary
lines without much margin violation, thus keeping the error within the
threshold decided by the boundary lines of hyperplane.

 For Example: Stock price prediction as shown below

 Intuitively, support vectors contribute to the error ε made by the SVR called
threshold and thus, we want most of the support vectors to be in that
threshold. We can model SVR through kernels that indicate the similarity
measure between the test data point and the support vectors.
 A kernel is a set of mathematical functions which takes data as input and
transforms it into the form required by the output.
 Support Vector regression supports linear and non-linear regression. As it
seems in the above graph, the mission is to fit as many instances as
possible between the lines while limiting the margin violations. The violation
concept in this example represents as ε (epsilon).
 In regression problems, we generally try to find a line that best fits the data
provided. The equation of the line in its simplest form is described as y=mx
+c
 In the case of support vector regression, we do something similar but with a
slight change. Here we define a small error value e (error = prediction -
actual).

 The value of e determines the width of the error tube (also called insensitive
tube or hyper plane). The value of e determines the number of support
vectors, and a smaller e value indicates a lower tolerance for error.
 Thus, we try to find the line’s best fit in such a way that:
(mx+c)-y ≤ e and y-(mx+c) ≤ e
 Also, we do not care about errors as long, as they are less than e.
 For example, if we’re dealing with stock trading, and we want to minimize
the trading loss, but we do not care about loss as long as they are less than
a certain value (e).
 Hence, the support vector regression model depends only on a subset of the
training data points, as the cost function of the model ignores any training
data close to the model prediction when the error is less than e.
 In the field of machine learning, a support vector regression algorithm can, in
some cases, be more suitable for regression problems than other common
and popular algorithms. Below are the cases where a support vector
regression is advantageous over other regression algorithms:

 SVR is memory efficient, which means it takes a relatively lower amount of
calculation resources to train the model. This is because presenting the
solution by means of a small subset of training points gives enormous
computational advantages.
 There are non-linear or complex relationships between features and labels.
This is because we have the option to convert non-linear relationships to
higher-dimensional problems in the case of support vector regression.

 Decision trees are supervised learning algorithms used for both,
classification and regression.
 Decision trees are assigned to the information-based learning algorithms
which use different measures of information gain for learning. We can use
decision trees for issues where we have continuous but also categorical
input and target features.
 The main idea of decision trees is to find those descriptive features which
contain the most "information" regarding the target feature and then split the
dataset along the values of these features such that the target feature
values for the resulting sub datasets are as pure as possible.
 The descriptive feature which leaves the target feature most purely is said to
be the most informative one.
 This process of finding the "most informative" feature is done until we
accomplish a stopping criterion, where we then finally end up in so
called leaf nodes.

 The leaf nodes contain the predictions we will make for new query instances
presented to our trained model.
 This is possible since the model has kind of learned the underlying structure
of the training data and hence can, given some assumptions, make
predictions about the target feature value (class) of unseen query instances.
 A decision tree mainly contains of a root node, interior nodes, and leaf
nodes which are then connected by branches.

 Decision trees are sensitive to the specific data on which they are trained. If
the training data is changed the resulting decision tree can be quite different
and in turn the predictions can be quite different.
 Also, Decision trees are computationally expensive to train, carry a big risk
of overfitting (learning system tightly fits the given training data so much that
it would be inaccurate in predicting the outcomes of the untrained data.
In decision trees, over-fitting occurs when the tree is designed so as to
perfectly fit all samples in the training data set.), and tend to find local optima
because they can’t go back after they have made a split.
 To solve these weaknesses, we use Random Forest which illustrates the
power of combining many decision trees into one model.

 Random forest is a Supervised Learning algorithm which uses ensemble
learning method for classification and regression.
 An Ensemble method is a technique that combines the predictions from
multiple machine learning algorithms together to make more accurate
predictions than any individual model. A model comprised of many models is
called an Ensemble model.

Types of Ensemble Learning:
 Boosting.
 Bootstrap Aggregation (Bagging).
1. Boosting
Boosting refers to a group of algorithms that utilize weighted averages to
make weak learners into stronger learners. Boosting is all about “teamwork”.
Each model that runs, dictates what features the next model will focus
on.In boosting as the name suggests, one is learning from other which in
turn boosts the learning.
2. Bootstrap Aggregation (Bagging)
Bootstrap allows us to better understand the bias and the variance with the
dataset. Bootstrap involves random sampling of small subset of data from
the dataset.Bagging makes each model run independently and
then aggregates the outputs at the end without preference to any model.

Thanks !!!

Introduction to Regression . pptx

More Related Content

Similar to Introduction to Regression . pptx

More from Harsha Patil

Recently uploaded

Introduction to Regression . pptx