Downloaded 13 times
Uploaded byDavide Eynard
Laplacian Colormaps: a framework for structure-preserving color transformations
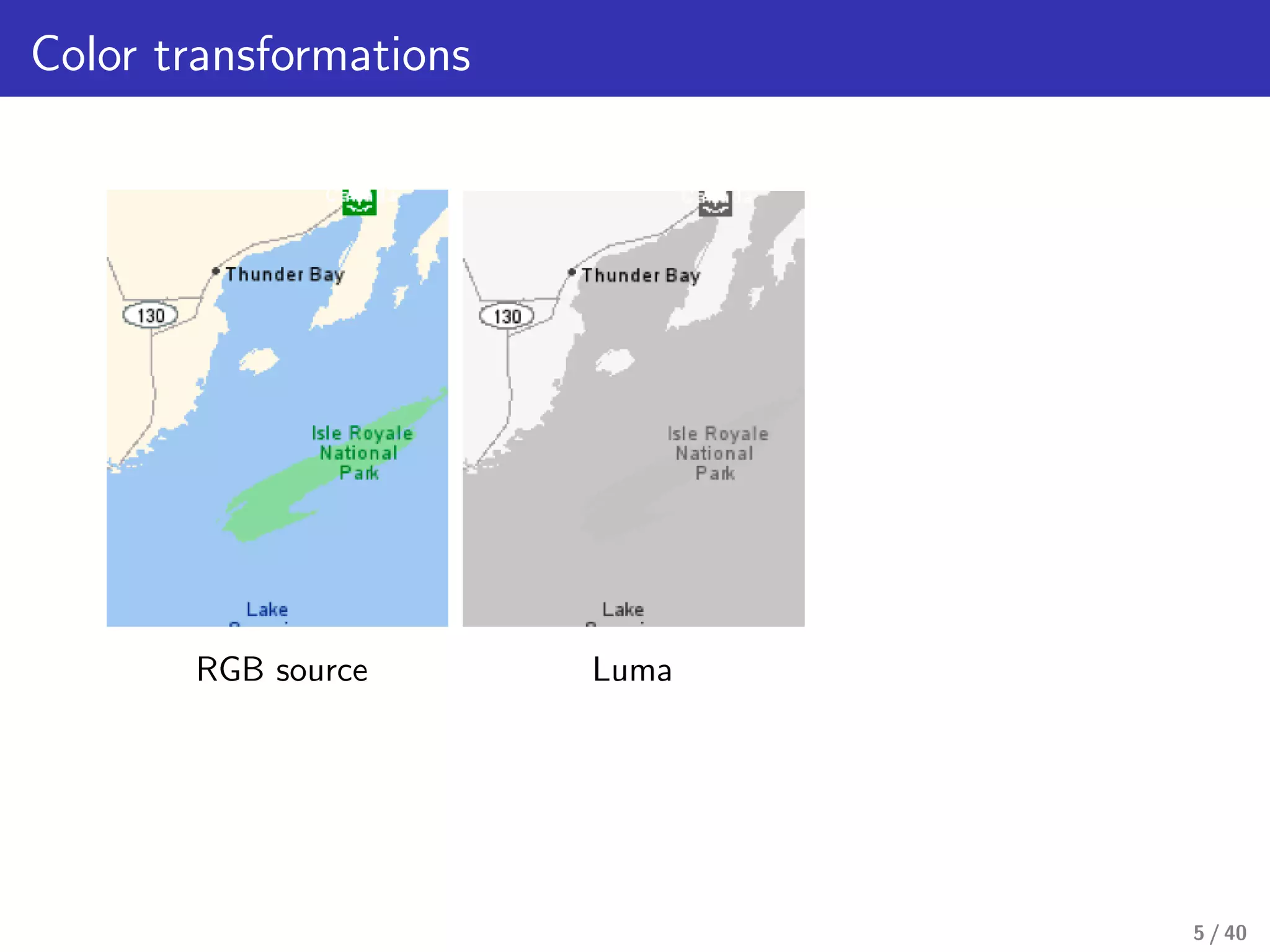
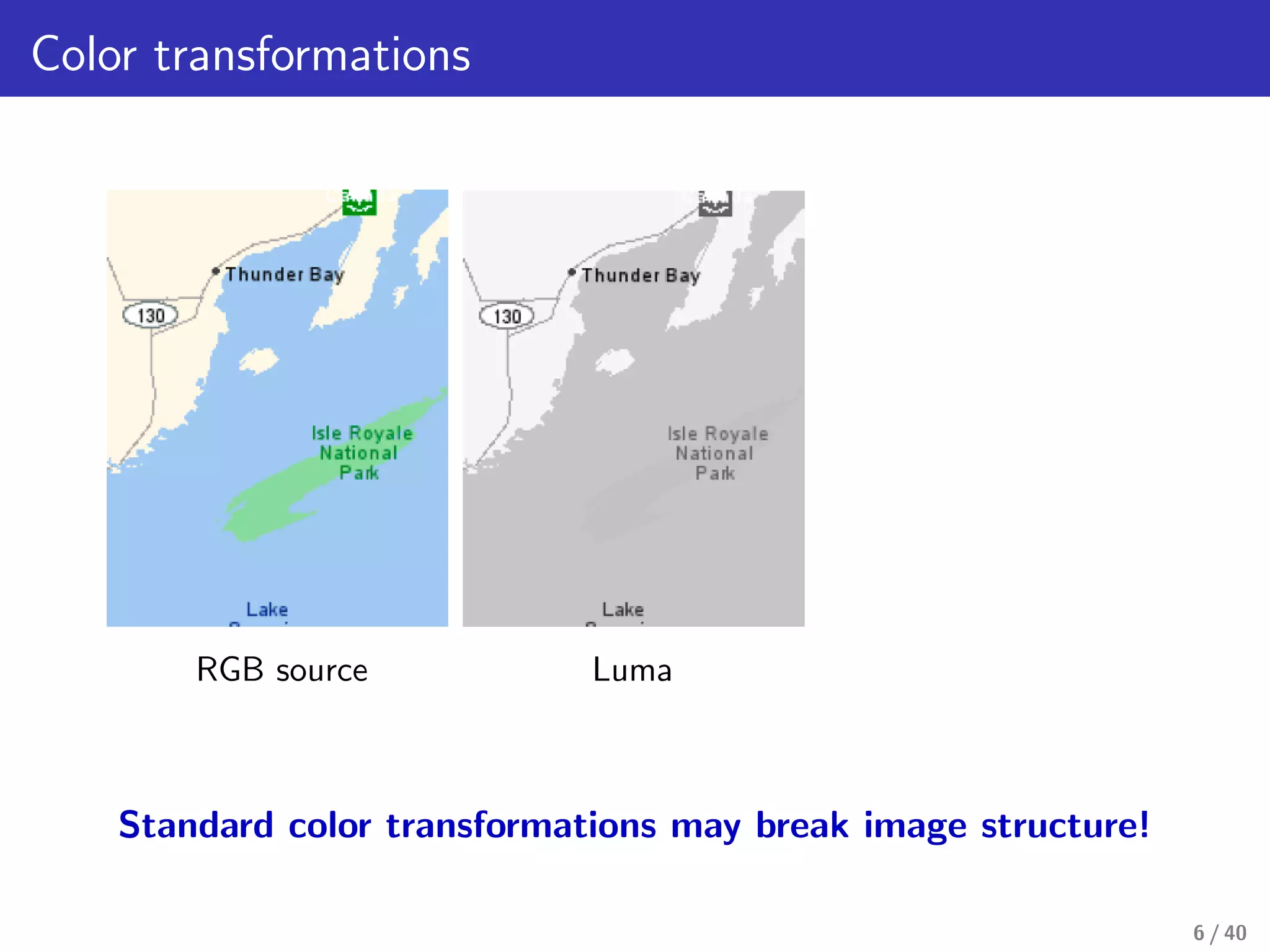
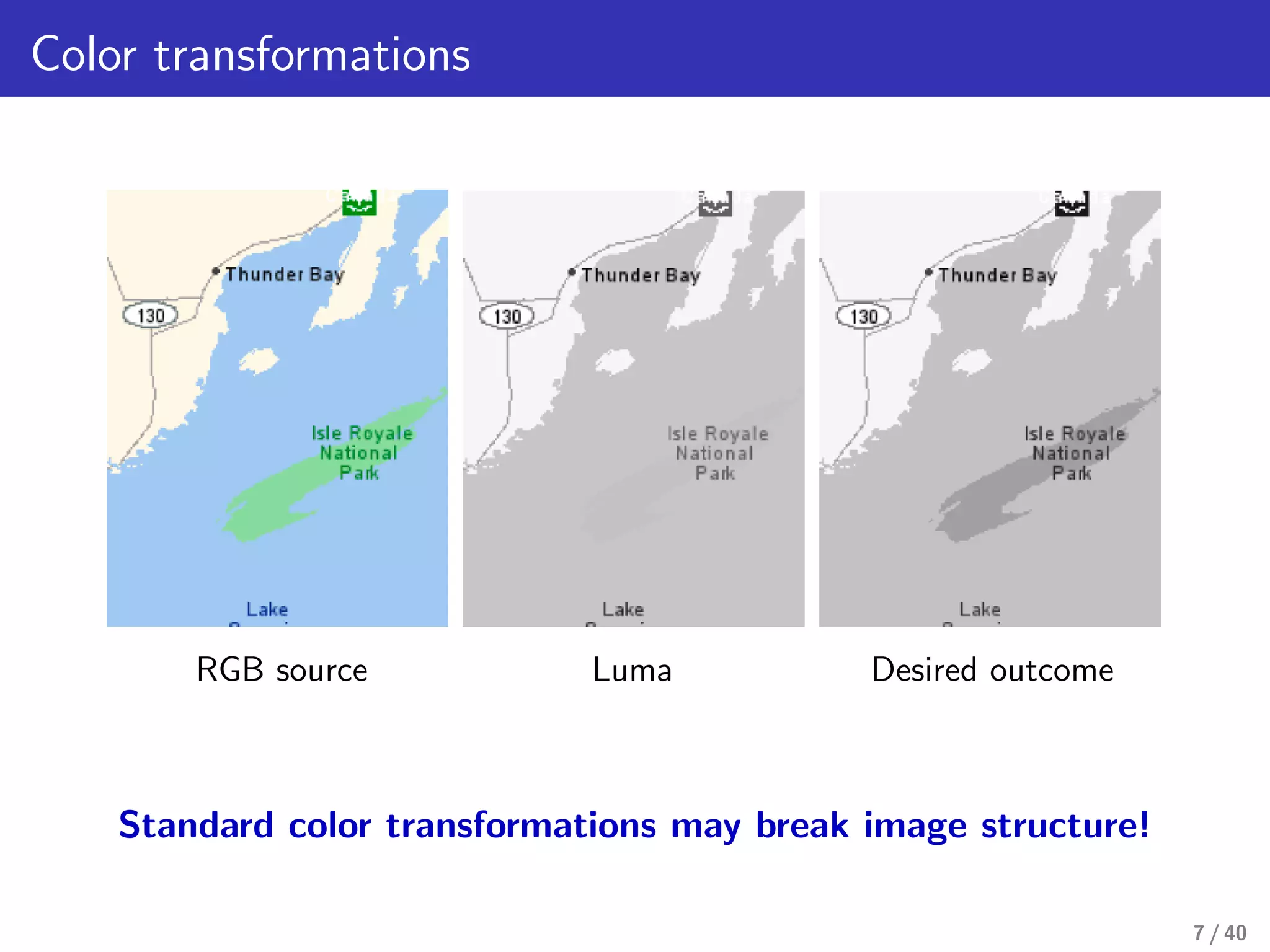
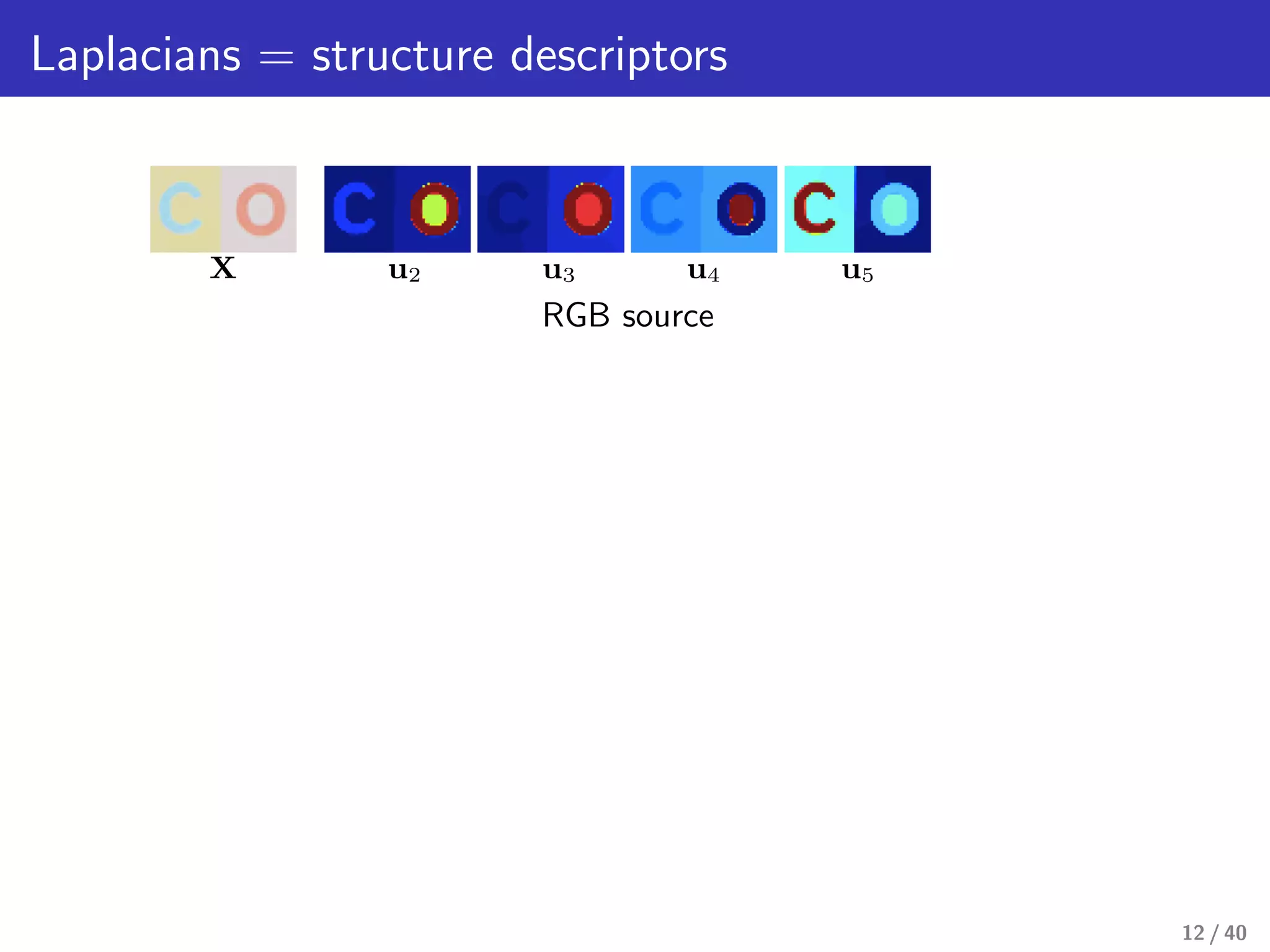
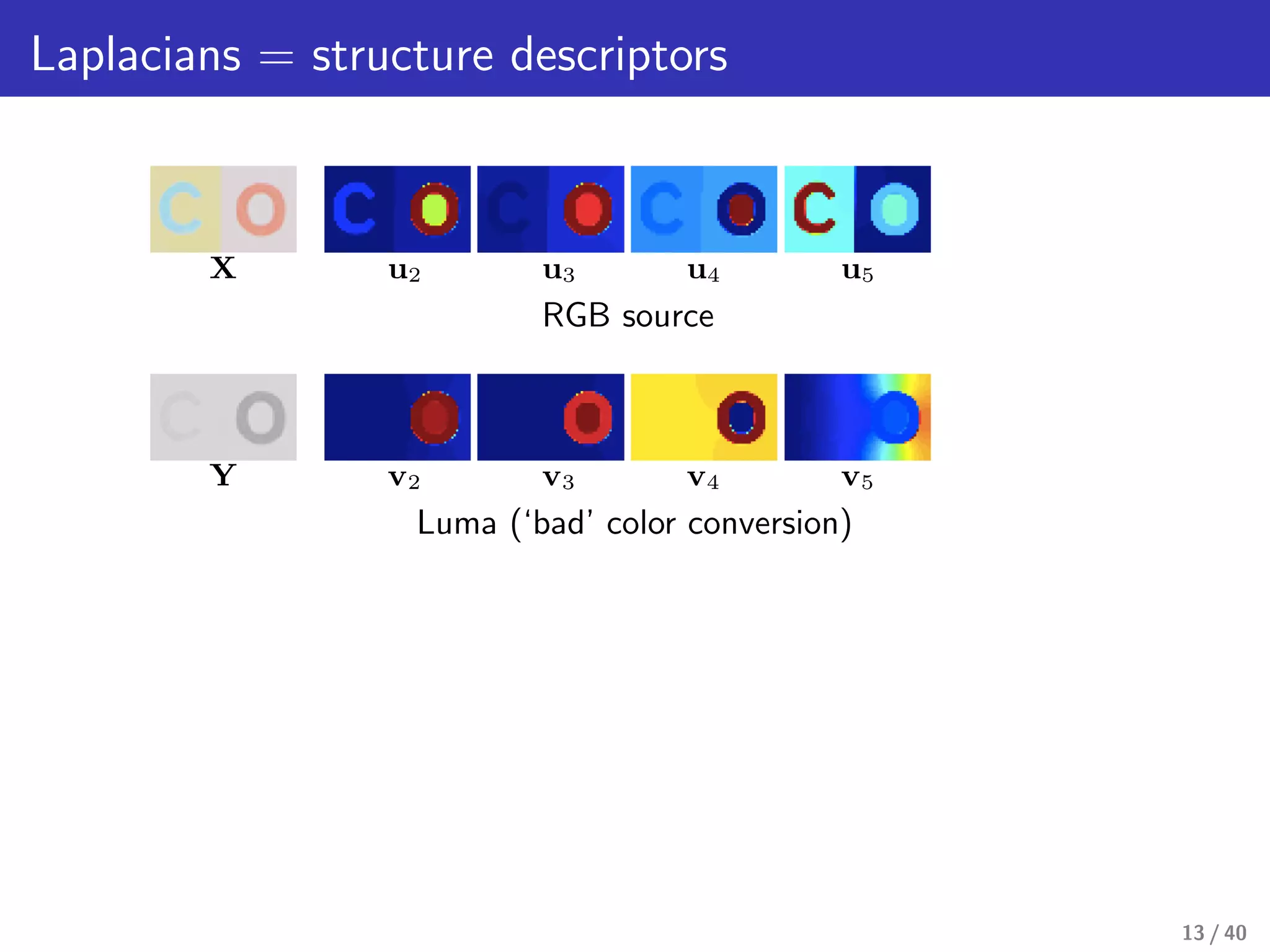
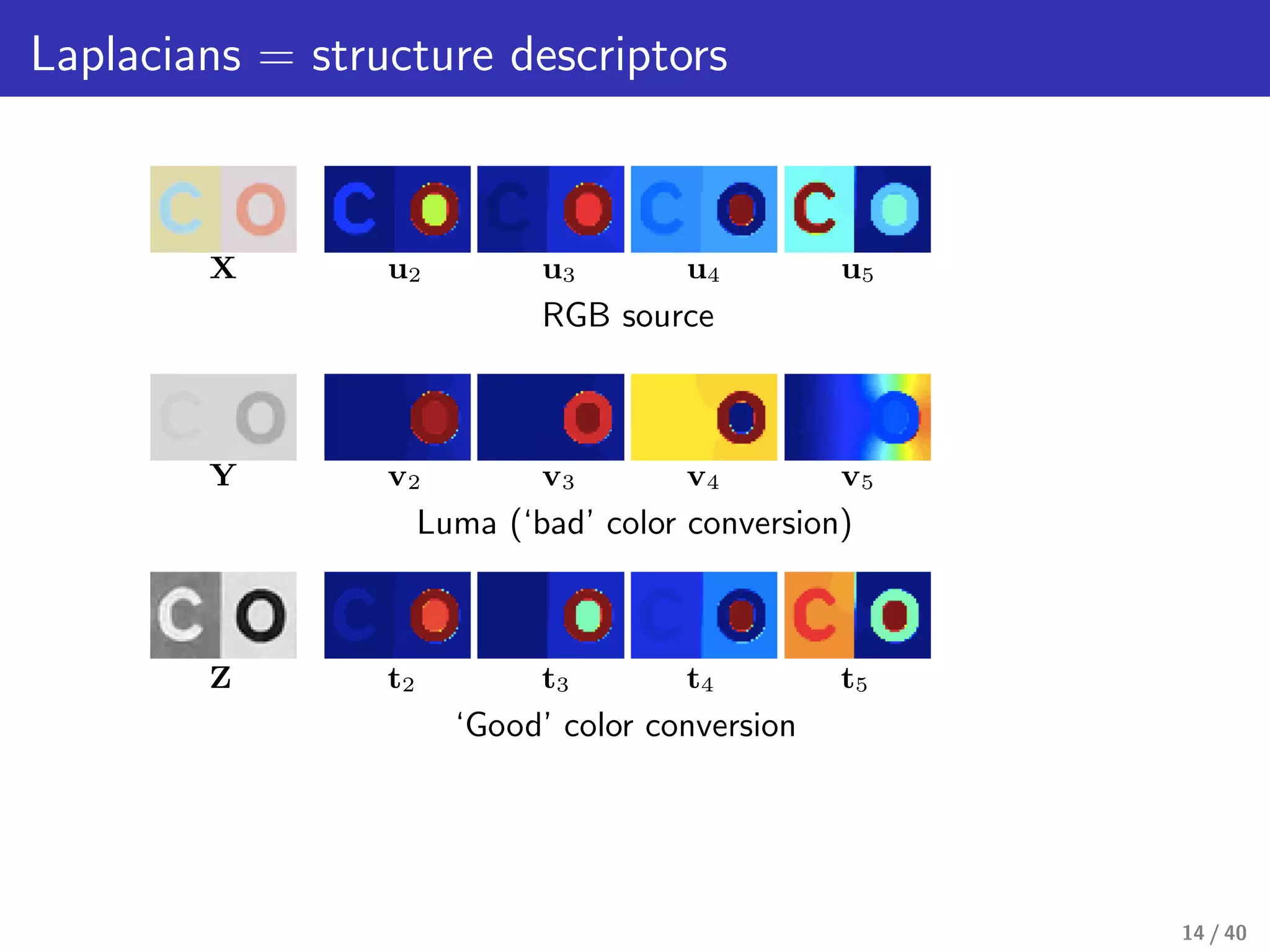
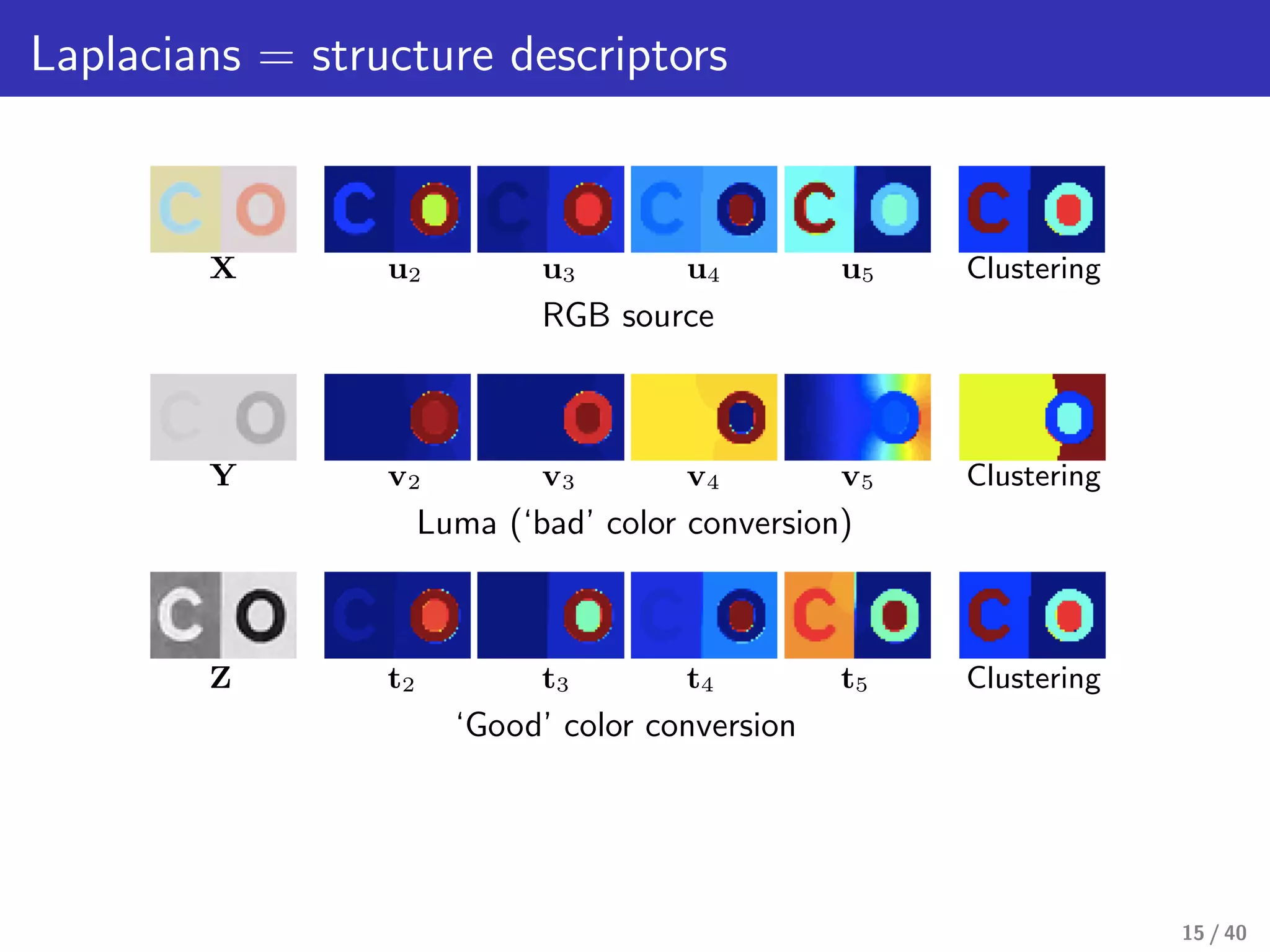
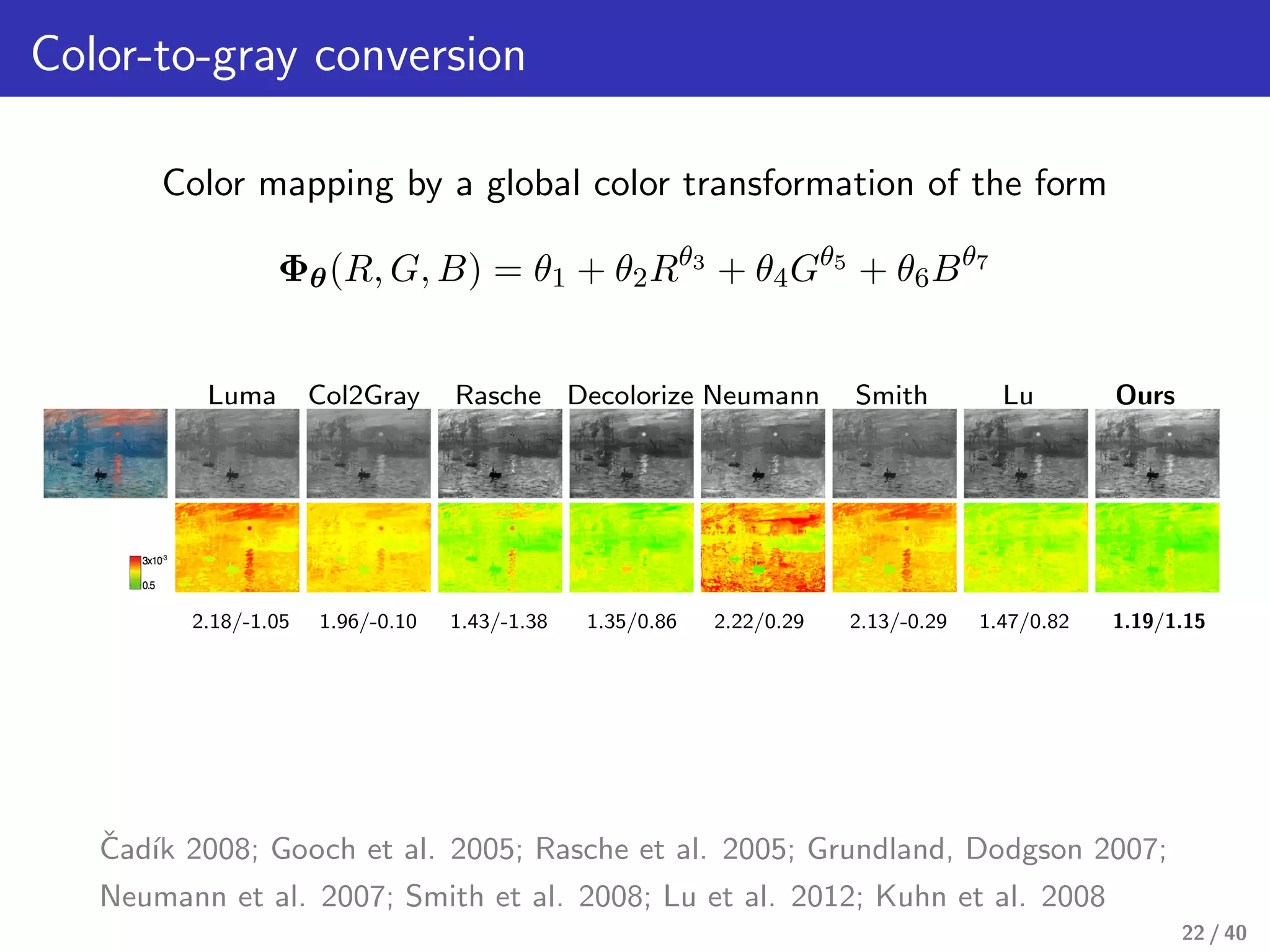
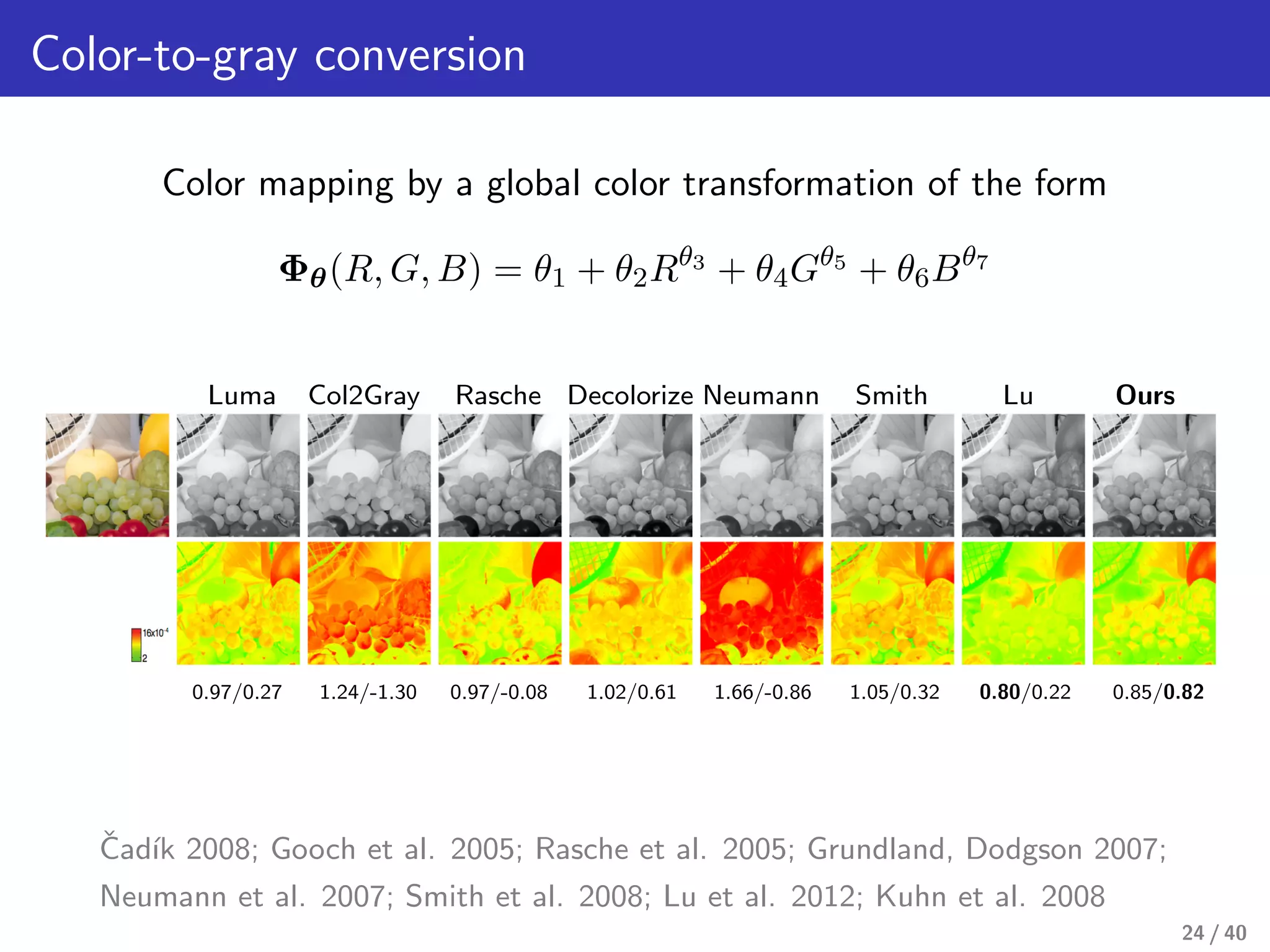
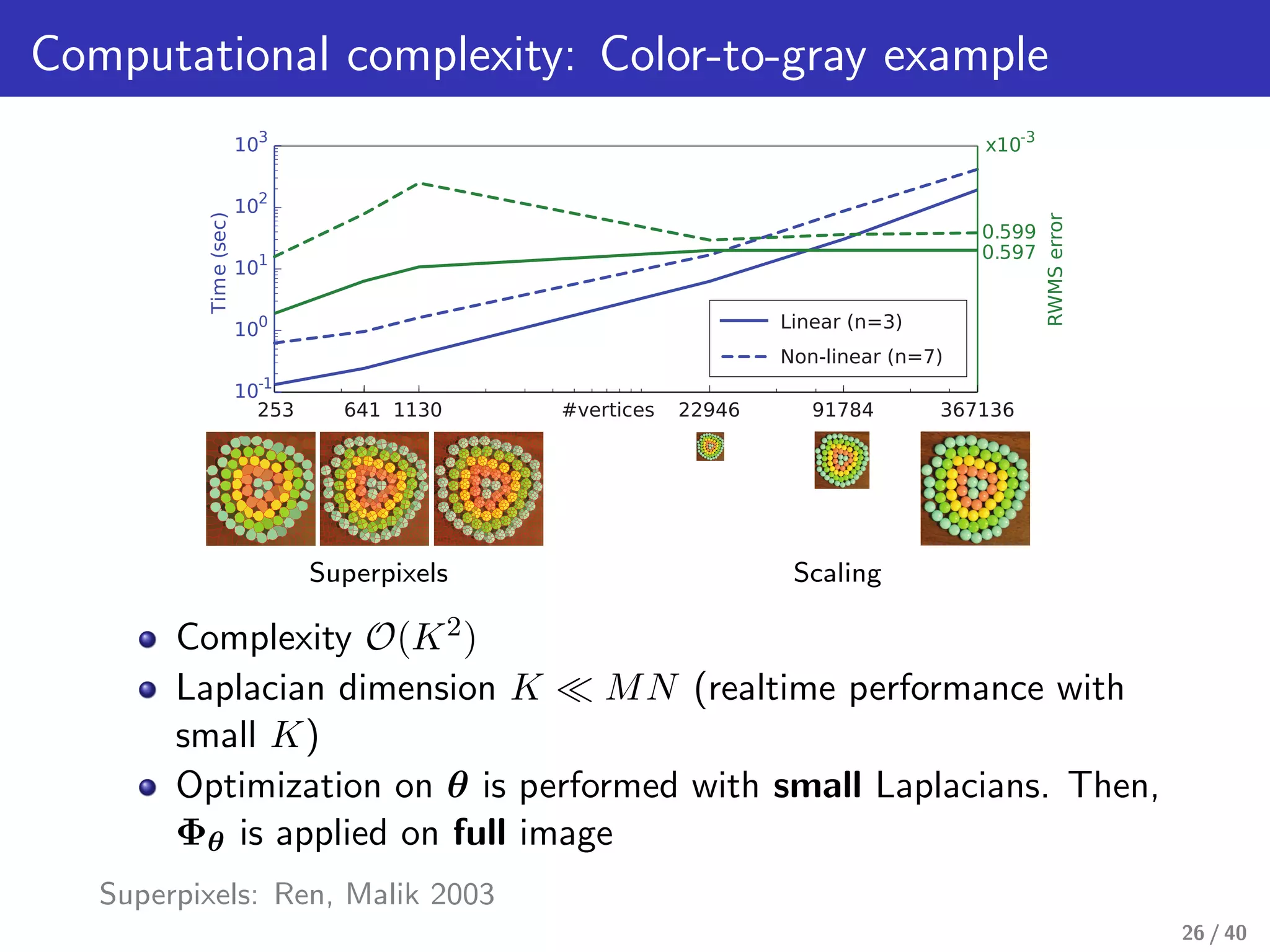
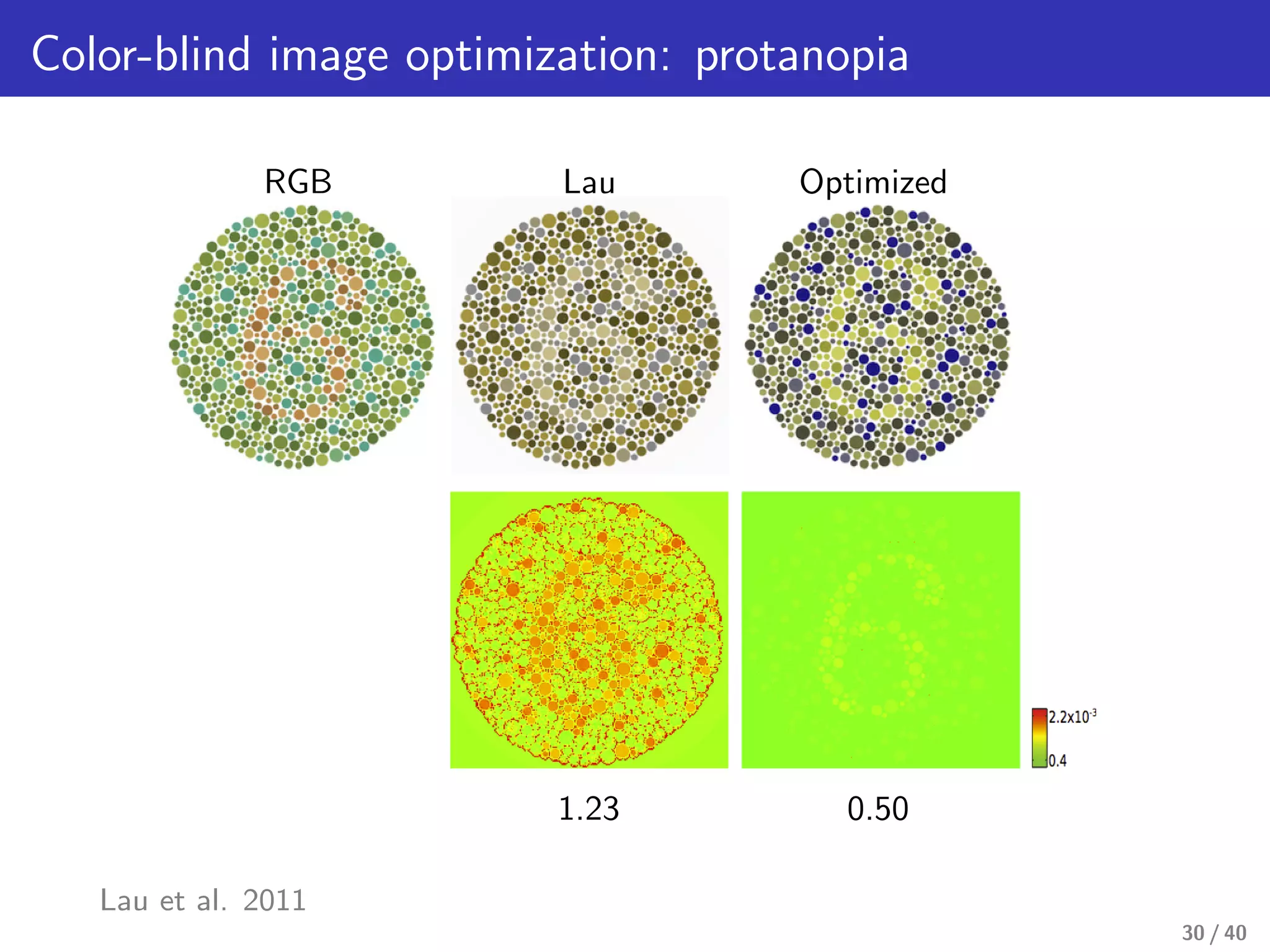
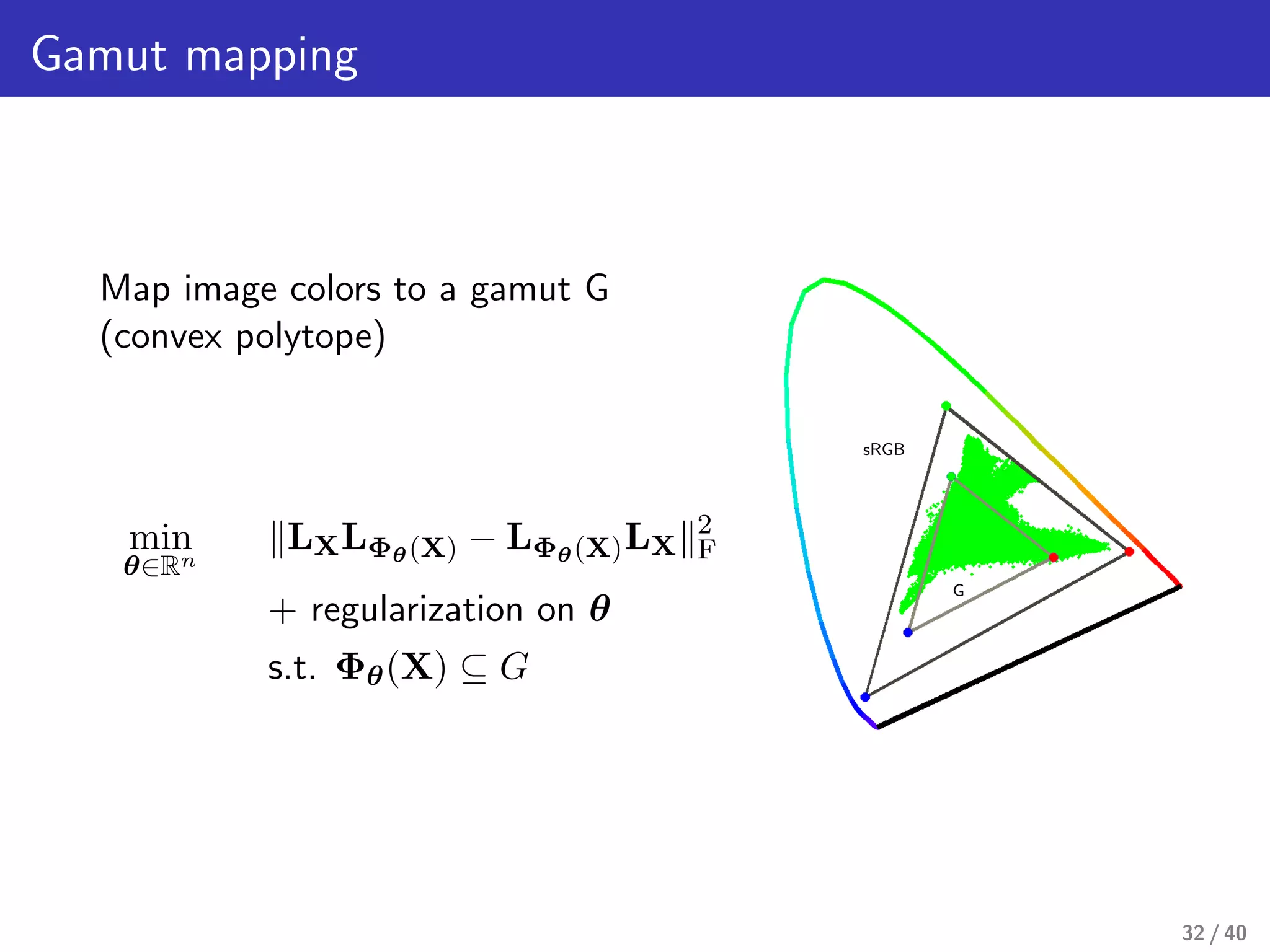
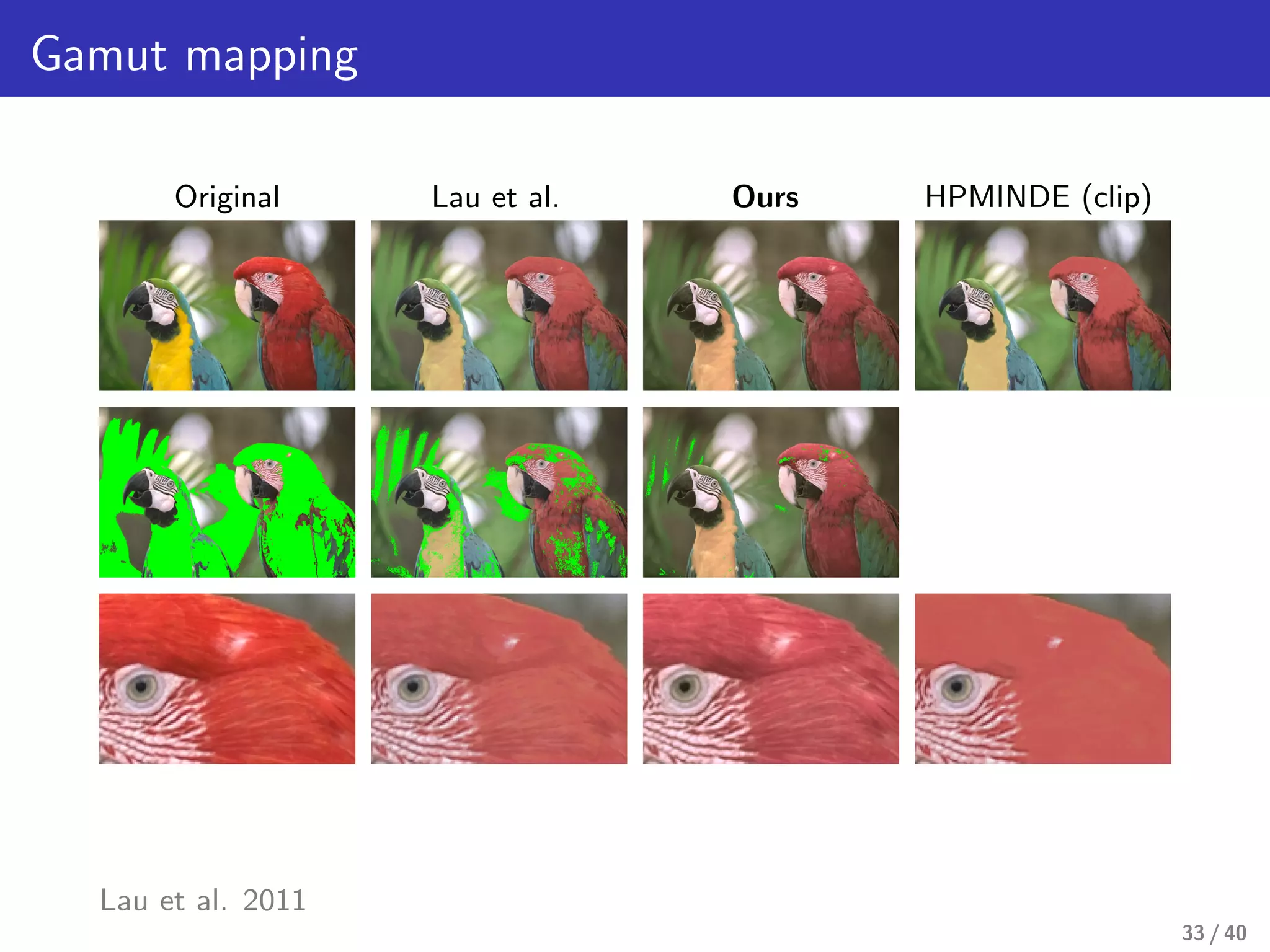
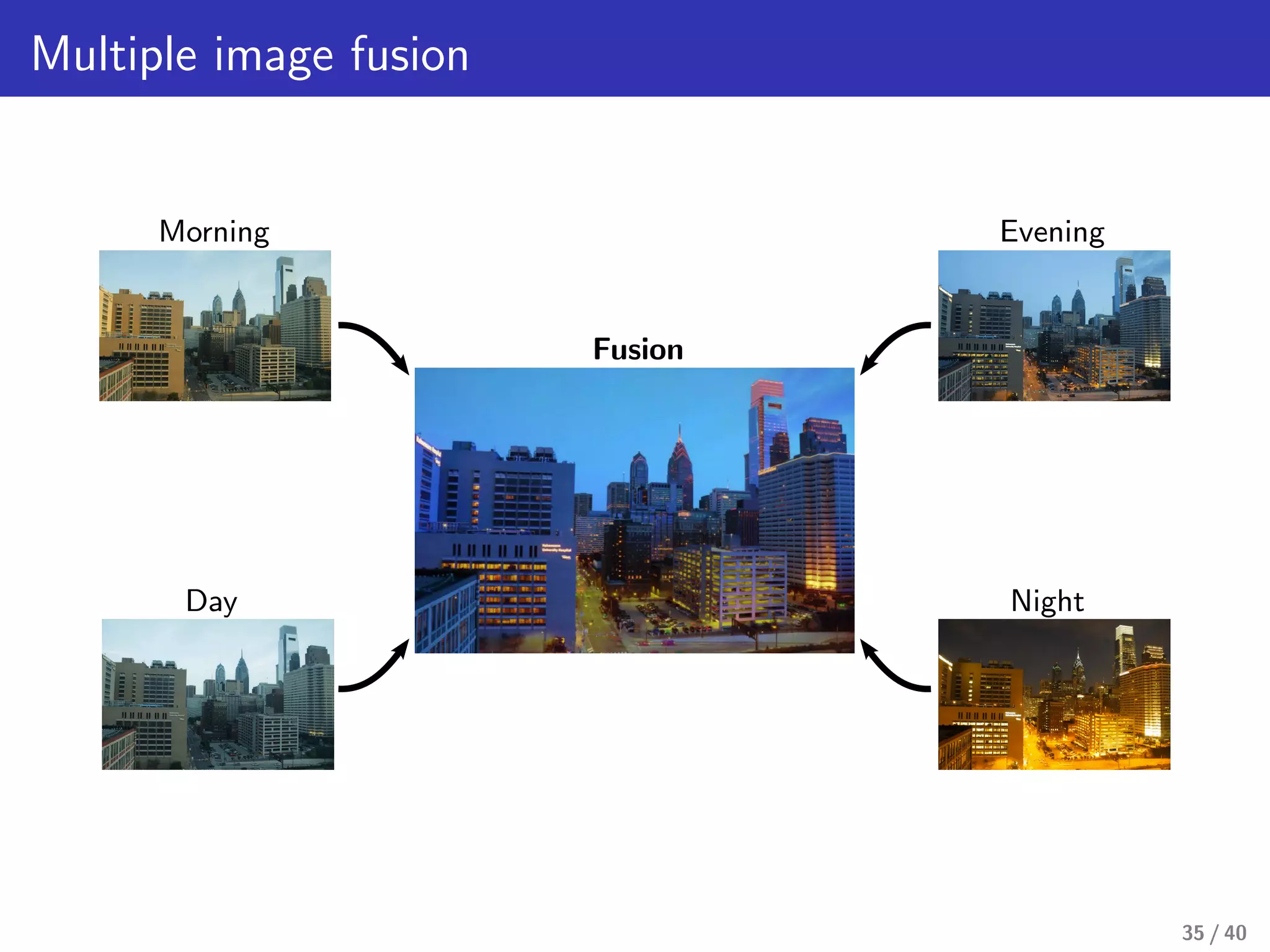
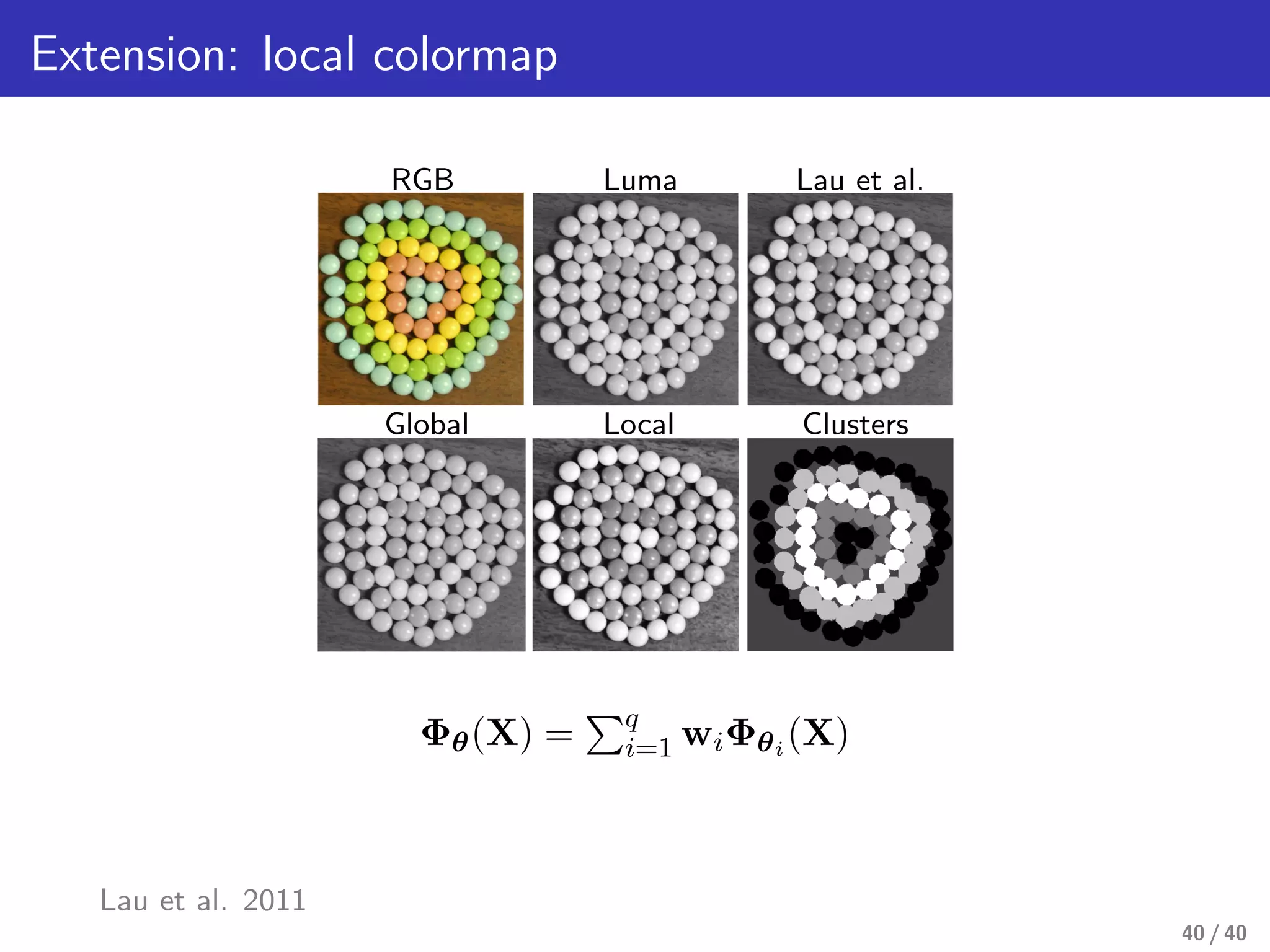
This document presents a framework for structure-preserving color transformations using Laplacian colormaps. (1) It represents images as graphs with Laplacian matrices that encode image structure. (2) It finds joint eigenbases of Laplacians to perform color transformations that minimally distort structure. (3) It applies this approach to applications like color-to-gray conversion, colorblind optimization, gamut mapping, and multispectral image fusion. The results demonstrate high-quality color transformations while preserving image structure.
More Related Content
![[Question Paper] Advanced SQL (Old Course) [April / 2015]](https://cdn.slidesharecdn.com/ss_thumbnails/sql-qpoldcourseapr-2015-170717052004-thumbnail.jpg?width=640&height=640&fit=bounds)
Similar to Laplacian Colormaps: a framework for structure-preserving color transformations
![[SIGGRAPH 2016] Automatic Image Colorization](https://cdn.slidesharecdn.com/ss_thumbnails/iizukasiggraph2016slide-170809084052-thumbnail.jpg?width=640&height=640&fit=bounds)
Laplacian Colormaps: a framework for structure-preserving color transformations
- 1. Laplacian colormaps: aframework for structure-preserving color transformations Davide Eynard, Artiom Kovnatsky, Michael Bronstein Institute of Computational Science, Faculty of Informatics University of Lugano, Switzerland Eurographics, 8 April 2014 This research was supported by the ERC Starting Grant No. 307047 (COMET). 1 / 40
- 2.
- 3.
- 4.
- 5. Color transformations RGB sourceLuma 5 / 40
- 6. Color transformations RGB sourceLuma Standard color transformations may break image structure! 6 / 40
- 7. Color transformations RGB sourceLuma Desired outcome Standard color transformations may break image structure! 7 / 40
- 8. Image Laplacian Input N× M image with d color channels, column-stacked into an NM × d matrix X Represented as graph with K vertices (e.g. superpixels) and weighted edges 8 / 40
- 9. Image Laplacian Input N× M image with d color channels, column-stacked into an NM × d matrix X Represented as graph with K vertices (e.g. superpixels) and weighted edges K × K adjacency matrix WX wij = exp − δ2 ij 2σ2 s + xki − xkj 2 2 2σ2 r K × K Laplacian LX = DX−WX, DX = diag( j=i wij) xki xkj wij 9 / 40
- 10. Laplacians = structuredescriptors UT LXU = ΛX, VT LYV = ΛY X u4 u5 u6 u7 Y v4 v5 v6 v7 Similar structure ⇐⇒ similar Laplacian eigenvectors 10 / 40
- 11. Laplacians = structuredescriptors UT LXU = ΛX, VT LYV = ΛY X u4 u5 u6 u7 Y v4 v5 v6 v7 Similar structure ⇐⇒ similar Laplacian eigenvectors Ideally, two Laplacians are jointly diagonalizable (iff they commute): there exists a joint eigenbasis ˆU = U = V 11 / 40
- 12. Laplacians = structuredescriptors X u2 u3 u4 u5 RGB source 12 / 40
- 13. Laplacians = structuredescriptors X u2 u3 u4 u5 RGB source Y v2 v3 v4 v5 Luma (‘bad’ color conversion) 13 / 40
- 14. Laplacians = structuredescriptors X u2 u3 u4 u5 RGB source Y v2 v3 v4 v5 Luma (‘bad’ color conversion) Z t2 t3 t4 t5 ‘Good’ color conversion 14 / 40
- 15. Laplacians = structuredescriptors X u2 u3 u4 u5 Clustering RGB source Y v2 v3 v4 v5 Clustering Luma (‘bad’ color conversion) Z t2 t3 t4 t5 Clustering ‘Good’ color conversion 15 / 40
- 16. Finding joint eigenbases Jointapproximate diagonalization Find joint approximate eigenbasis ˆU min ˆU off( ˆU T LX ˆU) + off( ˆU T LY ˆU) s.t. ˆU T ˆU = I where off(A) = i=j a2 ij. Cardoso 1995, Eynard et al. 2012, Kovnatsky et al. 2013 16 / 40
- 17. Finding joint eigenbases Jointapproximate diagonalization Find joint approximate eigenbasis ˆU min ˆU off( ˆU T LX ˆU) + off( ˆU T LY ˆU) s.t. ˆU T ˆU = I where off(A) = i=j a2 ij. Closest commuting Laplacians Find closest commuting pair ˜LX, ˜LY min ˜LX,˜LY ˜LX − LX 2 F + ˜LY − LY 2 F s.t. ˜LX ˜LY = ˜LY ˜LX Since ˜LX and ˜LY commute, they have a joint eigenbasis ˆU Cardoso 1995, Eynard et al. 2012, Kovnatsky et al. 2013, Bronstein et al. 2013 17 / 40
- 18. Finding joint eigenbases Jointapproximate diagonalization Find joint approximate eigenbasis ˆU min ˆU off( ˆU T LX ˆU) + off( ˆU T LY ˆU) s.t. ˆU T ˆU = I where off(A) = i=j a2 ij. Closest commuting Laplacians Find closest commuting pair ˜LX, ˜LY min ˜LX,˜LY ˜LX − LX 2 F + ˜LY − LY 2 F s.t. ˜LX ˜LY = ˜LY ˜LX Since ˜LX and ˜LY commute, they have a joint eigenbasis ˆU These two problems are equivalent! (approx. joint diagonalizability ⇐⇒ approx. commutativity) Cardoso 1995, Eynard et al. 2012, Kovnatsky et al. 2013, Bronstein et al. 2013 18 / 40
- 19.
- 20. Laplacian colormaps X −→ Φθ Y =Φθ(X) Parametric colormap Φθ : RNM×d → RNM×d parametrized by θ = (θ1, . . . , θn) Global: each pixel x is transformed same way, y = Φθ(x) Local: different transformations in q regions, Φθ(X) = q i=1 wiΦθi (X) 20 / 40
- 21. Laplacian colormaps X −→ Φθ Y =Φθ(X) LX LY LX = DX − WX LΦθ(X) = DΦθ(X) − WΦθ(X) Find an optimal parametric color transformation min θ∈Rn LXLΦθ(X) − LΦθ(X)LX 2 F + regularization on θ 21 / 40
- 22. Color-to-gray conversion Color mappingby a global color transformation of the form Φθ(R, G, B) = θ1 + θ2Rθ3 + θ4Gθ5 + θ6Bθ7 Luma Col2Gray Rasche Decolorize Neumann Smith Lu Ours 2.18/-1.05 1.96/-0.10 1.43/-1.38 1.35/0.86 2.22/0.29 2.13/-0.29 1.47/0.82 1.19/1.15 ˇCad´ık 2008; Gooch et al. 2005; Rasche et al. 2005; Grundland, Dodgson 2007; Neumann et al. 2007; Smith et al. 2008; Lu et al. 2012; Kuhn et al. 2008 22 / 40
- 23. Color-to-gray conversion Color mappingby a global color transformation of the form Φθ(R, G, B) = θ1 + θ2Rθ3 + θ4Gθ5 + θ6Bθ7 Luma Col2Gray Rasche Decolorize Neumann Smith Lu Ours 5.01/-0.55 3.42/-0.89 3.59/-0.48 3.44/1.41 5.44/-0.66 5.04/-0.19 2.90/0.50 1.28/0.86 9.27/-0.57 7.05/-0.53 7.20/-0.04 7.28/1.45 10.17/-1.05 9.13/-1.02 6.30/1.01 3.78/0.76 ˇCad´ık 2008; Gooch et al. 2005; Rasche et al. 2005; Grundland, Dodgson 2007; Neumann et al. 2007; Smith et al. 2008; Lu et al. 2012; Kuhn et al. 2008 23 / 40
- 24. Color-to-gray conversion Color mappingby a global color transformation of the form Φθ(R, G, B) = θ1 + θ2Rθ3 + θ4Gθ5 + θ6Bθ7 Luma Col2Gray Rasche Decolorize Neumann Smith Lu Ours 0.97/0.27 1.24/-1.30 0.97/-0.08 1.02/0.61 1.66/-0.86 1.05/0.32 0.80/0.22 0.85/0.82 ˇCad´ık 2008; Gooch et al. 2005; Rasche et al. 2005; Grundland, Dodgson 2007; Neumann et al. 2007; Smith et al. 2008; Lu et al. 2012; Kuhn et al. 2008 24 / 40
- 25. Color-to-gray conversion Color mappingby a global color transformation of the form Φθ(R, G, B) = θ1 + θ2Rθ3 + θ4Gθ5 + θ6Bθ7 Luma Col2Gray Rasche Decolorize Neumann Smith Lu Ours RWMS 2.84 2.31 2.46 2.20 4.85 2.94 1.90 1.33 z-score -0.17 -0.31 -0.63 0.55 -0.53 -0.09 0.34 0.84 ˇCad´ık 2008; Gooch et al. 2005; Rasche et al. 2005; Grundland, Dodgson 2007; Neumann et al. 2007; Smith et al. 2008; Lu et al. 2012; Kuhn et al. 2008 25 / 40
- 26. Computational complexity: Color-to-grayexample 10-1 100 101 102 103 Time(sec) #vertices253 641 1130 22946 91784 367136 0.597 RWMSerror 0.599 x10-3 Linear (n=3) Non-linear (n=7) Superpixels Scaling Complexity O(K2) Laplacian dimension K MN (realtime performance with small K) Optimization on θ is performed with small Laplacians. Then, Φθ is applied on full image Superpixels: Ren, Malik 2003 26 / 40
- 27. Color-blind image optimization RGBsource X Ψ Seen by color-blind Ψ(X) Vi´enot et al. 1999, Kim et al. 2012 27 / 40
- 28. Color-blind image optimization RGBsource X Φθ(X) Ψ Seen by color-blind Φθ (Φθ ◦ Ψ)(X) 28 / 40
- 29. Color-blind image optimization RGBsource X Φθ(X) Ψ Seen by color-blind Φθ (Φθ ◦ Ψ)(X) LXLΦθ(X)−LΦθ(X)LX LXL(Φθ◦Ψ)(X)−L(Φθ◦Ψ)(X)LX 29 / 40
- 30. Color-blind image optimization:protanopia RGB Lau 1.23 Optimized 0.50 Lau et al. 2011 30 / 40
- 31. Color-blind image optimization:tritanopia RGB Lau 1.69 Optimized 0.53 Lau et al. 2011 31 / 40
- 32. Gamut mapping Map imagecolors to a gamut G (convex polytope) min θ∈Rn LXLΦθ(X) − LΦθ(X)LX 2 F + regularization on θ s.t. Φθ(X) ⊆ G sRGB G 32 / 40
- 33. Gamut mapping Original Lauet al. Ours HPMINDE (clip) Lau et al. 2011 33 / 40
- 34. RGB+NIR fusion NIR RGBLau et al. Ours Lau et al. 2011 34 / 40
- 35.
- 36.
- 37. Summary Framework theoretically grounded versatile global/local realtime Applications color-to-grayscale color-blind optimization gamutmapping multispectral image fusion 37 / 40
- 38.
- 39. Qualitative evaluation Web survey 124volunteers, 2884 pairwise evaluations Thurstone’s law of comparative judgements → z-score Consistent with ˇCad´ık’s results 39 / 40
- 40. Extension: local colormap RGBLuma Lau et al. Global Local Clusters Φθ(X) = q i=1 wiΦθi (X) Lau et al. 2011 40 / 40