k-MLE: A fast algorithm for learning statistical mixture models

k-MLE:
A fast algorithm for learning statistical mixture models
(arXiv:1203.5181)
Frank NIELSEN
Sony Computer Science Laboratories, Inc.
28th March 2012
International Conference on Acoustics, Speech, and Signal Processing
ICASSP, Kyoto ICC

c 1997-2012 Frank Nielsen, Sony Computer Science Laboratories, Inc. 1/28

Outline
I Background
I Statistical mixtures of exponential families (EFMMs)
I Legendre transform and mixture dual parameterizations
I Contributions
I k-MLE and its variants
I k-MLE initialization (k-MLE++)
I Summary


Exponential Family Mixture Models (EFMMs)
Generalize Gaussian & Rayleigh MMs to many common
distributions.
m(x) =
Xk
i=1
wipF (x; i ) with 8i wi 0,
Pk
i=1 wi = 1
pF (x; ) = eht(x),i−F()+k(x)
F: log-Laplace transform (partition, cumulant function):
Z
x2X
pF (x; )dx = 1 ) F() = log
Z
x2X
eht(x),i+k(x)dx,
2 =

|
Z
x2X
eht(x),i+k(x)dx 1

the natural parameter space.
I d: Dimension of the support X.
I D: order of the family (= dim). Statistic: t(x) : Rd ! RD.


Statistical mixtures: Rayleigh MMs [7, 5]
IntraVascular UltraSound (IVUS) imaging:
Rayleigh distribution:
p(x; ) = x
2 e− x2
22
x 2 R+ = X
d = 1 (univariate)
D = 1 (order 1)
= − 1
22
= (−1, 0)
F() = −log(−2)
t(x) = x2
k(x) = log x
(Weibull k = 2)
Coronary plaques: fibrotic tissues, calcified tissues, lipidic tissues
Rayleigh Mixture Models (RMMs):
for segmentation and classification tasks


Statistical mixtures: Gaussian MMs [3, 5]
Gaussian mixture models (GMMs).
Color image interpreted as a 5D xyRGB point set.
Gaussian distribution p(x; μ,):
1
(2)
d
2p||
e−1
2D−1 (x−μ,x−μ)
Squared Mahalanobis distance:
DQ(x, y) = (x − y)TQ(x − y)
x 2 Rd = X
d (multivariate)
D = d(d+3)
2 (order)
= (−1μ, 1
2−1) = (v , M)
= R × Sd+
+
F() = 1
v −1
4 T
M v − 1
2 log |M| +
d
2 log
t(x) = (x,−xxT )
k(x) = 0


Sampling from a Gaussian Mixture Model (GMM)
To sample a variate x from a GMM:
I Choose a component l according to the weight distribution
w1, ...,wk ,
I Draw a variate x according to N(μl ,l ).
Doubly stochastic process:
1. throw a (biased) dice with k faces to choose the component:
l Multinomial(w1, ...,wk )
(Multinomial distribution belongs also to the exponential
families.)
2. then draw at random a variate x from the l -th component
x Normal(μl ,l )
x = μ + Cz with Cholesky: = CCT and z = [z1 ... zd ]T
standard normal random variate: zi = p−2 log U1 cos(2U2)


Statistical mixtures: Generative models of data sets
GMM = feature descriptor for information retrieval (IR)
! classification, matching, etc.
Increase dimension using color image patches.
Low-frequency information encoded into compact statistical model.
Generative model ! statistical image by GMM sampling.
Source GMM Sample


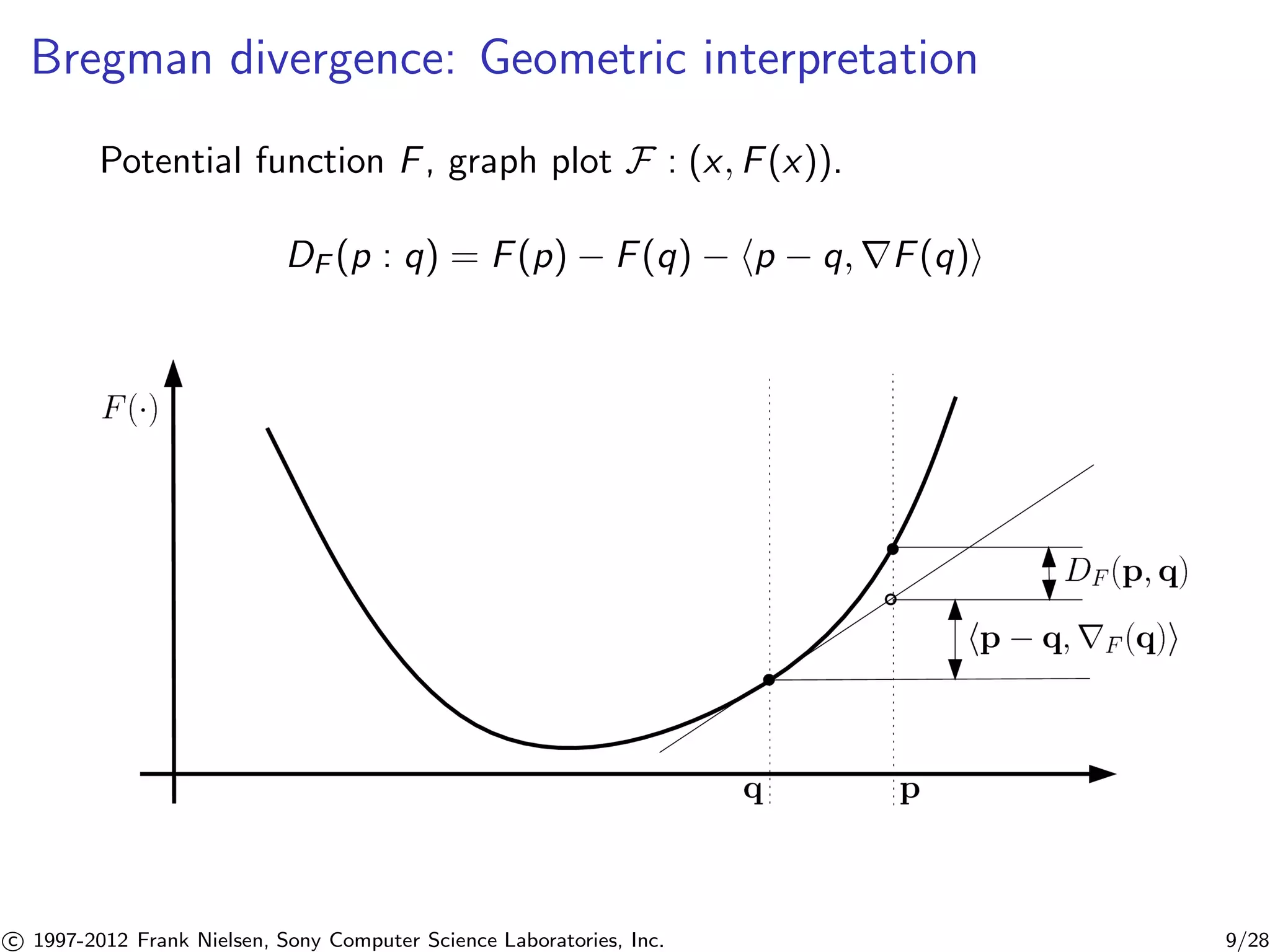
Distance between exponential families: Relative entropy
I Distance between features (e.g., GMMs)
I Kullback-Leibler divergence (cross-entropy minus entropy):
KL(P : Q) =
Z
p(x) log
p(x)
q(x)
dx 0
=
Z
p(x) log
1
q(x)
dx
| {z }
H×(P:Q)
−
Z
p(x) log
1
p(x)
dx
| {z }
H(p)=H×(P:P)
= F(Q) − F(P) − hQ − P,rF(P)i
= BF (Q : P)
Bregman divergence BF defined for a strictly convex and
differentiable function (up to some affine terms).
I Proof KL(P : Q) = BF (Q : P) follows from
X EF () =) E[t(X)] = rF()


Bregman divergence: Geometric interpretation
Potential function F, graph plot F : (x, F(x)).
DF (p : q) = F(p) − F(q) − hp − q,rF(q)i


Convex duality: Legendre transformation
I For a strictly convex and differentiable function F : X ! R:
F(y) = sup
x2X{hy, xi − F(x) | {z }
lF (y;x);
}
I Maximum obtained for y = rF(x):
rx lF (y; x) = y − rF(x) = 0 ) y = rF(x)
I Maximum unique from convexity of F (r2F 0):
r2x
lF (y; x) = −r2F(x) 0
I Convex conjugates:
(F,X) , (F,Y), Y = {rF(x) | x 2 X}


Legendre duality Canonical divergence
I Convex conjugates have functional inverse gradients
rF−1 = rF
rF may require numerical approximation
(not always available in analytical closed-form)
I Involution: (F) = F.
I Convex conjugate F expressed using (rF)−1:
F(y) = h(rF)−1(y), yi − F((rF)−1(y))
I Fenchel-Young inequality at the heart of canonical divergence:
F(x) + F(y) hx, yi
AF (x : y) = AF(y : x) = F(x) + F(y) − hx, yi 0


Dual Bregman divergences canonical divergence [6]
KL(P : Q) = EP

log
p(x)
q(x)

0
= BF (Q : P) = BF(P : Q)
= F(Q) + F(P) − hQ, Pi
= AF (Q : P) = AF(P : Q)
with Q (natural parameterization) and P = EP[t(X)] = rF(P)
(moment parameterization).


Exponential family mixtures: Dual parameterizations
A finite weighted point set {(wi , i )}ki
=1 in a statistical manifold.
Many coordinate systems for computing (two canonical):
I usual -parameterization,
I natural -parameterization and dual -parameterization.
Original parameters
2
Exponential family
dual parameterization
Legendre transform
(, F) $ (H, F)
2 2 H
= rF() = rF()
Natural parameters Expectation parameters


Maximum Likelihood Estimator (MLE)
Given n identical and independently distributed observations
X = {x1, ..., xn}
Maximum Likelihood Estimator
Yn
ˆ= argmax2
i=1
pF (xi ; ) = argmax2ePn
i=1ht(xi ),i−F()+k(xi )
is unique maximum since r2F 0 (Hessian):
rF(ˆ) =
1
n
Xn
i=1
t(xi )
MLE is consistent, efficient with asymptotic normal distribution
ˆ N

,
1
n

I−1()
Fisher information matrix
I () = var[t(X)] = r2F()
MLE may be biased (eg, normal distributions).

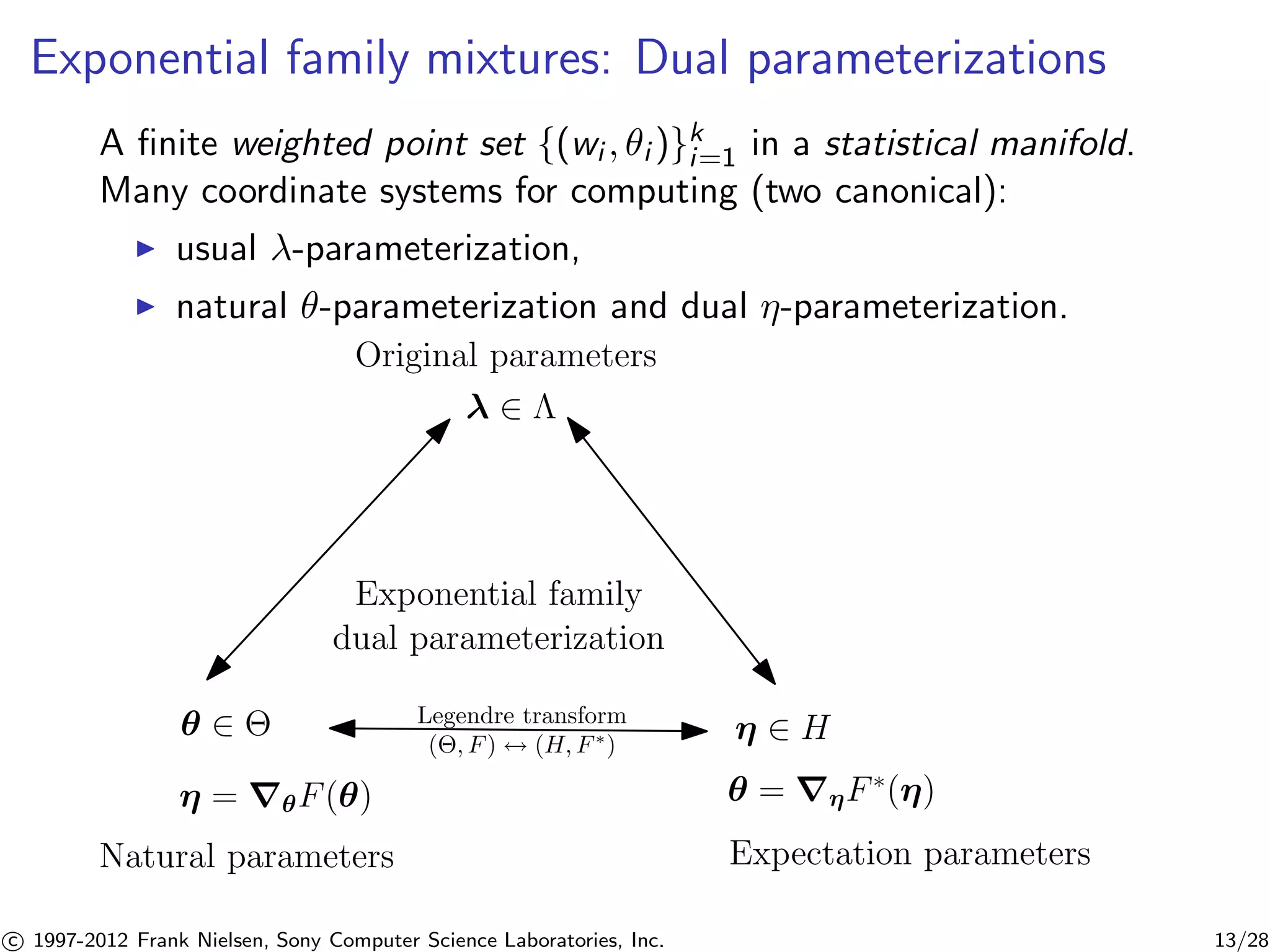
Duality Bregman $ Exponential families [2]
Bregman divergence:
BF (x : )
Bregman generator:
F()
Cumulant function:
F()
Exponential family:
pF (x|)
Legendre
duality
= rF()
An exponential family...
pF (x; ) = exp(ht(x), i − F() + k(x))
has the log-density interpreted as a Bregman divergence:
log pF (x; ) = −BF(t(x) : ) + F(t(x)) + k(x)


Exponential families , Bregman divergences: Examples
F(x) pF (x|) , BF
Generator Exponential Family , Dual Bregman divergence
x2 Spherical Gaussian , Squared loss
x log x Multinomial , Kullback-Leibler divergence
x log x − x Poisson , I -divergence
−log(−2x) Rayleigh , Itakura-Saito divergence
−log x Geometric , Itakura-Saito divergence
log |X| Wishart , log-det/Burg matrix div. [8]


Maximum likelihood estimator revisited
ˆ = argmax
Qn
i=1 pF (xi ; ) = argmax
Pn
i=1 log pF (xi ; )
argmax
Xn
i=1
(ht(xi ), i − F() + k(xi ))
argmax
Xn
i=1
−BF(t(xi ) : ) + F(t(xi )) + k(xi ) | {z }
constant
argmin
Xn
i=1
BF(t(xi ) : )
Right-sided Bregman centroid = center of mass: ˆ = 1
n
Pn
i=1 t(xi ).


Bregman batched Lloyd’s k-means [2]
Extends Lloyd’s k-means heuristic to Bregman divergences.
I Initialize distinct seeds: C1 = P1, ..., Ck = Pk
I Repeat until convergence
I Assign point Pi to its “closest” centroid (wrt. BF (Pi : C))
Ci = {P 2 P | BF (P : Ci ) BF (P : Cj ) 8j6= i}
I Update cluster centroids by taking their center of mass:
Ci = 1
|Ci |
P
P2Ci
P.
Loss function
LF (P : C) =
X
P2P
BF (P : C)
BF (P : C) = min
i2{1,...,k}
BF (P : Ci )
...monotonically decreases and converges to a local optimum.
(Extend to weighted point sets using barycenters.)


k-MLE for EFMM Bregman Hard Clustering [4]
Bijection exponential families (distributions) $ Bregman distances
log pF (x; ) = −BF(t(x) : ) + F(t(x)) + k(x), = rF()
Bregman k-MLE for EFMMs (F) = additively weighted Bregman
hard k-means for F in the Qspace {yi = t(xi )}i :
Complete log-likelihood log
n
i=1
Qk
j=1(wjpF (xi |j ))j (zi ):
= max
,w
Xn
i=1
Xk
j=1
j (zi )(log pF (xi |j ) + log wj )
min
H,w
Xn
i=1
Xk
j=1
j (zi )((BF (t(xi ) : j ) − log wj )−k(xi ) − F(t(xi ) | {z }
constant
)
min
,w
Xn
i=1
k
min
j=1
BF(t(xi ) : j ) − log wj
(This is the argmin that gives the zi ’s)


Complete average log-likelihood optimization
Minimize monotonically the complete average log-likelihood:
1
n
min
H,w
Xn
i=1
k
min
j=1
BF(t(xi ) : j ) − log wj
I 1. Constant weights ! dual additive Bregman k-means
1
n
min
H
Xn
i=1
k
min
j=1
(BF(t(xi ) : j ) − log wj )
I 2. Component moment parameters fixed:
min
w
Xn
i=1
Xk
j=1
−j (zi ) log wj = min
w
Xk
j=1
−j log wj ,
where j = |Cj |
n . That is, minimize the cross-entropy:
minw H×( : w) ) w = .
I Go to 1 until (local) convergence is met.


k-MLE-EFMM algorithm [4]
I 0. Initialization: 8i 2 {1, ..., k}, let wi = 1
k and i = t(xi )
(initialization is further discussed later on).
I 1. Assignment:
8i 2 {1, ..., n}, zi = argminkj
=1BF(t(xi ) : j ) − log wj .
Let Ci = {xj |zj = i}, 8i 2 {1, ..., k} be the cluster partition:
X = [ki
=1Ci .
I 2. Update the -parameters:
P
8i 2 {1, ..., k}, 1
i = |Ci |
x2Ci
t(x).
Goto step 1 unless local convergence of the complete
likelihood is reached.
I 3. Update the mixture weights: 8i 2 {1, ..., k},wi = 1
n |Ci |.
Goto step 1 unless local convergence of the complete
likelihood is reached.


k-MLE initialization
I Forgy’s random seed (d = D),
I Bregman k-means (for F on Y, and MLE on each cluster).
Usually D d (eg., multivariate Gaussians D = d(d+3)
2 )
I Compute global MLE ˆ = 1
n
Pn
i=1 t(xi )
(well-defined for n D ! ˆ 2 )
I Consider restricted exponential family for Fˆ(d+1...D)((1...d)),
i = t(1...d)(xi ) and (d+1...D)
then set (1...d)
i = ˆ(d+1...D).
(e.g., we fix global covariance matrix, and let μi = xi for
Gaussians)
I Improve initialization by applying Bregman k-means++ [1] for
the convex conjugate of Fˆ(d+1...D)((1...d))
k-MLE++ based on Bregman k-means++


k-MLE variants using any Bregman k-means heuristic
I Any k-means optimization heuristic allows one to update the
mixture -parameters.
I Hartigan Wang’s greedy swap (after Lloyd convergence)
I Kanungo et al. swap ((9 + )-approximation)
I Performing successively mixture and w parameters yield
Hard EM variant.
(easily implemented by winner-take-all EM weight
membership)


k-MLE for MVNs with the (μ,) parameters
I 0. Initialization:
I Calculate global mean ¯μ and global covariance matrix ¯
:
¯μ = 1
n
Pk
i=1 xi , ¯
= 1
n
Pk
i=1 xi xT
i − ¯μ¯μT
I 8i 2 {1, ..., k}, initialize the i th seed as (μi = xi ,i = ¯
).
I 1. Assignment: 8i 2 {1, ..., n}
zi = argminkj
=1M−1
i
(x − μi , x − μi ) + log |i | − 2 log wi with
M−1
i
(x − μi , x − μi ) the squared Mahalanobis distance:
MQ(x, y) = (x − y)TQ(x − y). Let
Ci = {xj |zj = i}, 8i 2 {1, ..., k} be the cluster partition:
X = [ki
=1Ci .
I 2. Update the parameters:
P
8i 2 {1, ..., k}, μi = 1
|Ci |
x2Ci
x,i = 1
|Ci |
P
x2Ci
xxT − μiμTi
Goto step 1 unless local convergence.
I 3. Update the mixture weights: 8i 2 {1, ..., k},wi = |Ci |
n .
Goto step 1 unless local convergence.


Summary of contributions
I Hard k-MLE versus soft EM:
I k-MLE maximizes locally the complete likelihood
I EM maximizes the incomplete likelihood
I The component parameter update can be implemented
using any Bregman k-means heuristic on conjugate F,
I Initialization can be performed using k-MLE++
I Indivisibility: Robustness when identifying statistical mixture
models? Which k? 8k 2 N, N(μ, 2) =
Pk
i=1 N

μ
k , 2
k

Simplifying mixtures from kernel density estimators is one
fine-to-coarse solution. See:
Model centroids for the simplification of kernel density
estimators, ICASSP 2012, March 29th.


Marcel R. Ackermann and Johannes Bl¨omer.
Bregman clustering for separable instances.
In Scandinavian Workshop on Algorithm Theory (SWAT),
pages 212–223, 2010.
Arindam Banerjee, Srujana Merugu, Inderjit S. Dhillon, and
Joydeep Ghosh.
Clustering with Bregman divergences.
Journal of Machine Learning Research, 6:1705–1749, 2005.
Vincent Garcia and Frank Nielsen.
Simplification and hierarchical representations of mixtures of
exponential families.
Signal Processing (Elsevier), 90(12):3197–3212, 2010.
Frank Nielsen.
k-MLE: A fast algorithm for learning statistical mixture
models.
In IEEE International Conference on Acoustics, Speech, and
Signal Processing (ICASSP). IEEE, 2012.


preliminary, technical report on arXiv.
Frank Nielsen and Vincent Garcia.
Statistical exponential families: A digest with flash cards,
2009.
arXiv.org:0911.4863.
Frank Nielsen and Richard Nock.
Entropies and cross-entropies of exponential families.
In International Conference on Image Processing (ICIP), pages
3621–3624, 2010.
Jose Seabra, Francesco Ciompi, Oriol Pujol, Josepa Mauri,
Petia Radeva, and Joao Sanchez.
Rayleigh mixture model for plaque characterization in
intravascular ultrasound.
IEEE Transaction on Biomedical Engineering,
58(5):1314–1324, 2011.
Shijun Wang and Rong Jin.


An information geometry approach for distance metric
learning.
Journal of Machine Learning Research, 5:591–598, 2009.


Anisotropic Voronoi diagram (for MVN MMs)
From the source color image (a), we buid a 5D GMM with k = 32
components, and color each pixel with the mean color of the
anisotropic Voronoi cell it belongs to
(a) (b)
Speed-up assignment step using Bregman ball trees or Bregman
vantage point trees.


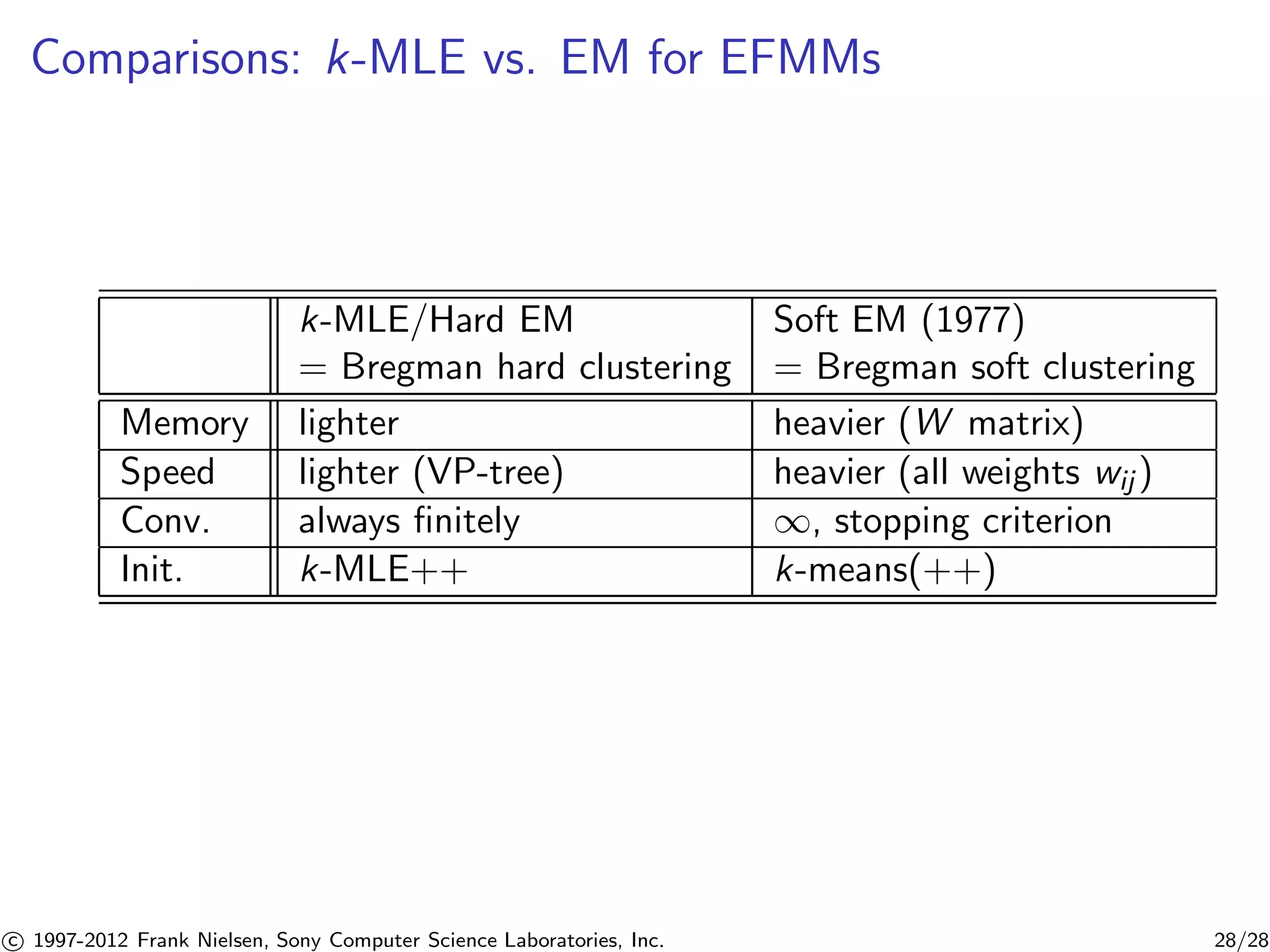
Expectation-maximization (EM) for EFMMs [2]
EM increases monotonically the expected complete likelihood
(marginalize):
Xn
i=1
Xk
j=1
p(zj |xi , ) log p(xi , zj |)
Banerjee et al. [2] proved it amounts to a Bregman soft clustering:


Comparisons: k-MLE vs. EM for EFMMs
k-MLE/Hard EM Soft EM (1977)
= Bregman hard clustering = Bregman soft clustering
Memory lighter heavier (W matrix)
Speed lighter (VP-tree) heavier (all weights wij )
Conv. always finitely 1, stopping criterion
Init. k-MLE++ k-means(++)


k-MLE: A fast algorithm for learning statistical mixture models

More Related Content

What's hot

Viewers also liked

Similar to k-MLE: A fast algorithm for learning statistical mixture models

Recently uploaded

k-MLE: A fast algorithm for learning statistical mixture models