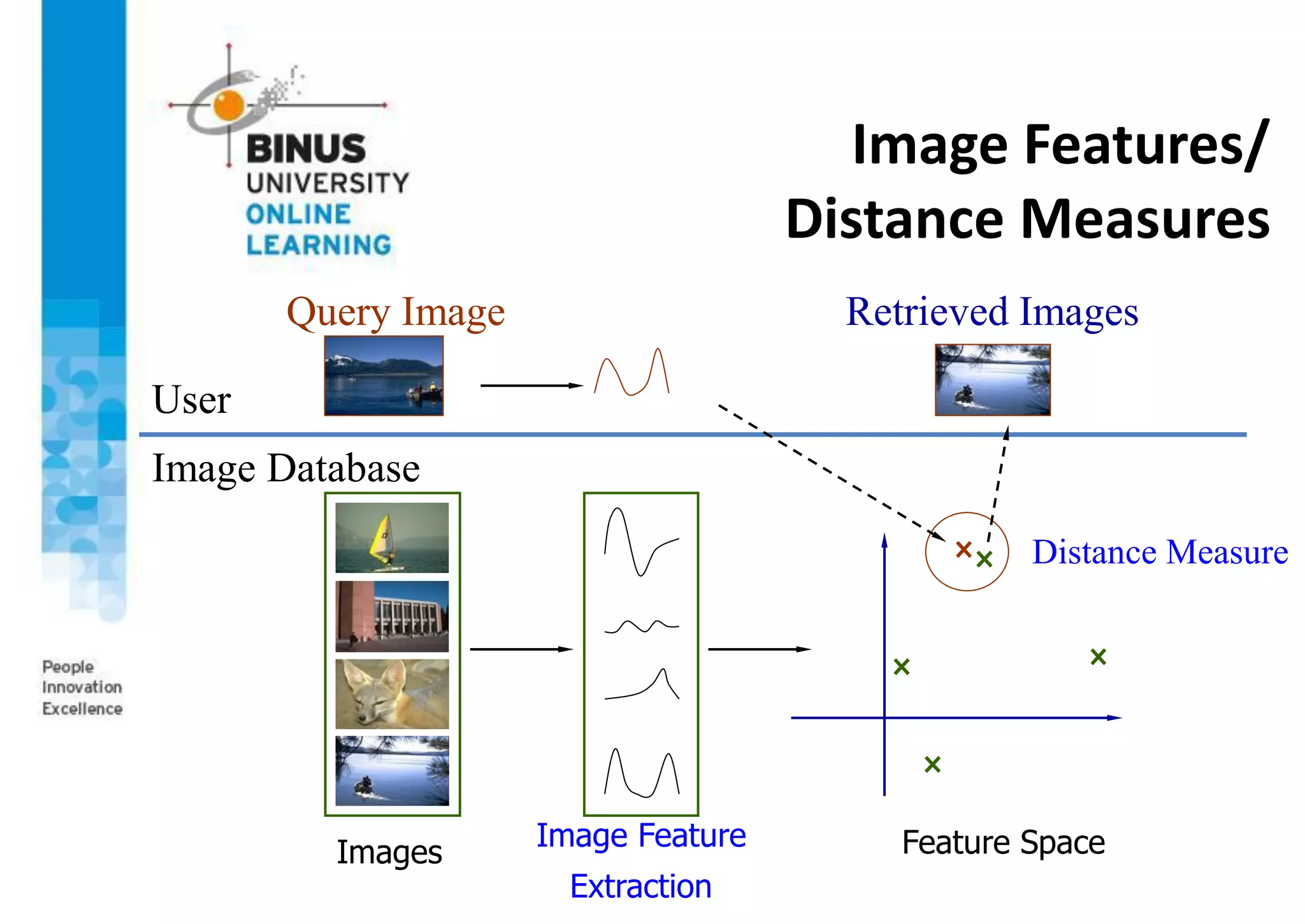
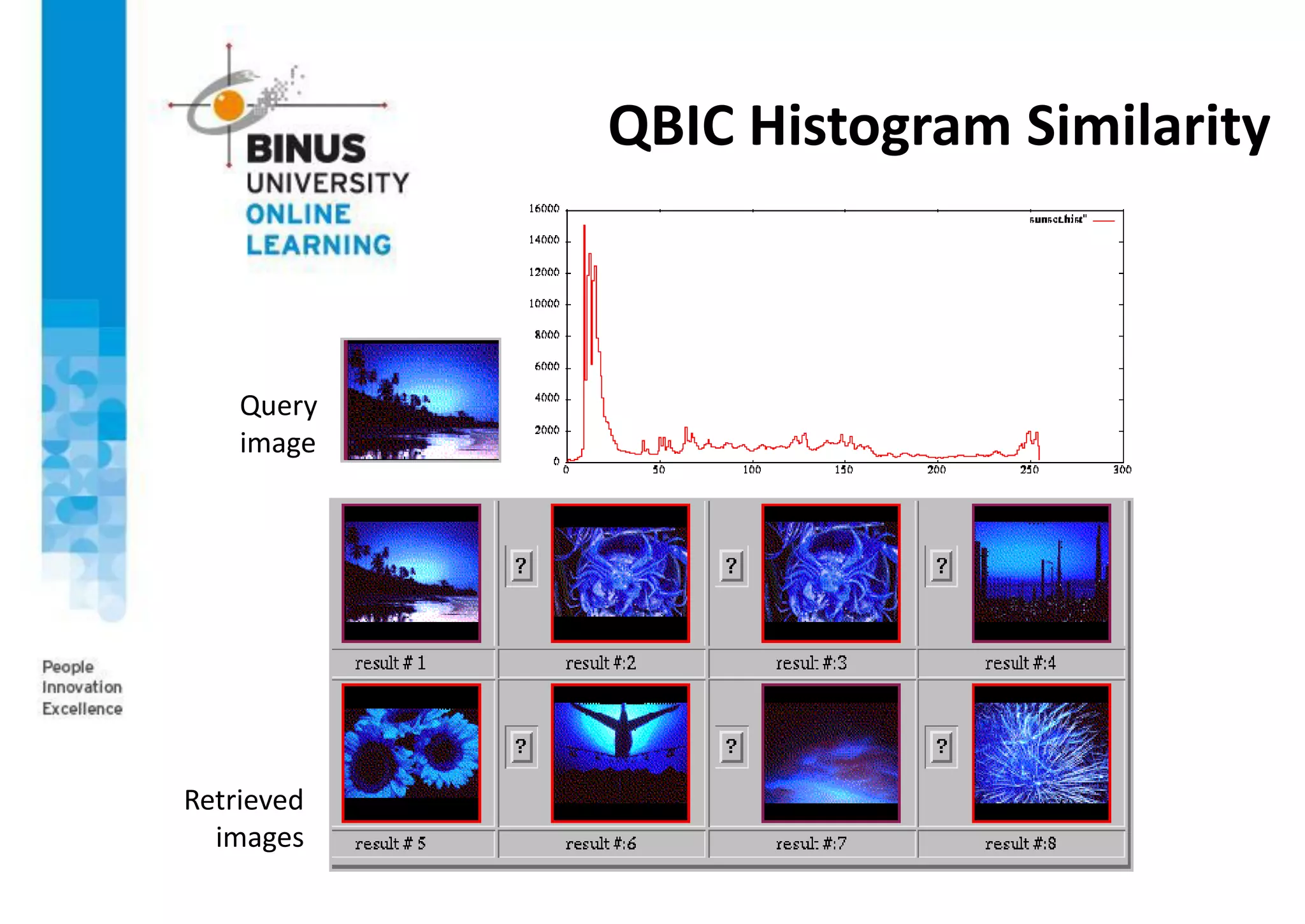
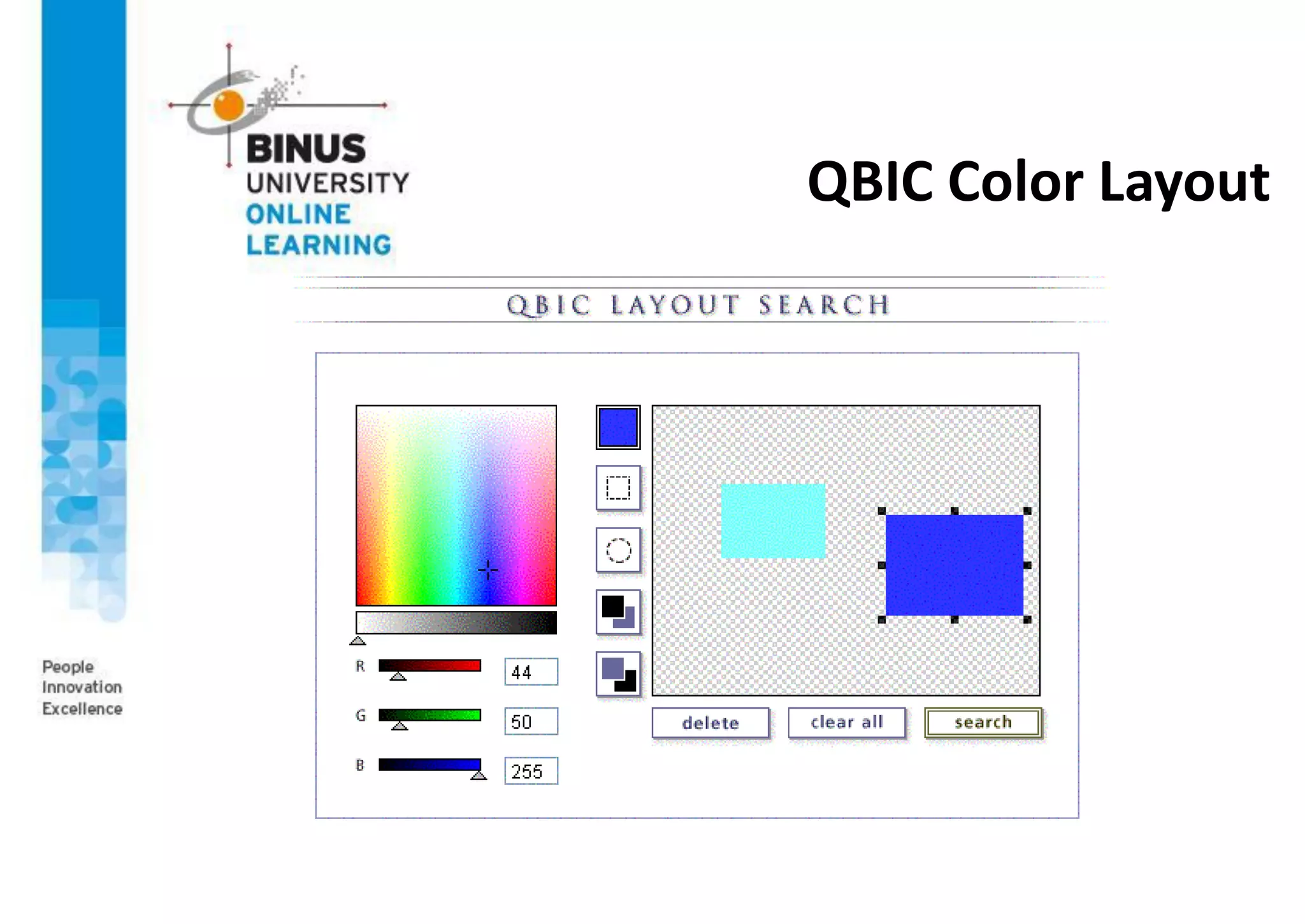
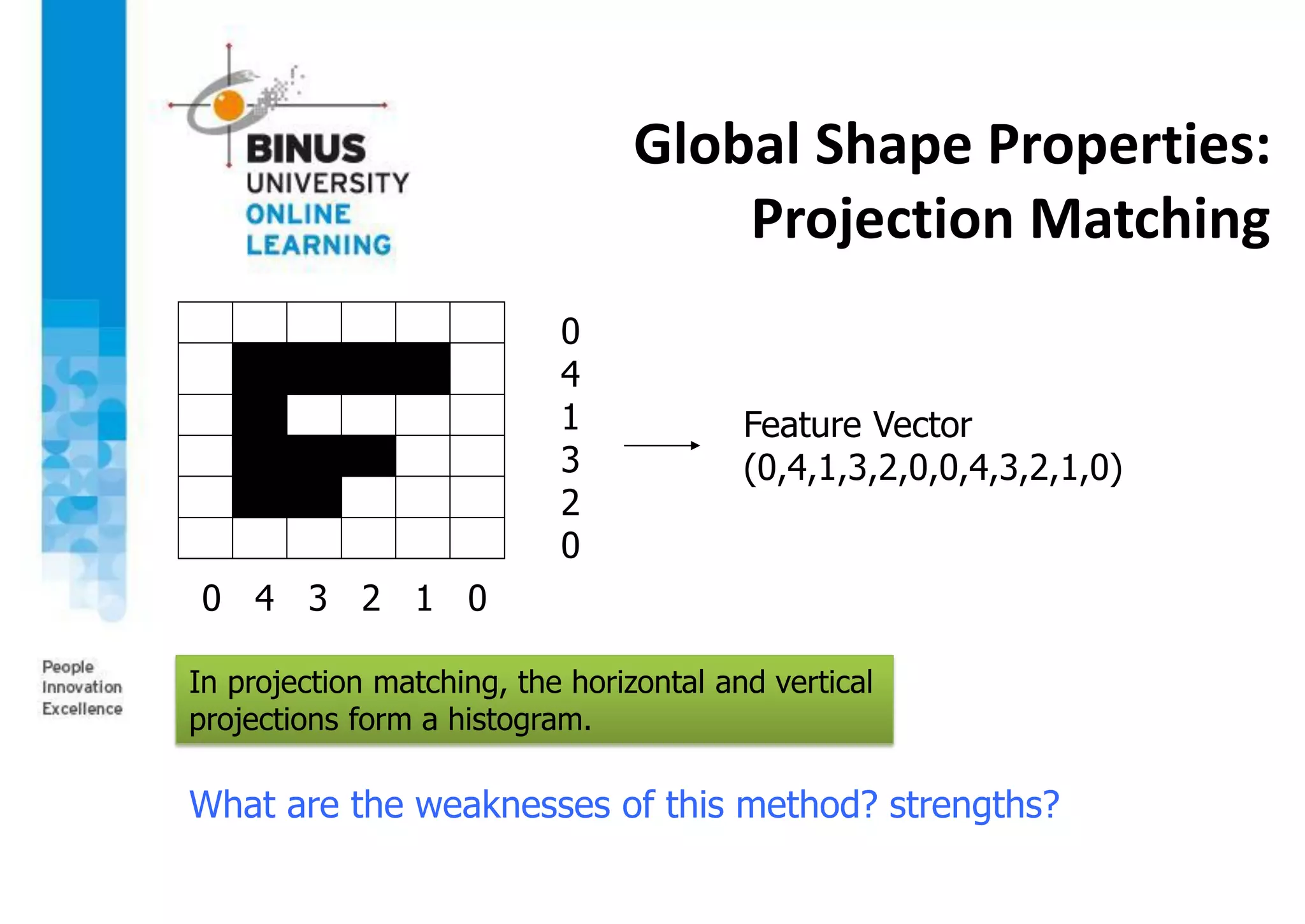
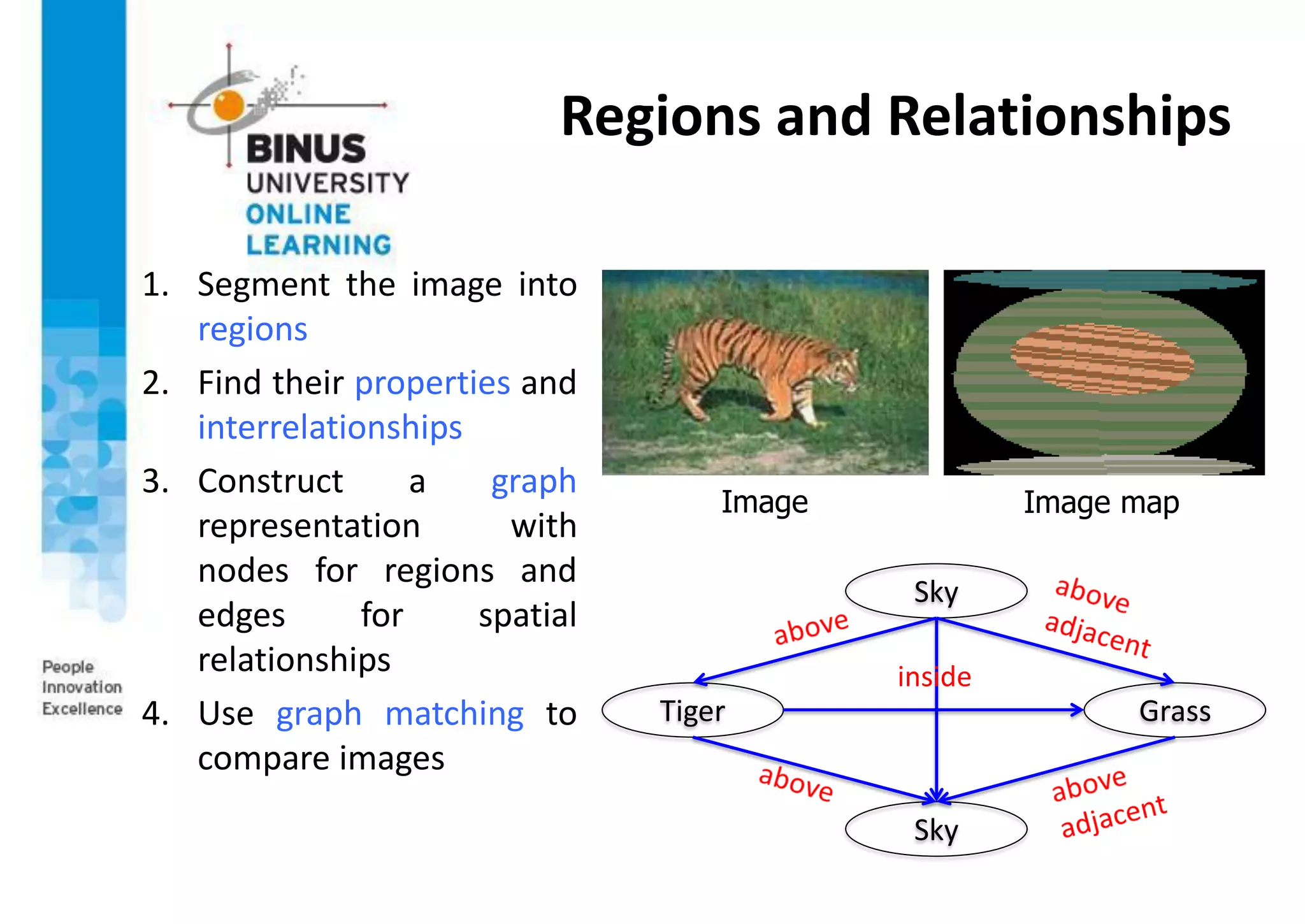
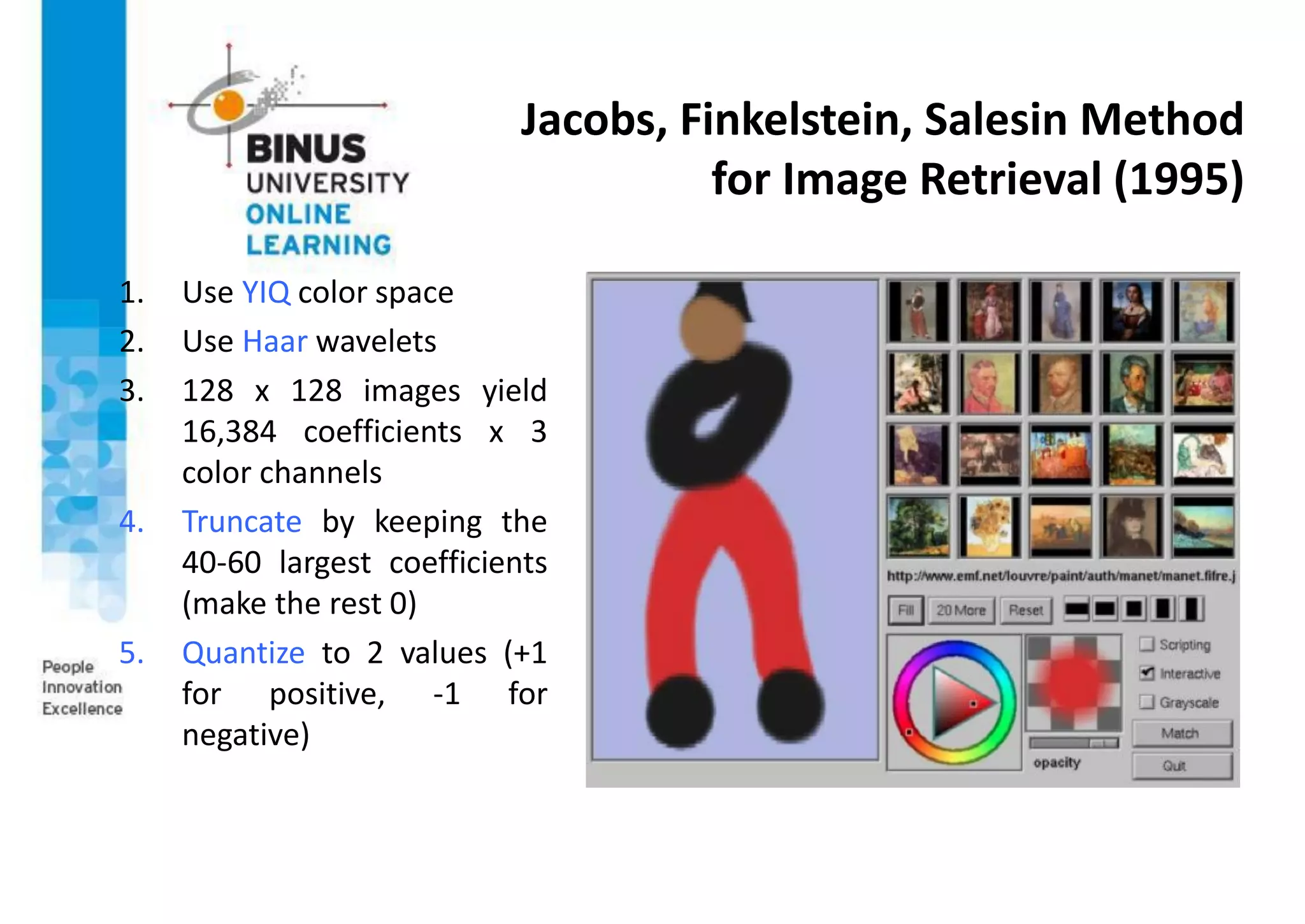
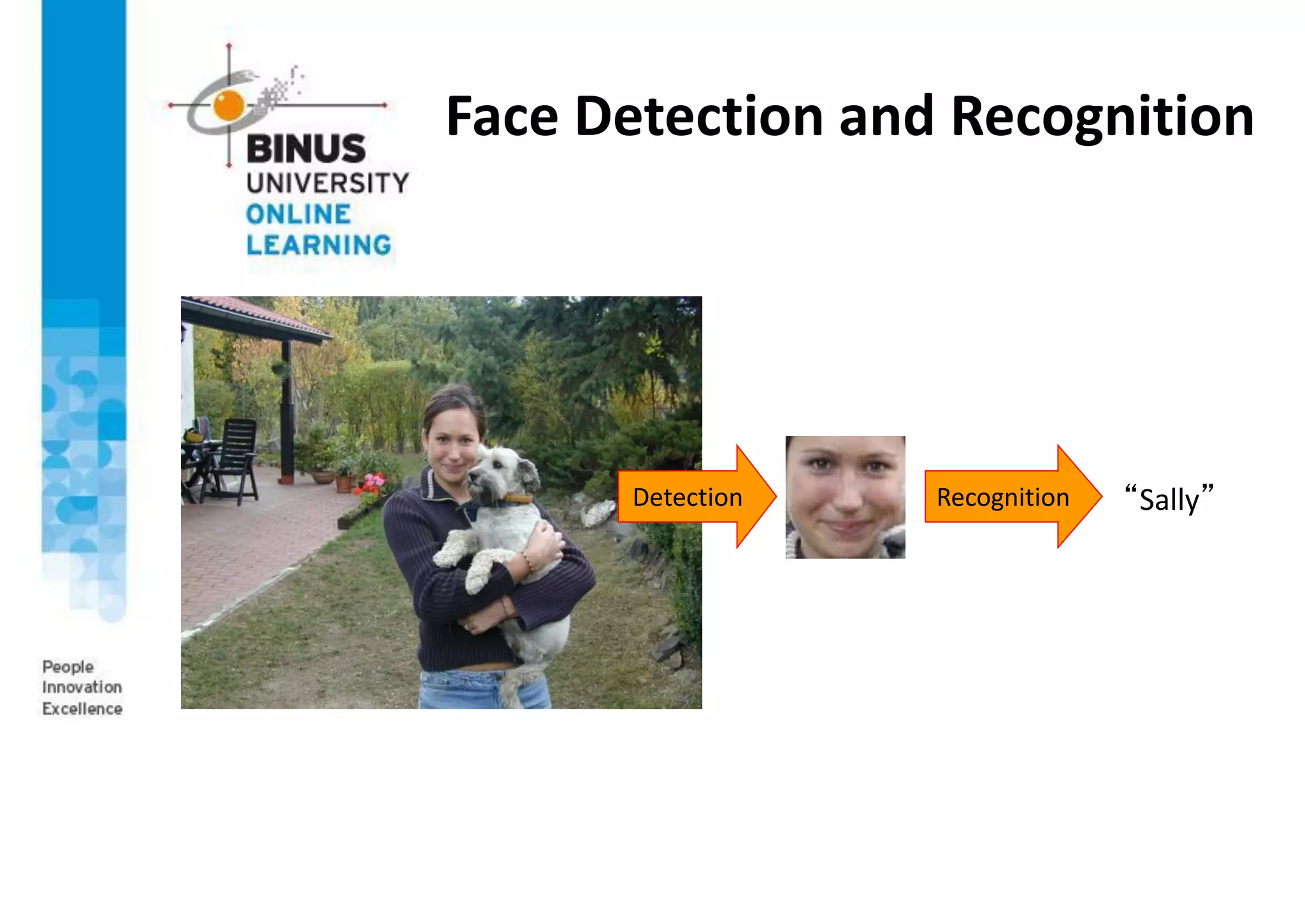
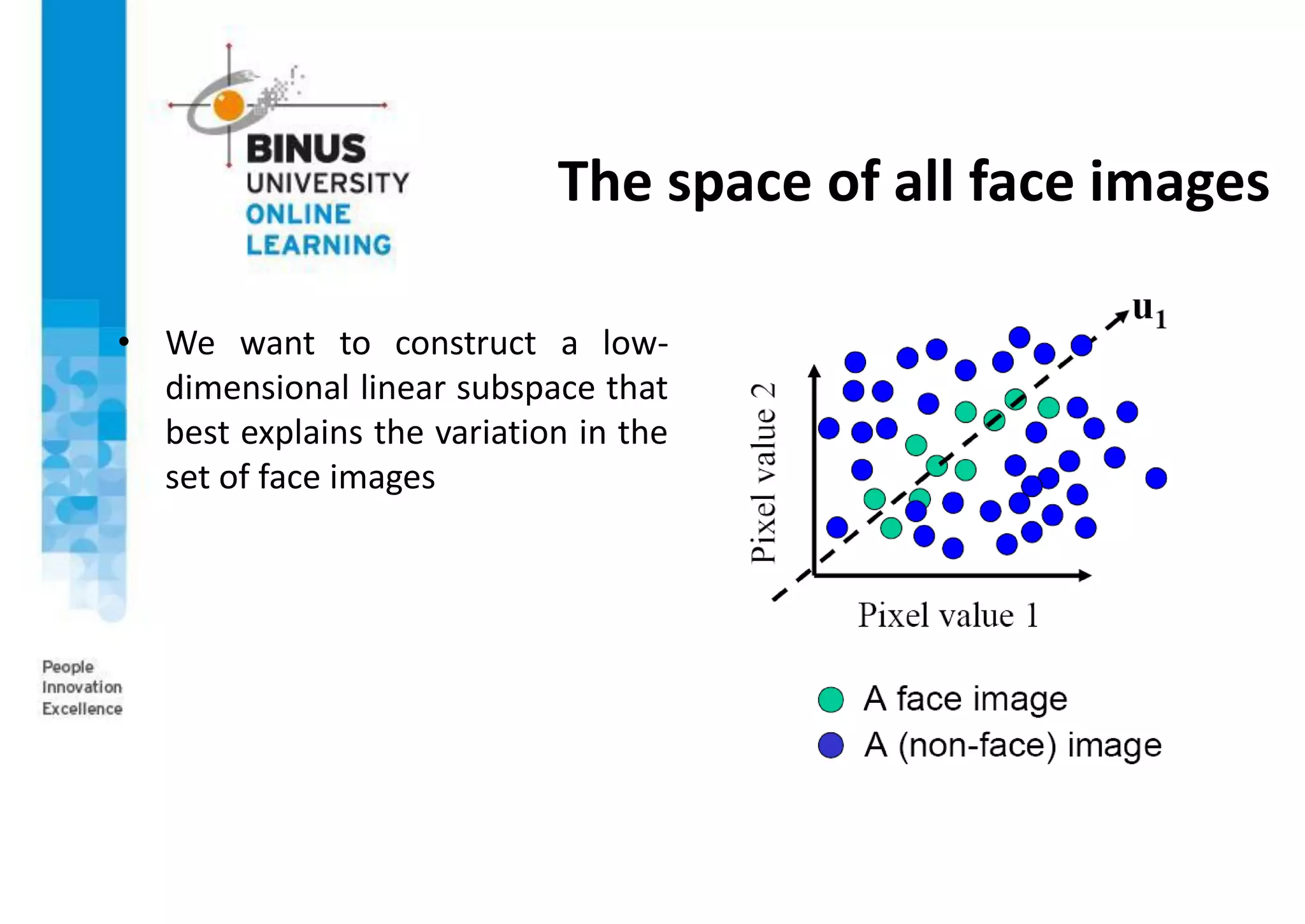
This document provides an overview of machine vision applications including content-based image retrieval and face recognition. It discusses how content-based image retrieval systems work by extracting image features, calculating distances between images, and returning similar images from a database based on a query image. Examples of content-based image retrieval systems and the features they use are described. The document also covers face detection and recognition techniques, including the use of eigenfaces which represent faces as locations in a lower-dimensional space.

1. Course: Machine Vision
Sample Applications
Session 13
D5627 – I Gede Putra Kusuma Negara, B.Eng., PhD

2. Outline
• Content Based Image Retrieval
• Face Recognition

3. Content Based Image Retrieval

4. Content-based Image Retrieval
(CBIR)
Searching a large database for images that match a query:
• What kinds of databases?
• What kinds of queries?
• What constitutes a match?
• How do we make such searches efficient?

5. Applications
• Art Collections
– e.g. Fine Arts Museum of San Francisco
• Medical Image Databases
– CT, MRI, Ultrasound, The Visible Human
• Scientific Databases
– e.g. Earth Sciences
• General Image Collections for Licensing
– Corbis, Getty Images
• The World Wide Web

6. What is a Query?
An image you already have
– How did you get it?
A rough sketch you draw
– How might you draw it?
A symbolic description of what you want
– What’s an example?

7. Example: IBM QBIC
• IBM QBIC (Query by Image
Content)
• The first commercial system
• Uses or has-used color
percentages, color layout,
texture, shape, location, and
keywords.

8. Example: Berkeley Blobworld
• Images are segmented on
color plus texture
• User selects a region of the
query image
• System returns images with
similar regions
• Works really well for tigers
and zebras

9. Example: Like.com
• Small company
• Search for products similar to a
selected one
• Purses, shoes, sunglasses,
jewelry…etc.

10. Image Features/
Distance Measures
Image Database
Query Image
Distance Measure
Retrieved Images
Image Feature
Extraction
User
Feature Space
Images

11. Features
• Color
histograms, gridded layout, wavelets
• Texture
Laws, Gabor filters, LBP, polarity
• Shape
What preprocessing must occur to get shape?
• Objects and their Relationships
This is the most powerful, but you have to be able to recognize the
objects!

12. QBIC Histogram Similarity
• h(I) is a K-bin histogram of a database image
• h(Q) is a K-bin histogram of the query image
• The QBIC color histogram distance is:
• A is a K x K similarity matrix
dhist =(I,Q)=(h(I)-h(Q))A(h(I)-h(Q))
R G B Y C V
1 0 0 .5 0 .5
0 1 0 .5 .5 0
0 0 1
1
1
1
R
G
B
Y
C
V
?
?

13. QBIC Histogram Similarity
Query
image
Retrieved
images

14. Gridded Color
• Gridded color distance is the sum of the color distances
• in each of the corresponding grid squares.
What color distance would you use for a pair of grid squares?
1 1
2 2
3 3
4 4

15. QBIC Color Layout

16. Search by Texture
• Pick and Click (user clicks on a pixel and system
– retrieves images that have in them a region with
– similar texture to the region surrounding it
• Gridded (just like gridded color, but use texture)
• Histogram-based (e.g. compare the LBP histograms)

17. Laws Texture
Query image
Retrieval result using color histogram
and Laws texture feature

18. Shape Distances
• Shape goes one step further than color and texture.
• It requires identification of regions to compare.
• There have been many shape similarity measures suggested for
pattern recognition that can be used to construct shape distance
measures.

19. Global Shape Properties:
Projection Matching
0
4
1
3
2
0
0 4 3 2 1 0
In projection matching, the horizontal and vertical
projections form a histogram.
Feature Vector
(0,4,1,3,2,0,0,4,3,2,1,0)
What are the weaknesses of this method? strengths?

20. Global Shape Properties:
Line-Angle Histograms
Is this feature invariant to starting point?
Is it invariant to size, translation, rotation?

21. Boundary Matching
• Fourier Descriptors
• Sides and Angles
• Elastic Matching
• The distance between query shape and image shape has
two components:
1. energy required to deform the query shape into one that best
matches the image shape
2. measure of how well the deformed query matches the image

22. Del Bimbo Elastic Shape
Matching
query retrieved images

23. Regions and Relationships
1. Segment the image into
regions
2. Find their properties and
interrelationships
3. Construct a graph
representation with
nodes for regions and
edges for spatial
relationships
4. Use graph matching to
compare images
Sky
Tiger Grass
Sky
inside
Image Image map

24. Object Detection:
Rowley’s Face Finder
1. Convert to gray scale
2. Normalize for lighting*
3. Histogram equalization
4. Apply neural net(s) trained
on 16K images
• What data is fed to the
classifier?
• 32 x 32 windows in a
pyramid structure

25. Fleck and Forsyth’s
Skin Detector
• The “Finding Naked People” Paper
• Algorithm:
• Look for LARGE areas that satisfy this to identify pornography.
1. Convert RGB to HIS
2. Use the intensity component to compute a texture map
texture = med2 ( | I - med1(I) | )
3. If a pixel falls into either of the following ranges, it’s a
potential skin pixel
texture < 5, 110 < hue < 150, 20 < saturation < 60
texture < 5, 130 < hue < 170, 30 < saturation < 130

26. Skin Detector
Input image Detected skin area
(in black)

27. Jacobs, Finkelstein, Salesin Method
for Image Retrieval (1995)
1. Use YIQ color space
2. Use Haar wavelets
3. 128 x 128 images yield
16,384 coefficients x 3
color channels
4. Truncate by keeping the
40-60 largest coefficients
(make the rest 0)
5. Quantize to 2 values (+1
for positive, -1 for
negative)

28. Andy Berman’s FIDS System
• Multiple distance
measures
• Boolean and linear
combinations
• Efficient indexing using
images as keys

29. Bare-Bones Triangle Inequality
Algorithm
Offline
1. Choose a small set of key images
2. Store distances from database
images to keys
Online (given query Q)
1. Compute the distance from Q to
each key
2. Obtain lower bounds on distances
to database images
3. Threshold or return all images in
order of lower bounds
Offline
1. Choose key images for each
measure*)
2. Store distances from database
images to keys for all measures
Online (given query Q)
1. Calculate lower bounds for each
measure
2. Combine to form lower bounds for
composite measures
3. Continue as in single measure
algorithm
*) with multiple distance measure

30. Face Recognition

31. Face Detection and Recognition
Detection Recognition “Sally”

32. History
• Early face recognition systems: based on features and
distances
Bledsoe (1966), Kanade (1973)
• Appearance-based models: eigenfaces
Sirovich & Kirby (1987), Turk & Pentland (1991)
• Real-time face detection with boosting
Viola & Jones (2001)

33. The space of all face images
• When viewed as vectors of pixel
values, face images are
extremely high-dimensional
• 100x100 image = 10,000
dimensions
• However, relatively few 10,000-
dimensional vectors correspond
to valid face images
• We want to effectively model the
subspace of face images

34. The space of all face images
• We want to construct a low-
dimensional linear subspace that
best explains the variation in the
set of face images

35. Principal Component Analysis
• Given: N data points x1, … ,xN in Rd
• We want to find a new set of features that are linear
combinations of original ones:
u(xi) = uT(xi – µ)
(µ: mean of data points)
• What unit vector u in Rd captures the most variance of the
data?

36. Principal Component Analysis
• Direction that maximizes the variance of the projected
data:
• Direction that maximizes the variance is the eigenvector
associated with the largest eigenvalue of Σ
var(u) =
1
N
uT
(xi -m)
i=1
N
å (uT
(xi -m))T
= uT
(xi -m)
i=1
N
å (xi -m)T
é
ë
ê
ù
û
úu
= uT
u
å
Projection of data point
Covariance matrix

37. Eigenfaces: Key idea
• Assume that most face images lie on
a low-dimensional subspace determined by the first k (k<d)
directions of maximum variance
• Use PCA to determine the vectors u1,…uk that span that
subspace:
x ≈ μ + w1u1 + w2u2 + … + wkuk
• Represent each face using its “face space” coordinates
(w1,…wk)
• Perform nearest-neighbor recognition in “face space”

38. Eigenfaces example
Training images x1,…,xN

39. Eigenfaces example
Top eigenvectors:
u1,…uk
Mean: μ

40. Eigenfaces example
Face x in “face space” coordinates:
Reconstruction:
= +
µ + w1u1 + w2u2 + w3u3 + w4u4 + …
^
x =
x [u1
T
(x -m),...,uk
T
(x -m)]
= w1,w2,...,wk

41. Summary: Recognition with
Eigenfaces
Process labeled training images:
• Find mean µ and covariance matrix Σ
• Find k principal components (eigenvectors of Σ) u1,…uk
• Project each training image xi onto subspace spanned by principal
components:
(wi1,…,wik) = (u1
T(xi – µ), … , uk
T(xi – µ))
Given novel image x:
• Project onto subspace:
(w1,…,wk) = (u1
T(x– µ), … , uk
T(x – µ))
• Optional: check reconstruction error x – x to determine whether
image is really a face
• Classify as closest training face in k-dimensional subspace
^

42. Acknowledgment
Some of slides in this PowerPoint presentation are adaptation from
various slides, many thanks to:
1. Linda Saphiro, Department of Computer Science and Engineering,
University of Washington
(http://homes.cs.washington.edu/~shapiro/)
2. Svetlana Lazebnik, Department of Computer Science, University of
Illinois at Urbana-Champaign (http://web.engr.illinois.edu/~slazebni/)

43. Thank You