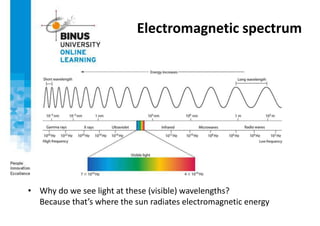
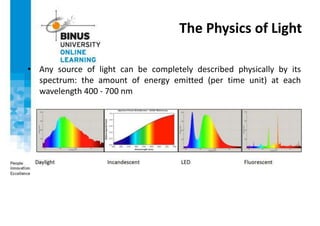
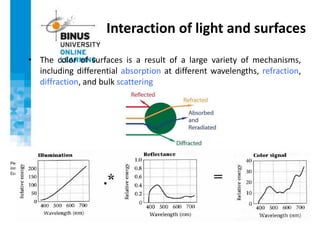
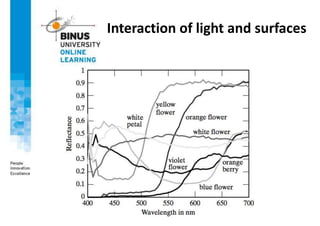
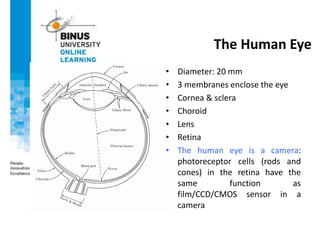
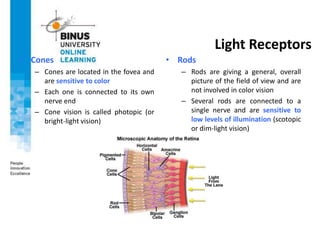
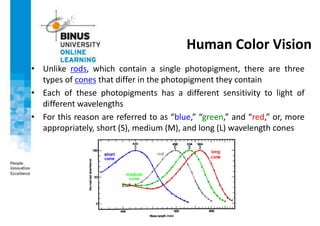
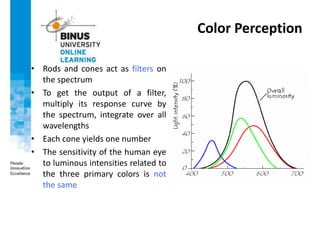
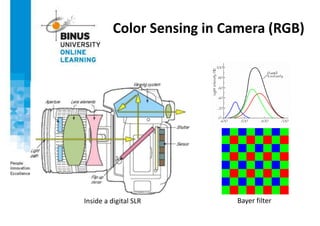
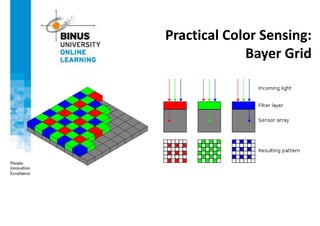
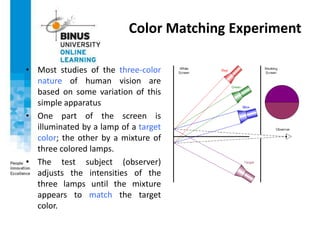
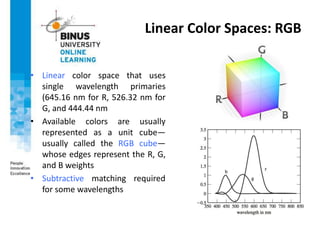
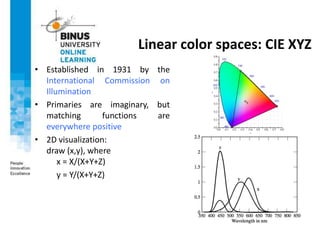
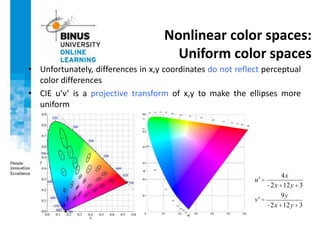
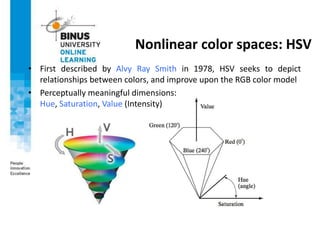
This document provides an overview of light, color, and human color perception. It discusses that color is a psychological property resulting from light interacting with our visual system. The physics of light is described in terms of wavelength. Human color vision involves three types of cones that differ in photopigment sensitivity. Color can be represented using models like RGB, CIE XYZ, and HSV. Computer vision applications make use of color through techniques like color histograms, skin detection, and image segmentation.

1. Course: Machine Vision
Light and Color
Session 03
D5627 – I Gede Putra Kusuma Negara, B.Eng., PhD

2. Outline
• The Physics of Color
• Human Color Perception
• Representing Color
• A Model of Image Color

3. The Physics of Color

4. What is color?
• Color is a psychological property of our visual experiences when we
look at objects and lights, not a physical property of those objects or
lights (S. Palmer, Vision Science: Photons to Phenomenology)
• Color is the result of interaction between physical light in the
environment and our visual system

5. Electromagnetic spectrum
• Why do we see light at these (visible) wavelengths?
Because that’s where the sun radiates electromagnetic energy

6. The Physics of Light
• Any source of light can be completely described physically by its
spectrum: the amount of energy emitted (per time unit) at each
wavelength 400 - 700 nm

7. Interaction of light and surfaces
• The color of surfaces is a result of a large variety of mechanisms,
including differential absorption at different wavelengths, refraction,
diffraction, and bulk scattering

8. Interaction of light and surfaces

9. Human Color Perception

10. The Human Eye
• Diameter: 20 mm
• 3 membranes enclose the eye
• Cornea & sclera
• Choroid
• Lens
• Retina
• The human eye is a camera:
photoreceptor cells (rods and
cones) in the retina have the
same function as
film/CCD/CMOS sensor in a
camera

11. Light Receptors
• Cones
– Cones are located in the fovea and
are sensitive to color
– Each one is connected to its own
nerve end
– Cone vision is called photopic (or
bright-light vision)
• Rods
– Rods are giving a general, overall
picture of the field of view and are
not involved in color vision
– Several rods are connected to a
single nerve and are sensitive to
low levels of illumination (scotopic
or dim-light vision)

12. Human Color Vision
• Unlike rods, which contain a single photopigment, there are three
types of cones that differ in the photopigment they contain
• Each of these photopigments has a different sensitivity to light of
different wavelengths
• For this reason are referred to as “blue,” “green,” and “red,” or, more
appropriately, short (S), medium (M), and long (L) wavelength cones

13. Color Perception
• Rods and cones act as filters on
the spectrum
• To get the output of a filter,
multiply its response curve by
the spectrum, integrate over all
wavelengths
• Each cone yields one number
• The sensitivity of the human eye
to luminous intensities related to
the three primary colors is not
the same

14. Color Sensing in Camera (RGB)
Bayer filter
Inside a digital SLR

15. Practical Color Sensing:
Bayer Grid

16. Representing Color

17. Standardizing color experience
• Accurate color reproduction is
commercially valuable
• Many products are identified by
color (e.g. “golden” arches)
• Only few color names are widely
recognized by English speakers:
– About 10; other languages have
fewer/more, but not many more.
– It’s common to disagree on
appropriate color names.
• Color reproduction problems
increased by prevalence of
digital imaging

18. Color Matching Experiment
• Most studies of the three-color
nature of human vision are
based on some variation of this
simple apparatus
• One part of the screen is
illuminated by a lamp of a target
color; the other by a mixture of
three colored lamps.
• The test subject (observer)
adjusts the intensities of the
three lamps until the mixture
appears to match the target
color.

19. Trichromacy
• Three numbers seem to be sufficient for encoding color
• In color matching experiments, most people can match any given light
with three primaries
• Exception: color blindness
• For the same light and same primaries, most people select the same
weights
• Trichromatic color theory dates back to 18th century (Thomas Young)

20. Additive vs. Subtractive
Color Matching
Additive
• Many colors can be represented
as a mixture of A, B, C:
M=a A + b B + c C
• Where the = sign should be read
as “matches”
• Gives a color description system:
two people who agree on A, B, C
need only supply (a, b, c) to
describe a color
Subtractive
• Some colors can’t be matched
like this M=a A + b B + c C,
instead, must write:
M+a A = b B+c C
• Interpret this as (-a, b, c)
• Problem for building monitors:
Choose R, G, B such that
positive linear combinations
match a large set of colors

21. Grassman’s Laws
• Additive matching is linear
• If two test lights can be matched with the same set of
weights, then they match each other:
– Suppose A = u1 P1 + u2 P2 + u3 P3 and B = u1 P1 + u2 P2 + u3 P3.
Then A = B.
• If we mix two test lights, then mixing the matches will
match the result:
– Suppose A = u1 P1 + u2 P2 + u3 P3 and B = v1 P1 + v2 P2 + v3 P3.
Then A+B = (u1+v1) P1 + (u2+v2) P2 + (u3+v3) P3.
• If we scale the test light, then the matches get scaled
by the same amount:
– Suppose A = u1 P1 + u2 P2 + u3 P3.
Then kA = (ku1) P1 + (ku2) P2 + (ku3) P3.

22. Color Matching Functions
• Choose primaries, say A, B, C
• Given energy function, E(λ) what amounts of primaries will match it?
• For each wavelength, determine how much of A, of B, and of C is
needed to match light of that wavelength alone
a(λ)
b(λ)
c(λ)
• These are color matching functions
• Then the match is
a(l)E(l)dl
ò
{ }A+
b(l)E(l)dl
ò
{ }B+
c(l)E(l)dl
ò
{ }C

23. Linear Color Spaces: RGB
• Linear color space that uses
single wavelength primaries
(645.16 nm for R, 526.32 nm for
G, and 444.44 nm
• Available colors are usually
represented as a unit cube—
usually called the RGB cube—
whose edges represent the R, G,
and B weights
• Subtractive matching required
for some wavelengths

24. Linear color spaces: CIE XYZ
• Established in 1931 by the
International Commission on
Illumination
• Primaries are imaginary, but
matching functions are
everywhere positive
• 2D visualization:
draw (x,y), where
x = X/(X+Y+Z)
y = Y/(X+Y+Z)

25. Nonlinear color spaces:
Uniform color spaces
• Unfortunately, differences in x,y coordinates do not reflect perceptual
color differences
• CIE u’v’ is a projective transform of x,y to make the ellipses more
uniform
u' =
4x
-2x +12y+3
v' =
9y
-2x +12y+3

26. Nonlinear color spaces: HSV
• First described by Alvy Ray Smith in 1978, HSV seeks to depict
relationships between colors, and improve upon the RGB color model
• Perceptually meaningful dimensions:
Hue, Saturation, Value (Intensity)

27. A Model of Image Color

28. The Use of Color
in Computer Vision
• Color histogram for indexing and retrieval
Swain and Ballard, Color Indexing, IJCV 1991
• Skin detection
M. Jones and J. Rehg, Statistical Color Models with Application to
Skin Detection, IJCV 2002
• Image segmentation and retrieval
C. Carson, S. Belongie, H. Greenspan, and Ji. Malik, Blobworld:
Image segmentation using Expectation-Maximization and its
application to image querying, ICVIS 1999
• Robot soccer
M. Sridharan and P. Stone, Towards Eliminating Manual Color
Calibration at RoboCup. RoboCup-2005: Robot Soccer World Cup
IX, Springer Verlag, 2006

29. Acknowledgment
Some of slides in this PowerPoint presentation are adaptation from
various slides, many thanks to:
1. D.A. Forsyth, Department of Computer Science, University of Illinois
at Urbana – Champaign (http://luthuli.cs.uiuc.edu/~daf/)
2. Professor William Hoff, Department of Electrical Engineering &
Computer Science (http://inside.mines.edu/~whoff/)
3. James Hays, Computer Science Department, Brown University,
(http://cs.brown.edu/~hays/)

30. Thank You