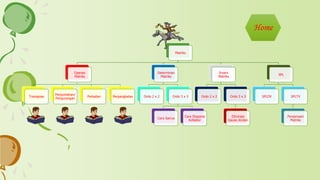
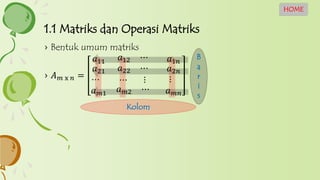
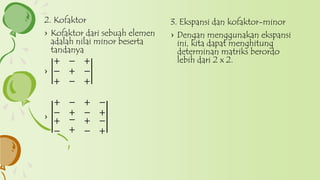
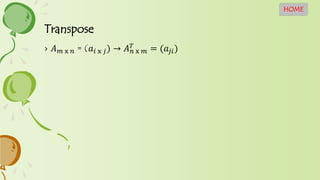Dokumen tersebut memberikan penjelasan tentang konsep dasar matriks, operasi-operasi pada matriks seperti penjumlahan, pengurangan, perkalian, perpangkatan, dan transpose. Juga dibahas tentang determinan matriks, invers matriks, dan penyelesaian sistem persamaan linear menggunakan determinan dan eliminasi Gauss-Jordan.