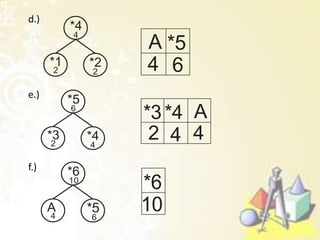
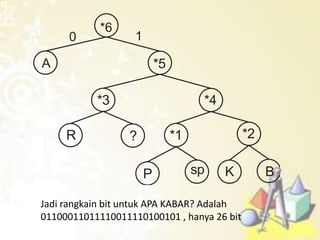
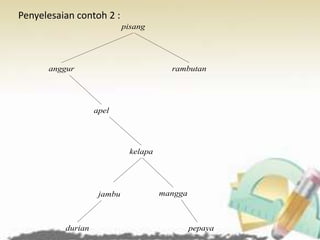
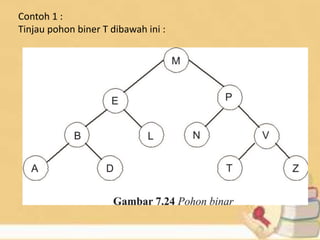
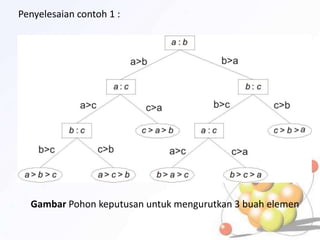
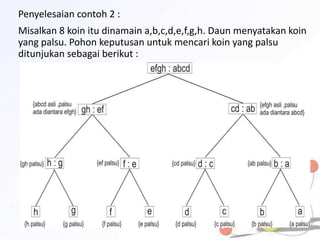
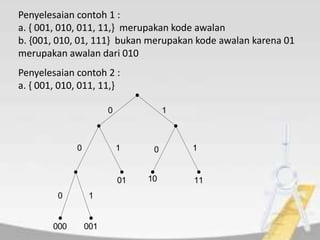
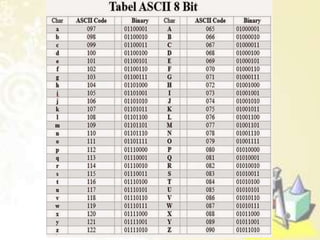
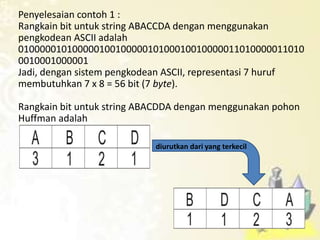
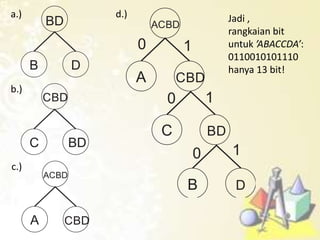
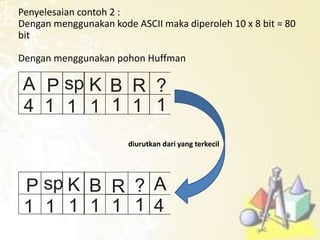
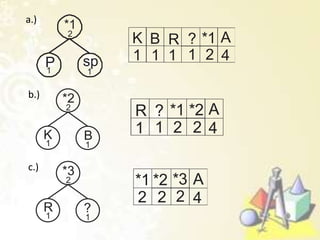
Dokumen tersebut membahas beberapa topik tentang struktur data pohon yang meliputi: 1) Pohon keputusan untuk memecahkan masalah berbasis keputusan, 2) Kode awalan dan kode Huffman untuk kompresi data, 3) Pohon pencarian untuk mencari data, dan 4) Jenis-jenis traversal pada pohon biner seperti preorder, inorder, dan postorder.

1. Siti Eliyah
1714500065
Ulfa Nur A.
1714500067
Wahyu Ageng L.
1714500068
POHON KEPUTUSAN, KODE AWALAN, KODE HUFFMAN,
POHON PENCARIAN & TRANSVERSAL POHON BINER
Kelompok 6
PMtk 5C

2. 1. Pohon Keputusan
• Pohon Keputusan digunakan untuk memodelkan persoalan
yang terdiri dari serangkaian keputusan yang mengarah kesolusi.
• Tiap simpul menyatakan keputusan
• Daun menyatakan solusi
Contoh 1 :
Urutkan tiga buah bilangan a,b, dan c.
Contoh 2 :
Diketahui 8 buah koin uang logam. Satu dari delapan koin itu
ternyata palsu. Koin yang palsu mungkin lebih ringan atau lebih
berat daripada koin yang asli. Misalkan tersedia sebuah
timbangan neraca yang sangat teliti. Buatlah pohon keputusan
untuk mencari uang palsu dengan cara menimbang paling
banyak hanya 3 kali saja.

3. Penyelesaian contoh 1 :
Gambar Pohon keputusan untuk mengurutkan 3 buah elemen

4. Penyelesaian contoh 2 :
Misalkan 8 koin itu dinamain a,b,c,d,e,f,g,h. Daun menyatakan koin
yang palsu. Pohon keputusan untuk mencari koin yang palsu
ditunjukan sebagai berikut :

5. 2. Kode Awalan (prefix code)
• adalah himpunan kode (misalnya kode biner) sedemikian
sehingga tidak ada anggota kumpulan yang merupakan awalan
dari anggota yang lain.
• mempunyai pohon biner yang bersesuain.
• Sisi di beri label 0 atau 1. Pelabelan sisi harus taat-asas, yakni
sisi kiri diberi label 0 saja (atau 1 saja) , sedangkan sisi kanan diberi
label 1 saja (atau 0 saja).
• barisan sisi yang di lalui oleh lintasan dari akar ke daun
menyatakan kode awalan. Kode awalan ini di tulis pada daun.
• Kegunaan untuk :
a. Mengirim pesan pada komunikasi data
b. Untuk pembentukan kode Huffman dalam pemapatan data

6. Contoh 1 :
Apakah himpunan kode biner dibawah ini merupakan kode
awalan? Jika bukan berikan alasanya !
a. { 001, 010, 011, 11,}
b. {001, 010, 01, 111}
Contoh 2 :
Buatlah pohon biner dari kode awalan pada contoh 1

7. Penyelesaian contoh 1 :
a. { 001, 010, 011, 11,} merupakan kode awalan
b. {001, 010, 01, 111} bukan merupakan kode awalan karena 01
merupakan awalan dari 010
Penyelesaian contoh 2 :
a. { 001, 010, 011, 11,}
1
11
1
0
0
0
0
111001
001000

8. 3. Kode Huffman
• Dalam komunikasi data, pesan (message) yang dikirim
seringkali ukurannya sangat besar sehingga waktu pengirimannya
lama. Begitu juga dalam penyimpanan data, arsip (file) yang
berukuran besar memakan ruang penyimpanan yang besar. Kedua
masalah ini dapat diatasi dengan mengkodekan pesan atau isi
sesingkat mungkin, sehingga waktu pengiriman pesan juga relatif
cepat, dan ruang penyimpanan yang dibutuhkan juga sedikit. Cara
pengkodean seperti ini disebut pemampatan (compression) data.
Pemampatan data dilakukan dengan mengkodekan setiap karekter
di dalam pesan atau di dalam arsip dikodekan dengan kode yang
lebih pendek. Kode Hufman merupakan salah satu metode
pengkodean dalam hal kompresi data.
• Sistem kode yang banyak digunakan adalah kode ASCII
(American Standard Code for Information Interchange).Dengan
kode ASCII, setiap karekter dikodekan dalam 8 bit biner.

10. Cara pembentukan Kode Huffman adalah dengan membentuk
pohon biner, yang dinamakan pohon Huffman, sebagai berikut:
a. Pilih dua simbol dengan peluang (probability) paling kecil
sebagai child kemudian kedua simbol tersebut dikombinasikan
sebagai parent peluang penjumlahan dari kedua simbol tersebut.
b. Pilih dua simbol berikutnya, termasuk simbol baru, yang
mempunyai peluang terkecil sebagai child kemudian kedua simbol
tersebut dikombinasikan sebagai parent peluang penjumlahan dari
kedua simbol tersebut.
c. Prosedur yang sama dilakukan pada dua simbol berikutnya
yang mempunyai peluang terkecil sebagai child kemudian kedua
simbol tersebut dikombinasikan sebagai parent peluang
penjumlahan dari kedua simbol tersebut.

11. Contoh 1 :
Carilah rangkain bit untuk string ABACCDA dengan menggunakan
pengkodean ASCII dan pohon Huffman
Contoh 2 :
Carilah rangkain bit untuk kalimat APA KABAR? Dengan
menggunakan pohon Huffman

12. Penyelesaian contoh 1 :
Rangkain bit untuk string ABACCDA dengan menggunakan
pengkodean ASCII adalah
01000001010000010010000010100010010000011010000011010
0010001000001
Jadi, dengan sistem pengkodean ASCII, representasi 7 huruf
membutuhkan 7 x 8 = 56 bit (7 byte).
Rangkain bit untuk string ABACDDA dengan menggunakan pohon
Huffman adalah
diurutkan dari yang terkecil

13. BD
B D
CBD
C BD
ACBD
A CBD
a.)
b.)
c.)
ACBD
A
0
0
0
1
1
1
C
B
CBD
BD
D
d.) Jadi ,
rangkaian bit
untuk ’ABACCDA’:
0110010101110
hanya 13 bit!

14. Penyelesaian contoh 2 :
Dengan menggunakan kode ASCII maka diperoleh 10 x 8 bit = 80
bit
Dengan menggunakan pohon Huffman
B RA ?KP sp
1 1 14 1 1 1
B R A?KP sp
1 1 1 41 1 1
diurutkan dari yang terkecil

15. 1
A
*1
P
1
2
spP
B R *1 A?K
1 1 1 2 41
1
K
*2
B
1
2
R *1 *2 A?
1 1 2 2 4
1
R
*3
?
1
2 *1 *2 *3 A
2 2 2 4
a.)
b.)
c.)

16. d.)
e.)
f.)
2
*1
*4
*2
2
4
2
*3
*5
*4
4
6
4
A
*6
*5
6
10
*3*4 A
2 4 4
A *5
4 6
*6
10

17. A
0 1
*6
*5
*3
R ?
*4
*1
spP K B
*2
Jadi rangkain bit untuk APA KABAR? Adalah
01100011011110011110100101 , hanya 26 bit

18. 4. Pohon Pencarian
• Adalah pohon biner yang stiap key diatur dalam suatu urutan
tertentu
• Digunakan untuk melakukan operasi pencarian , penyisipan
dan penghapusan elemen
• Simpul pada pohon pencarian berupa field kunci (key) pada
data record atau data itu sendiri
Key ( kunci) adalah nilai yang membedakan setiap simpul dengan
simpul yang lainya
• Key harus unik karena itu tidak ada 2 buah simpul atau lebih
yang mempunyai kunci yang sama

19. • Jika R adalah akar dan semua key yang tersimpan pada setiap
simpul tidak ada yang sama maka :
a. Semua simpul pada subpohon kiri mempunyai key lebih kecil
dari key R
b. Semua simpul di subpohon kanan mempunyai key nilai
besar dari key R
R
T1 T2
Kunci(T1) < Kunci( R)
Kunci(T2) > Kunci( R)

20. Contoh 1 :
Gambarkan kedalam pohon biner pencarian untuk data masukan
dengan urutan sebagai berikut : 50, 32, 18, 40, 60, 52, 5, 25, 70
Contoh 2 :
Bangunlah pohon pencarian (search tree) dengan urutan
pembacaan data adalah pisang, anggur, apel, kelapa, mangga,
pepaya, jambu, rambutan, dan durian.

21. Penyelesaian contoh 1 :
50
32
4018
50
52 70
5 25
60

22. Penyelesaian contoh 2 :
pisang
anggur rambutan
apel
kelapa
jambu mangga
durian pepaya

23. 5. Tranversal Pohon Biner
• Operasi dasar yang sering dilakukan pada pohon biner ialah
mengunjungi ( transversal ) setiap simpul tepat satu kali.
Misalkan T adalah pohon biner, akarnya R, upapohon T1dan
upapohon kanan T2.
• Proses yang dilakukan terhadap simpul yang dikunjungi
misalnya mencetak informasi yang disimpan didalam sampul,
memanifulasi nilai, dan sebagainya.
• Ada tiga macam skema mengunjungi simpul-simpul di dalam
pohon biner T :
1. Preorder : R, T1, T2
- kunjungi R ( sekaligus memproses simpul R )
- kunjungi T1 secara preorder
- kunjungi T2 secara preorder

24. 2. Inorder : T1 , R, T2
- kunjungi T1 secara inorder
- kunjungi R ( sekaligus memproses simpul R )
- kunjungi T2 secara inorder
3. Postorder : T1, T2 , R
- kunjungi T1 secara postorder
- kunjungi T2 secara postorder
- kunjungi R ( sekaligus memproses simpul R )

25. Contoh 1 :
Tinjau pohon biner T dibawah ini :

26. Contoh 2 :
Tinjau pohon ekspresi dibawah ini :

27. Penyelesaian contoh 1 :
Lintasan :
Preorder : M E B A D L P N V T Z
Inorder : A B D E L M N P T V Z
Postorder : A D B L E N T Z V P M
Penyelesaian contoh 2 :
preorder : c * d + e
inorder : (c + d) * e
postorder : c + d * e