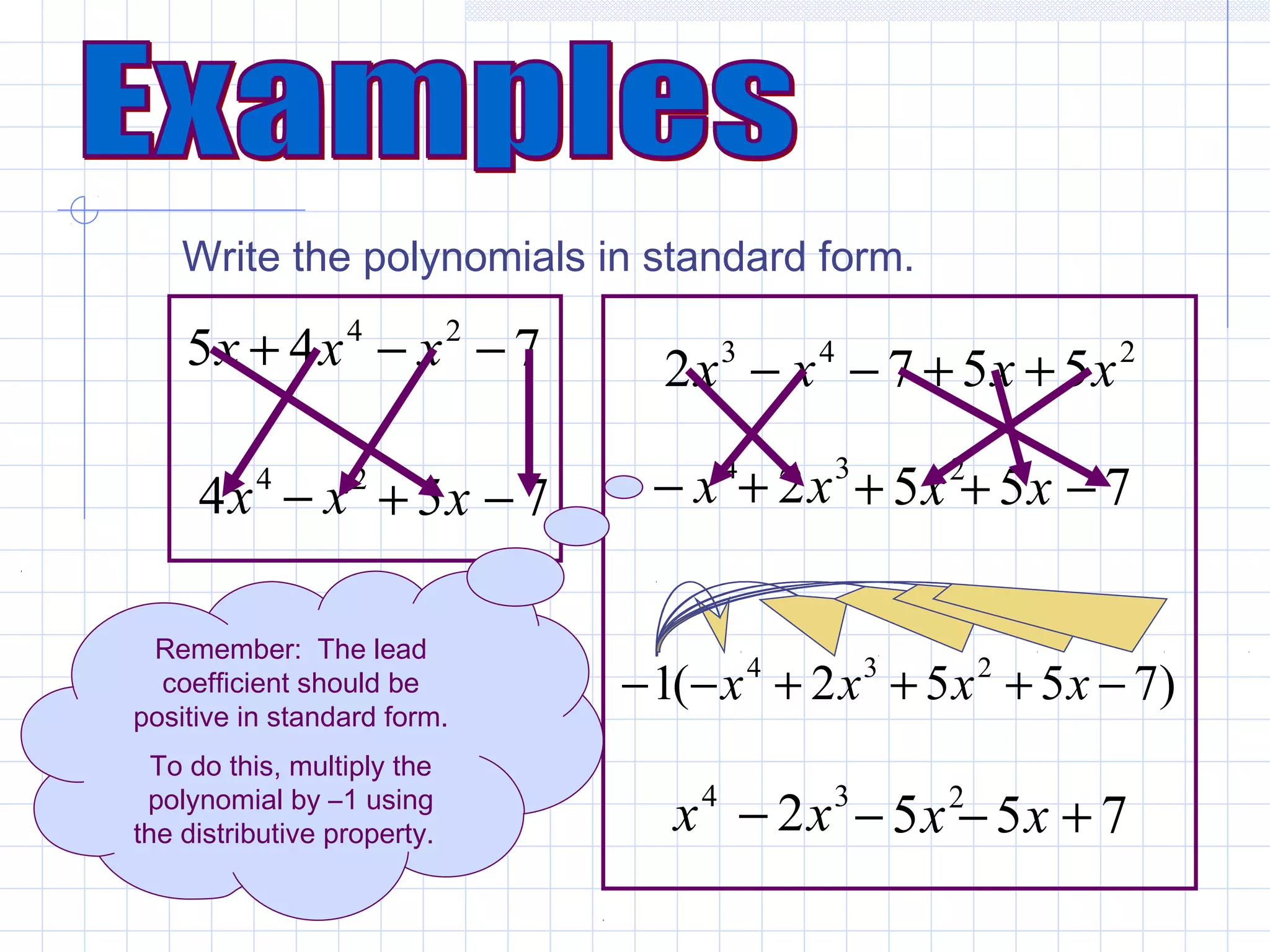
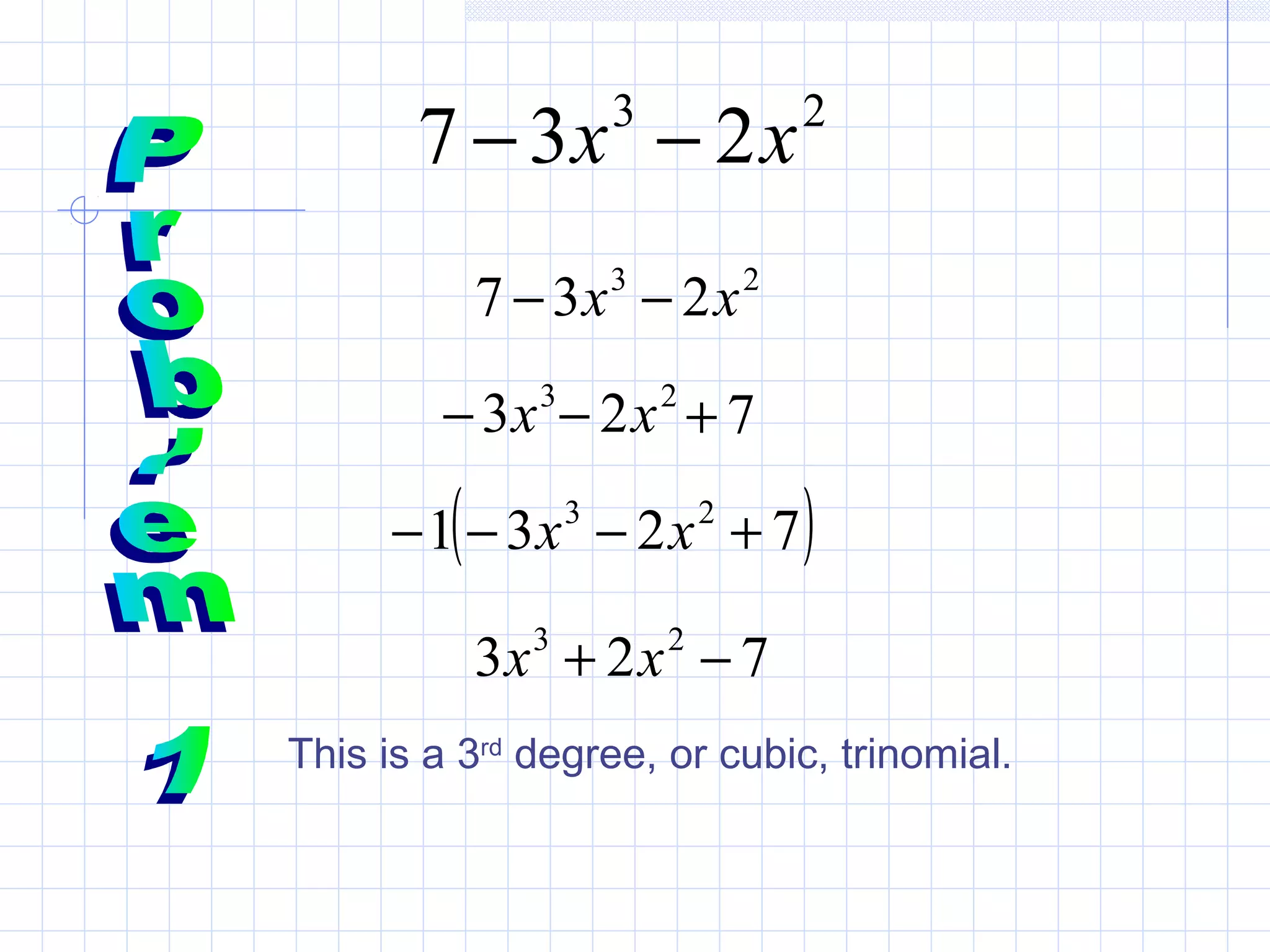This document provides information about polynomials presented by Lekhamol V R. It begins by stating the objectives of understanding polynomials, which are to determine the degree of a polynomial, classify polynomials, and write polynomials in standard form. It then defines key terms related to polynomials like monomial, polynomial, binomial, trinomial, coefficient, and degree. The document gives examples of finding the degree of monomials and polynomials. It demonstrates how to classify polynomials by degree and number of terms. Finally, it shows how to write polynomials in standard form and add or subtract polynomials by lining up like terms.

1. WELCOME

2. MATHAMATIC
S
Title:Polynomial
Presented By:Lekhamol V R
Roll No:22,1st
Year B.Ed Option: Mathematics

4. 1. Be able to determine the degree of a polynomial.
2. Be able to classify a polynomial.
3. Be able to write a polynomial in standard form.

5. Monomial: A number, a variable or the product of a
number and one or more variables.
Polynomial: A monomial or a sum of monomials.
Binomial: A polynomial with exactly two terms.
Trinomial: A polynomial with exactly three terms.
Coefficient: A numerical factor in a term of an algebraic
expression.

6. Degree of a monomial: The sum of the exponents of all of
the variables in the monomial.
Degree of a polynomial in one variable: The largest
exponent of that variable.
Standard form: When the terms of a polynomial are
arranged from the largest exponent to the smallest
exponent in decreasing order.

7. What is the degree of the monomial?
24
5 bx
The degree of a monomial is the sum of the
exponents of the variables in the monomial.
The exponents of each variable are 4 and 2. 4+2 = 6.
The degree of the monomial is 6.
The monomial can be referred to as a sixth degree
monomial.

8. A polynomial is a monomial or the sum of monomials
2
4x 83 3
−x 1425 2
−+ xx
Each monomial in a polynomial is a term of the
polynomial.
The number factor of a term is called the coefficient.
The coefficient of the first term in a polynomial is the
lead coefficient.
A polynomial with two terms is called a binomial.
A polynomial with three terms is called a trinomial.

9. 14 +x
83 3
−x
1425 2
−+ xx
The degree of a polynomial in one variable is the
largest exponent of that variable.
2 A constant has no variable. It is a 0 degree polynomial.
This is a 1st
degree polynomial. 1st
degree polynomials are linear.
This is a 2nd
degree polynomial. 2nd
degree
polynomials are quadratic.
This is a 3rd
degree polynomial. 3rd
degree polynomials are
cubic.

10. Classify the polynomials by degree and number of terms.
Polynomial
a.
b.
c.
d.
5
42 −x
xx +2
3
14 23
+− xx
Degree
Classify by
degree
Classify by
number of
terms
Zero Constant Monomial
First Linear Binomial
Second Quadratic Binomial
Third Cubic Trinomial

11. To rewrite a polynomial in standard form, rearrange
the terms of the polynomial starting with the largest
degree term and ending with the lowest degree term.
The leading coefficient, the coefficient of the first
term in a polynomial written in standard form, should be
positive.

12. 745 24
−−+ xxx
x5+4
4x 2
x− 7−
Write the polynomials in standard form.
243
5572 xxxx ++−−
3
2x+4
x− 7−x5+2
5x+
)7552(1 234
−+++−− xxxx
3
2x−4
x 7+x5−2
5x−
Remember: The lead
coefficient should be
positive in standard form.
To do this, multiply the
polynomial by –1 using
the distributive property.

13. Write the polynomials in standard form and identify the
polynomial by degree and number of terms.
23
237 xx −−1.
2. xx 231 2
++

14. 23
237 xx −−
23
237 xx −−
3
3x− 2
2x− 7+
( )7231 23
+−−− xx
723 23
−+ xx
This is a 3rd
degree, or cubic, trinomial.

15. xx 231 2
++
xx 231 2
++
2
3x x2+ 1+
This is a 2nd
degree, or quadratic, trinomial.

16. Add: (x2
+ 3x + 1) + (4x2
+5)
Step 1: Underline like terms:
Step 2: Add the coefficients of like terms, do
not change the powers of the variables:
Adding Polynomials
(x2
+ 3x + 1) + (4x2
+5)
Notice: ‘3x’ doesn’t have a like term.
(x2
+ 4x2
) + 3x + (1 + 5)
5x2
+ 3x + 6

17. Some people prefer to add polynomials by stacking
them. If you choose to do this, be sure to line up the
like terms!
Adding Polynomials
(x2
+ 3x + 1) + (4x2
+5)
5x2
+ 3x + 6
(x2
+ 3x + 1)
+ (4x2
+5)
Stack and add these polynomials: (2a2
+3ab+4b2
) +
(7a2+ab+-2b2
)
(2a2
+3ab+4b2
) + (7a2+ab+-
2b2
)
(2a2
+ 3ab + 4b2
)
+ (7a2
+ ab + -2b2
)
9a2
+ 4ab + 2b2

18. Adding Polynomials
1) 3x3
− 7x( )+ 3x3
+ 4x( )= 6x3
− 3x
2) 2w
2
+ w − 5( )+ 4w
2
+ 7w +1( )= 6w2
+ 8w − 4
3) 2a3
+ 3a2
+ 5a( )+ a3
+ 4a + 3( )=
3a3
+ 3a2
+ 9a + 3
• Add the following polynomials; you may stack them if
you prefer:

19. Subtract: (3x2
+ 2x + 7) - (x2
+ x + 4)
Subtracting Polynomials
Step 1: Change subtraction to addition (Keep-
Change-Change.).
Step 2: Underline OR line up the like terms
and add.
(3x2
+ 2x + 7) + (- x2
+ - x + - 4)
(3x2
+ 2x + 7)
+ (- x2
+ - x + - 4)
2x2
+ x + 3

20. Subtracting Polynomials
1) x2
− x − 4( )− 3x2
− 4x +1( )= −2x
2
+ 3x − 5
2) 9y
2
− 3y + 1( )− 2y
2
+ y − 9( )= 7y2
− 4y +10
3) 2g
2
+ g − 9( )− g
3
+3g
2
+ 3( )= −g3
− g2
+ g −12
• Subtract the following polynomials by changing to
addition (Keep-Change-Change.), then add:

21. THANK
YOU