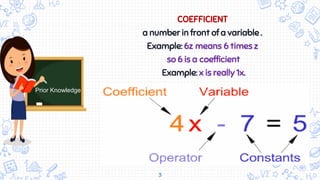
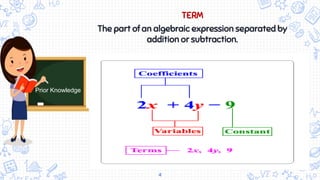
This document defines key concepts related to polynomials, including: - Variables and constants, with variables represented by letters like x and y. - Algebraic expressions that combine constants and variables. - The coefficient as the number in front of a variable. - A term as a part of an algebraic expression separated by addition or subtraction. - The degree as the highest power of the variable in a polynomial. - A polynomial defined as an algebraic expression with positive whole number exponents, that can be classified based on its degree or number of terms.

1. CONSTANT
A value that does not change.
VARIABLE
A letter that represents an unknown number.
Eg: commonly used letters to represent variables are 𝑥, 𝑦, 𝑧, and 𝑡
Prior Knowledge
1
Subtopic- 1
Introduction to polynomials
Learning objectives:
• To recall concepts of variables , constants
and algebraic expressions
• To define polynomial
• To understand the concept of degree
• To classify polynomials on the basis of
degree and number of terms.

2. ALGEBRAIC EXPRESSIONS
Combination of constants and variables.
Eg: x+2 , 2y+7 etc.
Prior Knowledge
2

3. COEFFICIENT
a number in front of a variable .
Example: 6z means 6 times z
so 6 is a coefficient
Example: x is really 1x.
Prior Knowledge
3

4. TERM
The part of an algebraic expression separated by
addition or subtraction.
Prior Knowledge
4

5. Degree
DEGREE: the highest power of the variable.
Eg: (i). 5x5+4x2+3
The degree is 5.
(ii)12x3 -5x2 + 2
The degree is 3.
(iii) 4x +12
The degree is 1.
5

6. INTRODUCTION
Polynomial comes from the words poly(meaning “many”) and
nomial(meaning “term”)……….so it says “many terms”.
6

7. So, let’s define Polynomial Mathematically
A polynomial is an algebraic expression which is a
combination of the constants, variables and positive
exponents(whole number)
Definition
7

8. Now, we can classify polynomial on the basis of terms and degrees
FIRSTLY,CLASSIFICATION OF POLYNOMIALS ON THE BASIS OF TERMS:-
POLYNOMIALS
MONOMIAL eg:3x
(one term)
BINOMIAL eg:
x – y(two terms)
TRINOMIAL. eg:
3x2 − 3y2 + 2.(three
terms)
On theBasis of
terms
8

9. On the Basis of
degrees
CLASSIFICATION OF POLYNOMIALS ON THE BASIS OF DEGREE:-
9

10. Examples
POLYNOMIALS DEGREE CLASSIFY BY
DEGREE
CLASSIFY BY
NO.OF TERMS
5 0 Constant Monomial
2x- 4 1 Linear Binomial
3𝑥3+4x+1 3 Cubic Trinomial
10

11. +.STANDARD FORM
+The Standard Form writing a polynomial is to put the
terms with the highest degree first.
Example: Put this in Standard Form 3𝑥2
- 7 +4𝑥3
+ 𝑥6
The highest degree is 6, so that goes first, then 3, 2 and
then the constant last:
𝑥6
+ 4𝑥3
+ 3𝑥2
− 7
Standard Form
11

12. Standard Form
Examples: WRITE THE FOLLOWING POLYNOMIALS IN
STANDARD FORM:
1) 8y3-4y+y2-3. 2) 3x2-4x3-2x
3) 6-4y 4) 4a+6a2+5a3
5) n3-5n5+8
Answers: 1)8y3+y2-4y-3 2)-4x3+3x2-2x
3)-4y+6 4)5a3 +6a2+4a
5) -5n5+n3+8
12