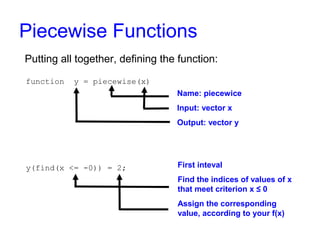
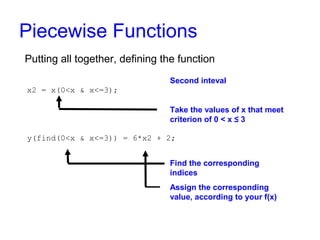
This document discusses how to define and plot piecewise functions in Matlab without using loops. It explains that a piecewise function is made up of multiple subfunctions, each applying to an interval of the main function's domain. It provides an example of a 4-interval piecewise function and shows how to define it in Matlab using specially selected indices and the "find" function to assign values based on the interval. Defining the piecewise function this way allows it to be plotted vectorized, without scalar values or iterations.

1. Piecewise Functions
In Matlab

2. Piecewise Functions
• A piecewise function is a function which is
defined by multiple sub functions, each
sub function applying to a certain interval
of the main function's domain.

3. Piecewise Functions
• We’ll show one way to define and plot
them in Matlab without using loops.
• We’ll use a vectorized way: no scalar
values or iterations will be used.

4. Piecewise Functions
Let’s assume a function with 4 intervals
ì
ï ï í
2 0
6 2 0 3
( ) 2
ï ï
î
£
if x
x if x
+ < £
x x if x
- + + < £
6 11 3 8
- <
=
if x
f x
5 8

5. Piecewise Functions
This is the plot of that 4-interval function
x
y = f(x)

6. Piecewise Functions
Ideally, we should type something like this
and get the plot shown above
x = -2 : .01 : 9;
y = piecewise(x);
plot(x, y)
interval of interest
function to be defined
call the plot, just as it’s done
with any other function

7. Piecewise Functions
The interesting part is how to define the
piecewise function without going number-by-number
in the domain, but going instead
interval-by-interval.
To accomplish this, we’ll use two ideas:
• Specially selected indices.
• Function find.

8. Piecewise Functions
First important concept: special indices
In Matlab, if we have vector x = [-2 -1 0 1 2 3 4 5 6 7 8 9], and do this:
i2 = x(0 < x & x <= 3)
we’ll take all the values in vector x that meet the condition 0 < x ≤ 3, that is,
i2 = [1 2 3]
If we do:
i3 = x(3 < x & x <= 8)
we’ll take all the values in vector x that meet the condition 3 < x ≤ 8, thus
i3 = [4 5 6 7 8]

9. Piecewise Functions
Second important concept: function find
In Matlab, if we have vector x = [-2 -1 0 1 2 3 4 5 6 7 8 9], and do this:
find(0 < x & x <= 3)
we’ll find the indices (not values) in vector x that meet 0 < x ≤ 3, so we’ll get
the vector [4 5 6].
If we do:
find(3 < x & x <= 8)
we’ll get the vector [7 8 9 10 11]

10. Piecewise Functions
Putting all together, defining the function:
function y = piecewise(x)
y(find(x <= -0)) = 2;
Name: piecewice
Input: vector x
Output: vector y
First interval
Find the indices of values of x
that meet criterion x ≤ 0
Assign the corresponding value,
according to your f(x)

11. Piecewise Functions
Putting all together, defining the function
Second inteval
Take the values of x that meet
criterion of 0 < x ≤ 3
Find the corresponding indices
Assign the corresponding value,
according to your f(x)
x2 = x(0<x & x<=3);
y(find(0<x & x<=3)) = 6*x2 + 2;

12. Piecewise Functions
Putting all together, defining the function
Third interval
Take the values of x that meet
criterion of 3 < x ≤ 8
Find the corresponding indices
Assign the corresponding value,
according to your f(x)
x3 = x(3<x & x<=8);
y(find(3<x & x<=8)) = -x3.^2 +
6*x3 + 11;

13. Piecewise Functions
Putting all together, defining the function
Fourth inteval
Take the corresponding indices
for 8 < x
We don’t need the values of x
now, because they’re not
needed for the assignation in
this interval
y(find(8 < x)) = -5;

14. Piecewise Functions
Putting all together. This is the final code…
function y = piecewise(x)
y(find(x <= -0)) = 2;
x2 = x(0 < x & x <= 3);
y(find(0 < x & x <= 3)) = 6*x2 + 2;
x3 = x(3 < x & x <= 8);
y(find(3 < x & x <= 8)) = -x3.^2 + 6*x3 + 11;
y(find(8 < x)) = -5;

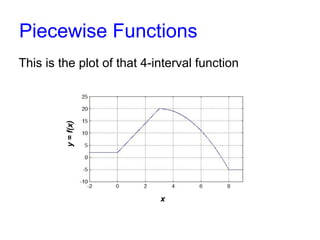
15. Piecewise Functions
Now, if we type this code…
clc, clear all, close all
x = -2 : .01 : 9;
y = piecewise(x);
plot(x, y)
axis([-2 9 -10 25])
grid on
We get this plot…

16. Piecewise Functions
For more examples and details, visit:
matrixlab-examples.com/piecewise-function.html