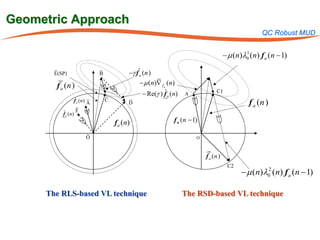
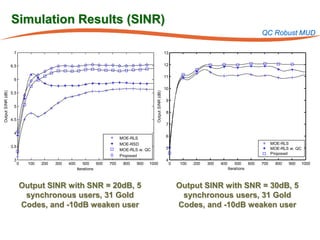
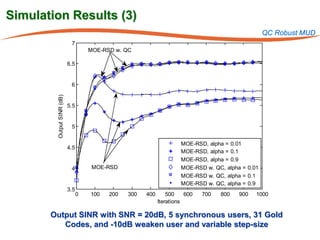
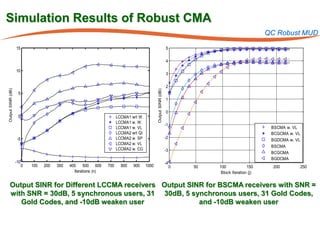
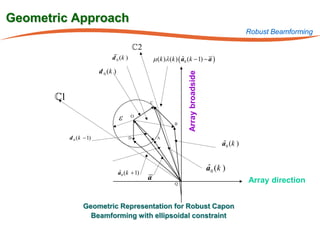
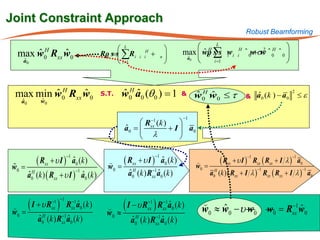
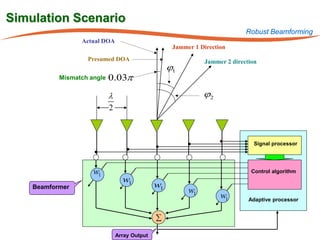
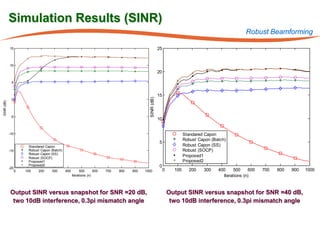
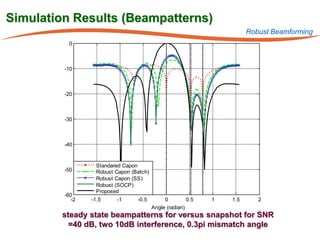
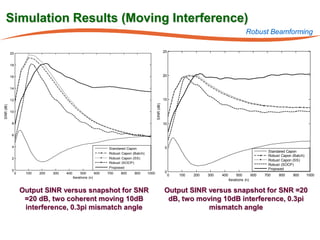
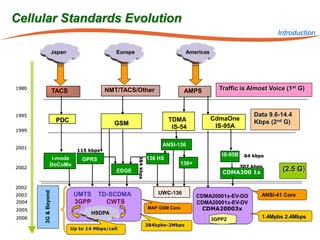
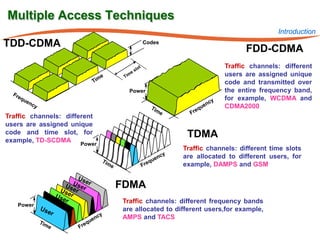
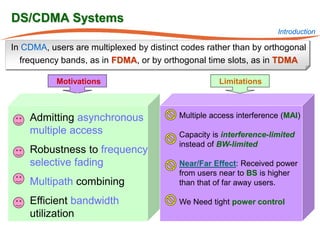
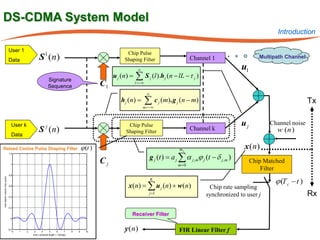
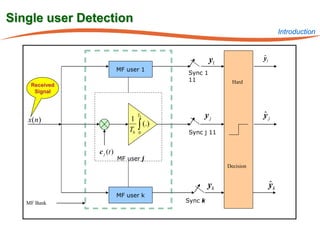
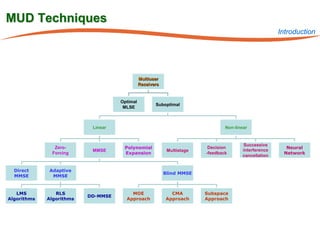
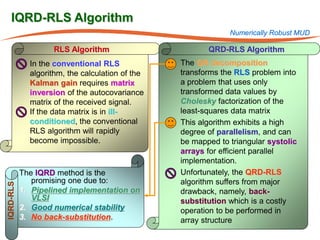
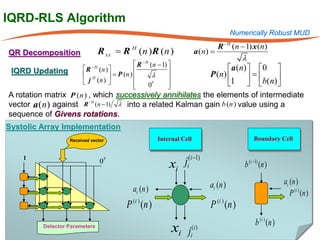
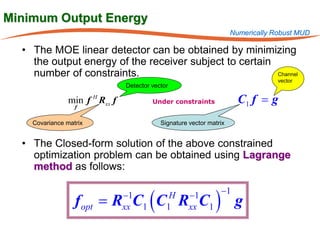
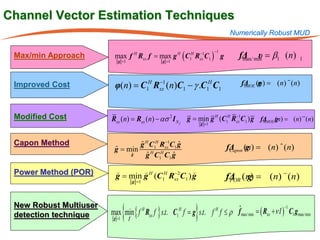
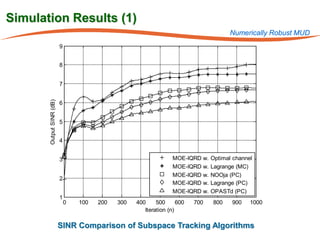
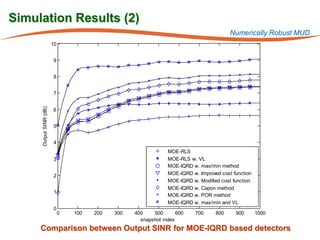
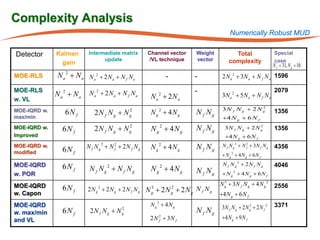
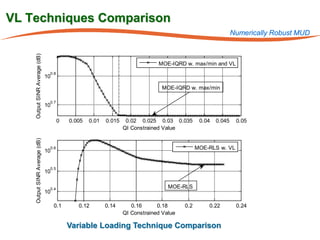
The document summarizes research on robust multiuser detection techniques for direct-sequence code-division multiple access (DS-CDMA) systems. It introduces numerically robust algorithms like the inverse QR decomposition RLS algorithm to overcome issues with conventional RLS algorithms in ill-conditioned environments. It also discusses the minimum output energy detector and its implementation using the IQRD-RLS algorithm. Finally, it outlines various channel estimation techniques used for multiuser detection like the max/min, improved cost, modified cost, Capon, and power methods.

1. Ayman Elnashar
ECMS (MobiNil)
Supervisors:
Prof. Dr. Hamdy El-Mikati Prof. Dr. Said El-Noubi
Mansoura University Alexandria University
30 April 2005

2. Agenda
Introduction
Numerically Robust Multiuser Receivers
Quadratically Constrained Robust MUD
Robust Adaptive Beamforming
Thesis Contributions & Publications

3. Cellular Standards Evolution
Introduction
Japan Europe Americas
1980 Traffic is Almost Voice (1st G)
TACS NMT/TACS/Other AMPS
1995 Data 9.6-14.4
PDC TDMA CdmaOne
GSM Kbps (2nd G)
IS-54 IS-95A
1999
ANSI-136
2001
115 kbps
IS-95B 64 kbps
i-mode 136 HS
384 kbps
GPRS
DoCoMo 136+
2002 307 kbps
EDGE CDMA200 1x
(2.5 G)
2002
3G & Beyond
2003 UMTS TD-SCDMA UWC-136 ANSI-41 Core
CDMA20001x-EV-DO
2004 3GPP CWTS CDMA20001x-EV-DV
2005 MAP GSM Core CDMA20003x
HSDPA
2006 3GPP2 1.4Mpbs 2.4Mbps
384kpbs-2Mbps
Up to 14 Mbps/cell

4. Multiple Access Techniques
Introduction
TDD-CDMA Codes
FDD-CDMA
Traffic channels: different
users are assigned unique
code and transmitted over
Power the entire frequency band,
for example, WCDMA and
CDMA2000
Traffic channels: different
users are assigned unique
code and time slot, for TDMA
example, TD-SCDMA Power
Traffic channels: different time slots
are allocated to different users, for
example, DAMPS and GSM
FDMA
Traffic channels: different frequency bands
Power
are allocated to different users,for example,
AMPS and TACS

5. DS/CDMA Systems
Introduction
In CDMA, users are multiplexed by distinct codes rather than by orthogonal
frequency bands, as in FDMA, or by orthogonal time slots, as in TDMA
Motivations Limitations
Admitting asynchronous Multiple access interference (MAI)
multiple access Capacity is interference-limited
instead of BW-limited
Robustness to frequency
selective fading Near/Far Effect: Received power
from users near to BS is higher
Multipath combining than that of far away users.
Efficient bandwidth We Need tight power control
utilization

6. DS-CDMA System Model
Introduction
User 1
Chip Pulse
Data S 1 ( n) Shaping Filter Channel 1 Multipath Channel
∞ u1
Signature
=
u j ( n) ∑S j (l ).h j (n − lL − τ j )
Sequence C1 l = −∞
∞
=h j ( n) ∑ c (m) .g (n − m)
m = −∞
j j Tx
User k j Chip Pulse uj Channel noise
S ( n) Shaping Filter
Channel k w (n )
Data
Raised Cosine Pulse Shaping Filter ϕ (t ) mj x ( n)
= a j ∑ α j ,mϕ j (t − δ j ,m )
1.2
g j (t )
1
Cj m=0
Chip Matched
Filter
0.8
ϕ (T c − t )
root-raised cosine chip pulse
K
0.6 =
x ( n) ∑ u ( n) + w ( n)
j Chip rate sampling
0.4
j =1 synchronized to user j Rx
0.2
Receiver Filter
0
-0.2
0 1 2 3 4 5 6 7 8 9 10
y ( n) FIR Linear Filter f
time t (channel length = 10chips)

7. Single user Detection
Introduction
y1 ˆ
y1
MF user 1
Sync 1
11 Hard
Received
Signal
1 b
T yj ˆ
yj
x ( n)
∫ (.)
Tb 0 Sync j 11
c j (t )
MF user j
Decision
yk ˆ
yk
MF user k
MF Bank Sync k

8. Multiuser Detection
Introduction
 Multiuser detection considers signals from all users
which lead us to joint detection
 Reduces multiple access interference and hence
leads to capacity increase
 Alleviates the near/far problem
 Power Control can be used but not necessary
 MUD can be implemented in the base station (BS) or
mobile station (MS), or both
 Transmission for the Downlink MS is synchronous and
equal-power
 MUD algorithm is simpler for synchronous CDMA
 In case of Uplink the Transmission is Asynchronous
which is more complex and need robust algorithms

9. MUD Techniques
Introduction
Multiuser
Receivers
Optimal
Suboptimal
MLSE
Linear Non-linear
Successive
Zero- Polynomial Decision Neural
MMSE Multistage interference
Forcing Expansion -feedback Network
cancellation
Direct Adaptive
Blind MMSE
MMSE MMSE
LMS RLS MOE CMA Subspace
DD-MMSE
Algorithms Algorithms Approach Approach Approach

10. Linear Multiuser Receivers
Introduction
Linear receivers are of great significance due to ease of
practical implementation
The linear detector output is a linear combination of the
received chip sampled signals:
y ( n) = f H
( n) x ( n)
In BPSK the bit decision is made according to:
s1 (n) = sgn ( Re { y1 (n)} )
ˆ
The detector output energy is given by:
{
= E f H x ( n)
E y ( n) } {
= f H Rxx f
2 2
}
The received signal autocorrelation matrix is given by:
Rxx (n) = E { x (n) x H (n)}

11. Agenda
Introduction
Numerically Robust Multiuser Detection
Quadratically Constraint Robust MUD
Robust Adaptive Beamforming
Thesis Contributions & Publications

12. IQRD-RLS Algorithm
Numerically Robust MUD
RLS Algorithm QRD-RLS Algorithm
In the conventional RLS • The QR decomposition
algorithm, the calculation of the transforms the RLS problem into
Kalman gain requires matrix a problem that uses only
inversion of the autocovariance transformed data values by
matrix of the received signal. Cholesky factorization of the
If the data matrix is in ill- least-squares data matrix
conditioned, the conventional • This algorithm exhibits a high
RLS algorithm will rapidly degree of parallelism, and can
become impossible. be mapped to triangular systolic
arrays for efficient parallel
implementation.
The IQRD method is the • Unfortunately, the QRD-RLS
promising one due to: algorithm suffers from major
IQRD-RLS
1. Pipelined implementation on drawback, namely, back-
VLSI substitution which is a costly
2. Good numerical stability operation to be performed in
3. No back-substitution. array structure

13. IQRD-RLS Algorithm
Numerically Robust MUD
R − H (n − 1) x (n)
QR Decomposition R xx = R (n )R (n )
H
a ( n) =
λ
 R − H (n − 1) 
IQRD Updating  R (n ) 
−H
   a ( n)   0 
 H  = P (n )  λ  P ( n)   = b( n) 
 j (n )  
 0 T

 1   
A rotation matrix P (n ) , which successively annihilates the elements of intermediate
vector a ( n) against R − H (n − 1) λ into a related Kalman gain b (n ) value using a
sequence of Givens rotations.
Systolic Array Implementation
Received vector Internal Cell Boundary Cell
1
0T
xi ji(i −1) b (i −1) (n )
ai (n ) ai (n )
ai (n ) P (i ) (n )
P (i ) (n ) P (i ) (n )
b (i ) (n )
Detector Parameters
xi ji(i )

14. Minimum Output Energy
Numerically Robust MUD
• The MOE linear detector can be obtained by minimizing
the output energy of the receiver subject to certain
number of constraints. Channel
vector
Detector vector
min f H Rxx f
f
Under constraints C1 f = g
Covariance matrix Signature vector matrix
• The Closed-form solution of the above constrained
optimization problem can be obtained using Lagrange
method as follows:
f opt = R C1 ( C R C1 ) g
−1 H −1 −1
xx 1 xx

15. MOE Implementation Using IQRD-RLS
Numerically Robust MUD
{ }
−1 −1
Detector Estimation f = R H (n )R (n )  −1 C 1 C 1H R H (n )R (n )  −1 C 1 g Δ( n ) =  R H ( n ) R ( n )  C 1
 
   
Π (n ) = C 1H Δ(n ) fΔn) = (n) g −1 (n)
( Π Δ= λ −1Δ(n − 1) − j (n )π H (n )
(n ) π (n ) = C 1H j (n )
λ 2 Π −1 (n − 1)π (n )π H (n )Π −1 (n − 1)
Π (n ) λ Π (n − 1) − π (n )π (n )
= −1 H
Π = λ Π (n − 1) +
−1
(n ) −1
1 − λπ H (n )Π −1 (n − 1)π (n )
Channel Estimation max f max/ min R H (n) R(n) f max/ min
g =1
H
fΔ min = β1 (n)
max/ υ 1
−1 λ Π −1 (n − 1)π (n )
υ1 gmax/ min max g Π (n) g
= H
Ψ (= λΨ (n − 1) + d (n )d H (n ) d (n ) = 1 − λπ H (n )Π −1 (n − 1)π (n )
n)
g =1
Subspace Tracking
Any orthogonal subspace tracking algorithm can be employed for
tracking the principle component of the.
• orthogonal projection approximation subspace tracking (OPASTd)
• normalized orthogonal OJA (NOOJA).

16. Subspace Tracking (new)
Numerically Robust MUD
(C R C1 ) g
H H −1 −1
Cost Function max g 1 xx
g =1
1
Ψ n ( g , ζ ) g H (n − 1)Π (n ) g (n − 1) + ζ (n − 1)(1 − g H (n − 1) g (n − 1))
=
2
Channel Update Gradient Vector
g (Ψ) g g (n − 1) − µ∇ g ( , ζ )
n= ∑ g (n) Π (n) g (n − 1) − ζ (n) g (n − 1)
=
Step-Size Estimation
Ψ = Ψ n −1 ( g, ζ ) + 2µ (n − 1) g H (n − 1) Π (n) ∑ H (n) − µ 2 (n − 1) ∑ H (n) Π (n) ∑ g (n)
n ( g, ζ ) g g
Optimum Step-Size α gΠ(n − 1) (n) ∑ g (n)
H
µopt (n) = H
∑ g ( n) Π ( n) ∑ g ( n) + η
Lagrange Multiplier
aζ 2 (n ) − 2b ζ (n ) + c = µopt (n − 1)
a
1+ µ
b =opt (n − 1) gΠ (n −g (n ) (n − 1)
H
1)
−b ± b 2 − ac
ζ (n ) = = µopt (n − 1) gΠ (n − 1)
c H
g 2
(n ) (n − 1) + 2 Π (n −g (n ) (n − 1)
g H
1)
a

17. Channel Vector Estimation Techniques
Numerically Robust MUD
max f H Rxx f = max g H ( C1H Rxx1C1 ) g fΔ min = β1 (n)
max/ υ
− −1
Max/min Approach 1
= 1= 1
g g
Improved Cost = C1H Rxx1 (n)C1 − γ .C1H C1
φ(n) − fΔ (g ) = (n)  (n)
IMOE n
Modified Cost Rxx (n) Rxx (n) − ασ 2 I N f g = min g H (C1H Rxx1C1 ) g fΔ gn) = (n) (n)
= −
MMOE (
g =1
Capon Method −
g H C1H Rxx1C1 g
ˆ ˆ fΔ (g ) = (n) ˆ (n)
g = min
ˆ Capon n
ˆ
g g H C1H C1 g
ˆ ˆ
Power Method (POR)    
−
g = min g H (C1H Rxx2C1 ) g
g =1 POR g
fΔ (n) = (n) (n)
New Robust Multiuser
detection technique g =1
{ f }
max min { f H Rxx f = g s.t. f H f ≤ ρ fˆmax/= ( Rxx +ν I ) C1 gmax/ min
} s.t. C1H f min
−1

18. Simulation Results (1)
Numerically Robust MUD
9
8
7
Output SINR (dB)
6
5
4
3 MOE-IQRD w. Optimal channel
MOE-IQRD w. Lagrange (MC)
MOE-IQRD w. NOOja (PC)
2
MOE-IQRD w. Lagrange (PC)
MOE-IQRD w. OPASTd (PC)
1
0 100 200 300 400 500 600 700 800 900 1000
Iteration (n)
SINR Comparison of Subspace Tracking Algorithms

19. Simulation Results (2)
Numerically Robust MUD
10
9
8
7
Output SINR (dB)
6
5
4
MOE-RLS
3 MOE-RLS w. VL
MOE-IQRD w. max/min method
2 MOE-IQRD w. Improved cost function
MOE-IQRD w. Modified cost function
MOE-IQRD w. Capon method
1
MOE-IQRD w. POR method
MOE-IQRD w. max/min and VL
0
0 100 200 300 400 500 600 700 800 900 1000
snapshot index
Comparison between Output SINR for MOE-IQRD based detectors

20. Complexity Analysis
Numerically Robust MUD
Detector Kalman Intermediate matrix Channel vector Weight Total Special
update /VL technique vector complexity case
gain = 31, N g 10
Nf =
MOE-RLS Na 2 + Na Na2 + 2Na + N f Na - - 2 N a 2 + 3 N a + N f N a 1596
MOE-RLS Na2 + 2Na + N f Na - 2079
Na2 + Na Na + 2Na
2 3N a 2 + 5 N a + N f N a
w. VL
3N f N g + 2 N g
2
MOE-IQRD w. 6N f 2N f Ng + N 2
g
Ng + 4Ng
2
N f Ng 1356
max/min +4 N g + 6 N f
2N f Ng + Ng
2
Ng 2 + 4Ng 3N f N g + 2 N g
2
MOE-IQRD w. 6N f N f Ng 1356
Improved +4 N g + 6 N f
MOE-IQRD w.
6N f N f Ng 2 + N 2 + 2N f Ng
f Ng 2 + 4Ng N f Ng N f N g 2 + N 2 + 3N f N g
f 4356
modified
+ Ng + 4Ng + 6N f
2
MOE-IQRD N f Ng 2 + 2N f Ng 4046
6N f N f Ng + N f Ng
2
Ng + 4Ng
2
N f Ng
w. POR + Ng 2 + 4Ng + 6N f
MOE-IQRD N g + 3N f N g + 4 N g 2
3
2556
6N f 2Ng + 2Ng + 2N f Ng
2
N + 2N + 2Ng N f Ng
3 2
w. Capon g g +4 N g + 6 N f
MOE-IQRD Ng 2 + 4Ng 3N f N g + 2 N g2 + 2 N f 2 3371
w. max/min 6N f 2N f Ng + Ng
2
N f Ng
and VL 2 N 2 + 3N f
f
+4 N g + 9 N f

21. VL Techniques Comparison
Numerically Robust MUD
Output SINR Average (dB)
MOE-IQRD w. max/min and VL
0.8
10
MOE-IQRD w. max/min
0.7
10
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0.04 0.045 0.05
QI Constrained Value
Output SINR Average (dB)
0.6 MOE-RLS w. VL
10
0.5
10
0.4 MOE-RLS
10
0.1 0.12 0.14 0.16 0.18 0.2 0.22 0.24
QI Constrained Value
Variable Loading Technique Comparison

22. Agenda
Introduction
Numerically Robust Multiuser Receivers
Quadratically Constrained Robust MUD
Robust Adaptive Beamforming
Thesis Contributions & Publications

23. MOE Implemented using PLIC structure
QC Robust MUD
Non-Adaptive Part
y ( n)
yc (n) +
f qH
Received vector
-
ya ( n )
x ( n)
BH f aH
Adaptive
Algorithm
Blocking Matrix
Reduced Rank Filter
Optimal Detector
min ( f c − Bf a ) R xx ( f c − Bf a )
H
f= f c − Bf a
H
min f Rxx f
f fa
( ) ( )
−1 −1
f a ( opt ) = B Rxx B
H H
B Rxx f c fc = C 1 C C 1 1
H
g

24. Robust MOE with QI constraint
QC Robust MUD
f a = f c − Bf a ) Rxx ( f c − Bf a )
min (
H
fa
Under constraints f aH f a ≤ β 2
( R B + λ0I )
−1
Optimal Detector f a (=
opt ) pB
p B = PB f c R B = B H R xx B PB = B H Rxx
( I + λ0R (n ) ) R (n ( I + λ0R (n ) ) f a (n )
−1 −1 −1 −1 −1
RLS-based VL f a (n ) = ) p B (n ) =B B B
−
f a (n ) = R B 1 (n ) p B (n )
Taylor Series f a (n ) ≈ f a (n ) − γ fˆa (n ) f aH f a ≤ β 2
−
fˆa (n ) = R B 1 (n )f a (n )
γ=

−b ± Re {  
b 2 − 4ac }
2a

a = fˆ H
a ( n )fˆ (n )
a
Lagrange Multiplier
 {
b = −2 Re f aH ( n) f a ( n)
ˆ }
= f a H ( n )f a (n ) − β 2

c

25. Robust MOE with QI constraint (RSD-VL)
QC Robust MUD
Ψ fa = f c − Bf a ) Rxx ( f c − Bf a ) + λ0 s ( f aH f a − β 2 )
1
(
H
Cost Function
2
Detector Update f a (n ) f a (n − 1) − µ∇f a (n )
=
Gradient Vector ∇f a (n ) = B H R xx (n )f c + B H R xx (n )Bf a (n − 1) + λ0f a (n − 1)
−
Robust Detector f a (n= f a (n − 1) − µ (R B (n )f a (n − 1) − p B (n )) − µλ0f a (n − 1)
)
Non-Robust f a (n= f a (n − 1) − µ [ R B (n )f a (n − 1) − p B (n )]
 )
(  ) (  )
H
QI Constraint f a (n ) − µλ0f a (n − 1) f a (n ) − µλ0f a (n − 1) ≤ β 2
Quadratic
Equation
2 H 2
0 { a 0 fa }
 H (n) f (n − 1) λ +  H (n)  (n) − β 2 =
µ f a (n − 1) f a (n − 1)λ − 2µ Re f a fa 0
= µ 2 f a (n − 1)
2
a
−b ± b 2 − 4ac
Lagrange Multiplier λ0 =
2a
b =(n − 1)
f
H
{
−2µ Re  a (n) f a }
 (n ) 2 − β 2
= fa
c

26. Optimum Step-size of MOE-RSD w. VL
QC Robust MUD
Ψ fa = f c − Bf a ) Rxx ( f c − Bf a ) + λ0 s ( f aH f a − β 2 )
1
(
H
Cost Function
2
Non-Robust Detector f a (n= f a (n − 1) − µ [ R B (n )f a (n − 1) − p B (n )]
 )
(  )  ( )
H
Updated Cost Function Ψ fa (n)
= f (n − 1) + µ B∇ fa (n) Rxx (n) f (n − 1) + µ B∇ fa (n)
Quadratic Equation 

Ψ fa (= Ψ fa (n − 1) + 2µ (n)∇ Ha (n) PB f (n − 1) + µ 2 (n)∇ Ha (n) RB (n)∇ fa (n)
n) 
f f
∂Ψ fa (n)
Differentiate =2∇ H (n) PB f (n − 1) + 2µ (n)∇ H (n) RB (n)∇ f (n)
f f zero
∂µ (n) a a a
2
α ∇ fa (n)
µopt (n) =
∇ H (n) RB (n)∇ f (n) + σ

fa a
Optimum Step-Size

27. Geometric Approach
QC Robust MUD
− µ (n)λ0 (n) f a (n − 1)
1
E(SP) B −γ fˆa (n )
f a (n ) − µ (n)∇ fa (n)
− Re(γ ) f (n)
ˆ
a
A C1
ˆ
f a ( n) A C
D f a (n )
ˆ F
f a ( n)
f a ( n) f a (n − 1)
O O
f a (n )
C2
− µ (n)λ02 (n) f a (n − 1)
The RLS-based VL technique The RSD-based VL technique

28. Simulation Results (SINR)
QC Robust MUD
7 13
6.5 12
11
6
10
Output SINR (dB)
Output SINR (dB)
5.5
9
5
8
4.5
7
4
MOE-RLS 6
MOE-RSD MOE-RLS
3.5 5 MOE-RLS w. QC
MOE-RLS w. QC
Proposed
Proposed
3 4
0 100 200 300 400 500 600 700 800 900 1000 0 100 200 300 400 500 600 700 800 900 1000
Iterations Iterations
Output SINR with SNR = 20dB, 5 Output SINR with SNR = 30dB, 5
synchronous users, 31 Gold synchronous users, 31 Gold
Codes, and -10dB weaken user Codes, and -10dB weaken user

29. Simulation Results (3)
QC Robust MUD
7
MOE-RSD w. QC
6.5
6
Output SINR (dB)
5.5
5
MOE-RSD, alpha = 0.01
4.5
MOE-RSD, alpha = 0.1
MOE-RSD, alpha = 0.9
4 MOE-RSD MOE-RSD w. QC, alpha = 0.01
MOE-RSD w. QC, alpha = 0.1
MOE-RSD w. QC, alpha = 0.9
3.5
0 100 200 300 400 500 600 700 800 900 1000
Iterations
Output SINR with SNR = 20dB, 5 synchronous users, 31 Gold
Codes, and -10dB weaken user and variable step-size

30. Robust CMA with QI Constraint
QC Robust MUD
 H 2 
( ) C 1H f = g f aH f a ≤ β 2
2
min J1 ( f )  E  f x − r  S.T. &
LCCMA1
f
 

( 
) f aH f a ≤ β 2
2
min J ( f a )  E  ( f c − Bf a ) x − r  S.T.
H 2
fa
 
min J 2 (f )  E
f
{(f H x − r )
2
} S.T. C 1H f = g & f aH f a ≤ β 2
LCCMA2 J 2 (f )  −f H E {rx } + f H E {x x H } f 
J 2 ( f )  − f H x + f H R ( n) f

min J (f a )  −(f c − Bf a ) H x + (f c − Bf a ) H R (n )(f c − Bf a ) S.T.
fa
f aH f a ≤ β 2
N −1
=Ψ( f )
1
∑  f aH ( j ) Z ( n ) f a ( j ) − 1
 
2
S.T. f aH ( j ) f a ( j ) ≤ β 2
4M n =0
BSCMA
iM −1
Z (i ) = ∑
n= ( i −1) M
z ( n) z T ( n)

31. Simulation Results of Robust CMA
QC Robust MUD
15 5
4
10
3
2
Output SINR (dB)
Output SINR (dB)
5
1
0
0 LCCMA1 w/t W.
LCCMA1 w. W.
-1
LCCMA1 w. VL BSCMA w. VL
LCCMA2 w/t QI BCGCMA w. VL
-5 LCCMA2 w. SP -2
BGDCMA w. VL
LCCMA2 w. VL
BSCMA
LCCMA2 w. CG -3
BCGCMA
BGDCMA
-10 -4
0 100 200 300 400 500 600 700 800 900 1000 0 50 100 150 200 250
Iterations (n) Block Iteration (j)
Output SINR for Different LCCMA receivers Output SINR for BSCMA receivers with SNR =
with SNR = 30dB, 5 synchronous users, 31 30dB, 5 synchronous users, 31 Gold Codes,
Gold Codes, and -10dB weaken user and -10dB weaken user

32. Agenda
Introduction
Numerically Robust Multiuser Receivers
Quadratically Constrained Robust MUD
Robust Adaptive Beamforming
Thesis Contributions & Publications

33. LCMV Beamforming
Robust Beamforming
 Adaptive beamforming has been exploited in wireless communications,
radar, sonar, speech processing, and other areas.
 Recently, there has been a great effort to design robust adaptive
beamforming techniques which improve robustness against mismatch and
modeling errors and enhancing interference cancellation capability.
 The mismatch may be caused by uncertainty in direction-of-arrival (DOA),
imperfect array calibration, near-far effect, and other mismatch and modeling
errors.
 The so-called linearly constrained minimum variance (LCMV) beamformer,
also known as Capon’s method, has bean a popular beamforming technique.
 In LCMV beamforming method, the weights are chosen to minimize
the array output power subject to side constraint (s) in the desired
look direction (s).
Rxx1a0 (θ 0 )
−
minw R xx w S. T. w a0 (θ0 ) = 1 w0 = H
H H
w a0 (θ 0 ) Rxx1a0 (θ 0 )
−
 This method assumes that the array manifold is accurately known,
unfortunately, even small discrepancy between the presumed and the actual
array manifold can substantially degrade its performance.

34. Diagonal Loading Technique
Robust Beamforming
 Diagonal loading is a technique where the diagonal of the
covariance matrix is augmented with a positive or negative constant
prior to inversion
 Diagonal loading technique has been a widespread approach to
improve robustness against mismatch errors and random
perturbations
 Moreover, the performance of the signal detectors, which utilize the
inverse of the data covariance matrix, experiences serious
degradation when the sample support available for estimating the
matrix is limited.
 This problem can be overcome also by diagonally loading the data
covariance matrix
 Furthermore, it is well known that antenna sidelobes can be made
small if the sample data correlation matrix is diagonally loaded
before inversion is performed

35. Robust Beamforming Design
Robust Beamforming
min w H R xx w
w
S.T. w Hc ≥1 ∀c ∈ A (ε ) A (ε ) = | c = + e , e ≤ ε }
{c a0
SOCP Approach
H
min w R xx w S.T. w H a0 ≥ ε w + 1 & Im {w H a 0 } = 0
w
 The SOCP approach can be interpreted as a diagonal
loading technique in which the optimal value of diagonal
loading is computed based on the known upper bound on the
norm of the signal steering vector mismatch
 The SeDuMe optimization Matlab toolbox has been used to
compute the weight vector of SCOP approach.
 Unfortunately, the computational burden of this software
seems to be cumbersome which limits the practical
implementation of this technique.
 The SOCP-based method does not provide any closed-from
solution, and does not have simple on-line implementations
 In addition, this technique can be regarded as batch
algorithm rather than adaptive scheme.

36. Robust Beamforming Design (2)
Robust Beamforming
Ellipsoidal max min w H Rxx w S.T. w H a0 (θ0 ) = 1 & (a0 (k ) − a0 ) H C −1 (a0 (k ) − a0 ) ≤ 1
ˆ ˆ ˆ
ˆ
a0 w
Constraint S.T. where 1
ˆ H
ˆ −1
min a (k )R (k )a0 (k ) a 0 (k ) − a0 ≤ ε
ˆ
2
C −1 = I
ˆ
a
0 xx
ε
 R (k ) 
−1 −1 Rxx1a0 (θ 0 )
−
ˆ M
zm
2
+ I  a0 w0 = H
ˆ g (λ )  ∑ = ε z = U H a R ΓU
xx = U
xx
a0 
ˆ a0 (θ 0 ) Rxx a0 (θ 0 )
−1
H
ˆ ˆ j =1 (1 + λγ m )
2
 λ
0

 Eigendecomposition requires high computational burden of order O (M 3 )
 The adaptive implementation updates both the covariance matrix and its
inverse to compute the diagonal loading value and the robust detector
 This technique is based on batch algorithm
 The rank of signal and noise may be uncertain or not exactly known and
need to be estimated in advance.
 The covariance matrix will be always diagonally loaded even without
mismatch.

37. Proposed Formulation
Robust Beamforming
Cost Function Ψ aˆ (k ) ˆ ˆ
λ
= a0H (k ) Rxx1 (k )a0 (k ) + t a0 (k ) − a0 − ε
−
2
ˆ
2
( )
a0 (k= a0 (k − 1) − µ SD (k ) g (k ) α g H (k ) g (k ) Step-Size
ˆ ) ˆ µ SD (k ) =
g H (k ) Rxx1 (k ) g (k ) +=
−
σ g (k ) Rxx1 ( k )a0 ( k − 1) + λ ( a0 ( k − 1) − a0 )
−
ˆ ˆ
Steering Vector Update Gradient Vector
a0 (k= a0 (k − 1) − µ SD (k ) ( Rxx1 (k )a0 (k − 1) + λ (k ) ( a0 (k − 1) − a0 ) ) a0 (k= a0 (k − 1) − µ SD (k ) Rxx1 (k )a0 (k − 1)
−
ˆ ) ˆ −
ˆ ˆ  ) ˆ ˆ
Spherical Constraint
(( a (k ) − µ (k )λ (k ) ( a0 (k − 1) − a0 ) ) − a0 ) (( a (k ) − µ )
(k )λ (k ) ( a0 (k − 1) − a0 ) ) − a0 ≤ ε
H
0 SD
ˆ 0 SD
ˆ
Diagonal Loading Term b1 ± b12 − a1c1
λ (k ) =
a1
a1 µ SD (k ) a0 (k − 1)=
− a0 > 0 b1 µ SD (k ) Re {( a0 (k ) − a0 ) ( a0 (k − 1) − a0 )} = a0 (k ) − a0 − ε > 0
c1 
2 2

2 H
ˆ ˆ
Step-Size Constraint b12 − a1c1 ≥ 0

d 0 (k − 1)   Re {d 0 (k − 1)} , Im {d 0 (k − 1)} 
T T
 2      
 d (k − 1) 2 g (k ) 2 − g H (k )d (k − 1)d (k − 1) H g (k )   
µSD ≤ ε d 0 (k − 1)
 0
 0 0 
 
g (k ) =  Re { g (k )} , Im { g (k )} 
T T
 

38. Geometric Approach
Robust Beamforming
2
d 0 (k ) µ (k )λ (k ) ( a0 (k − 1) − a )
ˆ
d 0 (k )
Array broadside
1 C
ε O
B
d 0 (k − 1) D A

a 0 (k )
ˆ
a0 (k )
a 0 (k + 1)
ˆ
a Array direction
Q
Geometric Representation for Robust Capon
Beamforming with ellipsoidal constraint

39. Joint Constraint Approach
Robust Beamforming
 L   H L 
ˆ ˆ
max w Rxx w0 H
=s s ∑R i
Rρ H
+ n max  wρ ∑ w i
ˆ0 s s i i
H
ˆ 0w σw ˆ 0 ˆ 0 
+ 2 H
0
 
xx i i
 i=1 
ˆ
a0
ˆ
a0 i =1
ˆH ˆ
max min w0 Rxx w0 S.T. w0 a0 (θ 0 ) = 1
ˆH ˆ & w0 w0 ≤ τ
ˆH ˆ & a 0 (k ) − a0
ˆ
2
≤ε
ˆ
a0 ˆ
w0
−1
 Rxx1 (k )
−

= 
ˆ
a0 + I  a0
 λ 
( Rxx + υ I ) a0 (k ) ( Rxx + υ I )
−1 −1
( R + υ I ) Rxx ( Rxx + I λ ) a0
−1 −1
ˆ  ˆ
a0 ( k ) 

w0 = w0 = w0 = H xx
a0 (k ) ( Rxx + I λ ) Rxx ( Rxx + I λ ) a0
−1 −1
a0H (k ) ( Rxx + υ I ) a0 (k )
−1 −
ˆ ˆ a0H (k ) Rxx1a0 (k )
ˆ ˆ
 ( I + υ R ) Rxx a0 (k ) ( I −υ R ) R 
−1 −1
−1 −1 −1
ˆ
w0 = −
xx 
w0 ≈
xx
ˆ
a (k )
xx 0 w0 ≈ w0 − υ w0 w0 = Rxx1w0
ˆ −
ˆ
−
a0H (k ) Rxx1a0 (k )
ˆ ˆ a0H (k ) Rxx1a0 (k )
ˆ ˆ

40. Simulation Scenario
Robust Beamforming
Actual DOA
Jammer 1 Direction
Presumed DOA Jammer 2 direction
ϕ1
Mismatch angle 0.03π
λ ϕ2
2
Signal processor
w1 Control algorithm
w1
Beamformer w1
w1
w1 Adaptive processor
∑
Array Output

41. Simulation Results (SINR)
Robust Beamforming
15 25
10
20
5
15
SINR (dB)
0
SINR (dB)
-5
10
-10 Standared Capon
Robust Capon (Batch)
5
Standared Capon Robust Capon (SS)
-15 Robust Capon (Batch) Robust (SOCP)
Robust Capon (SS)
Robust (SOCP)
Proposed1
Proposed1 Proposed2
Proposed2 0
-20
0 100 200 300 400 500 600 700 800 900 1000 0 100 200 300 400 500 600 700 800 900 1000
Iterations (n) Iterations (n)
Output SINR versus snapshot for SNR =20 dB, Output SINR versus snapshot for SNR =40 dB,
two 10dB interference, 0.3pi mismatch angle two 10dB interference, 0.3pi mismatch angle

42. Simulation Results (Beampatterns)
Robust Beamforming
0
-10
-20
-30
-40
Standared Capon
-50 Robust Capon (Batch)
Robust Capon (SS)
Robust (SOCP)
Proposed
-60
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
Angle (radian)
steady state beampatterns for versus snapshot for SNR
=40 dB, two 10dB interference, 0.3pi mismatch angle

43. Simulation Results (Moving Interference)
Robust Beamforming
20
25
18
16 20
14
12 15
SINR (dB)
SINR (dB)
10
8 10
6
4 5
Standared Capon
Standared Capon
Robust Capon (Batch)
Robust Capon (Batch)
2 Robust Capon (SS)
Robust Capon (SS)
Robust (SOCP)
Robust (SOCP)
Proposed Proposed
0
0 100 200 300 400 500 600 700 800 900 1000 0
0 100 200 300 400 500 600 700 800 900 1000
Iterations (n)
Iterations (n)
Output SINR versus snapshot for SNR Output SINR versus snapshot for SNR =20
=20 dB, two coherent moving 10dB dB, two moving 10dB interference, 0.3pi
interference, 0.3pi mismatch angle mismatch angle

44. Agenda
Introduction
Numerically Robust Multiuser Receivers
Quadratically Constraint Robust MUD
Robust Adaptive Beamforming
Thesis Contributions & Publications

45. Contributions Summary (1)
Contributions &Publications
• A general DS/CDMA system model which account for
asynchronism, multipath propagation, near-far effect, signature
mismatch, and inter-symbol-interference (ISI) is developed.
• MUD survey and performance comparison for existing techniques
is performed anchored in the proposed model.
• A fast subspace tracking algorithm is Developed and deployed for
channel estimation with MOE detector.
• A generalized frame work for building IQRD-based multiuser
receivers is offered.
• Based on the above proposed frame work, comparative analyses
between the recently proposed channel estimation techniques,
subspace tracking and the proposed techniques is conducted.
• A combined subspace approach and a quadratic constraint is
proposed to produce robust and optimum multiuser receiver.
• The systolic array implementation is exploited to facilitate real-
time implementation of the proposed IQRD-based receivers.

46. Contributions Summery (2)
Contributions &Publications
• A new VL technique is devised in this thesis and integrated into a
recursive steepest descent (RSD) algorithm rather than the RLS
algorithms to produce robust MOE detector with low-computational
complexity. This VL is exploited to fulfill the quadratic constraint on the
detector norm to improve the performance of the multiuser receiver
against modeling and mismatch errors.
• Additionally, an optimum step-size closed-form expression for the
proposed RSD algorithm is derived.
• The proposed VL technique has been integrated also into the LCCMA
algorithms and the BSCMA algorithm to produce robust constant modulus
based receivers for sample-by-sample and block-adaptive, respectively.
• We have proposed a low-complexity recursive implementation for the
robust Capon beamforming algorithm which incorporating ellipsoidal
constraint on the steering vector using the proposed RSD algorithm and
the recursive conjugate gradient (RCG) algorithm.
• Additionally, a joint constraint approach is proposed to produce robust
beamforming algorithm which is capable of providing robustness against
steering vector mismatch and noise enhancement at low SNR.
• A comparative analysis is conducted between most recent beamforming
algorithms as well as the proposed approaches in the presence of moving
and coherent jamming.

47. Publications List (updated on Oct. 2011)
Contributions &Publications
• Major Publications in Refereed Journals:
• A. Elnashar, “On efficient implementation of robust adaptive beamforming based on worst-case
performance optimization” IET Signal Processing, Vol. 2, No. 4, pp. 381-393, Dec. 2008.
• A. Elnashar, S. Elnoubi, and H. Elmikati “Performance Analysis of Blind Adaptive MOE Multiuser
Receivers using Inverse QRD-RLS Algorithm,” IEEE Trans. On Circuits and systems I, Vol. 55, No. 1,
pp. 398-411, Feb. 2008.
• A. Elnashar, S. Elnoubi, and H. Elmikati “Further study on Robust Adaptive Beamforming with optimum
diagonal loading,” IEEE Trans. on Antennas and Propagation, Vol. 54, No 12, pp. 3647-3658, Dec.
2006.
• A. Elnashar, S. Elnoubi, and H. Elmikati, “Low-Complexity Robust Adaptive Generalized Sidelobe
Canceller Detector for DS/CDMA Systems,” International Journal of Adaptive Control and Signal
Processing, vol. 23, no. 3, pp. 293-310,March 2008, John Wiley & Sons, Ltd.
• T. Samir, S. Elnoubi, and A. Elnashar, “Block-Shanno Minimum BER Beamforming,” IEEE transactions
on Vehicular Technology, Vol. 57, No. 5, pp. 2981-2990, Sept. 2008.
• International Conferences:
• T. Samir, S. Elnoubi, and A. Elnashar “Block-Shanno MBER algorithm in a spatial multiuser
MIMO/OFDM” in Proc. 14th European Wireless Conference EW2008, 22-25 June 2008.
• T. Samir, S. Elnoubi, and A. Elnashar “Class of Minimum Bit Error Rate Algorithms,” in Proc. ICACT
2007, Korea, Feb. 2007, pp. 168-173.
• T. Samir, S. Elnoubi, and A. Elnashar, “Block-Shanno Minimum BER Beamforming” in Proc. ISSPA
2007, UAE, Feb. 2007.
• A. Elnashar, “Robust Adaptive Beamforming,” ACE2 Network of Excellence Workshop on Smart
Antennas, MIMO Systems and Related Technologies, Myconos, Greece, 8 June 2006.

48. Publications List (Cont.)
Contributions &Publications
• A. Elnashar, S. Elnoubi, and H. Elmikati, “Performance analysis of robust MOE detectors at low SNR
based on the IQRD-RLS algorithm,” In Proc. IST Mobile and Wireless Communications Summit,
Myconos, Greece, 4-8 June, 2006.
• A. Elnashar, S. Elnoubi, and H. Elmikati “Robust Adaptive Beamforming with Variable Diagonal Loading,”
In Proc. Sixth International Conference on 3G and Beyond - 3G 2005, 07-09 November 2005, The
IEE, Savoy Place, London, UK, pp. 489-493.
• A. Elnashar, S. Elnoubi, and H. Elmikati “A Robust Block-Shanno Adaptive Blind Multiuser Receiver for
DS-CDMA Systems,” In Proc. IST Mobile & Wireless Communications Summit 2005, Dresden, Germany,
19-23 June, 2005.
• A. Elnashar, S. Elnoubi, and H. Elmikati “A Robust Linearly Constrained CMA for Adaptive Blind Multiuser
Detection,” In Proc. IEEE WCNC 2005 conference, Vol. 1, pp. 233-238, New Orleans, LA, USA, 13-17
March, 2005,
• A. Elnashar, S. Elnoubi, and H. Elmikati “A Robust Quadratically Constrained Adaptive Blind Multiuser
Receiver for DS/CDMA Systems,” IEEE International Symposium on Spread Spectrum Techniques and
Applications (ISSSTA 2004), Sydney, Australia 30 Aug 2004 - 3 Sept 2004.
• A. Elnashar, S. Elnoubi, and H. Elmikati “A Novel Adaptive Blind Multiuser Receiver for DS/CDMA Based
on combined Inverse QRD-RLS Algorithm and constrained Optimization Approach,” in Proc. ISPACS
2003, Awaji Island, Japan, pp. 423-428, December 7-10, 2003.
• A. Elnashar, S. Elnoubi, and H. Elmikati “Computationally Efficient Real-Time Blind Multiuser Detection for
cellular DS/CDMA Based on Inverse QRD-RLS Algorithm and Subspace Tracking,” in Proc. MWSCAS
2003, Cairo, Egypt, December 28-31, 2003.
• A. Elnashar, S. Elnoubi, and H. Elmikati “Robust Adaptive Blind Multiuser Receiver for DS/CDMA Based
on combined Inverse QRD-RLS Algorithm and MOE” in Proc. SOFTCOM 2003 conference, Croatia, pp.
512-515, Oct. 2003.