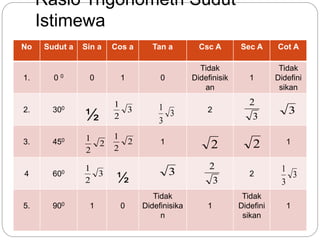
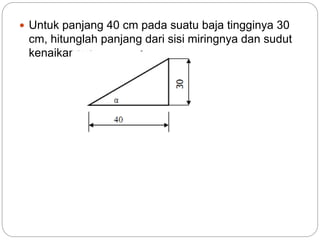
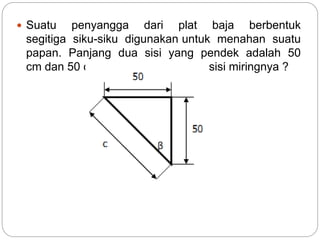
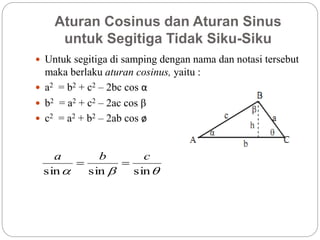
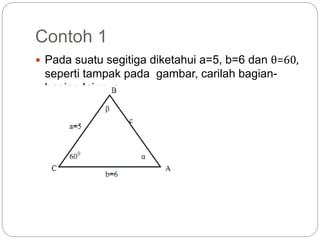
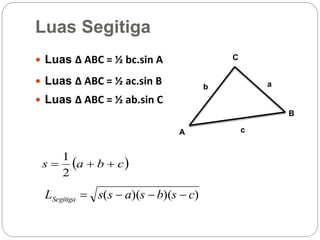
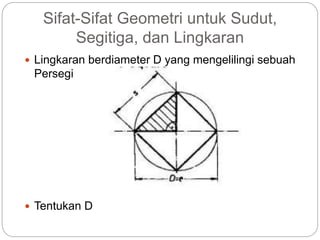
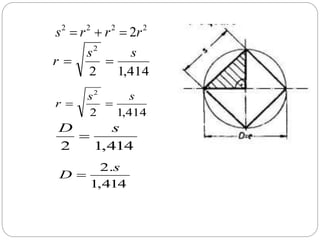
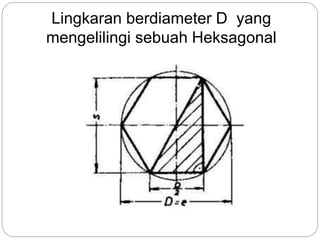
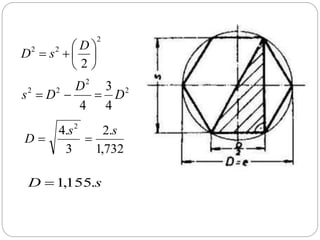
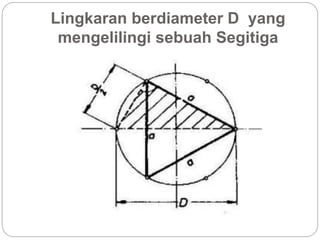
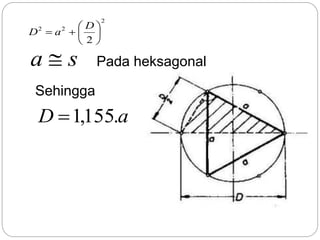
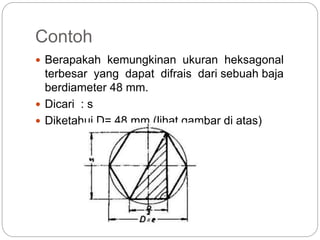
Dokumen ini membahas rasio trigonometri dan aplikasi teorema dalam segitiga, termasuk besaran sudut dan panjang sisi. Ini mencakup contoh penggunaan teorema Pythagoras dan aturan sinus serta cosinus untuk menghitung panjang dan sudut dalam segitiga. Selain itu, dokumen juga membahas sifat geometri lingkaran dan heksagon yang berhubungan dengan diameter.

1. INDAH RIEZKY PRATIWI
TRIGONOMETRI

2. RASIO TRIGONOMETRI
c
a
SinA 
c
b
CosA 
b
a
TanA
TanAa
b
CotA
1

CosAb
c
SecA
1

SinAa
c
CscA
1


3. Rasio Trigonometri Sudut
Istimewa
No Sudut a Sin a Cos a Tan a Csc A Sec A Cot A
1. 0 0 0 1 0
Tidak
Didefinisik
an
1
Tidak
Didefini
sikan
2. 300
½ 2
3. 450 1 1
4 600
½ 2
5. 900 1 0
Tidak
Didefinisika
n
1
Tidak
Didefini
sikan
1
3
3
1
3
2
3
2
2
1
3
3
2
1
3
2
1
2
2
1
2
3
2
2
3
3
1

4.  Untuk panjang 40 cm pada suatu baja tingginya 30
cm, hitunglah panjang dari sisi miringnya dan sudut
kenaikannya .

5. Jawab
 Ditanyakan: L dan α
 Diketahui : l = 40 cm dan h = 30 cm
 tan α = 75,0
40
30

l
h

6.  Suatu penyangga dari plat baja berbentuk
segitiga siku-siku digunakan untuk menahan suatu
papan. Panjang dua sisi yang pendek adalah 50
cm dan 50 cm. Berapakah panjang sisi miringnya ?

7. Jawab
 Panjang dua sisi yang lain a=b=50
Penyelesaian :
 Perhitungan dengan teorema
 Phytagoras
c2 = a2 + b2
c2 = 502 + 502
c = cm71,70250 

8. Aturan Cosinus dan Aturan Sinus
untuk Segitiga Tidak Siku-Siku
 Untuk segitiga di samping dengan nama dan notasi tersebut
maka berlaku aturan cosinus, yaitu :
 a2 = b2 + c2 – 2bc cos α
 b2 = a2 + c2 – 2ac cos β
 c2 = a2 + b2 – 2ab cos ø
 sinsinsin
cba


9. Contoh 1
 Pada suatu segitiga diketahui a=5, b=6 dan θ=60,
seperti tampak pada gambar, carilah bagian-
bagian lainnya.

10.  Diketahui : Segitiga dengan notasi dan ukuran pada
gambar.
 Ditanyakan : c , α ,
 Jawab :
 C dapat dicari dengan aturan cosinus :
c2 = a2 + b2 – 2ab cos α
c2 = 52 + 62 – 2.5.6 cos 600
c2 = 61 – 60. ( ½ ) = 31
c =

6,531 

11.  Aturan cosinus dapat pula digunakan untuk
mendapat α :
 a2 = b2 + c2 – 2bc cos α
 α = 51,3170
 Sudut β dapat dicari juga dengan aturan cosinus. Akan
tetapi karena kita tahu bahwa jumlah sudut pada suatu segitiga
adalah 1800, maka
 β = 1800 – 600 – 51,3170 = 68,683o
6250,0
)6,5)(6(2
253136
2
222





bc
acb
Cos

12. Luas Segitiga
A
B
 Luas ∆ ABC = ½ bc.sin A C
c
b a Luas ∆ ABC = ½ ac.sin B
 Luas ∆ ABC = ½ ab.sin C
 cbas 
2
1
))()(( csbsassLSegitiga 

13. Sifat-Sifat Geometri untuk Sudut,
Segitiga, dan Lingkaran
 Lingkaran berdiameter D yang mengelilingi sebuah
Persegi
 Tentukan D

14. 2222
2rrrs 
414,12
2
ss
r 
414,12
2
ss
r 
414,12
sD

414,1
.2 s
D 

15. Lingkaran berdiameter D yang
mengelilingi sebuah Heksagonal

16. 2
22
2







D
sD
2
2
22
4
3
4
D
D
Ds 
732,1
.2
3
.4 2
ss
D 
sD .155,1

17. Lingkaran berdiameter D yang
mengelilingi sebuah Segitiga

18. 2
22
2







D
aD
sa  Pada heksagonal
Sehingga
aD .155,1

19. Contoh
 Berapakah kemungkinan ukuran heksagonal
terbesar yang dapat difrais dari sebuah baja
berdiameter 48 mm.
 Dicari : s
 Diketahui D= 48 mm (lihat gambar di atas)