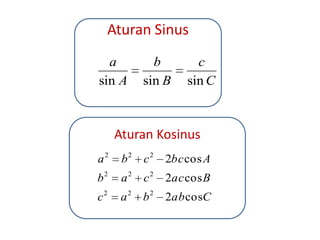
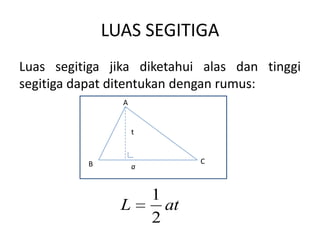
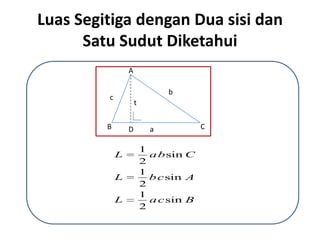
Dokumen tersebut membahas tentang rumus-rumus untuk menghitung luas segitiga dengan berbagai kondisi yang diketahui, seperti alas dan tinggi segitiga, dua sisi dan satu sudut, dua sudut dan satu sisi, dua sisi dan sudut di hadapan salah satu sisi, serta ketiga sisinya. Juga dijelaskan cara penyelesaian contoh soal untuk menerapkan rumus-rumus tersebut.

1. LUAS SEGITIGA

2. Aturan Sinus
a b c
sin A sin B sin C
Aturan Kosinus
a2 b2 c2 2bc cos A
b2 a2 c2 2ac cos B
c2 a2 b2 2ab cosC

3. LUAS SEGITIGA
Luas segitiga jika diketahui alas dan tinggi
segitiga dapat ditentukan dengan rumus:
A
t
B C
a
1
L at
2

4. Luas Segitiga dengan Dua sisi dan
Satu Sudut Diketahui
A
b
c
t
B D a C
1
L a b sin C
2
1
L b c sin A
2
1
L a c sin B
2

5. Luas Segitiga dengan Dua sudut dan
Satu Sisi Diketahui.
2
a sin B sin C
L
2 sin A
2
b sin A sin C
L
2 sin B
2
c sin A sin B
L
2 sin C

6. Luas Segitiga dengan Dua sisi dan Sebuah Sudut
di Hadapan Sisi Diketahui.
• Langkah 1:
Tentukan besar sudut – sudut yang belum diketahui
dengan memakai aturan sinus.
• Langkah 2:
Setelah semua sudut diketahui, hitunglah luas
segitiga dengan menggunakan salah satu dari rumus
1 1 1
L ab sin C , L bc sin A, L ac sin B
2 2 2

7. Luas Segitiga dengan Dua sisi dan Sebuah
Sudut di Hadapan Sisi Diketahui.
Luas segitiga ABC jika diketahui panjang ketiga
sisinya (sisi a, sisi b, dan sisi c) dapat ditentukan
dengan rumus:
L s(s a)(s b)(s c)
Dengan s = (a + b + c) = setengah keliling ∆ABC

8. Contoh Soal
1. Dalam ∆ABC, diketahui panjang sisi a = 4 cm,
sisi b = 6 cm,dan besar C = 30°. Hitunglah
luas ∆ABC itu.
Jawab: 1
L ab sin C
2
1
L (4)(6) sin 30
2
1 1
L (4)(6)
2 2
L 6
Jadi, luas ∆ABC adalah L = 6 cm²

9. 2. Dalam ∆ABC, diketahui panjang sisi a= 5 cm, panjang
sisi b = 6 cm, dan panjang sisi c = 7 cm. hitunglah luas
∆ABC.
jawab:
Setengah keliling ∆ABC adalah s = ½(a+b+c)=½(5+6+7)=9
(s-a) = (9 – 5) = 4; (s – b) = (9 – 6) = 3; dan (s – c)=(9-7)=2
L s(s a)(s b)(s c)
L 9( 4)(3)(2)
L 6 6
Jadi, luas ∆ABC sama dengan 6 6cm2

10. Thank
you