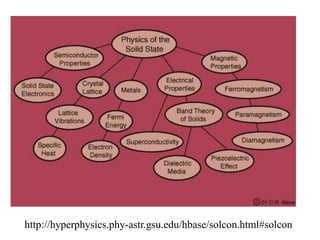
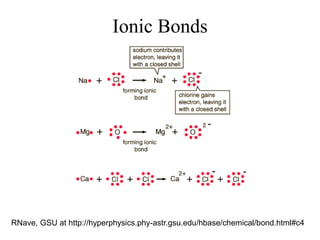
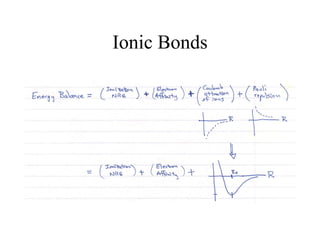
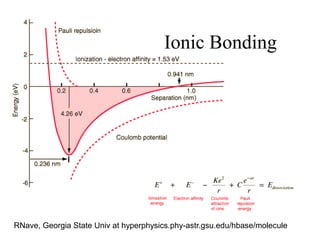
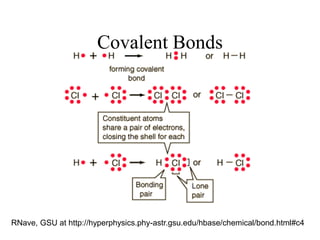
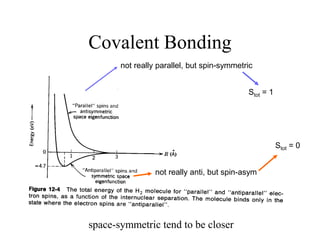
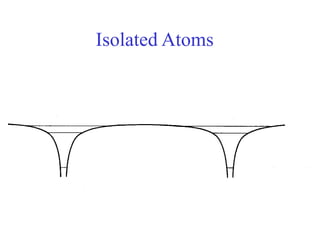
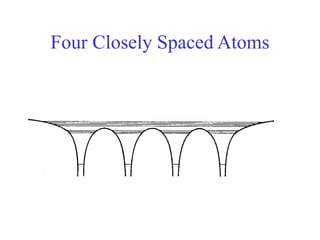
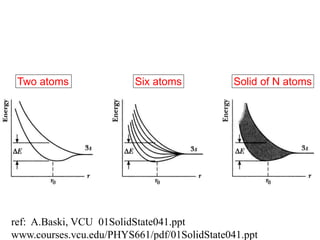
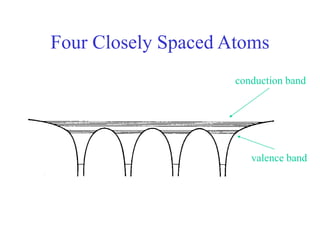
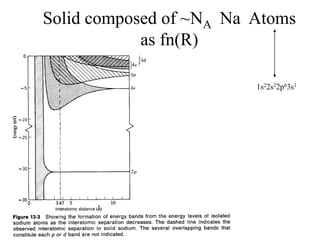
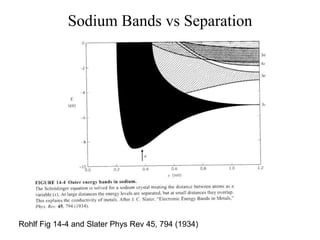
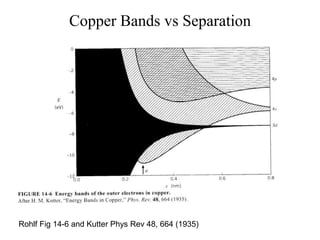
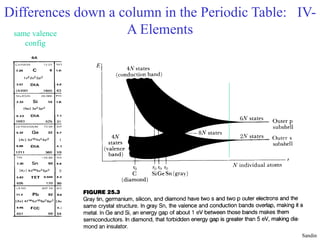
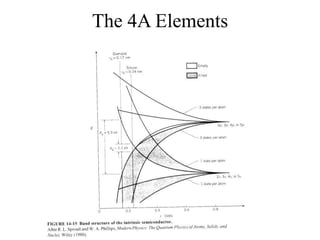
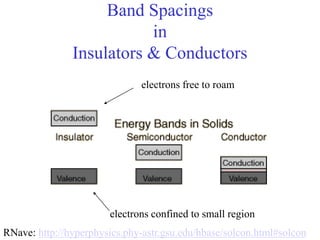
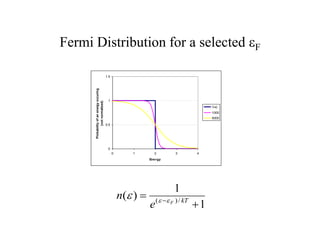
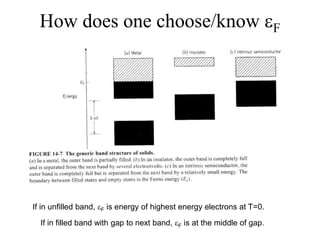
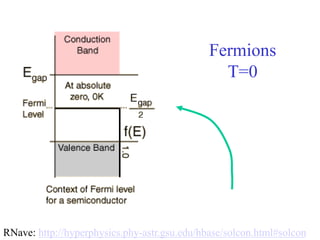
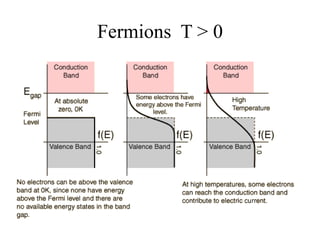
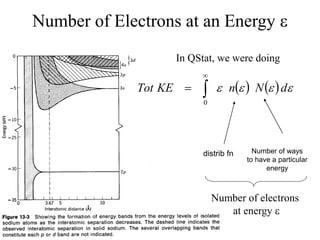
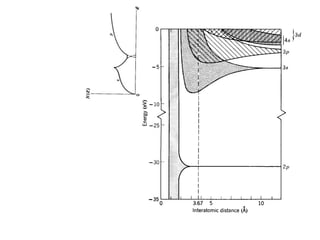
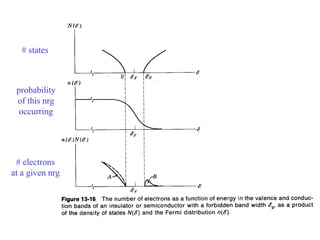
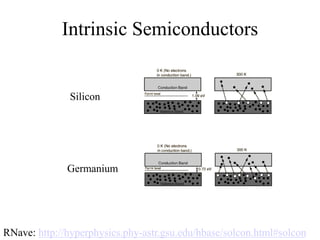
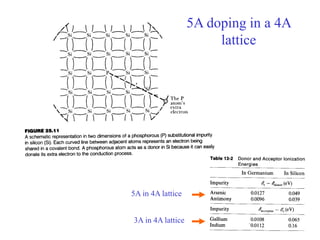
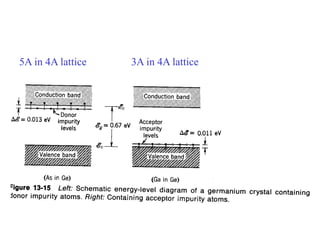
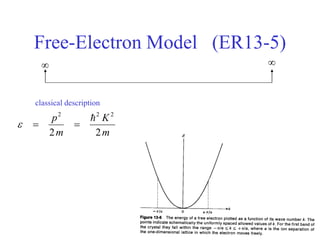
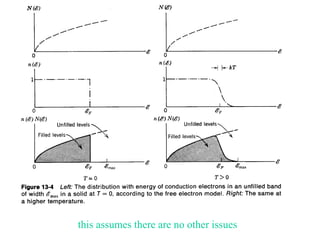
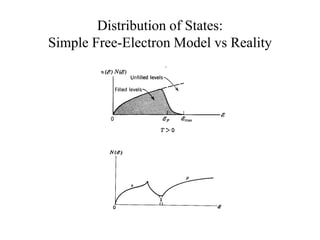
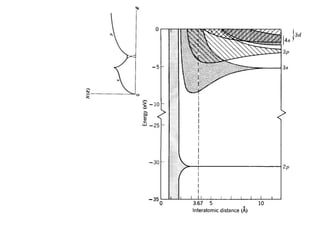
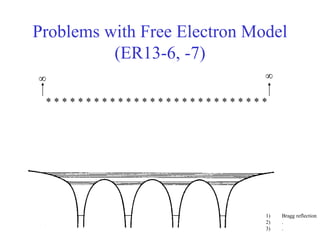
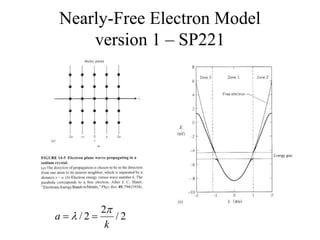
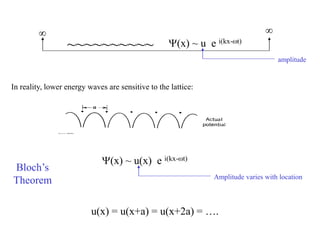
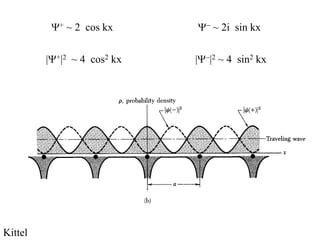
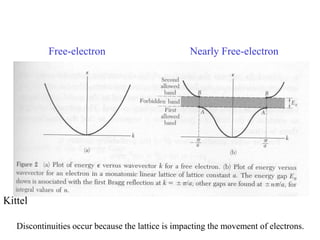
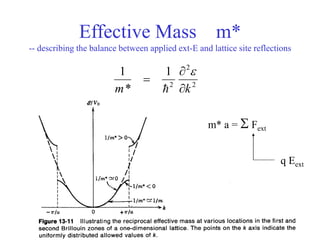
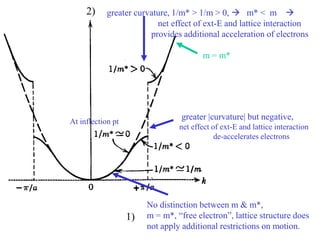
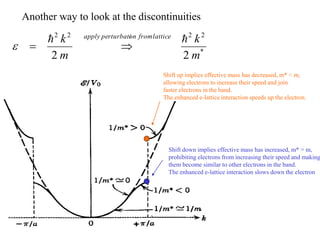
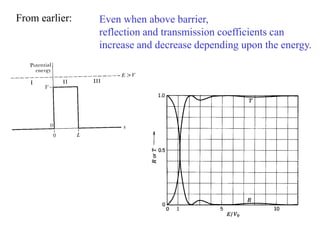
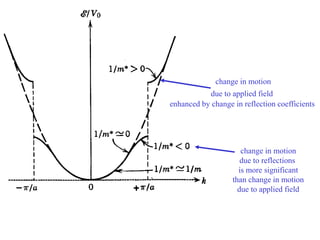
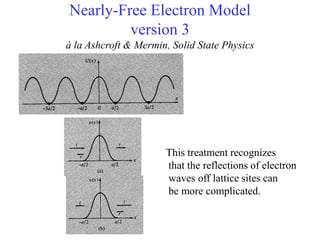
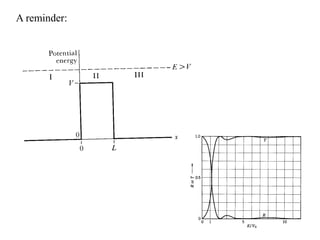
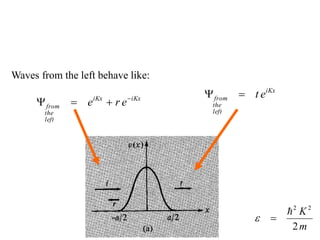
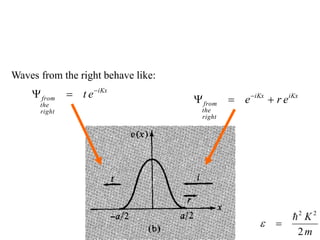
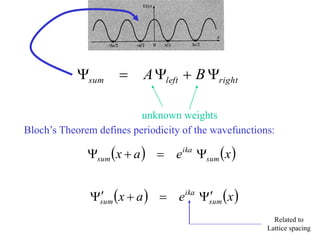
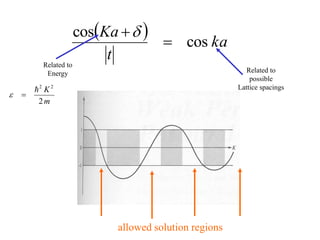
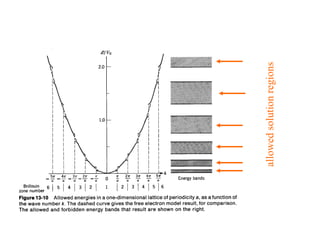
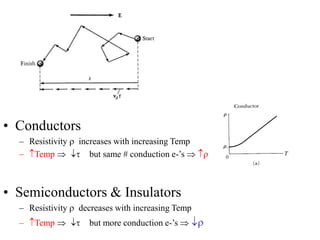
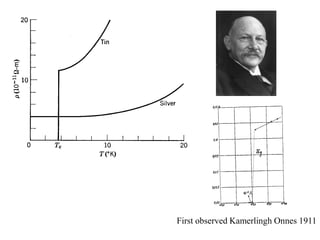
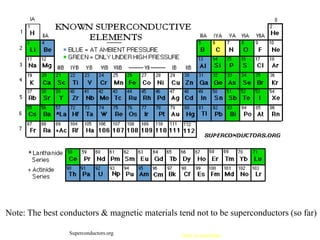
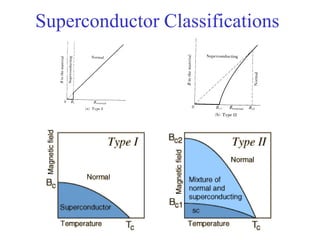
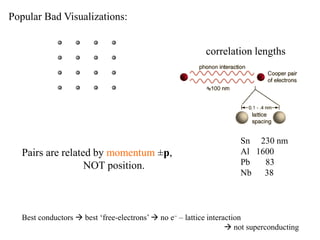
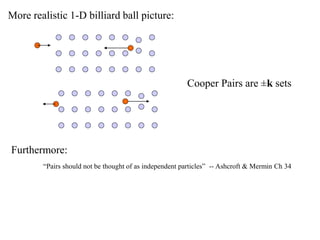
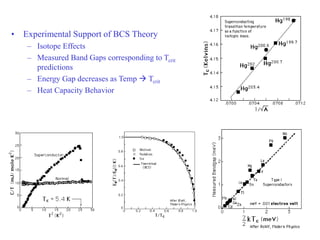
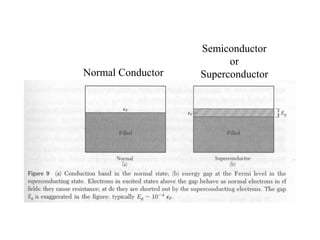
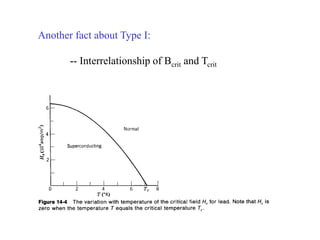
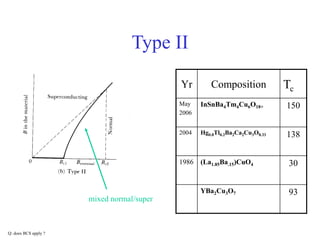
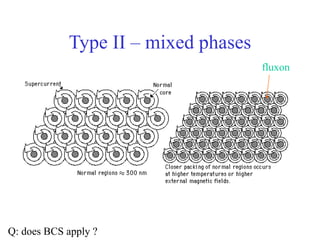
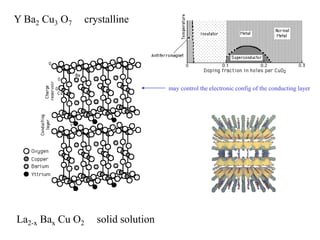
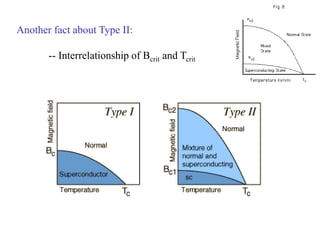
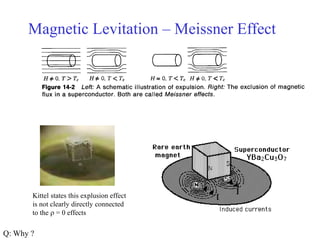
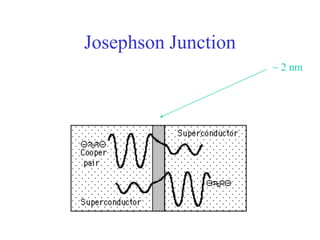
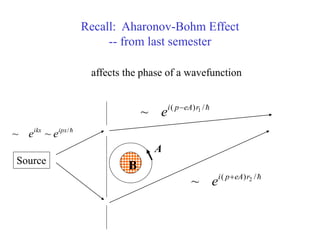
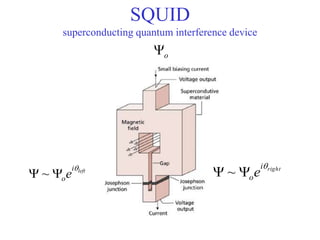
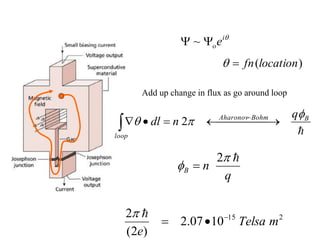
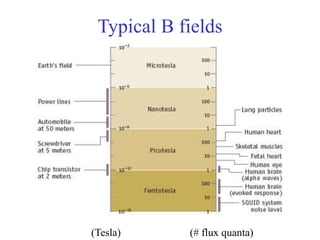
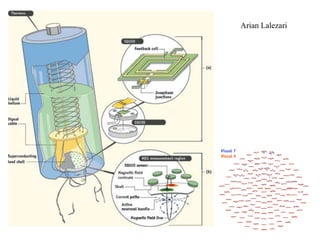
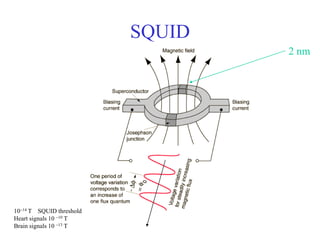
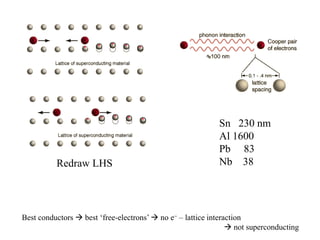
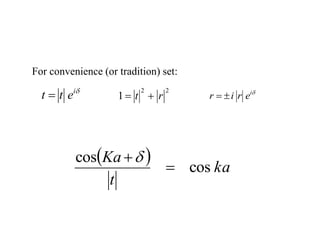This document provides an outline and overview of solid state physics concepts including ionic and covalent bonding, types of solids, band theory, and free electron models. Band theory describes how the energy levels of isolated atoms combine and split into allowed energy bands as atoms are brought together in a solid. Key concepts covered include the formation of valence and conduction bands, density of states, and Fermi energy. Free electron models are discussed as approximations to describe conduction in metals, along with limitations like Bragg reflection. The nearly-free electron model incorporates effects of the periodic lattice potential through concepts like Bloch waves and effective mass.

1. Solids
Eisberg & Resnick Ch 13 & 14
RNave:
http://hyperphysics.phy-astr.gsu.edu/hbase/solcon.html#solcon
Alison Baski:
http://www.courses.vcu.edu/PHYS661/pdf/01SolidState041.ppt
Carl Hepburn, “Britney Spear’s Guide to Semiconductor Physics”.
http://britneyspears.ac/lasers.htm

2. http://hyperphysics.phy-astr.gsu.edu/hbase/solcon.html#solcon

3. OUTLINE
• Review Ionic / Covalent Molecules
• Types of Solids (ER 13.2)
• Band Theory (ER 13.3-.4)
– basic ideas
– description based upon free electrons
– descriptions based upon nearly-free electrons
• ‘Free’ Electron Models (ER 13.5-.7)
• Temperature Dependence of Resistivity (ER 14.1)

4. Ionic Bonds
RNave, GSU at http://hyperphysics.phy-astr.gsu.edu/hbase/chemical/bond.html#c4

5. Ionic Bonds

6. Ionic Bonding
RNave, Georgia State Univ at hyperphysics.phy-astr.gsu.edu/hbase/molecule

7. Covalent Bonds
RNave, GSU at http://hyperphysics.phy-astr.gsu.edu/hbase/chemical/bond.html#c4

8. Covalent Bonding
SYM ASYM
spatial spin
ASYM SYM
spatial spin
space-symmetric tend to be closer

9. Covalent Bonding
Stot = 1
not really parallel, but spin-symmetric
not really anti, but spin-asym
Stot = 0
space-symmetric tend to be closer

11. TYPES OF SOLIDS (ER 13.2)
CRYSTALINE BINDING
• molecular
• ionic
• covalent
• metallic

12. Molecular Solids
• orderly collection of molecules held together by v. d. Waals
• gases solidify only at low Temps
• easy to deform & compress
• poor conductors
most organics
inert gases
O2 N2 H2

13. Ionic Solids
• individ atoms act like closed-shell, spherical, therefore binding
not so directional
• arrangement so that minimize nrg for size of atoms
• tight packed arrangement  poor thermal conductors
• no free electrons  poor electrical conductors
• strong forces  hard & high melting points
• lattice vibrations absorb in far IR
• to excite electrons requires UV, so ~transparent visible
NaCl
NaI
KCl

14. Covalent Solids
• 3D collection of atoms bound by shared valence
electrons
• difficult to deform because bonds are directional
• high melting points (b/c diff to deform)
• no free electrons  poor electrical conductors
• most solids adsorb photons in visible  opaque
Ge Si
diamond

15. Metallic Solids
• (weaker version of covalent bonding)
• constructed of atoms which have very weakly
bound outer electron
• large number of vacancies in orbital (not enough
nrg available to form covalent bonds)
• electrons roam around (electron gas )
• excellent conductors of heat & electricity
• absorb IR, Vis, UV  opaque
Fe Ni Co
config dhalf full

17. BAND STRUCTURE

18. Isolated Atoms

19. Diatomic Molecule

20. Four Closely Spaced Atoms

21. Six Closely Spaced Atoms
as fn(R)
the level of interest
has the same nrg in
each separated atom

22. Solid of N atoms
Two atoms Six atoms
ref: A.Baski, VCU 01SolidState041.ppt
www.courses.vcu.edu/PHYS661/pdf/01SolidState041.ppt

23. Four Closely Spaced Atoms
valence band
conduction band

24. Solid composed of ~NA Na Atoms
as fn(R)
1s22s22p63s1

25. Sodium Bands vs Separation
Rohlf Fig 14-4 and Slater Phys Rev 45, 794 (1934)

26. Copper Bands vs Separation
Rohlf Fig 14-6 and Kutter Phys Rev 48, 664 (1935)

27. Differences down a column in the Periodic Table: IV-
A Elements
Sandin
same valence
config

28. The 4A Elements

29. Band Spacings
in
Insulators & Conductors
electrons free to roam
electrons confined to small region
RNave: http://hyperphysics.phy-astr.gsu.edu/hbase/solcon.html#solcon

30. How to choose eF
and
Behavior of the Fermi function at
band gaps

31. Fermi Distribution for a selected eF
0
0.5
1
1.5
0 1 2 3 4
Energy
Probability
of
an
energy
occuring
(not
normalized)
T=0
1000
5000
1
1
)
( /
)
(

  kT
F
e
n e
e
e

32. How does one choose/know eF
If in unfilled band, eF is energy of highest energy electrons at T=0.
If in filled band with gap to next band, eF is at the middle of gap.

33. Fermions
T=0
RNave: http://hyperphysics.phy-astr.gsu.edu/hbase/solcon.html#solcon

34. Fermions T > 0

35. Number of Electrons at an Energy e
    e
e
e
e d
N
n
KE
Tot 


0
distrib fn Number of ways
to have a particular
energy
In QStat, we were doing
Number of electrons
at energy e

37. # states
probability
of this nrg
occurring
# electrons
at a given nrg

39. Semiconductors
ER13-9, -10

40. Semiconductors
• Types
– Intrinsic – by thermal excitation or high nrg photon
– Photoconductive – excitation by VIS-red or IR
– Extrinsic – by doping
• n-type
• p-type
•
~1 eV
~1/40 eV

41. Intrinsic Semiconductors
Silicon
Germanium
RNave: http://hyperphysics.phy-astr.gsu.edu/hbase/solcon.html#solcon

42. Doped Semiconductors
lattice
p-type dopants n-type dopants

43. 5A in 4A lattice
3A in 4A lattice
5A doping in a 4A
lattice

44. 5A in 4A lattice 3A in 4A lattice

46. ‘Free-Electron’ Models
• Free Electron Model (ER 13-5)
• Nearly-Free Electron Model (ER13-6,-7)
– Version 1 – SP221
– Version 2 – SP324
– Version 3 – SP425
• .

47. • Free-Electron Model
– Spatial Wavefunctions
– Energy of the Electrons
– Fermi Energy
– Density of States dN/dE E&R 13.5
– Number of States as fn NRG E&R 13.5
• Nearly-Free Electron Model (Periodic Lattice Effects) – v2 E&R 13.6
• Nearly-Free Electron Model (Periodic Lattice Effects) – v3 E&R 13.6
 
*********************************************************

48. Free-Electron Model (ER13-5)
 
m
K
m
p
2
2
2
2
2



e
classical description

49.  






 E
m
0
2
2
2

  z
k
y
k
x
k
L
xyz z
y
x sin
sin
sin
8
3




In a 3D slab of metal, e’s are free to move
but must remain on the inside
Solutions are of the form:
L
nz 
 
2
2
2
2
2
8
z
y
x n
n
n
mL
h



e
With nrg’s:
Quantum Mechanical Viewpoint

50. At T = 0, all states are filled
up to the Fermi nrg
 max
2
2
2
2
2
8
z
y
x
fermi n
n
n
mL
h



e
A useful way to keep track of the states that are filled is:
max
2
2
2
2
n
n
n
n z
y
x 



51. total number of states up to an energy efermi:
3
3
max
4
8
1
8
1
2
2
n
sphere
of
volume 








N
3
/
2
2
3
8 








V
N
m
h
fermi

e
max
2
2
2
8
n
mL
h
fermi 
e
# states/volume ~ # free e’s / volume

52. Sample Numerical Values for Copper slab
V
N
= 8.96 gm/cm3 1/63.6 amu 6e23 = 8.5e22 #/cm3 = 8.5e28 #/m3
efermi = 7 eV
3
/
2
2
3
8 








V
N
m
h
fermi

e
nmax = 4.3 e 7
so we can easily pretend that there’s a smooth distrib of nxnynz-states

53. Density of States
How many combinations of are there
within an energy interval e to e + de ?
3
/
2
2
3
8 








V
N
m
h
fermi

e
2
/
3
2
8
3













h
mE
V
N

dE
h
m
h
mE
V
dN 2
2
/
1
2
8
8
2
3
3














  2
/
1
2
/
1
3
3
2
8
E
m
h
V
dE
dN 

    e
e
e
e d
N
n
KE
Tot 


0

54. At T ≠ 0 the electrons will be spread out among the allowed states
How many electrons are contained in a particular energy range?
















occuring
energy
this
of
y
probabilit
energy
particular
a
have
to
ways
of
number
 
1
1
2
8
/
)
(
2
/
1
2
/
1
3
3

 kT
E f
e
E
m
h
V
e


55. this assumes there are no other issues

56. Distribution of States:
Simple Free-Electron Model vs Reality

58. Problems with Free Electron Model
(ER13-6, -7)
 
* * * * * * * * * * * * * * * * * * * * * * * * * * * *
1) Bragg reflection
2) .
3) .

59. Other Problems with the Free Electron Model
• graphite is conductor, diamond is insulator
• variation in colors of x-A elements
• temperature dependance of resistivity
• resistivity can depend on orientation of crystal & current I direction
• frequency dependance of conductivity
• variations in Hall effect parameters
• resistance of wires effected by applied B-fields
• .
• .
• .

60. Nearly-Free Electron Model
version 1 – SP221
2
/
2
2
/
k
a

 

2
/


k
2
/
2
2
/
k
a

 


61. Nearly-Free Electron Model
version 2 – SP324
• Bloch Theorem
• Special Phase Conditions, k = +/- m /a
• the Special Phase Condition k = +/- /a
This treatment assumes that when
a reflection occurs, it is 100%.

62. (x) ~ u e i(kx-wt)
(x) ~ u(x) e i(kx-wt)
 
~~~~~~~~~~
amplitude
In reality, lower energy waves are sensitive to the lattice:
Amplitude varies with location
u(x) = u(x+a) = u(x+2a) = ….
Bloch’s
Theorem

63. u(x+a) = u(x)
(x+a) e -i(kx+ka-wt)  (x) e -i(kx-wt)
(x) ~ u(x) e i(kx-wt)
(x+a)  e ika (x)
Something special happens with the phase when
e ika = 1
ka = +/ m  m = 0 not a surprise
m = 1, 2, 3, …
...
,
2
,
a
a
k





What it is ?

64. a
k



Consider a set of waves with +/ k-pairs, e.g.
k = + /a moves  k =  /a moves 
This defines a pair of waves moving right & left
Two trivial ways to superpose these waves are:
+ ~ e ikx + e ikx  ~ e ikx  e ikx
+ ~ 2 cos kx  ~ 2i sin kx

65. + ~ 2 cos kx  ~ 2i sin kx
Kittel
|+|2 ~ 4 cos2 kx ||2 ~ 4 sin2 kx

66. Free-electron Nearly Free-electron
Kittel
Discontinuities occur because the lattice is impacting the movement of electrons.

67. Effective Mass m*
A method to force the free electron
model to work in the situations where
there are complications
ER Ch 13 p461 starting w/ eqn (13-19b)
*
2
2
2
m
k


e
free electron KE functional form

68. Effective Mass m*
-- describing the balance between applied ext-E and lattice site reflections
2
2
2
1
*
1
k
m 


e

m* a = S Fext
q Eext

69. No distinction between m & m*,
m = m*, “free electron”, lattice structure does
not apply additional restrictions on motion.
m = m*
greater curvature, 1/m* > 1/m > 0,  m* < m 
net effect of ext-E and lattice interaction
provides additional acceleration of electrons
greater |curvature| but negative,
net effect of ext-E and lattice interaction
de-accelerates electrons
At inflection pt
1)
2)

70. *
2
2
2
2
2
2 m
k
m
k lattice
from
on
perturbati
apply




e
Another way to look at the discontinuities
Shift up implies effective mass has decreased, m* < m,
allowing electrons to increase their speed and join
faster electrons in the band.
The enhanced e-lattice interaction speeds up the electron.
Shift down implies effective mass has increased, m* > m,
prohibiting electrons from increasing their speed and making
them become similar to other electrons in the band.
The enhanced e-lattice interaction slows down the electron

71. From earlier: Even when above barrier,
reflection and transmission coefficients can
increase and decrease depending upon the energy.

72. change in motion
due to reflections
is more significant
than change in motion
due to applied field
change in motion
due to applied field
enhanced by change in reflection coefficients

73. Nearly-Free Electron Model
version 3
à la Ashcroft & Mermin, Solid State Physics
This treatment recognizes
that the reflections of electron
waves off lattice sites can
be more complicated.

74. A reminder:

75. Waves from the left behave like:
iKx
iKx
left
the
from e
r
e 



iKx
left
the
from e
t


m
K
2
2
2


e

76. Waves from the right behave like:
iKx
iKx
right
the
from e
r
e 

 
iKx
right
the
from e
t 


m
K
2
2
2


e

77. right
left
sum B
A 




Bloch’s Theorem defines periodicity of the wavefunctions:
   
x
e
a
x sum
ika
sum 



   
x
e
a
x sum
ika
sum 



unknown weights
Related to
Lattice spacing

78.    
x
e
a
x sum
ika
sum 


    
x
e
a
x sum
ika
sum 



Applying the matching conditions at x   a/2
A + B
left right
A + B
left right
A + B
left right
A + B
left right
iKa
iKa
e
t
e
t
r
t
ka 



2
1
2
cos
2
2
m
K
2
2
2


e
And eliminating the unknown constants A & B leaves:

79. For convenience (or tradition) set:
2
2
1 r
t 


i
e
t
t  
i
e
r
i
r 

  ka
t
Ka
cos
cos



80.   ka
t
Ka
cos
cos


Related to
possible
Lattice spacings
Related to
Energy
m
K
2
2
2


e
allowed solution regions

81. allowed
solution
regions

82. Superconductivity
ER 14-1, 13-4

83. R Nave: http://hyperphysics.phy-astr.gsu.edu/hbase/solids/supcon.html#c1
Temperature Dependence of Resistivity
Joe Eck: superconductors.org

84. Temperature Dependence of
Resistivity
A
L
R 


85. • Conductors
– Resistivity  increases with increasing Temp
– Temp  t but same # conduction e-’s  
• Semiconductors & Insulators
– Resistivity  decreases with increasing Temp
– Temp  t but more conduction e-’s  

86. First observed Kamerlingh Onnes 1911

87. Superconductors.org Only in nanotubes
Note: The best conductors & magnetic materials tend not to be superconductors (so far)

88. Superconductor Classifications
• Type I
– tend to be pure elements or simple alloys
–  = 0 at T < Tcrit
– Internal B = 0 (Meissner Effect)
– At jinternal > jcrit, no superconductivity
– At Bext > Bcrit, no superconductivity
– Well explained by BCS theory
• Type II
– tend to be ceramic compounds
– Can carry higher current densities ~ 1010 A/m2
– Mechanically harder compounds
– Higher Bcrit critical fields
– Above Bext > Bcrit-1, some superconductivity

89. Superconductor Classifications

90. Type I
Bardeen, Cooper, Schrieffer 1957, 1972
“Cooper Pairs”
Symmetry energy ~ 0.01 eV
Q: Stot=0 or 1? L? J?
e
e

91. Sn 230 nm
Al 1600
Pb 83
Nb 38
Best conductors  best ‘free-electrons’  no e – lattice interaction
 not superconducting
Popular Bad Visualizations:
Pairs are related by momentum ±p,
NOT position.
correlation lengths

92. More realistic 1-D billiard ball picture:
Cooper Pairs are ±k sets
Furthermore:
“Pairs should not be thought of as independent particles” -- Ashcroft & Mermin Ch 34

93. • Experimental Support of BCS Theory
– Isotope Effects
– Measured Band Gaps corresponding to Tcrit
predictions
– Energy Gap decreases as Temp  Tcrit
– Heat Capacity Behavior

94. Normal Conductor
Semiconductor
or
Superconductor

95. Another fact about Type I:
-- Interrelationship of Bcrit and Tcrit

96. Type II
Q: does BCS apply ?
mixed normal/super
Yr Composition Tc
May
2006
InSnBa4Tm4Cu6O18+ 150
2004 Hg0.8Tl0.2Ba2Ca2Cu3O8.33 138
1986 (La1.85Ba.15)CuO4 30
YBa2Cu3O7 93

97. actual ~ 8 mm
Sandin

98. Type II – mixed phases
Q: does BCS apply ?
fluxon

99. Y Ba2 Cu3 O7 crystalline
La2-x Bax Cu O2 solid solution
may control the electronic config of the conducting layer

100. Another fact about Type II:
-- Interrelationship of Bcrit and Tcrit

101. Applications
OR
Other Features of Superconductors
http://superconductors.org/Uses.htm

102. Meissner Effect

103. Magnetic Levitation – Meissner Effect
Q: Why ?
Kittel states this explusion effect
is not clearly directly connected
to the  = 0 effects

104. Magnetic Levitation – Meissner Effect
MLX01 Test Vehicle
2003 581 km/h 361 mph
2005 80,000+ riders
2005 tested passing trains at relative 1026 km/h
http://www.rtri.or.jp/rd/maglev/html/english/maglev_frame_E.html

105. Maglev in Germany (sc? idi)
32 km track
550,000 km since 1984
Design speed 550 km/h
NOTE(061204): I’m not so sure this track is superconducting. The MagLev planned for the Munich area will be. France is also thinking about a sc maglev.

106. Josephson Junction
~ 2 nm

107. Recall: Aharonov-Bohm Effect
-- from last semester
affects the phase of a wavefunction
Source B

/
)
( 2
~ r
eA
p
i
e 

/
)
( 1
~ r
eA
p
i
e 

/
~
~ ipx
ikx
e
e
A

108. SQUID
superconducting quantum interference device
left
i
oe


 ~
right
i
oe


 ~
o


109. 
i
oe

 ~
)
(location
fn



B
Bohm
Aharonov
loop
q
n
dl


 



 



 
 2
q
n
B



2

2
15
10
07
.
2
)
2
(
2
m
Telsa
e





Add up change in flux as go around loop

110. Typical B fields
(Tesla) (# flux quanta)

111. MAGSAFE will be able to locate
targets without flying close to
the surface.
Image courtesy Department of
Defence.
http://www.csiro.au/science/magsafe.html
Finding 'objects of interest' at sea with MAGSAFE
MAGSAFE is a new system for locating and identifying submarines.
Operators of MAGSAFE should be able to tell the range, depth and
bearing of a target, as well as where it’s heading, how fast it’s going
and if it’s diving.
Building on our extensive experience using highly sensitive magnetic
sensors known as Superconducting QUantum Interference Devices
(SQUIDs) for minerals exploration, MAGSAFE harnesses the power
of three SQUIDs to measure slight variations in the local magnetic
field.
MAGSAFE has higher sensitivity and greater immunity to external noise than conventional
Magnetic Anomaly Detector (MAD) systems. This is especially relevant to operation over shallow
seawater where the background noise may 100 times greater than the noise floor of a MAD
instrument.

112. Phillip Schmidt etal. Exploration Geophysics 35, 297 (2004).
http://www.csiro.au/science/magsafe.html

113. Arian Lalezari

114. SQUID
2 nm
1014 T SQUID threshold
Heart signals 10 10 T
Brain signals 10 13 T

115. • Fundamentals of superconductors:
– http://www.physnet.uni-hamburg.de/home/vms/reimer/htc/pt3.html
• Basic Introduction to SQUIDs:
– http://www.abdn.ac.uk/physics/case/squids.html
• Detection of Submarines
– http://www.csiro.au/science/magsafe.html
• Fancy cross-referenced site for Josephson Junctions/Josephson:
– http://en.wikipedia.org/wiki/Josephson_junction
– http://en.wikipedia.org/wiki/B._D._Josephson
• SQUID sensitivity and other ramifications of Josephson’s work:
– http://hyperphysics.phy-astr.gsu.edu/hbase/solids/squid2.html
• Understanding a SQUID magnetometer:
– http://hyperphysics.phy-astr.gsu.edu/hbase/solids/squid.html#c1
• Some exciting applications of SQUIDs:
– http://www.lanl.gov/quarterly/q_spring03/squid_text.shtml

116. • Relative strengths of pertinent magnetic fields
– http://www.physics.union.edu/newmanj/2000/SQUIDs.htm
• The 1973 Nobel Prize in physics
– http://nobelprize.org/physics/laureates/1973/
• Critical overview of SQUIDs
– http://homepages.nildram.co.uk/~phekda/richdawe/squid/popular/
• Research Applications
– http://boojum.hut.fi/triennial/neuromagnetic.html
• Technical overview of SQUIDs:
– http://www.finoag.com/fitm/squid.html
– http://www.cmp.liv.ac.uk/frink/thesis/thesis/node47.html

117. Redraw LHS
Sn 230 nm
Al 1600
Pb 83
Nb 38
Best conductors  best ‘free-electrons’  no e – lattice interaction
 not superconducting