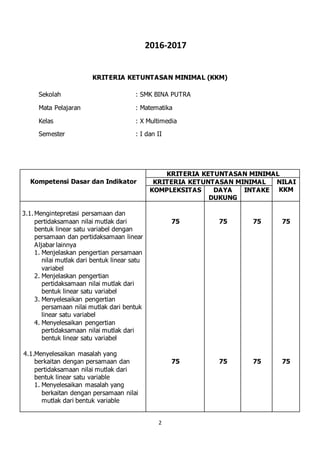
Dokumen tersebut merupakan kriteria ketuntasan minimal (KKM) mata pelajaran matematika untuk kelas X di SMK Bina Putra. Dokumen tersebut menjelaskan KKM untuk berbagai kompetensi dasar matematika seperti aljabar, trigonometri, dan fungsi yang harus dicapai siswa untuk lulus mata pelajaran tersebut.

1. 1
KKM
M A T E M A T I K A
Kelas/Semester : X / 1-2
Nama Guru : Faqih Makhfuddin, S. Pd
Sekolah Menengah Kejuruan
Bina Putra
Jakarta

2. 2
2016-2017
KRITERIA KETUNTASAN MINIMAL (KKM)
Sekolah : SMK BINA PUTRA
Mata Pelajaran : Matematika
Kelas : X Multimedia
Semester : I dan II
Kompetensi Dasar dan Indikator
KRITERIA KETUNTASAN MINIMAL
KRITERIA KETUNTASAN MINIMAL NILAI
KKMKOMPLEKSITAS DAYA
DUKUNG
INTAKE
3.1.Mengintepretasi persamaan dan
pertidaksamaan nilai mutlak dari
bentuk linear satu variabel dengan
persamaan dan pertidaksamaan linear
Aljabar lainnya
1. Menjelaskan pengertian persamaan
nilai mutlak dari bentuk linear satu
variabel
2. Menjelaskan pengertian
pertidaksamaan nilai mutlak dari
bentuk linear satu variabel
3. Menyelesaikan pengertian
persamaan nilai mutlak dari bentuk
linear satu variabel
4. Menyelesaikan pengertian
pertidaksamaan nilai mutlak dari
bentuk linear satu variabel
4.1.Menyelesaikan masalah yang
berkaitan dengan persamaan dan
pertidaksamaan nilai mutlak dari
bentuk linear satu variable
1. Menyelesaikan masalah yang
berkaitan dengan persamaan nilai
mutlak dari bentuk variable
75
75
75
75
75
75
75
75

3. 3
2. Menyelesaikan masalah yang
berkaitan dengan pertidaksamaan
nilai mutlak dari bentuk variable
3.2.Menjelaskan dan menentukan
penyelesaian pertidaksamaan rasional
dan irasional satu variable
1. Menjelaskan pertidaksamaan
rasional satu variable
2. Menentukan langkah – langkah
penyelesaian pertidaksamaan
rasional satu variable
3. Menyelesaikan pertidaksamaan
rasional satu variable
4. Menjelaskan pertidaksamaan
irasional satu variable
5. Menentukan langkah – langkah
penyelesaian pertidaksamaan
irasional satu variable
6. Menyelesaikan pertidaksamaan
irasional satu variable
4.2.Menyelesaikan masalah yang
berkaitan dengan pertidaksamaan
rasional dan irasional satu variable
1. Menyelesaikan masalah kontekstual
yang berkaitan dengan
pertidaksamaan rasional dan
irasional satu variable
3.3.Menyusun sistem persamaan linear
tiga variabel dari masalah kontekstual
1. Menjelaskan konsep system
persamaan linear tiga variable
2. Menyusun system persamaan
linear tiga variabel dari masalah
kontekstual
4.3.Menyelesaikan masalah kontekstual
yang berkaitan dengan sistem
persamaan linear tiga variable
1. Menyelesaikan masalah kontekstual
yang berkaitan dengan system
persamaan linear tiga variable
3.4.Menjelaskan dan menentukan
penyelesaian system pertidaksamaan
dua variabel (linier kuadrat dan
kuadrat – kuadrat)
1. Menjelaskan dan menentukan
penyelesaian sistem
75
75
75
75
75
75
75
75
75
75
75
75
75
75
75
75
75
75
75
75

4. 4
pertidaksamaan dua variabel dalam
bentuk linier – kuadrat
2. Menjelaskan dan Menentukan
penyelesaian sistem
pertidaksamaan dua variabel dalam
bentuk kuadrat–kuadrat
4.4.Menyajikan dan menyelesaikan
masalah yang berkaitan dengan
system pertidaksaman dua variabel
(linier – kuadrat dan kuadrat –
kuadrat)
1. Menyusun system pertidaksaman
dua variabel dalam bentuk linier–
kuadrat dan kuadrat – kuadrat
2. Menyelesaikan masalah yang
berkaitan dengan system
pertidaksaman dua variabel dalam
bentuk linier–kuadrat dan
kuadrat–kuadrat
3.5. Menjelaskan dan menentukan fungsi
(terutama fungsi linear, fungsi
kuadrat, dan fungsi rasional) secara
formal yang meliputi notasi, daerah
asal, daerah hasil, dan ekspresi
simbolik, serta sketsa grafiknya.
1. Menjelaskan dan menentukan
fungsi linier secara formal yang
meliputi notasi, daerah asal,
daerah hasil, dan ekspresi
simbolik, serta sketsa grafiknya.
2. Menjelaskan dan menentukan
fungsi kuadrat secara formal yang
meliputi notasi, daerah asal,
daerah hasil, dan ekspresi
simbolik, serta sketsa grafiknya.
3. Menjelaskan dan menentukan
fungsi rasional secara formal yang
meliputi notasi, daerah asal,
daerah hasil, dan ekspresi
simbolik, serta sketsa grafiknya
4.5. Menganalisa karakteristik masing –
masing grafik (titik potong dengan
sumbu, titik puncak, asimtot) dan
perubahan grafik fungsinya akibat
transformasi f2(x), 1/f(x), |f(x)| dsb
1. Menganalisa karakteristik grafik
titik potong dengan sumbu pada
fungsi linear dan kuadrat
75
75
75
75
75
75
75
75
75
75
75
75

5. 5
2. Menganalisa karakteristik grafik
titik puncak dan asimtot pada
fungsi kuadrat
3. Menganalisa perubahan grafik
fungsinya akibat transformasi
f2(x), 1/f(x), |f(x)|
3.6. Menjelaskan operasi komposisi
fungsi dan operasi fungsi invers serta
sifat-sifatnya serta menentukan
eksistensinya
1. Menjelaskan konsep dan operasi
komposisi fungsi berdasarkan
sifat-sifatnya
2. Mejelaskan konsep dan operasi
invers berdasarkan sifat-sifatnya
4.6. Menyelesaikan masalah yang
berkaitan dengan operasi komposisi
dan operasi invers suatu fungsi
1. Menyelesaikan masalah
kontekstual yang berkaitan
dengan operasi fungsi komposisi
2. Menyelesaikan masalah
kontekstual yang berkaitan
dengan operasi fungsi invers
3.7. Menjelaskan rasio trigonometri
(sinus, cosinus, tangen, cosecan,
secan, dan cotangen) pada segitiga
siku-siku
1. Menjelaskan dan menentukan
rasio trigonometri (sinus, cosinus,
tangen) pada segitiga siku siku
2. Menjelaskan dan menentukan
rasio trigonometri (cosecan,
secan, cotangen) pada segitiga
siku siku
4.7. Menyelesaikan masalah kontekstual
yang berkaitan dengan rasio
trigonometri (sinus, cosinus, tangen,
cosecan, secan, dan cotangen) pada
segitiga siku-siku
1. Menyelesaikan masalah
kontekstual yang berkaitan
dengan rasio trigonometri (sinus,
cosinus, tangen) pada segitiga
siku siku
2. Menyelesaikan masalah
kontekstual yang berkaitan
dengan rasio trigonometri
75
75
75
75
75
75
75
75
75
75
75
75
75
75
75
75

6. 6
(cosecan, secan dan contangen)
pada segitiga siku siku
3.8. Menggeneralisasi rasio trigonometri
untuk sudut-sudut di berbagai
kuadran dan sudut-sudut berelasi
1. Menjelaskan hubungan rasio
trigonometri untuk sudut-sudut di
berbagai kuadran dan sudut-
sudut berelasi
2. Menerapkan rasio trigonometri
untuk sudut-sudut di berbagai
kuadran dan sudut-sudut berelasi
3. Menyimpulkan rasio trigonometri
untuk sudut-sudut di berbagai
kuadran dan sudut-sudut berelasi
4.8. Menyelesaikan masalah kontekstual
yang berkaitan dengan rasio
trigonometri sudut-sudut di berbagai
kuadran dan sudut-sudut berelasi
1. Menyelesaikan masalah
kontekstual yang berkaitan
dengan rasio trigonometri sudut-
sudut di berbagai kuadran dan
sudut-sudut berelasi
3.9. Menjelaskan identitas dasar
trigonometri sebagai hubungan
antara rasio trigonometri dan
perannya dalam membuktikan
identitas trigonometri lainnya.
1. Menemukan sifat-sifat dan
hubungan antar perbandingan
trigonometri dalam segitiga siku-
Siku dan identitas trigonometri
4.9. Menggunakan identitas dasar
trigonometri untuk membuktikan
identitas trigonometri lainnya.
Mendemonstrasikan konsep fungsi
trigonometri berdasarkan tugas.
1. Mendemonstrasikan konsep fungsi
trigonometri berdasarkan tugas.
3.10. Menjelaskan dan menentukan
fungsi trigonometri dengan
menggunakan lingkaran satuan
1. Menjelaskan konsep fungsi
trigonometri berdasarkan bentuk
dan nilai fungsi
75
75
75
75
75
75
75
75
75
75
75
75
75
75
75
75
75
75
75
75

7. 7
2. Menentukan nilai fungsi
trigometri dengan menggunakan
lingkaran satuan
4.10. Menganalisa perubahan grafik
fungsi trigonometri akibat
perubahan pada konstanta pada
fungsi y = a sin b (x+c) + d
1. Menganalisa perubahan grafik
fungsi akibat perubahan pada
kostanta “a,b, c dan d” pada
fungsi y = a sin b (x+c) + d
75 75 75 75
Mengetahui, Jakarta, 18 Agustus 2016
Kepala SMK Bina Putra Guru Mata Pelajaran
H. Muhammad, S. Pd Faqih Makhfuddin, S. Pd