Ap2 unit5 open stax notes

22 MAGNETISM
Figure 22.1 The magnificent spectacle of the Aurora Borealis, or northern lights, glows in the northern sky above Bear Lake near Eielson Air Force
Base, Alaska. Shaped by the Earth’s magnetic field, this light is produced by radiation spewed from solar storms. (credit: Senior Airman Joshua Strang,
via Flickr)
Chapter Outline
22.1. Magnets
22.2. Ferromagnets and Electromagnets
22.3. Magnetic Fields and Magnetic Field Lines
22.4. Magnetic Field Strength: Force on a Moving Charge in a Magnetic Field
22.5. Force on a Moving Charge in a Magnetic Field: Examples and Applications
22.6. The Hall Effect
22.7. Magnetic Force on a Current-Carrying Conductor
22.8. Torque on a Current Loop: Motors and Meters
22.9. Magnetic Fields Produced by Currents: Ampere’s Law
22.10. Magnetic Force between Two Parallel Conductors
22.11. More Applications of Magnetism
Connection for AP® Courses
Magnetism plays a major role in your everyday life. All electric motors, with uses as diverse as powering refrigerators, starting
cars, and moving elevators, contain magnets. Magnetic resonance imaging (MRI) has become an important diagnostic tool in the
field of medicine, and the use of magnetism to explore brain activity is a subject of contemporary research and development.
Other applications of magnetism include computer memory, levitation of high-speed trains, the aurora borealis, and, of course,
the first important historical use of magnetism: navigation. You will find all of these applications of magnetism linked by a small
number of underlying principles.
In this chapter, you will learn that both the internal properties of an object and the movement of charged particles can generate a
magnetic field, and you will learn why all magnetic fields have a north and south pole. You will also learn how magnetic fields
exert forces on objects, resulting in the magnetic alignment that makes a compass work. You will learn how we use this principle
to weigh the smallest of subatomic particles with precision and contain superheated plasma to facilitate nuclear fusion.
Big Idea 1 Objects and systems have properties such as mass and charge. Systems may have internal structure.
Enduring Understanding 1.E Materials have many macroscopic properties that result from the arrangement and interactions of
the atoms and molecules that make up the material.
Essential Knowledge 1.E.5 Matter has a property called magnetic permeability.
Chapter 22 | Magnetism 965

Essential Knowledge 1.E.6 Matter has a property called magnetic dipole moment.
Big Idea 2 Fields existing in space can be used to explain interactions.
Enduring Understanding 2.D A magnetic field is caused by a magnet or a moving electrically charged object. Magnetic fields
observed in nature always seem to be produced either by moving charged objects or by magnetic dipoles or combinations of
dipoles and never by single poles.
Essential Knowledge 2.D.1 The magnetic field exerts a force on a moving electrically charged object. That magnetic force is
perpendicular to the direction of the velocity of the object and to the magnetic field and is proportional to the magnitude of the
charge, the magnitude of the velocity, and the magnitude of the magnetic field. It also depends on the angle between the velocity
and the magnetic field vectors. Treatment is quantitative for angles of 0°, 90°, or 180° and qualitative for other angles.
Essential Knowledge 2.D.2 The magnetic field vectors around a straight wire that carries electric current are tangent to
concentric circles centered on that wire. The field has no component toward the current-carrying wire.
Essential Knowledge 2.D.3 A magnetic dipole placed in a magnetic field, such as the ones created by a magnet or the Earth, will
tend to align with the magnetic field vector.
Essential Knowledge 2.D.4 Ferromagnetic materials contain magnetic domains that are themselves magnets.
Big Idea 3 The interactions of an object with other objects can be described by forces.
Enduring Understanding 3.C At the macroscopic level, forces can be categorized as either long-range (action-at-a-distance)
forces or contact forces.
Essential Knowledge 3.C.3 A magnetic force results from the interaction of a moving charged object or a magnet with other
moving charged objects or another magnet.
Big Idea 4 Interactions between systems can result in changes in those systems.
Enduring Understanding 4.E The electric and magnetic properties of a system can change in response to the presence of, or
changes in, other objects or systems.
Essential Knowledge 4.E.1 The magnetic properties of some materials can be affected by magnetic fields at the system.
Students should focus on the underlying concepts and not the use of the vocabulary.
Figure 22.2 Engineering of technology like iPods would not be possible without a deep understanding of magnetism. (credit: Jesse! S?, Flickr)
22.1 Magnets
Learning Objectives
By the end of this section, you will be able to:
• Describe the difference between the north and south poles of a magnet.
• Describe how magnetic poles interact with each other.
966 Chapter 22 | Magnetism
This content is available for free at http://cnx.org/content/col11844/1.13

Figure 22.3 Magnets come in various shapes, sizes, and strengths. All have both a north pole and a south pole. There is never an isolated pole (a
monopole).
All magnets attract iron, such as that in a refrigerator door. However, magnets may attract or repel other magnets.
Experimentation shows that all magnets have two poles. If freely suspended, one pole will point toward the north. The two poles
are thus named the north magnetic pole and the south magnetic pole (or more properly, north-seeking and south-seeking
poles, for the attractions in those directions).
Universal Characteristics of Magnets and Magnetic Poles
It is a universal characteristic of all magnets that like poles repel and unlike poles attract. (Note the similarity with
electrostatics: unlike charges attract and like charges repel.)
Further experimentation shows that it is impossible to separate north and south poles in the manner that + and − charges
can be separated.
Figure 22.4 One end of a bar magnet is suspended from a thread that points toward north. The magnet’s two poles are labeled N and S for north-
seeking and south-seeking poles, respectively.
Misconception Alert: Earth’s Geographic North Pole Hides an S
The Earth acts like a very large bar magnet with its south-seeking pole near the geographic North Pole. That is why the
north pole of your compass is attracted toward the geographic north pole of the Earth—because the magnetic pole that is
near the geographic North Pole is actually a south magnetic pole! Confusion arises because the geographic term “North
Pole” has come to be used (incorrectly) for the magnetic pole that is near the North Pole. Thus, “North magnetic pole” is
actually a misnomer—it should be called the South magnetic pole.

Figure 22.5 Unlike poles attract, whereas like poles repel.
Figure 22.6 North and south poles always occur in pairs. Attempts to separate them result in more pairs of poles. If we continue to split the magnet, we
will eventually get down to an iron atom with a north pole and a south pole—these, too, cannot be separated.
Real World Connections: Dipoles and Monopoles
Figure 22.6 shows that no matter how many times you divide a magnet the resulting objects are always magnetic dipoles.
Formally, a magnetic dipole is an object (usually very small) with a north and south magnetic pole. Magnetic dipoles have a
vector property called magnetic momentum. The magnitude of this vector is equal to the strength of its poles and the
distance between the poles, and the direction points from the south pole to the north pole.
A magnetic dipole can also be thought of as a very small closed current loop. There is no way to isolate north and south
magnetic poles like you can isolate positive and negative charges. Another way of saying this is that magnetic fields of a
magnetic object always make closed loops, starting at a north pole and ending at a south pole.
With a positive charge, you might imagine drawing a spherical surface enclosing that charge, and there would be a net flux
of electric field lines flowing outward through that surface. In fact, Gauss’s law states that the electric flux through a surface
is proportional to the amount of charge enclosed.
With a magnetic object, every surface you can imagine that encloses all or part of the magnet ultimately has zero net flux of
magnetic field lines flowing through the surface. Just as many outward-flowing lines from the north pole of the magnet pass
through the surface as inward-flowing lines from the south pole of the magnet.
Some physicists have theorized that magnetic monopoles exist. These would be isolated magnetic “charges” that would only
generate field lines that flow outward or inward (not loops). Despite many searches, we have yet to experimentally verify the
existence of magnetic monopoles.

The fact that magnetic poles always occur in pairs of north and south is true from the very large scale—for example, sunspots
always occur in pairs that are north and south magnetic poles—all the way down to the very small scale. Magnetic atoms have
both a north pole and a south pole, as do many types of subatomic particles, such as electrons, protons, and neutrons.
Making Connections: Take-Home Experiment—Refrigerator Magnets
We know that like magnetic poles repel and unlike poles attract. See if you can show this for two refrigerator magnets. Will
the magnets stick if you turn them over? Why do they stick to the door anyway? What can you say about the magnetic
properties of the door next to the magnet? Do refrigerator magnets stick to metal or plastic spoons? Do they stick to all types
of metal?
22.2 Ferromagnets and Electromagnets
Learning Objectives
• Define ferromagnet.
• Describe the role of magnetic domains in magnetization.
• Explain the significance of the Curie temperature.
• Describe the relationship between electricity and magnetism.
The information presented in this section supports the following AP® learning objectives and science practices:
• 2.D.3.1 The student is able to describe the orientation of a magnetic dipole placed in a magnetic field in general and the
particular cases of a compass in the magnetic field of the Earth and iron filings surrounding a bar magnet. (S.P. 1.2)
• 2.D.4.1 The student is able to use the representation of magnetic domains to qualitatively analyze the magnetic
behavior of a bar magnet composed of ferromagnetic material. (S.P. 1.4)
• 4.E.1.1 The student is able to use representations and models to qualitatively describe the magnetic properties of some
materials that can be affected by magnetic properties of other objects in the system. (S.P. 1.1, 1.4, 2.2)
Ferromagnets
Only certain materials, such as iron, cobalt, nickel, and gadolinium, exhibit strong magnetic effects. Such materials are called
ferromagnetic, after the Latin word for iron, ferrum. A group of materials made from the alloys of the rare earth elements are
also used as strong and permanent magnets; a popular one is neodymium. Other materials exhibit weak magnetic effects, which
are detectable only with sensitive instruments. Not only do ferromagnetic materials respond strongly to magnets (the way iron is
attracted to magnets), they can also be magnetized themselves—that is, they can be induced to be magnetic or made into
permanent magnets.
Figure 22.7 An unmagnetized piece of iron is placed between two magnets, heated, and then cooled, or simply tapped when cold. The iron becomes a
permanent magnet with the poles aligned as shown: its south pole is adjacent to the north pole of the original magnet, and its north pole is adjacent to
the south pole of the original magnet. Note that there are attractive forces between the magnets.
When a magnet is brought near a previously unmagnetized ferromagnetic material, it causes local magnetization of the material
with unlike poles closest, as in Figure 22.7. (This results in the attraction of the previously unmagnetized material to the magnet.)
What happens on a microscopic scale is illustrated in Figure 22.8. The regions within the material called domains act like small
bar magnets. Within domains, the poles of individual atoms are aligned. Each atom acts like a tiny bar magnet. Domains are
small and randomly oriented in an unmagnetized ferromagnetic object. In response to an external magnetic field, the domains
may grow to millimeter size, aligning themselves as shown in Figure 22.8(b). This induced magnetization can be made
permanent if the material is heated and then cooled, or simply tapped in the presence of other magnets.

Figure 22.8 (a) An unmagnetized piece of iron (or other ferromagnetic material) has randomly oriented domains. (b) When magnetized by an external
field, the domains show greater alignment, and some grow at the expense of others. Individual atoms are aligned within domains; each atom acts like a
tiny bar magnet.
Conversely, a permanent magnet can be demagnetized by hard blows or by heating it in the absence of another magnet.
Increased thermal motion at higher temperature can disrupt and randomize the orientation and the size of the domains. There is
a well-defined temperature for ferromagnetic materials, which is called the Curie temperature, above which they cannot be
magnetized. The Curie temperature for iron is 1043 K (770ºC) , which is well above room temperature. There are several
elements and alloys that have Curie temperatures much lower than room temperature and are ferromagnetic only below those
temperatures.
Electromagnets
Early in the 19th century, it was discovered that electrical currents cause magnetic effects. The first significant observation was
by the Danish scientist Hans Christian Oersted (1777–1851), who found that a compass needle was deflected by a current-
carrying wire. This was the first significant evidence that the movement of charges had any connection with magnets.
Electromagnetism is the use of electric current to make magnets. These temporarily induced magnets are called
electromagnets. Electromagnets are employed for everything from a wrecking yard crane that lifts scrapped cars to controlling
the beam of a 90-km-circumference particle accelerator to the magnets in medical imaging machines (See Figure 22.9).
Figure 22.9 Instrument for magnetic resonance imaging (MRI). The device uses a superconducting cylindrical coil for the main magnetic field. The
patient goes into this “tunnel” on the gurney. (credit: Bill McChesney, Flickr)
Figure 22.10 shows that the response of iron filings to a current-carrying coil and to a permanent bar magnet. The patterns are
similar. In fact, electromagnets and ferromagnets have the same basic characteristics—for example, they have north and south
poles that cannot be separated and for which like poles repel and unlike poles attract.

Figure 22.10 Iron filings near (a) a current-carrying coil and (b) a magnet act like tiny compass needles, showing the shape of their fields. Their
response to a current-carrying coil and a permanent magnet is seen to be very similar, especially near the ends of the coil and the magnet.
Making Connections: Compasses
Figure 22.11 Compass needles and a bar magnet.
In Figure 22.11, a series of tiny compass needles are placed in an external magnetic field. These dipoles respond exactly
like the iron filings in Figure 22.10. For needles close to one pole of the magnet, the needle is aligned so that the opposite
pole of the needle points at the bar magnet. For example, close to the north pole of the bar magnet, the south pole of the
compass needle is aligned to be closest to the bar magnet.
As an experimenter moves each compass around, the needle will rotate in such a way as to orient itself with the field of the
bar magnet at that location. In this way, the magnetic field lines may be mapped out precisely.
The strength of the magnetic field depends on the medium in which the magnetic field exists. Some substances (like iron)
respond to external magnetic fields in a way that amplifies the external magnetic field. The magnetic permeability of a
substance is a measure of the substance’s ability to support or amplify an already existing external magnetic field.
Ferromagnets, in which magnetic domains in the substance align with and amplify an external magnetic field, are examples
of objects with high permeability.
Combining a ferromagnet with an electromagnet can produce particularly strong magnetic effects. (See Figure 22.12.) Whenever
strong magnetic effects are needed, such as lifting scrap metal, or in particle accelerators, electromagnets are enhanced by
ferromagnetic materials. Limits to how strong the magnets can be made are imposed by coil resistance (it will overheat and melt
at sufficiently high current), and so superconducting magnets may be employed. These are still limited, because superconducting
properties are destroyed by too great a magnetic field.

Figure 22.12 An electromagnet with a ferromagnetic core can produce very strong magnetic effects. Alignment of domains in the core produces a
magnet, the poles of which are aligned with the electromagnet.
Figure 22.13 shows a few uses of combinations of electromagnets and ferromagnets. Ferromagnetic materials can act as
memory devices, because the orientation of the magnetic fields of small domains can be reversed or erased. Magnetic
information storage on videotapes and computer hard drives are among the most common applications. This property is vital in
our digital world.
Figure 22.13 An electromagnet induces regions of permanent magnetism on a floppy disk coated with a ferromagnetic material. The information stored
here is digital (a region is either magnetic or not); in other applications, it can be analog (with a varying strength), such as on audiotapes.
Current: The Source of All Magnetism
An electromagnet creates magnetism with an electric current. In later sections we explore this more quantitatively, finding the
strength and direction of magnetic fields created by various currents. But what about ferromagnets? Figure 22.14 shows models
of how electric currents create magnetism at the submicroscopic level. (Note that we cannot directly observe the paths of
individual electrons about atoms, and so a model or visual image, consistent with all direct observations, is made. We can
directly observe the electron’s orbital angular momentum, its spin momentum, and subsequent magnetic moments, all of which
are explained with electric-current-creating subatomic magnetism.) Currents, including those associated with other
submicroscopic particles like protons, allow us to explain ferromagnetism and all other magnetic effects. Ferromagnetism, for
example, results from an internal cooperative alignment of electron spins, possible in some materials but not in others.
Crucial to the statement that electric current is the source of all magnetism is the fact that it is impossible to separate north and
south magnetic poles. (This is far different from the case of positive and negative charges, which are easily separated.) A current
loop always produces a magnetic dipole—that is, a magnetic field that acts like a north pole and south pole pair. Since isolated
north and south magnetic poles, called magnetic monopoles, are not observed, currents are used to explain all magnetic
effects. If magnetic monopoles did exist, then we would have to modify this underlying connection that all magnetism is due to
electrical current. There is no known reason that magnetic monopoles should not exist—they are simply never observed—and so

searches at the subnuclear level continue. If they do not exist, we would like to find out why not. If they do exist, we would like to
see evidence of them.
Electric Currents and Magnetism
Electric current is the source of all magnetism.
Figure 22.14 (a) In the planetary model of the atom, an electron orbits a nucleus, forming a closed-current loop and producing a magnetic field with a
north pole and a south pole. (b) Electrons have spin and can be crudely pictured as rotating charge, forming a current that produces a magnetic field
with a north pole and a south pole. Neither the planetary model nor the image of a spinning electron is completely consistent with modern physics.
However, they do provide a useful way of understanding phenomena.
PhET Explorations: Magnets and Electromagnets
Explore the interactions between a compass and bar magnet. Discover how you can use a battery and wire to make a
magnet! Can you make it a stronger magnet? Can you make the magnetic field reverse?
Figure 22.15 Magnets and Electromagnets (http://cnx.org/content/m55375/1.2/magnets-and-electromagnets_en.jar)
22.3 Magnetic Fields and Magnetic Field Lines
Learning Objectives
• Define magnetic field and describe the magnetic field lines of various magnetic fields.
Einstein is said to have been fascinated by a compass as a child, perhaps musing on how the needle felt a force without direct
physical contact. His ability to think deeply and clearly about action at a distance, particularly for gravitational, electric, and
magnetic forces, later enabled him to create his revolutionary theory of relativity. Since magnetic forces act at a distance, we
define a magnetic field to represent magnetic forces. The pictorial representation of magnetic field lines is very useful in
visualizing the strength and direction of the magnetic field. As shown in Figure 22.16, the direction of magnetic field lines is
defined to be the direction in which the north end of a compass needle points. The magnetic field is traditionally called the B-
field.

Figure 22.16 Magnetic field lines are defined to have the direction that a small compass points when placed at a location. (a) If small compasses are
used to map the magnetic field around a bar magnet, they will point in the directions shown: away from the north pole of the magnet, toward the south
pole of the magnet. (Recall that the Earth’s north magnetic pole is really a south pole in terms of definitions of poles on a bar magnet.) (b) Connecting
the arrows gives continuous magnetic field lines. The strength of the field is proportional to the closeness (or density) of the lines. (c) If the interior of
the magnet could be probed, the field lines would be found to form continuous closed loops.
Small compasses used to test a magnetic field will not disturb it. (This is analogous to the way we tested electric fields with a
small test charge. In both cases, the fields represent only the object creating them and not the probe testing them.) Figure 22.17
shows how the magnetic field appears for a current loop and a long straight wire, as could be explored with small compasses. A
small compass placed in these fields will align itself parallel to the field line at its location, with its north pole pointing in the
direction of B. Note the symbols used for field into and out of the paper.
Figure 22.17 Small compasses could be used to map the fields shown here. (a) The magnetic field of a circular current loop is similar to that of a bar
magnet. (b) A long and straight wire creates a field with magnetic field lines forming circular loops. (c) When the wire is in the plane of the paper, the
field is perpendicular to the paper. Note that the symbols used for the field pointing inward (like the tail of an arrow) and the field pointing outward (like
the tip of an arrow).
Making Connections: Concept of a Field
A field is a way of mapping forces surrounding any object that can act on another object at a distance without apparent
physical connection. The field represents the object generating it. Gravitational fields map gravitational forces, electric fields
map electrical forces, and magnetic fields map magnetic forces.
Extensive exploration of magnetic fields has revealed a number of hard-and-fast rules. We use magnetic field lines to represent
the field (the lines are a pictorial tool, not a physical entity in and of themselves). The properties of magnetic field lines can be
summarized by these rules:
1. The direction of the magnetic field is tangent to the field line at any point in space. A small compass will point in the
direction of the field line.
2. The strength of the field is proportional to the closeness of the lines. It is exactly proportional to the number of lines per unit
area perpendicular to the lines (called the areal density).
3. Magnetic field lines can never cross, meaning that the field is unique at any point in space.
4. Magnetic field lines are continuous, forming closed loops without beginning or end. They go from the north pole to the south
pole.
The last property is related to the fact that the north and south poles cannot be separated. It is a distinct difference from electric
field lines, which begin and end on the positive and negative charges. If magnetic monopoles existed, then magnetic field lines
would begin and end on them.

22.4 Magnetic Field Strength: Force on a Moving Charge in a Magnetic Field
Learning Objectives
• Describe the effects of magnetic fields on moving charges.
• Use the right-hand rule 1 to determine the velocity of a charge, the direction of the magnetic field, and the direction of
magnetic force on a moving charge.
• Calculate the magnetic force on a moving charge.
• 2.D.1.1 The student is able to apply mathematical routines to express the force exerted on a moving charged object by
a magnetic field. (S.P. 2.2)
• 3.C.3.1 The student is able to use right-hand rules to analyze a situation involving a current-carrying conductor and a
moving electrically charged object to determine the direction of the magnetic force exerted on the charged object due to
the magnetic field created by the current-carrying conductor. (S.P. 1.4)
What is the mechanism by which one magnet exerts a force on another? The answer is related to the fact that all magnetism is
caused by current, the flow of charge. Magnetic fields exert forces on moving charges, and so they exert forces on other
magnets, all of which have moving charges.
Right Hand Rule 1
The magnetic force on a moving charge is one of the most fundamental known. Magnetic force is as important as the
electrostatic or Coulomb force. Yet the magnetic force is more complex, in both the number of factors that affects it and in its
direction, than the relatively simple Coulomb force. The magnitude of the magnetic force F on a charge q moving at a speed
v in a magnetic field of strength B is given by
(22.1)F = qvB sin θ,
where θ is the angle between the directions of v and B. This force is often called the Lorentz force. In fact, this is how we
define the magnetic field strength B —in terms of the force on a charged particle moving in a magnetic field. The SI unit for
magnetic field strength B is called the tesla (T) after the eccentric but brilliant inventor Nikola Tesla (1856–1943). To determine
how the tesla relates to other SI units, we solve F = qvB sin θ for B .
(22.2)
B = F
qv sin θ
Because sin θ is unitless, the tesla is
(22.3)
1 T = 1 N
C ⋅ m/s
= 1 N
A ⋅ m
(note that C/s = A).
Another smaller unit, called the gauss (G), where 1 G = 10−4
T , is sometimes used. The strongest permanent magnets have
fields near 2 T; superconducting electromagnets may attain 10 T or more. The Earth’s magnetic field on its surface is only about
5×10−5
T , or 0.5 G.
The direction of the magnetic force F is perpendicular to the plane formed by v and B , as determined by the right hand rule
1 (or RHR-1), which is illustrated in Figure 22.18. RHR-1 states that, to determine the direction of the magnetic force on a
positive moving charge, you point the thumb of the right hand in the direction of v , the fingers in the direction of B , and a
perpendicular to the palm points in the direction of F . One way to remember this is that there is one velocity, and so the thumb
represents it. There are many field lines, and so the fingers represent them. The force is in the direction you would push with
your palm. The force on a negative charge is in exactly the opposite direction to that on a positive charge.

Figure 22.18 Magnetic fields exert forces on moving charges. This force is one of the most basic known. The direction of the magnetic force on a
moving charge is perpendicular to the plane formed by v and B and follows right hand rule–1 (RHR-1) as shown. The magnitude of the force is
proportional to q , v , B , and the sine of the angle between v and B .
Making Connections: Charges and Magnets
There is no magnetic force on static charges. However, there is a magnetic force on moving charges. When charges are
stationary, their electric fields do not affect magnets. But, when charges move, they produce magnetic fields that exert forces
on other magnets. When there is relative motion, a connection between electric and magnetic fields emerges—each affects
the other.
Example 22.1 Calculating Magnetic Force: Earth’s Magnetic Field on a Charged Glass Rod
With the exception of compasses, you seldom see or personally experience forces due to the Earth’s small magnetic field.
To illustrate this, suppose that in a physics lab you rub a glass rod with silk, placing a 20-nC positive charge on it. Calculate
the force on the rod due to the Earth’s magnetic field, if you throw it with a horizontal velocity of 10 m/s due west in a place
where the Earth’s field is due north parallel to the ground. (The direction of the force is determined with right hand rule 1 as
shown in Figure 22.19.)
Figure 22.19 A positively charged object moving due west in a region where the Earth’s magnetic field is due north experiences a force that is
straight down as shown. A negative charge moving in the same direction would feel a force straight up.
Strategy

We are given the charge, its velocity, and the magnetic field strength and direction. We can thus use the equation
F = qvB sin θ to find the force.
Solution
The magnetic force is
(22.4)F = qvb sin θ.
We see that sin θ = 1 , since the angle between the velocity and the direction of the field is 90º . Entering the other given
quantities yields
(22.5)F = ⎛
⎝20×10–9
C⎞
⎠(10 m/s)⎛
⎝5×10–5
T⎞
⎠
= 1×10–11
(C ⋅ m/s)
⎛
⎝
N
C ⋅ m/s
⎞
⎠ = 1×10–11
N.
Discussion
This force is completely negligible on any macroscopic object, consistent with experience. (It is calculated to only one digit,
since the Earth’s field varies with location and is given to only one digit.) The Earth’s magnetic field, however, does produce
very important effects, particularly on submicroscopic particles. Some of these are explored in Force on a Moving Charge
in a Magnetic Field: Examples and Applications.
22.5 Force on a Moving Charge in a Magnetic Field: Examples and Applications
Learning Objectives
• Describe the effects of a magnetic field on a moving charge.
• Calculate the radius of curvature of the path of a charge that is moving in a magnetic field.
Magnetic force can cause a charged particle to move in a circular or spiral path. Cosmic rays are energetic charged particles in
outer space, some of which approach the Earth. They can be forced into spiral paths by the Earth’s magnetic field. Protons in
giant accelerators are kept in a circular path by magnetic force. The bubble chamber photograph in Figure 22.20 shows charged
particles moving in such curved paths. The curved paths of charged particles in magnetic fields are the basis of a number of
phenomena and can even be used analytically, such as in a mass spectrometer.
Figure 22.20 Trails of bubbles are produced by high-energy charged particles moving through the superheated liquid hydrogen in this artist’s rendition
of a bubble chamber. There is a strong magnetic field perpendicular to the page that causes the curved paths of the particles. The radius of the path
can be used to find the mass, charge, and energy of the particle.
So does the magnetic force cause circular motion? Magnetic force is always perpendicular to velocity, so that it does no work on
the charged particle. The particle’s kinetic energy and speed thus remain constant. The direction of motion is affected, but not the
speed. This is typical of uniform circular motion. The simplest case occurs when a charged particle moves perpendicular to a

uniform B -field, such as shown in Figure 22.21. (If this takes place in a vacuum, the magnetic field is the dominant factor
determining the motion.) Here, the magnetic force supplies the centripetal force Fc = mv2
/ r . Noting that sin θ = 1 , we see
that F = qvB .
Figure 22.21 A negatively charged particle moves in the plane of the page in a region where the magnetic field is perpendicular into the page
(represented by the small circles with x’s—like the tails of arrows). The magnetic force is perpendicular to the velocity, and so velocity changes in
direction but not magnitude. Uniform circular motion results.
Because the magnetic force F supplies the centripetal force Fc , we have
(22.6)
qvB = mv2
r .
Solving for r yields
(22.7)r = mv
qB
.
Here, r is the radius of curvature of the path of a charged particle with mass m and charge q , moving at a speed v
perpendicular to a magnetic field of strength B . If the velocity is not perpendicular to the magnetic field, then v is the
component of the velocity perpendicular to the field. The component of the velocity parallel to the field is unaffected, since the
magnetic force is zero for motion parallel to the field. This produces a spiral motion rather than a circular one.
Example 22.2 Calculating the Curvature of the Path of an Electron Moving in a Magnetic Field: A
Magnet on a TV Screen
A magnet brought near an old-fashioned TV screen such as in Figure 22.22 (TV sets with cathode ray tubes instead of LCD
screens) severely distorts its picture by altering the path of the electrons that make its phosphors glow. (Don’t try this at
home, as it will permanently magnetize and ruin the TV.) To illustrate this, calculate the radius of curvature of the path of
an electron having a velocity of 6.00×107
m/s (corresponding to the accelerating voltage of about 10.0 kV used in some
TVs) perpendicular to a magnetic field of strength B = 0.500 T (obtainable with permanent magnets).

Figure 22.22 Side view showing what happens when a magnet comes in contact with a computer monitor or TV screen. Electrons moving toward
the screen spiral about magnetic field lines, maintaining the component of their velocity parallel to the field lines. This distorts the image on the
screen.
Strategy
We can find the radius of curvature r directly from the equation r = mv
qB
, since all other quantities in it are given or known.
Solution
Using known values for the mass and charge of an electron, along with the given values of v and B gives us
(22.8)
r = mv
qB
=
⎛
⎝9.11×10−31
kg⎞
⎠
⎛
⎝6.00×107
m/s⎞
⎠
⎛
⎝1.60×10−19
C⎞
⎠(0.500 T)
= 6.83×10−4
m
or
(22.9)r = 0.683 mm.
Discussion
The small radius indicates a large effect. The electrons in the TV picture tube are made to move in very tight circles, greatly
altering their paths and distorting the image.
Figure 22.23 shows how electrons not moving perpendicular to magnetic field lines follow the field lines. The component of
velocity parallel to the lines is unaffected, and so the charges spiral along the field lines. If field strength increases in the direction
of motion, the field will exert a force to slow the charges, forming a kind of magnetic mirror, as shown below.
Figure 22.23 When a charged particle moves along a magnetic field line into a region where the field becomes stronger, the particle experiences a
force that reduces the component of velocity parallel to the field. This force slows the motion along the field line and here reverses it, forming a
“magnetic mirror.”
The properties of charged particles in magnetic fields are related to such different things as the Aurora Australis or Aurora
Borealis and particle accelerators. Charged particles approaching magnetic field lines may get trapped in spiral orbits about the
lines rather than crossing them, as seen above. Some cosmic rays, for example, follow the Earth’s magnetic field lines, entering
the atmosphere near the magnetic poles and causing the southern or northern lights through their ionization of molecules in the

atmosphere. This glow of energized atoms and molecules is seen in Figure 22.1. Those particles that approach middle latitudes
must cross magnetic field lines, and many are prevented from penetrating the atmosphere. Cosmic rays are a component of
background radiation; consequently, they give a higher radiation dose at the poles than at the equator.
Figure 22.24 Energetic electrons and protons, components of cosmic rays, from the Sun and deep outer space often follow the Earth’s magnetic field
lines rather than cross them. (Recall that the Earth’s north magnetic pole is really a south pole in terms of a bar magnet.)
Some incoming charged particles become trapped in the Earth’s magnetic field, forming two belts above the atmosphere known
as the Van Allen radiation belts after the discoverer James A. Van Allen, an American astrophysicist. (See Figure 22.25.)
Particles trapped in these belts form radiation fields (similar to nuclear radiation) so intense that manned space flights avoid them
and satellites with sensitive electronics are kept out of them. In the few minutes it took lunar missions to cross the Van Allen
radiation belts, astronauts received radiation doses more than twice the allowed annual exposure for radiation workers. Other
planets have similar belts, especially those having strong magnetic fields like Jupiter.
Figure 22.25 The Van Allen radiation belts are two regions in which energetic charged particles are trapped in the Earth’s magnetic field. One belt lies
about 300 km above the Earth’s surface, the other about 16,000 km. Charged particles in these belts migrate along magnetic field lines and are
partially reflected away from the poles by the stronger fields there. The charged particles that enter the atmosphere are replenished by the Sun and
sources in deep outer space.
Back on Earth, we have devices that employ magnetic fields to contain charged particles. Among them are the giant particle
accelerators that have been used to explore the substructure of matter. (See Figure 22.26.) Magnetic fields not only control the
direction of the charged particles, they also are used to focus particles into beams and overcome the repulsion of like charges in
these beams.

Figure 22.26 The Fermilab facility in Illinois has a large particle accelerator (the most powerful in the world until 2008) that employs magnetic fields
(magnets seen here in orange) to contain and direct its beam. This and other accelerators have been in use for several decades and have allowed us
to discover some of the laws underlying all matter. (credit: ammcrim, Flickr)
Thermonuclear fusion (like that occurring in the Sun) is a hope for a future clean energy source. One of the most promising
devices is the tokamak, which uses magnetic fields to contain (or trap) and direct the reactive charged particles. (See Figure
22.27.) Less exotic, but more immediately practical, amplifiers in microwave ovens use a magnetic field to contain oscillating
electrons. These oscillating electrons generate the microwaves sent into the oven.
Figure 22.27 Tokamaks such as the one shown in the figure are being studied with the goal of economical production of energy by nuclear fusion.
Magnetic fields in the doughnut-shaped device contain and direct the reactive charged particles. (credit: David Mellis, Flickr)
Mass spectrometers have a variety of designs, and many use magnetic fields to measure mass. The curvature of a charged
particle’s path in the field is related to its mass and is measured to obtain mass information. (See More Applications of
Magnetism.) Historically, such techniques were employed in the first direct observations of electron charge and mass. Today,
mass spectrometers (sometimes coupled with gas chromatographs) are used to determine the make-up and sequencing of large
biological molecules.
22.6 The Hall Effect
Learning Objectives
• Describe the Hall effect.
• Calculate the Hall emf across a current-carrying conductor.

We have seen effects of a magnetic field on free-moving charges. The magnetic field also affects charges moving in a conductor.
One result is the Hall effect, which has important implications and applications.
Figure 22.28 shows what happens to charges moving through a conductor in a magnetic field. The field is perpendicular to the
electron drift velocity and to the width of the conductor. Note that conventional current is to the right in both parts of the figure. In
part (a), electrons carry the current and move to the left. In part (b), positive charges carry the current and move to the right.
Moving electrons feel a magnetic force toward one side of the conductor, leaving a net positive charge on the other side. This
separation of charge creates a voltage ε , known as the Hall emf, across the conductor. The creation of a voltage across a
current-carrying conductor by a magnetic field is known as the Hall effect, after Edwin Hall, the American physicist who
discovered it in 1879.
Figure 22.28 The Hall effect. (a) Electrons move to the left in this flat conductor (conventional current to the right). The magnetic field is directly out of
the page, represented by circled dots; it exerts a force on the moving charges, causing a voltage ε , the Hall emf, across the conductor. (b) Positive
charges moving to the right (conventional current also to the right) are moved to the side, producing a Hall emf of the opposite sign, –ε . Thus, if the
direction of the field and current are known, the sign of the charge carriers can be determined from the Hall effect.
One very important use of the Hall effect is to determine whether positive or negative charges carries the current. Note that in
Figure 22.28(b), where positive charges carry the current, the Hall emf has the sign opposite to when negative charges carry the
current. Historically, the Hall effect was used to show that electrons carry current in metals and it also shows that positive
charges carry current in some semiconductors. The Hall effect is used today as a research tool to probe the movement of
charges, their drift velocities and densities, and so on, in materials. In 1980, it was discovered that the Hall effect is quantized, an
example of quantum behavior in a macroscopic object.
The Hall effect has other uses that range from the determination of blood flow rate to precision measurement of magnetic field
strength. To examine these quantitatively, we need an expression for the Hall emf, ε , across a conductor. Consider the balance
of forces on a moving charge in a situation where B , v , and l are mutually perpendicular, such as shown in Figure 22.29.
Although the magnetic force moves negative charges to one side, they cannot build up without limit. The electric field caused by
their separation opposes the magnetic force, F = qvB , and the electric force, Fe = qE , eventually grows to equal it. That is,
(22.10)qE = qvB
or
(22.11)E = vB.
Note that the electric field E is uniform across the conductor because the magnetic field B is uniform, as is the conductor. For
a uniform electric field, the relationship between electric field and voltage is E = ε / l , where l is the width of the conductor and
ε is the Hall emf. Entering this into the last expression gives
(22.12)ε
l
= vB.
Solving this for the Hall emf yields
(22.13)ε = Blv (B, v, and l, mutually perpendicular),
where ε is the Hall effect voltage across a conductor of width l through which charges move at a speed v .

Figure 22.29 The Hall emf ε produces an electric force that balances the magnetic force on the moving charges. The magnetic force produces
charge separation, which builds up until it is balanced by the electric force, an equilibrium that is quickly reached.
One of the most common uses of the Hall effect is in the measurement of magnetic field strength B . Such devices, called Hall
probes, can be made very small, allowing fine position mapping. Hall probes can also be made very accurate, usually
accomplished by careful calibration. Another application of the Hall effect is to measure fluid flow in any fluid that has free
charges (most do). (See Figure 22.30.) A magnetic field applied perpendicular to the flow direction produces a Hall emf ε as
shown. Note that the sign of ε depends not on the sign of the charges, but only on the directions of B and v . The magnitude
of the Hall emf is ε = Blv , where l is the pipe diameter, so that the average velocity v can be determined from ε providing
the other factors are known.
Figure 22.30 The Hall effect can be used to measure fluid flow in any fluid having free charges, such as blood. The Hall emf ε is measured across
the tube perpendicular to the applied magnetic field and is proportional to the average velocity v .
Example 22.3 Calculating the Hall emf: Hall Effect for Blood Flow
A Hall effect flow probe is placed on an artery, applying a 0.100-T magnetic field across it, in a setup similar to that in Figure
22.30. What is the Hall emf, given the vessel’s inside diameter is 4.00 mm and the average blood velocity is 20.0 cm/s?
Strategy
Because B , v , and l are mutually perpendicular, the equation ε = Blv can be used to find ε .
Solution
Entering the given values for B , v , and l gives
(22.14)ε = Blv = (0.100 T)⎛
⎝4.00×10−3
m⎞
⎠(0.200 m/s)
= 80.0 μV

Discussion
This is the average voltage output. Instantaneous voltage varies with pulsating blood flow. The voltage is small in this type of
measurement. ε is particularly difficult to measure, because there are voltages associated with heart action (ECG voltages)
that are on the order of millivolts. In practice, this difficulty is overcome by applying an AC magnetic field, so that the Hall emf
is AC with the same frequency. An amplifier can be very selective in picking out only the appropriate frequency, eliminating
signals and noise at other frequencies.
22.7 Magnetic Force on a Current-Carrying Conductor
Learning Objectives
• Describe the effects of a magnetic force on a current-carrying conductor.
• Calculate the magnetic force on a current-carrying conductor.
Because charges ordinarily cannot escape a conductor, the magnetic force on charges moving in a conductor is transmitted to
the conductor itself.
Figure 22.31 The magnetic field exerts a force on a current-carrying wire in a direction given by the right hand rule 1 (the same direction as that on the
individual moving charges). This force can easily be large enough to move the wire, since typical currents consist of very large numbers of moving
charges.
We can derive an expression for the magnetic force on a current by taking a sum of the magnetic forces on individual charges.
(The forces add because they are in the same direction.) The force on an individual charge moving at the drift velocity vd is
given by F = qvdB sin θ . Taking B to be uniform over a length of wire l and zero elsewhere, the total magnetic force on the
wire is then F = (qvdB sin θ)(N) , where N is the number of charge carriers in the section of wire of length l . Now,
N = nV , where n is the number of charge carriers per unit volume and V is the volume of wire in the field. Noting that
V = Al , where A is the cross-sectional area of the wire, then the force on the wire is F = (qvdB sin θ)(nAl) . Gathering
terms,
(22.15)F = (nqAvd)lB sin θ.
Because nqAvd = I (see Current),
(22.16)F = IlB sin θ
is the equation for magnetic force on a length l of wire carrying a current I in a uniform magnetic field B , as shown in Figure
22.32. If we divide both sides of this expression by l , we find that the magnetic force per unit length of wire in a uniform field is
F
l
= IB sin θ . The direction of this force is given by RHR-1, with the thumb in the direction of the current I . Then, with the
fingers in the direction of B , a perpendicular to the palm points in the direction of F , as in Figure 22.32.

Figure 22.32 The force on a current-carrying wire in a magnetic field is F = IlB sin θ . Its direction is given by RHR-1.
Example 22.4 Calculating Magnetic Force on a Current-Carrying Wire: A Strong Magnetic Field
Calculate the force on the wire shown in Figure 22.31, given B = 1.50 T , l = 5.00 cm , and I = 20.0 A .
Strategy
The force can be found with the given information by using F = IlB sin θ and noting that the angle θ between I and B
is 90º , so that sin θ = 1 .
Solution
Entering the given values into F = IlB sin θ yields
(22.17)F = IlB sin θ = (20.0 A)(0.0500 m)(1.50 T)(1).
The units for tesla are 1 T = N
A ⋅ m
; thus,
(22.18)F = 1.50 N.
Discussion
This large magnetic field creates a significant force on a small length of wire.
Magnetic force on current-carrying conductors is used to convert electric energy to work. (Motors are a prime example—they
employ loops of wire and are considered in the next section.) Magnetohydrodynamics (MHD) is the technical name given to a
clever application where magnetic force pumps fluids without moving mechanical parts. (See Figure 22.33.)
Figure 22.33 Magnetohydrodynamics. The magnetic force on the current passed through this fluid can be used as a nonmechanical pump.
A strong magnetic field is applied across a tube and a current is passed through the fluid at right angles to the field, resulting in a
force on the fluid parallel to the tube axis as shown. The absence of moving parts makes this attractive for moving a hot,
chemically active substance, such as the liquid sodium employed in some nuclear reactors. Experimental artificial hearts are

testing with this technique for pumping blood, perhaps circumventing the adverse effects of mechanical pumps. (Cell
membranes, however, are affected by the large fields needed in MHD, delaying its practical application in humans.) MHD
propulsion for nuclear submarines has been proposed, because it could be considerably quieter than conventional propeller
drives. The deterrent value of nuclear submarines is based on their ability to hide and survive a first or second nuclear strike. As
we slowly disassemble our nuclear weapons arsenals, the submarine branch will be the last to be decommissioned because of
this ability (See Figure 22.34.) Existing MHD drives are heavy and inefficient—much development work is needed.
Figure 22.34 An MHD propulsion system in a nuclear submarine could produce significantly less turbulence than propellers and allow it to run more
silently. The development of a silent drive submarine was dramatized in the book and the film The Hunt for Red October.
22.8 Torque on a Current Loop: Motors and Meters
Learning Objectives
• Describe how motors and meters work in terms of torque on a current loop.
• Calculate the torque on a current-carrying loop in a magnetic field.
Motors are the most common application of magnetic force on current-carrying wires. Motors have loops of wire in a magnetic
field. When current is passed through the loops, the magnetic field exerts torque on the loops, which rotates a shaft. Electrical
energy is converted to mechanical work in the process. (See Figure 22.35.)
Figure 22.35 Torque on a current loop. A current-carrying loop of wire attached to a vertically rotating shaft feels magnetic forces that produce a
clockwise torque as viewed from above.
Let us examine the force on each segment of the loop in Figure 22.35 to find the torques produced about the axis of the vertical
shaft. (This will lead to a useful equation for the torque on the loop.) We take the magnetic field to be uniform over the
rectangular loop, which has width w and height l . First, we note that the forces on the top and bottom segments are vertical
and, therefore, parallel to the shaft, producing no torque. Those vertical forces are equal in magnitude and opposite in direction,
so that they also produce no net force on the loop. Figure 22.36 shows views of the loop from above. Torque is defined as
τ = rF sin θ , where F is the force, r is the distance from the pivot that the force is applied, and θ is the angle between r
and F . As seen in Figure 22.36(a), right hand rule 1 gives the forces on the sides to be equal in magnitude and opposite in

direction, so that the net force is again zero. However, each force produces a clockwise torque. Since r = w / 2 , the torque on
each vertical segment is (w / 2)F sin θ , and the two add to give a total torque.
(22.19)τ = w
2
F sin θ + w
2
F sin θ = wF sin θ
Figure 22.36 Top views of a current-carrying loop in a magnetic field. (a) The equation for torque is derived using this view. Note that the perpendicular
to the loop makes an angle θ with the field that is the same as the angle between w / 2 and F . (b) The maximum torque occurs when θ is a right
angle and sin θ = 1 . (c) Zero (minimum) torque occurs when θ is zero and sin θ = 0 . (d) The torque reverses once the loop rotates past
θ = 0 .
Now, each vertical segment has a length l that is perpendicular to B , so that the force on each is F = IlB . Entering F into
the expression for torque yields
(22.20)τ = wIlB sin θ.
If we have a multiple loop of N turns, we get N times the torque of one loop. Finally, note that the area of the loop is A = wl ;
the expression for the torque becomes
(22.21)τ = NIAB sin θ.
This is the torque on a current-carrying loop in a uniform magnetic field. This equation can be shown to be valid for a loop of any
shape. The loop carries a current I , has N turns, each of area A , and the perpendicular to the loop makes an angle θ with
the field B . The net force on the loop is zero.
Example 22.5 Calculating Torque on a Current-Carrying Loop in a Strong Magnetic Field
Find the maximum torque on a 100-turn square loop of a wire of 10.0 cm on a side that carries 15.0 A of current in a 2.00-T
field.

Strategy
Torque on the loop can be found using τ = NIAB sin θ . Maximum torque occurs when θ = 90º and sin θ = 1 .
Solution
For sin θ = 1 , the maximum torque is
(22.22)τmax = NIAB.
Entering known values yields
(22.23)τmax = (100)(15.0 A)⎛
⎝0.100 m2⎞
⎠(2.00 T)
= 30.0 N ⋅ m.
Discussion
This torque is large enough to be useful in a motor.
The torque found in the preceding example is the maximum. As the coil rotates, the torque decreases to zero at θ = 0 . The
torque then reverses its direction once the coil rotates past θ = 0 . (See Figure 22.36(d).) This means that, unless we do
something, the coil will oscillate back and forth about equilibrium at θ = 0 . To get the coil to continue rotating in the same
direction, we can reverse the current as it passes through θ = 0 with automatic switches called brushes. (See Figure 22.37.)
Figure 22.37 (a) As the angular momentum of the coil carries it through θ = 0 , the brushes reverse the current to keep the torque clockwise. (b) The
coil will rotate continuously in the clockwise direction, with the current reversing each half revolution to maintain the clockwise torque.
Meters, such as those in analog fuel gauges on a car, are another common application of magnetic torque on a current-carrying
loop. Figure 22.38 shows that a meter is very similar in construction to a motor. The meter in the figure has its magnets shaped
to limit the effect of θ by making B perpendicular to the loop over a large angular range. Thus the torque is proportional to I
and not θ . A linear spring exerts a counter-torque that balances the current-produced torque. This makes the needle deflection
proportional to I . If an exact proportionality cannot be achieved, the gauge reading can be calibrated. To produce a
galvanometer for use in analog voltmeters and ammeters that have a low resistance and respond to small currents, we use a
large loop area A , high magnetic field B , and low-resistance coils.

Figure 22.38 Meters are very similar to motors but only rotate through a part of a revolution. The magnetic poles of this meter are shaped to keep the
component of B perpendicular to the loop constant, so that the torque does not depend on θ and the deflection against the return spring is
proportional only to the current I .
22.9 Magnetic Fields Produced by Currents: Ampere’s Law
Learning Objectives
• Calculate current that produces a magnetic field.
• Use the right-hand rule 2 to determine the direction of current or the direction of magnetic field loops.
• 2.D.2.1 The student is able to create a verbal or visual representation of a magnetic field around a long straight wire or
a pair of parallel wires. (S.P. 1.1)
• 3.C.3.2 The student is able to plan a data collection strategy appropriate to an investigation of the direction of the force
on a moving electrically charged object caused by a current in a wire in the context of a specific set of equipment and
instruments and analyze the resulting data to arrive at a conclusion. (S.P. 4.2, 5.1)
How much current is needed to produce a significant magnetic field, perhaps as strong as the Earth’s field? Surveyors will tell
you that overhead electric power lines create magnetic fields that interfere with their compass readings. Indeed, when Oersted
discovered in 1820 that a current in a wire affected a compass needle, he was not dealing with extremely large currents. How
does the shape of wires carrying current affect the shape of the magnetic field created? We noted earlier that a current loop
created a magnetic field similar to that of a bar magnet, but what about a straight wire or a toroid (doughnut)? How is the
direction of a current-created field related to the direction of the current? Answers to these questions are explored in this section,
together with a brief discussion of the law governing the fields created by currents.
Magnetic Field Created by a Long Straight Current-Carrying Wire: Right Hand Rule 2
Magnetic fields have both direction and magnitude. As noted before, one way to explore the direction of a magnetic field is with
compasses, as shown for a long straight current-carrying wire in Figure 22.39. Hall probes can determine the magnitude of the
field. The field around a long straight wire is found to be in circular loops. The right hand rule 2 (RHR-2) emerges from this
exploration and is valid for any current segment—point the thumb in the direction of the current, and the fingers curl in the
direction of the magnetic field loops created by it.

Figure 22.39 (a) Compasses placed near a long straight current-carrying wire indicate that field lines form circular loops centered on the wire. (b) Right
hand rule 2 states that, if the right hand thumb points in the direction of the current, the fingers curl in the direction of the field. This rule is consistent
with the field mapped for the long straight wire and is valid for any current segment.
Making Connections: Notation
For a wire oriented perpendicular to the page, if the current in the wire is directed out of the page, the right-hand rule tells us
that the magnetic field lines will be oriented in a counterclockwise direction around the wire. If the current in the wire is
directed into the page, the magnetic field lines will be oriented in a clockwise direction around the wire. We use ⊙ to
indicate that the direction of the current in the wire is out of the page, and ⊗ for the direction into the page.
Figure 22.40 Two parallel wires have currents pointing into or out of the page as shown. The direction of the magnetic field in the vicinity of the
two wires is shown.
The magnetic field strength (magnitude) produced by a long straight current-carrying wire is found by experiment to be
(22.24)
B =
µ0 I
2πr
(long straight wire),
where I is the current, r is the shortest distance to the wire, and the constant µ0 = 4π× 10−7
T ⋅ m/A is the permeability
of free space. (µ0 is one of the basic constants in nature. We will see later that µ0 is related to the speed of light.) Since the
wire is very long, the magnitude of the field depends only on distance from the wire r , not on position along the wire.

Example 22.6 Calculating Current that Produces a Magnetic Field
Find the current in a long straight wire that would produce a magnetic field twice the strength of the Earth’s at a distance of
5.0 cm from the wire.
Strategy
The Earth’s field is about 5.0×10−5
T , and so here B due to the wire is taken to be 1.0×10−4
T . The equation
B =
µ0 I
2πr
can be used to find I , since all other quantities are known.
Solution
Solving for I and entering known values gives
(22.25)
I = 2πrB
µ0
=
2π⎛
⎝5.0×10−2
m⎞
⎠
⎛
⎝1.0×10−4
T⎞
⎠
4π×10−7
T ⋅ m/A
= 25 A.
Discussion
So a moderately large current produces a significant magnetic field at a distance of 5.0 cm from a long straight wire. Note
that the answer is stated to only two digits, since the Earth’s field is specified to only two digits in this example.
Ampere’s Law and Others
The magnetic field of a long straight wire has more implications than you might at first suspect. Each segment of current
produces a magnetic field like that of a long straight wire, and the total field of any shape current is the vector sum of the fields
due to each segment. The formal statement of the direction and magnitude of the field due to each segment is called the Biot-
Savart law. Integral calculus is needed to sum the field for an arbitrary shape current. This results in a more complete law, called
Ampere’s law, which relates magnetic field and current in a general way. Ampere’s law in turn is a part of Maxwell’s equations,
which give a complete theory of all electromagnetic phenomena. Considerations of how Maxwell’s equations appear to different
observers led to the modern theory of relativity, and the realization that electric and magnetic fields are different manifestations of
the same thing. Most of this is beyond the scope of this text in both mathematical level, requiring calculus, and in the amount of
space that can be devoted to it. But for the interested student, and particularly for those who continue in physics, engineering, or
similar pursuits, delving into these matters further will reveal descriptions of nature that are elegant as well as profound. In this
text, we shall keep the general features in mind, such as RHR-2 and the rules for magnetic field lines listed in Magnetic Fields
and Magnetic Field Lines, while concentrating on the fields created in certain important situations.
Making Connections: Relativity
Hearing all we do about Einstein, we sometimes get the impression that he invented relativity out of nothing. On the contrary,
one of Einstein’s motivations was to solve difficulties in knowing how different observers see magnetic and electric fields.
Magnetic Field Produced by a Current-Carrying Circular Loop
The magnetic field near a current-carrying loop of wire is shown in Figure 22.41. Both the direction and the magnitude of the
magnetic field produced by a current-carrying loop are complex. RHR-2 can be used to give the direction of the field near the
loop, but mapping with compasses and the rules about field lines given in Magnetic Fields and Magnetic Field Lines are
needed for more detail. There is a simple formula for the magnetic field strength at the center of a circular loop. It is
(22.26)
B =
µ0 I
2R
(at center of loop),
where R is the radius of the loop. This equation is very similar to that for a straight wire, but it is valid only at the center of a
circular loop of wire. The similarity of the equations does indicate that similar field strength can be obtained at the center of a
loop. One way to get a larger field is to have N loops; then, the field is B = Nµ0I / (2R) . Note that the larger the loop, the
smaller the field at its center, because the current is farther away.

Figure 22.41 (a) RHR-2 gives the direction of the magnetic field inside and outside a current-carrying loop. (b) More detailed mapping with compasses
or with a Hall probe completes the picture. The field is similar to that of a bar magnet.
Magnetic Field Produced by a Current-Carrying Solenoid
A solenoid is a long coil of wire (with many turns or loops, as opposed to a flat loop). Because of its shape, the field inside a
solenoid can be very uniform, and also very strong. The field just outside the coils is nearly zero. Figure 22.42 shows how the
field looks and how its direction is given by RHR-2.
Figure 22.42 (a) Because of its shape, the field inside a solenoid of length l is remarkably uniform in magnitude and direction, as indicated by the
straight and uniformly spaced field lines. The field outside the coils is nearly zero. (b) This cutaway shows the magnetic field generated by the current
in the solenoid.
The magnetic field inside of a current-carrying solenoid is very uniform in direction and magnitude. Only near the ends does it
begin to weaken and change direction. The field outside has similar complexities to flat loops and bar magnets, but the magnetic
field strength inside a solenoid is simply
(22.27)B = µ0nI (inside a solenoid),
where n is the number of loops per unit length of the solenoid (n = N / l , with N being the number of loops and l the
length). Note that B is the field strength anywhere in the uniform region of the interior and not just at the center. Large uniform
fields spread over a large volume are possible with solenoids, as Example 22.7 implies.
Example 22.7 Calculating Field Strength inside a Solenoid
What is the field inside a 2.00-m-long solenoid that has 2000 loops and carries a 1600-A current?
Strategy

To find the field strength inside a solenoid, we use B = µ0nI . First, we note the number of loops per unit length is
(22.28)
n = N
l
= 2000
2.00 m
= 1000 m−1
= 10 cm−1
.
Solution
Substituting known values gives
(22.29)B = µ0nI = ⎛
⎝4π×10−7
T ⋅ m/A⎞
⎠
⎛
⎝1000 m−1⎞
⎠(1600 A)
= 2.01 T.
Discussion
This is a large field strength that could be established over a large-diameter solenoid, such as in medical uses of magnetic
resonance imaging (MRI). The very large current is an indication that the fields of this strength are not easily achieved,
however. Such a large current through 1000 loops squeezed into a meter’s length would produce significant heating. Higher
currents can be achieved by using superconducting wires, although this is expensive. There is an upper limit to the current,
since the superconducting state is disrupted by very large magnetic fields.
Applying the Science Practices: Charged Particle in a Magnetic Field
Visit here (http://openstaxcollege.org/l/31particlemagnetic) and start the simulation applet “Particle in a Magnetic Field
(2D)” in order to explore the magnetic force that acts on a charged particle in a magnetic field. Experiment with the
simulation to see how it works and what parameters you can change; then construct a plan to methodically investigate how
magnetic fields affect charged particles. Some questions you may want to answer as part of your experiment are:
• Are the paths of charged particles in magnetic fields always similar in two dimensions? Why or why not?
• How would the path of a neutral particle in the magnetic field compare to the path of a charged particle?
• How would the path of a positive particle differ from the path of a negative particle in a magnetic field?
• What quantities dictate the properties of the particle’s path?
• If you were attempting to measure the mass of a charged particle moving through a magnetic field, what would you
need to measure about its path? Would you need to see it moving at many different velocities or through different field
strengths, or would one trial be sufficient if your measurements were correct?
• Would doubling the charge change the path through the field? Predict an answer to this question, and then test your
hypothesis.
• Would doubling the velocity change the path through the field? Predict an answer to this question, and then test your
hypothesis.
• Would doubling the magnetic field strength change the path through the field? Predict an answer to this question, and
then test your hypothesis.
• Would increasing the mass change the path? Predict an answer to this question, and then test your hypothesis.
There are interesting variations of the flat coil and solenoid. For example, the toroidal coil used to confine the reactive particles in
tokamaks is much like a solenoid bent into a circle. The field inside a toroid is very strong but circular. Charged particles travel in
circles, following the field lines, and collide with one another, perhaps inducing fusion. But the charged particles do not cross field
lines and escape the toroid. A whole range of coil shapes are used to produce all sorts of magnetic field shapes. Adding
ferromagnetic materials produces greater field strengths and can have a significant effect on the shape of the field.
Ferromagnetic materials tend to trap magnetic fields (the field lines bend into the ferromagnetic material, leaving weaker fields
outside it) and are used as shields for devices that are adversely affected by magnetic fields, including the Earth’s magnetic field.
PhET Explorations: Generator
Generate electricity with a bar magnet! Discover the physics behind the phenomena by exploring magnets and how you can
use them to make a bulb light.
Figure 22.43 Generator (http://cnx.org/content/m55399/1.4/generator_en.jar)

22.10 Magnetic Force between Two Parallel Conductors
Learning Objectives
• Describe the effects of the magnetic force between two conductors.
• Calculate the force between two parallel conductors.
• 2.D.2.1 The student is able to create a verbal or visual representation of a magnetic field around a long straight wire or
a pair of parallel wires. (S.P. 1.1)
You might expect that there are significant forces between current-carrying wires, since ordinary currents produce significant
magnetic fields and these fields exert significant forces on ordinary currents. But you might not expect that the force between
wires is used to define the ampere. It might also surprise you to learn that this force has something to do with why large circuit
breakers burn up when they attempt to interrupt large currents.
The force between two long straight and parallel conductors separated by a distance r can be found by applying what we have
developed in preceding sections. Figure 22.44 shows the wires, their currents, the fields they create, and the subsequent forces
they exert on one another. Let us consider the field produced by wire 1 and the force it exerts on wire 2 (call the force F2 ). The
field due to I1 at a distance r is given to be
(22.30)
B1 =
µ0 I1
2πr
.
Figure 22.44 (a) The magnetic field produced by a long straight conductor is perpendicular to a parallel conductor, as indicated by RHR-2. (b) A view
from above of the two wires shown in (a), with one magnetic field line shown for each wire. RHR-1 shows that the force between the parallel
conductors is attractive when the currents are in the same direction. A similar analysis shows that the force is repulsive between currents in opposite
directions.
This field is uniform along wire 2 and perpendicular to it, and so the force F2 it exerts on wire 2 is given by F = IlB sin θ with
sin θ = 1 :
(22.31)F2 = I2lB1.
By Newton’s third law, the forces on the wires are equal in magnitude, and so we just write F for the magnitude of F2 . (Note
that F1 = −F2 .) Since the wires are very long, it is convenient to think in terms of F / l , the force per unit length. Substituting
the expression for B1 into the last equation and rearranging terms gives
(22.32)F
l
=
µ0 I1 I2
2πr
.
F / l is the force per unit length between two parallel currents I1 and I2 separated by a distance r . The force is attractive if
the currents are in the same direction and repulsive if they are in opposite directions.

Making Connections: Field Canceling
For two parallel wires, the fields will tend to cancel out in the area between the wires.
Figure 22.45 Two parallel wires have currents pointing in the same direction, out of the page. The direction of the magnetic fields induced by
each wire is shown.
Note that the magnetic influence of the wire on the left-hand side extends beyond the wire on the right-hand side. To the
right of both wires, the total magnetic field is directed toward the top of the page and is the result of the sum of the fields of
both wires. Obviously, the closer wire has a greater effect on the overall magnetic field, but the more distant wire also
contributes. One wire cannot block the magnetic field of another wire any more than a massive stone floor beneath you can
block the gravitational field of the Earth.
Parallel wires with currents in the same direction attract, as you can see if we isolate the magnetic field lines of wire 2
influencing the current in wire 1. Right-hand rule 1 tells us the direction of the resulting magnetic force.
Figure 22.46 The same two wires are shown, but now only a part of the magnetic field due to wire 2 is shown in order to demonstrate how the
magnetic force from wire 2 affects wire 1.
When the currents point in opposite directions as shown, the magnetic field in between the two wires is augmented. In the
region outside of the two wires, along the horizontal line connecting the wires, the magnetic fields partially cancel.
Figure 22.47 Two wires with parallel currents pointing in opposite directions are shown. The direction of the magnetic field due to each wire is
indicated.
Parallel wires with currents in opposite directions repel, as you can see if we isolate the magnetic field lines of wire 2
influencing the current in wire 1. Right-hand rule 1 tells us the direction of the resulting magnetic force.

Figure 22.48 The same two wires with opposite currents are shown, but now only a part of the magnetic field due to wire 2 is shown in order to
demonstrate how the magnetic force from wire 2 affects wire 1.
This force is responsible for the pinch effect in electric arcs and plasmas. The force exists whether the currents are in wires or
not. In an electric arc, where currents are moving parallel to one another, there is an attraction that squeezes currents into a
smaller tube. In large circuit breakers, like those used in neighborhood power distribution systems, the pinch effect can
concentrate an arc between plates of a switch trying to break a large current, burn holes, and even ignite the equipment. Another
example of the pinch effect is found in the solar plasma, where jets of ionized material, such as solar flares, are shaped by
magnetic forces.
The operational definition of the ampere is based on the force between current-carrying wires. Note that for parallel wires
separated by 1 meter with each carrying 1 ampere, the force per meter is
(22.33)
F
l
=
⎛
⎝4π×10−7
T ⋅ m/A⎞
⎠(1 A)2
(2π)(1 m)
= 2×10−7
N/m.
Since µ0 is exactly 4π×10−7
T ⋅ m/A by definition, and because 1 T = 1 N/(A ⋅ m) , the force per meter is exactly
2×10−7
N/m . This is the basis of the operational definition of the ampere.
The Ampere
The official definition of the ampere is:
One ampere of current through each of two parallel conductors of infinite length, separated by one meter in empty space
free of other magnetic fields, causes a force of exactly 2×10−7
N/m on each conductor.
Infinite-length straight wires are impractical and so, in practice, a current balance is constructed with coils of wire separated by a
few centimeters. Force is measured to determine current. This also provides us with a method for measuring the coulomb. We
measure the charge that flows for a current of one ampere in one second. That is, 1 C = 1 A ⋅ s . For both the ampere and the
coulomb, the method of measuring force between conductors is the most accurate in practice.
22.11 More Applications of Magnetism
Learning Objectives
• Describe some applications of magnetism.
Mass Spectrometry
The curved paths followed by charged particles in magnetic fields can be put to use. A charged particle moving perpendicular to
a magnetic field travels in a circular path having a radius r .
(22.34)r = mv
qB
It was noted that this relationship could be used to measure the mass of charged particles such as ions. A mass spectrometer is
a device that measures such masses. Most mass spectrometers use magnetic fields for this purpose, although some of them
have extremely sophisticated designs. Since there are five variables in the relationship, there are many possibilities. However, if
v , q , and B can be fixed, then the radius of the path r is simply proportional to the mass m of the charged particle. Let us
examine one such mass spectrometer that has a relatively simple design. (See Figure 22.49.) The process begins with an ion

source, a device like an electron gun. The ion source gives ions their charge, accelerates them to some velocity v , and directs a
beam of them into the next stage of the spectrometer. This next region is a velocity selector that only allows particles with a
particular value of v to get through.
Figure 22.49 This mass spectrometer uses a velocity selector to fix v so that the radius of the path is proportional to mass.
The velocity selector has both an electric field and a magnetic field, perpendicular to one another, producing forces in opposite
directions on the ions. Only those ions for which the forces balance travel in a straight line into the next region. If the forces
balance, then the electric force F = qE equals the magnetic force F = qvB , so that qE = qvB . Noting that q cancels, we
see that
(22.35)
v = E
B
is the velocity particles must have to make it through the velocity selector, and further, that v can be selected by varying E and
B . In the final region, there is only a uniform magnetic field, and so the charged particles move in circular arcs with radii
proportional to particle mass. The paths also depend on charge q , but since q is in multiples of electron charges, it is easy to
determine and to discriminate between ions in different charge states.
Mass spectrometry today is used extensively in chemistry and biology laboratories to identify chemical and biological substances
according to their mass-to-charge ratios. In medicine, mass spectrometers are used to measure the concentration of isotopes
used as tracers. Usually, biological molecules such as proteins are very large, so they are broken down into smaller fragments
before analyzing. Recently, large virus particles have been analyzed as a whole on mass spectrometers. Sometimes a gas
chromatograph or high-performance liquid chromatograph provides an initial separation of the large molecules, which are then
input into the mass spectrometer.
Cathode Ray Tubes—CRTs—and the Like
What do non-flat-screen TVs, old computer monitors, x-ray machines, and the 2-mile-long Stanford Linear Accelerator have in
common? All of them accelerate electrons, making them different versions of the electron gun. Many of these devices use
magnetic fields to steer the accelerated electrons. Figure 22.50 shows the construction of the type of cathode ray tube (CRT)
found in some TVs, oscilloscopes, and old computer monitors. Two pairs of coils are used to steer the electrons, one vertically
and the other horizontally, to their desired destination.

Figure 22.50 The cathode ray tube (CRT) is so named because rays of electrons originate at the cathode in the electron gun. Magnetic coils are used
to steer the beam in many CRTs. In this case, the beam is moved down. Another pair of horizontal coils would steer the beam horizontally.
Magnetic Resonance Imaging
Magnetic resonance imaging (MRI) is one of the most useful and rapidly growing medical imaging tools. It non-invasively
produces two-dimensional and three-dimensional images of the body that provide important medical information with none of the
hazards of x-rays. MRI is based on an effect called nuclear magnetic resonance (NMR) in which an externally applied
magnetic field interacts with the nuclei of certain atoms, particularly those of hydrogen (protons). These nuclei possess their own
small magnetic fields, similar to those of electrons and the current loops discussed earlier in this chapter.
When placed in an external magnetic field, such nuclei experience a torque that pushes or aligns the nuclei into one of two new
energy states—depending on the orientation of its spin (analogous to the N pole and S pole in a bar magnet). Transitions from
the lower to higher energy state can be achieved by using an external radio frequency signal to “flip” the orientation of the small
magnets. (This is actually a quantum mechanical process. The direction of the nuclear magnetic field is quantized as is energy in
the radio waves. We will return to these topics in later chapters.) The specific frequency of the radio waves that are absorbed and
reemitted depends sensitively on the type of nucleus, the chemical environment, and the external magnetic field strength.
Therefore, this is a resonance phenomenon in which nuclei in a magnetic field act like resonators (analogous to those discussed
in the treatment of sound in Oscillatory Motion and Waves) that absorb and reemit only certain frequencies. Hence, the
phenomenon is named nuclear magnetic resonance (NMR).
NMR has been used for more than 50 years as an analytical tool. It was formulated in 1946 by F. Bloch and E. Purcell, with the
1952 Nobel Prize in Physics going to them for their work. Over the past two decades, NMR has been developed to produce
detailed images in a process now called magnetic resonance imaging (MRI), a name coined to avoid the use of the word
“nuclear” and the concomitant implication that nuclear radiation is involved. (It is not.) The 2003 Nobel Prize in Medicine went to
P. Lauterbur and P. Mansfield for their work with MRI applications.
The largest part of the MRI unit is a superconducting magnet that creates a magnetic field, typically between 1 and 2 T in
strength, over a relatively large volume. MRI images can be both highly detailed and informative about structures and organ
functions. It is helpful that normal and non-normal tissues respond differently for slight changes in the magnetic field. In most
medical images, the protons that are hydrogen nuclei are imaged. (About 2/3 of the atoms in the body are hydrogen.) Their
location and density give a variety of medically useful information, such as organ function, the condition of tissue (as in the
brain), and the shape of structures, such as vertebral disks and knee-joint surfaces. MRI can also be used to follow the
movement of certain ions across membranes, yielding information on active transport, osmosis, dialysis, and other phenomena.
With excellent spatial resolution, MRI can provide information about tumors, strokes, shoulder injuries, infections, etc.
An image requires position information as well as the density of a nuclear type (usually protons). By varying the magnetic field
slightly over the volume to be imaged, the resonant frequency of the protons is made to vary with position. Broadcast radio
frequencies are swept over an appropriate range and nuclei absorb and reemit them only if the nuclei are in a magnetic field with
the correct strength. The imaging receiver gathers information through the body almost point by point, building up a tissue map.
The reception of reemitted radio waves as a function of frequency thus gives position information. These “slices” or cross
sections through the body are only several mm thick. The intensity of the reemitted radio waves is proportional to the
concentration of the nuclear type being flipped, as well as information on the chemical environment in that area of the body.
Various techniques are available for enhancing contrast in images and for obtaining more information. Scans called T1, T2, or
proton density scans rely on different relaxation mechanisms of nuclei. Relaxation refers to the time it takes for the protons to
return to equilibrium after the external field is turned off. This time depends upon tissue type and status (such as inflammation).
While MRI images are superior to x rays for certain types of tissue and have none of the hazards of x rays, they do not
completely supplant x-ray images. MRI is less effective than x rays for detecting breaks in bone, for example, and in imaging
breast tissue, so the two diagnostic tools complement each other. MRI images are also expensive compared to simple x-ray
images and tend to be used most often where they supply information not readily obtained from x rays. Another disadvantage of
MRI is that the patient is totally enclosed with detectors close to the body for about 30 minutes or more, leading to
claustrophobia. It is also difficult for the obese patient to be in the magnet tunnel. New “open-MRI” machines are now available in
which the magnet does not completely surround the patient.
Over the last decade, the development of much faster scans, called “functional MRI” (fMRI), has allowed us to map the
functioning of various regions in the brain responsible for thought and motor control. This technique measures the change in
blood flow for activities (thought, experiences, action) in the brain. The nerve cells increase their consumption of oxygen when
active. Blood hemoglobin releases oxygen to active nerve cells and has somewhat different magnetic properties when
oxygenated than when deoxygenated. With MRI, we can measure this and detect a blood oxygen-dependent signal. Most of the
brain scans today use fMRI.

Ampere’s law:
B-field:
Biot-Savart law:
Curie temperature:
direction of magnetic field lines:
domains:
electromagnet:
electromagnetism:
ferromagnetic:
gauss:
Hall effect:
Hall emf:
Lorentz force:
magnetic field:
Other Medical Uses of Magnetic Fields
Currents in nerve cells and the heart create magnetic fields like any other currents. These can be measured but with some
difficulty since their strengths are about 10−6
to 10−8
less than the Earth’s magnetic field. Recording of the heart’s magnetic
field as it beats is called a magnetocardiogram (MCG), while measurements of the brain’s magnetic field is called a
magnetoencephalogram (MEG). Both give information that differs from that obtained by measuring the electric fields of these
organs (ECGs and EEGs), but they are not yet of sufficient importance to make these difficult measurements common.
In both of these techniques, the sensors do not touch the body. MCG can be used in fetal studies, and is probably more sensitive
than echocardiography. MCG also looks at the heart’s electrical activity whose voltage output is too small to be recorded by
surface electrodes as in EKG. It has the potential of being a rapid scan for early diagnosis of cardiac ischemia (obstruction of
blood flow to the heart) or problems with the fetus.
MEG can be used to identify abnormal electrical discharges in the brain that produce weak magnetic signals. Therefore, it looks
at brain activity, not just brain structure. It has been used for studies of Alzheimer’s disease and epilepsy. Advances in
instrumentation to measure very small magnetic fields have allowed these two techniques to be used more in recent years. What
is used is a sensor called a SQUID, for superconducting quantum interference device. This operates at liquid helium
temperatures and can measure magnetic fields thousands of times smaller than the Earth’s.
Finally, there is a burgeoning market for magnetic cures in which magnets are applied in a variety of ways to the body, from
magnetic bracelets to magnetic mattresses. The best that can be said for such practices is that they are apparently harmless,
unless the magnets get close to the patient’s computer or magnetic storage disks. Claims are made for a broad spectrum of
benefits from cleansing the blood to giving the patient more energy, but clinical studies have not verified these claims, nor is
there an identifiable mechanism by which such benefits might occur.
PhET Explorations: Magnet and Compass
Ever wonder how a compass worked to point you to the Arctic? Explore the interactions between a compass and bar
magnet, and then add the Earth and find the surprising answer! Vary the magnet's strength, and see how things change both
inside and outside. Use the field meter to measure how the magnetic field changes.
Figure 22.51 Magnet and Compass (http://cnx.org/content/m55403/1.2/magnet-and-compass_en.jar)
Glossary
the physical law that states that the magnetic field around an electric current is proportional to the current;
each segment of current produces a magnetic field like that of a long straight wire, and the total field of any shape
current is the vector sum of the fields due to each segment
another term for magnetic field
a physical law that describes the magnetic field generated by an electric current in terms of a specific
equation
the temperature above which a ferromagnetic material cannot be magnetized
the direction that the north end of a compass needle points
regions within a material that behave like small bar magnets
an object that is temporarily magnetic when an electrical current is passed through it
the use of electrical currents to induce magnetism
materials, such as iron, cobalt, nickel, and gadolinium, that exhibit strong magnetic effects
G, the unit of the magnetic field strength; 1 G = 10–4
T
the creation of voltage across a current-carrying conductor by a magnetic field
the electromotive force created by a current-carrying conductor by a magnetic field, ε = Blv
the force on a charge moving in a magnetic field
the representation of magnetic forces

magnetic field lines:
magnetic field strength (magnitude) produced by a long straight current-carrying wire:
magnetic field strength at the center of a circular loop:
magnetic field strength inside a solenoid:
magnetic force:
magnetic monopoles:
magnetic resonance imaging (MRI):
magnetized:
magnetocardiogram (MCG):
magnetoencephalogram (MEG):
Maxwell’s equations:
meter:
motor:
north magnetic pole:
nuclear magnetic resonance (NMR):
permeability of free space:
right hand rule 1 (RHR-1):
right hand rule 2 (RHR-2):
solenoid:
south magnetic pole:
tesla:
the pictorial representation of the strength and the direction of a magnetic field
defined as B =
µ0 I
2πr
, where I
is the current, r is the shortest distance to the wire, and µ0 is the permeability of free space
defined as B =
µ0 I
2R
where R is the radius of the loop
defined as B = µ0nI where n is the number of loops per unit length of the
solenoid (n = N / l , with N being the number of loops and l the length)
the force on a charge produced by its motion through a magnetic field; the Lorentz force
an isolated magnetic pole; a south pole without a north pole, or vice versa (no magnetic monopole has
ever been observed)
a medical imaging technique that uses magnetic fields create detailed images of
internal tissues and organs
to be turned into a magnet; to be induced to be magnetic
a recording of the heart’s magnetic field as it beats
a measurement of the brain’s magnetic field
a set of four equations that describe electromagnetic phenomena
common application of magnetic torque on a current-carrying loop that is very similar in construction to a motor; by
design, the torque is proportional to I and not θ , so the needle deflection is proportional to the current
loop of wire in a magnetic field; when current is passed through the loops, the magnetic field exerts torque on the
loops, which rotates a shaft; electrical energy is converted to mechanical work in the process
the end or the side of a magnet that is attracted toward Earth’s geographic north pole
a phenomenon in which an externally applied magnetic field interacts with the nuclei of
certain atoms
the measure of the ability of a material, in this case free space, to support a magnetic field; the
constant µ0 = 4π×10−7
T ⋅ m/A
the rule to determine the direction of the magnetic force on a positive moving charge: when the
thumb of the right hand points in the direction of the charge’s velocity v and the fingers point in the direction of the
magnetic field B , then the force on the charge is perpendicular and away from the palm; the force on a negative charge
is perpendicular and into the palm
a rule to determine the direction of the magnetic field induced by a current-carrying wire: Point the
thumb of the right hand in the direction of current, and the fingers curl in the direction of the magnetic field loops
a thin wire wound into a coil that produces a magnetic field when an electric current is passed through it
the end or the side of a magnet that is attracted toward Earth’s geographic south pole
T, the SI unit of the magnetic field strength; 1 T = 1 N
A ⋅ m
Section Summary
22.1 Magnets
• Magnetism is a subject that includes the properties of magnets, the effect of the magnetic force on moving charges and
currents, and the creation of magnetic fields by currents.
• There are two types of magnetic poles, called the north magnetic pole and south magnetic pole.
• North magnetic poles are those that are attracted toward the Earth’s geographic north pole.
• Like poles repel and unlike poles attract.
• Magnetic poles always occur in pairs of north and south—it is not possible to isolate north and south poles.

• Magnetic poles always occur in pairs of north and south—it is not possible to isolate north and south poles.
• All magnetism is created by electric current.
• Ferromagnetic materials, such as iron, are those that exhibit strong magnetic effects.
• The atoms in ferromagnetic materials act like small magnets (due to currents within the atoms) and can be aligned, usually
in millimeter-sized regions called domains.
• Domains can grow and align on a larger scale, producing permanent magnets. Such a material is magnetized, or induced
to be magnetic.
• Above a material’s Curie temperature, thermal agitation destroys the alignment of atoms, and ferromagnetism disappears.
• Electromagnets employ electric currents to make magnetic fields, often aided by induced fields in ferromagnetic materials.
• Magnetic fields can be pictorially represented by magnetic field lines, the properties of which are as follows:
1. The field is tangent to the magnetic field line.
2. Field strength is proportional to the line density.
3. Field lines cannot cross.
4. Field lines are continuous loops.
• Magnetic fields exert a force on a moving charge q, the magnitude of which is
F = qvB sin θ,
where θ is the angle between the directions of v and B .
• The SI unit for magnetic field strength B is the tesla (T), which is related to other units by
1 T = 1 N
C ⋅ m/s
= 1 N
A ⋅ m
.
• The direction of the force on a moving charge is given by right hand rule 1 (RHR-1): Point the thumb of the right hand in the
direction of v , the fingers in the direction of B , and a perpendicular to the palm points in the direction of F .
• The force is perpendicular to the plane formed by v and B . Since the force is zero if v is parallel to B , charged
particles often follow magnetic field lines rather than cross them.
• Magnetic force can supply centripetal force and cause a charged particle to move in a circular path of radius
r = mv
qB
,
where v is the component of the velocity perpendicular to B for a charged particle with mass m and charge q .
• The Hall effect is the creation of voltage ε , known as the Hall emf, across a current-carrying conductor by a magnetic field.
• The Hall emf is given by
ε = Blv (B, v, and l, mutually perpendicular)
for a conductor of width l through which charges move at a speed v .
• The magnetic force on current-carrying conductors is given by
F = IlB sin θ,
where I is the current, l is the length of a straight conductor in a uniform magnetic field B , and θ is the angle between
I and B . The force follows RHR-1 with the thumb in the direction of I .
• The torque τ on a current-carrying loop of any shape in a uniform magnetic field. is
τ = NIAB sin θ,
where N is the number of turns, I is the current, A is the area of the loop, B is the magnetic field strength, and θ is
the angle between the perpendicular to the loop and the magnetic field.

• The strength of the magnetic field created by current in a long straight wire is given by
B =
µ0 I
2πr
(long straight wire),
I is the current, r is the shortest distance to the wire, and the constant µ0 = 4π× 10−7
T ⋅ m/A is the permeability of
free space.
• The direction of the magnetic field created by a long straight wire is given by right hand rule 2 (RHR-2): Point the thumb of
the right hand in the direction of current, and the fingers curl in the direction of the magnetic field loops created by it.
• The magnetic field created by current following any path is the sum (or integral) of the fields due to segments along the
path (magnitude and direction as for a straight wire), resulting in a general relationship between current and field known as
Ampere’s law.
• The magnetic field strength at the center of a circular loop is given by
B =
µ0 I
2R
(at center of loop),
R is the radius of the loop. This equation becomes B = µ0nI / (2R) for a flat coil of N loops. RHR-2 gives the direction
of the field about the loop. A long coil is called a solenoid.
• The magnetic field strength inside a solenoid is
B = µ0nI (inside a solenoid),
where n is the number of loops per unit length of the solenoid. The field inside is very uniform in magnitude and direction.
• The force between two parallel currents I1 and I2 , separated by a distance r , has a magnitude per unit length given by
F
l
=
µ0 I1 I2
2πr
.
• The force is attractive if the currents are in the same direction, repulsive if they are in opposite directions.
• Crossed (perpendicular) electric and magnetic fields act as a velocity filter, giving equal and opposite forces on any charge
with velocity perpendicular to the fields and of magnitude
v = E
B
.
Conceptual Questions
22.1 Magnets
1. Volcanic and other such activity at the mid-Atlantic ridge extrudes material to fill the gap between separating tectonic plates
associated with continental drift. The magnetization of rocks is found to reverse in a coordinated manner with distance from the
ridge. What does this imply about the Earth’s magnetic field and how could the knowledge of the spreading rate be used to give
its historical record?
2. Explain why the magnetic field would not be unique (that is, not have a single value) at a point in space where magnetic field
lines might cross. (Consider the direction of the field at such a point.)
3. List the ways in which magnetic field lines and electric field lines are similar. For example, the field direction is tangent to the
line at any point in space. Also list the ways in which they differ. For example, electric force is parallel to electric field lines,
whereas magnetic force on moving charges is perpendicular to magnetic field lines.
4. Noting that the magnetic field lines of a bar magnet resemble the electric field lines of a pair of equal and opposite charges, do
you expect the magnetic field to rapidly decrease in strength with distance from the magnet? Is this consistent with your
experience with magnets?
5. Is the Earth’s magnetic field parallel to the ground at all locations? If not, where is it parallel to the surface? Is its strength the
same at all locations? If not, where is it greatest?
6. If a charged particle moves in a straight line through some region of space, can you say that the magnetic field in that region is
necessarily zero?

7. How can the motion of a charged particle be used to distinguish between a magnetic and an electric field?
8. High-velocity charged particles can damage biological cells and are a component of radiation exposure in a variety of locations
ranging from research facilities to natural background. Describe how you could use a magnetic field to shield yourself.
9. If a cosmic ray proton approaches the Earth from outer space along a line toward the center of the Earth that lies in the plane
of the equator, in what direction will it be deflected by the Earth’s magnetic field? What about an electron? A neutron?
10. What are the signs of the charges on the particles in Figure 22.52?
Figure 22.52
11. Which of the particles in Figure 22.53 has the greatest velocity, assuming they have identical charges and masses?
Figure 22.53
12. Which of the particles in Figure 22.53 has the greatest mass, assuming all have identical charges and velocities?
13. While operating, a high-precision TV monitor is placed on its side during maintenance. The image on the monitor changes
color and blurs slightly. Discuss the possible relation of these effects to the Earth’s magnetic field.
14. Discuss how the Hall effect could be used to obtain information on free charge density in a conductor. (Hint: Consider how
drift velocity and current are related.)
15. Draw a sketch of the situation in Figure 22.31 showing the direction of electrons carrying the current, and use RHR-1 to
verify the direction of the force on the wire.
16. Verify that the direction of the force in an MHD drive, such as that in Figure 22.33, does not depend on the sign of the
charges carrying the current across the fluid.
17. Why would a magnetohydrodynamic drive work better in ocean water than in fresh water? Also, why would superconducting
magnets be desirable?
18. Which is more likely to interfere with compass readings, AC current in your refrigerator or DC current when you start your
car? Explain.
19. Draw a diagram and use RHR-1 to show that the forces on the top and bottom segments of the motor’s current loop in
Figure 22.35 are vertical and produce no torque about the axis of rotation.
20. Make a drawing and use RHR-2 to find the direction of the magnetic field of a current loop in a motor (such as in Figure
22.35). Then show that the direction of the torque on the loop is the same as produced by like poles repelling and unlike poles
attracting.
21. Is the force attractive or repulsive between the hot and neutral lines hung from power poles? Why?

22. If you have three parallel wires in the same plane, as in Figure 22.54, with currents in the outer two running in opposite
directions, is it possible for the middle wire to be repelled by both? Attracted by both? Explain.
Figure 22.54 Three parallel coplanar wires with currents in the outer two in opposite directions.
23. Suppose two long straight wires run perpendicular to one another without touching. Does one exert a net force on the other?
If so, what is its direction? Does one exert a net torque on the other? If so, what is its direction? Justify your responses by using
the right hand rules.
24. Use the right hand rules to show that the force between the two loops in Figure 22.55 is attractive if the currents are in the
same direction and repulsive if they are in opposite directions. Is this consistent with like poles of the loops repelling and unlike
poles of the loops attracting? Draw sketches to justify your answers.
Figure 22.55 Two loops of wire carrying currents can exert forces and torques on one another.
25. If one of the loops in Figure 22.55 is tilted slightly relative to the other and their currents are in the same direction, what are
the directions of the torques they exert on each other? Does this imply that the poles of the bar magnet-like fields they create will
line up with each other if the loops are allowed to rotate?
26. Electric field lines can be shielded by the Faraday cage effect. Can we have magnetic shielding? Can we have gravitational
shielding?
27. Measurements of the weak and fluctuating magnetic fields associated with brain activity are called magnetoencephalograms
(MEGs). Do the brain’s magnetic fields imply coordinated or uncoordinated nerve impulses? Explain.
28. Discuss the possibility that a Hall voltage would be generated on the moving heart of a patient during MRI imaging. Also
discuss the same effect on the wires of a pacemaker. (The fact that patients with pacemakers are not given MRIs is significant.)
29. A patient in an MRI unit turns his head quickly to one side and experiences momentary dizziness and a strange taste in his
mouth. Discuss the possible causes.
30. You are told that in a certain region there is either a uniform electric or magnetic field. What measurement or observation
could you make to determine the type? (Ignore the Earth’s magnetic field.)
31. An example of magnetohydrodynamics (MHD) comes from the flow of a river (salty water). This fluid interacts with the Earth’s
magnetic field to produce a potential difference between the two river banks. How would you go about calculating the potential
difference?

32. Draw gravitational field lines between 2 masses, electric field lines between a positive and a negative charge, electric field
lines between 2 positive charges and magnetic field lines around a magnet. Qualitatively describe the differences between the
fields and the entities responsible for the field lines.

Problems & Exercises
22.4 Magnetic Field Strength: Force on a
Moving Charge in a Magnetic Field
1. What is the direction of the magnetic force on a positive
charge that moves as shown in each of the six cases shown
in Figure 22.56?
Figure 22.56
2. Repeat Exercise 22.1 for a negative charge.
3. What is the direction of the velocity of a negative charge
that experiences the magnetic force shown in each of the
three cases in Figure 22.57, assuming it moves
perpendicular to B?
Figure 22.57
4. Repeat Exercise 22.3 for a positive charge.
5. What is the direction of the magnetic field that produces the
magnetic force on a positive charge as shown in each of the
three cases in the figure below, assuming B is perpendicular
to v ?
Figure 22.58
6. Repeat Exercise 22.5 for a negative charge.
7. What is the maximum force on an aluminum rod with a
0.100-μC charge that you pass between the poles of a
1.50-T permanent magnet at a speed of 5.00 m/s? In what
direction is the force?
8. (a) Aircraft sometimes acquire small static charges.
Suppose a supersonic jet has a 0.500-μC charge and flies
due west at a speed of 660 m/s over the Earth’s south
magnetic pole, where the 8.00×10−5
-T magnetic field
points straight up. What are the direction and the magnitude
of the magnetic force on the plane? (b) Discuss whether the
value obtained in part (a) implies this is a significant or
negligible effect.
9. (a) A cosmic ray proton moving toward the Earth at
5.00×107
m/s experiences a magnetic force of
1.70×10−16
N . What is the strength of the magnetic field if
there is a 45º angle between it and the proton’s velocity? (b)
Is the value obtained in part (a) consistent with the known
strength of the Earth’s magnetic field on its surface? Discuss.
10. An electron moving at 4.00×103
m/s in a 1.25-T
magnetic field experiences a magnetic force of
1.40×10−16
N . What angle does the velocity of the
electron make with the magnetic field? There are two
answers.
11. (a) A physicist performing a sensitive measurement wants
to limit the magnetic force on a moving charge in her
equipment to less than 1.00×10−12
N . What is the
greatest the charge can be if it moves at a maximum speed of
30.0 m/s in the Earth’s field? (b) Discuss whether it would be
difficult to limit the charge to less than the value found in (a)
by comparing it with typical static electricity and noting that
static is often absent.
22.5 Force on a Moving Charge in a Magnetic
Field: Examples and Applications
If you need additional support for these problems, see More
Applications of Magnetism.
12. A cosmic ray electron moves at 7.50×106
m/s
perpendicular to the Earth’s magnetic field at an altitude
where field strength is 1.00×10−5
T . What is the radius of
the circular path the electron follows?
13. A proton moves at 7.50×107
m/s perpendicular to a
magnetic field. The field causes the proton to travel in a
circular path of radius 0.800 m. What is the field strength?
14. (a) Viewers of Star Trek hear of an antimatter drive on the
Starship Enterprise. One possibility for such a futuristic
energy source is to store antimatter charged particles in a
vacuum chamber, circulating in a magnetic field, and then
extract them as needed. Antimatter annihilates with normal
matter, producing pure energy. What strength magnetic field
is needed to hold antiprotons, moving at 5.00×107
m/s in a
circular path 2.00 m in radius? Antiprotons have the same
mass as protons but the opposite (negative) charge. (b) Is
this field strength obtainable with today’s technology or is it a
futuristic possibility?

15. (a) An oxygen-16 ion with a mass of 2.66×10−26
kg
travels at 5.00×106
m/s perpendicular to a 1.20-T
magnetic field, which makes it move in a circular arc with a
0.231-m radius. What positive charge is on the ion? (b) What
is the ratio of this charge to the charge of an electron? (c)
Discuss why the ratio found in (b) should be an integer.
16. What radius circular path does an electron travel if it
moves at the same speed and in the same magnetic field as
the proton in Exercise 22.13?
17. A velocity selector in a mass spectrometer uses a 0.100-T
magnetic field. (a) What electric field strength is needed to
select a speed of 4.00 x 106
m/s? (b) What is the voltage
between the plates if they are separated by 1.00 cm?
18. An electron in a TV CRT moves with a speed of
6.00×107
m/s , in a direction perpendicular to the Earth’s
field, which has a strength of 5.00×10−5
T . (a) What
strength electric field must be applied perpendicular to the
Earth’s field to make the electron moves in a straight line? (b)
If this is done between plates separated by 1.00 cm, what is
the voltage applied? (Note that TVs are usually surrounded
by a ferromagnetic material to shield against external
magnetic fields and avoid the need for such a correction.)
19. (a) At what speed will a proton move in a circular path of
the same radius as the electron in Exercise 22.12? (b) What
would the radius of the path be if the proton had the same
speed as the electron? (c) What would the radius be if the
proton had the same kinetic energy as the electron? (d) The
same momentum?
20. A mass spectrometer is being used to separate common
oxygen-16 from the much rarer oxygen-18, taken from a
sample of old glacial ice. (The relative abundance of these
oxygen isotopes is related to climatic temperature at the time
the ice was deposited.) The ratio of the masses of these two
ions is 16 to 18, the mass of oxygen-16 is 2.66×10−26
kg,
and they are singly charged and travel at 5.00×106
m/s in
a 1.20-T magnetic field. What is the separation between their
paths when they hit a target after traversing a semicircle?
21. (a) Triply charged uranium-235 and uranium-238 ions are
being separated in a mass spectrometer. (The much rarer
uranium-235 is used as reactor fuel.) The masses of the ions
are 3.90×10−25
kg and 3.95×10−25
kg , respectively,
and they travel at 3.00×105
m/s in a 0.250-T field. What is
the separation between their paths when they hit a target
after traversing a semicircle? (b) Discuss whether this
distance between their paths seems to be big enough to be
practical in the separation of uranium-235 from uranium-238.
22. A large water main is 2.50 m in diameter and the average
water velocity is 6.00 m/s. Find the Hall voltage produced if
the pipe runs perpendicular to the Earth’s 5.00×10−5
-T
field.
23. What Hall voltage is produced by a 0.200-T field applied
across a 2.60-cm-diameter aorta when blood velocity is 60.0
cm/s?
24. (a) What is the speed of a supersonic aircraft with a
17.0-m wingspan, if it experiences a 1.60-V Hall voltage
between its wing tips when in level flight over the north
magnetic pole, where the Earth’s field strength is
8.00×10−5
T? (b) Explain why very little current flows as a
result of this Hall voltage.
25. A nonmechanical water meter could utilize the Hall effect
by applying a magnetic field across a metal pipe and
measuring the Hall voltage produced. What is the average
fluid velocity in a 3.00-cm-diameter pipe, if a 0.500-T field
across it creates a 60.0-mV Hall voltage?
26. Calculate the Hall voltage induced on a patient’s heart
while being scanned by an MRI unit. Approximate the
conducting path on the heart wall by a wire 7.50 cm long that
moves at 10.0 cm/s perpendicular to a 1.50-T magnetic field.
27. A Hall probe calibrated to read 1.00 μV when placed in
a 2.00-T field is placed in a 0.150-T field. What is its output
voltage?
28. Using information in Example 20.6, what would the Hall
voltage be if a 2.00-T field is applied across a 10-gauge
copper wire (2.588 mm in diameter) carrying a 20.0-A
current?
29. Show that the Hall voltage across wires made of the same
material, carrying identical currents, and subjected to the
same magnetic field is inversely proportional to their
diameters. (Hint: Consider how drift velocity depends on wire
diameter.)
30. A patient with a pacemaker is mistakenly being scanned
for an MRI image. A 10.0-cm-long section of pacemaker wire
moves at a speed of 10.0 cm/s perpendicular to the MRI
unit’s magnetic field and a 20.0-mV Hall voltage is induced.
What is the magnetic field strength?
22.7 Magnetic Force on a Current-Carrying
Conductor
31. What is the direction of the magnetic force on the current
in each of the six cases in Figure 22.59?
Figure 22.59
32. What is the direction of a current that experiences the
magnetic force shown in each of the three cases in Figure
22.60, assuming the current runs perpendicular to B ?

Figure 22.60
33. What is the direction of the magnetic field that produces
the magnetic force shown on the currents in each of the three
cases in Figure 22.61, assuming B is perpendicular to I ?
Figure 22.61
34. (a) What is the force per meter on a lightning bolt at the
equator that carries 20,000 A perpendicular to the Earth’s
3.00×10−5
-T field? (b) What is the direction of the force if
the current is straight up and the Earth’s field direction is due
north, parallel to the ground?
35. (a) A DC power line for a light-rail system carries 1000 A
at an angle of 30.0º to the Earth’s 5.00×10−5
-T field.
What is the force on a 100-m section of this line? (b) Discuss
practical concerns this presents, if any.
36. What force is exerted on the water in an MHD drive
utilizing a 25.0-cm-diameter tube, if 100-A current is passed
across the tube that is perpendicular to a 2.00-T magnetic
field? (The relatively small size of this force indicates the
need for very large currents and magnetic fields to make
practical MHD drives.)
37. A wire carrying a 30.0-A current passes between the
poles of a strong magnet that is perpendicular to its field and
experiences a 2.16-N force on the 4.00 cm of wire in the field.
What is the average field strength?
38. (a) A 0.750-m-long section of cable carrying current to a
car starter motor makes an angle of 60º with the Earth’s
5.50×10−5
T field. What is the current when the wire
experiences a force of 7.00×10−3
N ? (b) If you run the
wire between the poles of a strong horseshoe magnet,
subjecting 5.00 cm of it to a 1.75-T field, what force is exerted
on this segment of wire?
39. (a) What is the angle between a wire carrying an 8.00-A
current and the 1.20-T field it is in if 50.0 cm of the wire
experiences a magnetic force of 2.40 N? (b) What is the force
on the wire if it is rotated to make an angle of 90º with the
field?
40. The force on the rectangular loop of wire in the magnetic
field in Figure 22.62 can be used to measure field strength.
The field is uniform, and the plane of the loop is perpendicular
to the field. (a) What is the direction of the magnetic force on
the loop? Justify the claim that the forces on the sides of the
loop are equal and opposite, independent of how much of the
loop is in the field and do not affect the net force on the loop.
(b) If a current of 5.00 A is used, what is the force per tesla on
the 20.0-cm-wide loop?
Figure 22.62 A rectangular loop of wire carrying a current is
perpendicular to a magnetic field. The field is uniform in the region
shown and is zero outside that region.
22.8 Torque on a Current Loop: Motors and
Meters
41. (a) By how many percent is the torque of a motor
decreased if its permanent magnets lose 5.0% of their
strength? (b) How many percent would the current need to be
increased to return the torque to original values?
42. (a) What is the maximum torque on a 150-turn square
loop of wire 18.0 cm on a side that carries a 50.0-A current in
a 1.60-T field? (b) What is the torque when θ is 10.9º?
43. Find the current through a loop needed to create a
maximum torque of 9.00 N ⋅ m. The loop has 50 square
turns that are 15.0 cm on a side and is in a uniform 0.800-T
magnetic field.
44. Calculate the magnetic field strength needed on a
200-turn square loop 20.0 cm on a side to create a maximum
torque of 300 N ⋅ m if the loop is carrying 25.0 A.
45. Since the equation for torque on a current-carrying loop is
τ = NIAB sin θ , the units of N ⋅ m must equal units of
A ⋅ m2
T . Verify this.
46. (a) At what angle θ is the torque on a current loop 90.0%
of maximum? (b) 50.0% of maximum? (c) 10.0% of
maximum?
47. A proton has a magnetic field due to its spin on its axis.
The field is similar to that created by a circular current loop
0.650×10−15
m in radius with a current of 1.05×104
A
(no kidding). Find the maximum torque on a proton in a
2.50-T field. (This is a significant torque on a small particle.)

48. (a) A 200-turn circular loop of radius 50.0 cm is vertical,
with its axis on an east-west line. A current of 100 A circulates
clockwise in the loop when viewed from the east. The Earth’s
field here is due north, parallel to the ground, with a strength
of 3.00×10−5
T . What are the direction and magnitude of
the torque on the loop? (b) Does this device have any
practical applications as a motor?
49. Repeat Exercise 22.41, but with the loop lying flat on the
ground with its current circulating counterclockwise (when
viewed from above) in a location where the Earth’s field is
north, but at an angle 45.0º below the horizontal and with a
strength of 6.00×10−5
T .
22.10 Magnetic Force between Two Parallel
Conductors
50. (a) The hot and neutral wires supplying DC power to a
light-rail commuter train carry 800 A and are separated by
75.0 cm. What is the magnitude and direction of the force
between 50.0 m of these wires? (b) Discuss the practical
consequences of this force, if any.
51. The force per meter between the two wires of a jumper
cable being used to start a stalled car is 0.225 N/m. (a) What
is the current in the wires, given they are separated by 2.00
cm? (b) Is the force attractive or repulsive?
52. A 2.50-m segment of wire supplying current to the motor
of a submerged submarine carries 1000 A and feels a 4.00-N
repulsive force from a parallel wire 5.00 cm away. What is the
direction and magnitude of the current in the other wire?
53. The wire carrying 400 A to the motor of a commuter train
feels an attractive force of 4.00×10−3
N/m due to a
parallel wire carrying 5.00 A to a headlight. (a) How far apart
are the wires? (b) Are the currents in the same direction?
54. An AC appliance cord has its hot and neutral wires
separated by 3.00 mm and carries a 5.00-A current. (a) What
is the average force per meter between the wires in the cord?
(b) What is the maximum force per meter between the wires?
(c) Are the forces attractive or repulsive? (d) Do appliance
cords need any special design features to compensate for
these forces?
55. Figure 22.63 shows a long straight wire near a
rectangular current loop. What is the direction and magnitude
of the total force on the loop?
Figure 22.63
56. Find the direction and magnitude of the force that each
wire experiences in Figure 22.64(a) by, using vector addition.
Figure 22.64
57. Find the direction and magnitude of the force that each
wire experiences in Figure 22.64(b), using vector addition.
58. Indicate whether the magnetic field created in each of the
three situations shown in Figure 22.65 is into or out of the
page on the left and right of the current.
Figure 22.65
59. What are the directions of the fields in the center of the
loop and coils shown in Figure 22.66?
Figure 22.66
60. What are the directions of the currents in the loop and
coils shown in Figure 22.67?
Figure 22.67
61. To see why an MRI utilizes iron to increase the magnetic
field created by a coil, calculate the current needed in a
400-loop-per-meter circular coil 0.660 m in radius to create a
1.20-T field (typical of an MRI instrument) at its center with no
iron present. The magnetic field of a proton is approximately
like that of a circular current loop 0.650×10−15
m in radius
carrying 1.05×104
A . What is the field at the center of such
a loop?
62. Inside a motor, 30.0 A passes through a 250-turn circular
loop that is 10.0 cm in radius. What is the magnetic field
strength created at its center?

63. Nonnuclear submarines use batteries for power when
submerged. (a) Find the magnetic field 50.0 cm from a
straight wire carrying 1200 A from the batteries to the drive
mechanism of a submarine. (b) What is the field if the wires to
and from the drive mechanism are side by side? (c) Discuss
the effects this could have for a compass on the submarine
that is not shielded.
64. How strong is the magnetic field inside a solenoid with
10,000 turns per meter that carries 20.0 A?
65. What current is needed in the solenoid described in
Exercise 22.58 to produce a magnetic field 104
times the
Earth’s magnetic field of 5.00×10−5
T ?
66. How far from the starter cable of a car, carrying 150 A,
must you be to experience a field less than the Earth’s
(5.00×10−5
T)? Assume a long straight wire carries the
current. (In practice, the body of your car shields the
dashboard compass.)
67. Measurements affect the system being measured, such
as the current loop in Figure 22.62. (a) Estimate the field the
loop creates by calculating the field at the center of a circular
loop 20.0 cm in diameter carrying 5.00 A. (b) What is the
smallest field strength this loop can be used to measure, if its
field must alter the measured field by less than 0.0100%?
68. Figure 22.68 shows a long straight wire just touching a
loop carrying a current I1 . Both lie in the same plane. (a)
What direction must the current I2 in the straight wire have
to create a field at the center of the loop in the direction
opposite to that created by the loop? (b) What is the ratio of
I1 / I2 that gives zero field strength at the center of the loop?
(c) What is the direction of the field directly above the loop
under this circumstance?
Figure 22.68
69. Find the magnitude and direction of the magnetic field at
the point equidistant from the wires in Figure 22.64(a), using
the rules of vector addition to sum the contributions from each
wire.
70. Find the magnitude and direction of the magnetic field at
the point equidistant from the wires in Figure 22.64(b), using
the rules of vector addition to sum the contributions from each
wire.
71. What current is needed in the top wire in Figure 22.64(a)
to produce a field of zero at the point equidistant from the
wires, if the currents in the bottom two wires are both 10.0 A
into the page?
72. Calculate the size of the magnetic field 20 m below a high
voltage power line. The line carries 450 MW at a voltage of
300,000 V.
73. Integrated Concepts
(a) A pendulum is set up so that its bob (a thin copper disk)
swings between the poles of a permanent magnet as shown
in Figure 22.69. What is the magnitude and direction of the
magnetic force on the bob at the lowest point in its path, if it
has a positive 0.250 μC charge and is released from a
height of 30.0 cm above its lowest point? The magnetic field
strength is 1.50 T. (b) What is the acceleration of the bob at
the bottom of its swing if its mass is 30.0 grams and it is hung
from a flexible string? Be certain to include a free-body
diagram as part of your analysis.
Figure 22.69
(a) What voltage will accelerate electrons to a speed of
6.00×10−7
m/s ? (b) Find the radius of curvature of the
path of a proton accelerated through this potential in a
0.500-T field and compare this with the radius of curvature of
an electron accelerated through the same potential.
Find the radius of curvature of the path of a 25.0-MeV proton
moving perpendicularly to the 1.20-T field of a cyclotron.
To construct a nonmechanical water meter, a 0.500-T
magnetic field is placed across the supply water pipe to a
home and the Hall voltage is recorded. (a) Find the flow rate
in liters per second through a 3.00-cm-diameter pipe if the
Hall voltage is 60.0 mV. (b) What would the Hall voltage be for
the same flow rate through a 10.0-cm-diameter pipe with the
same field applied?
(a) Using the values given for an MHD drive in Exercise
22.59, and assuming the force is uniformly applied to the
fluid, calculate the pressure created in N/m2
. (b) Is this a
significant fraction of an atmosphere?
(a) Calculate the maximum torque on a 50-turn, 1.50 cm
radius circular current loop carrying 50 μA in a 0.500-T field.
(b) If this coil is to be used in a galvanometer that reads
50 μA full scale, what force constant spring must be used, if
it is attached 1.00 cm from the axis of rotation and is
stretched by the 60º arc moved?

A current balance used to define the ampere is designed so
that the current through it is constant, as is the distance
between wires. Even so, if the wires change length with
temperature, the force between them will change. What
percent change in force per degree will occur if the wires are
copper?
(a) Show that the period of the circular orbit of a charged
particle moving perpendicularly to a uniform magnetic field is
T = 2πm / (qB) . (b) What is the frequency f ? (c) What is
the angular velocity ω ? Note that these results are
independent of the velocity and radius of the orbit and, hence,
of the energy of the particle. (Figure 22.70.)
Figure 22.70 Cyclotrons accelerate charged particles orbiting in a
magnetic field by placing an AC voltage on the metal Dees, between
which the particles move, so that energy is added twice each orbit. The
frequency is constant, since it is independent of the particle energy—the
radius of the orbit simply increases with energy until the particles
approach the edge and are extracted for various experiments and
applications.
A cyclotron accelerates charged particles as shown in Figure
22.70. Using the results of the previous problem, calculate the
frequency of the accelerating voltage needed for a proton in a
1.20-T field.
(a) A 0.140-kg baseball, pitched at 40.0 m/s horizontally and
perpendicular to the Earth’s horizontal 5.00×10−5
T field,
has a 100-nC charge on it. What distance is it deflected from
its path by the magnetic force, after traveling 30.0 m
horizontally? (b) Would you suggest this as a secret
technique for a pitcher to throw curve balls?
(a) What is the direction of the force on a wire carrying a
current due east in a location where the Earth’s field is due
north? Both are parallel to the ground. (b) Calculate the force
per meter if the wire carries 20.0 A and the field strength is
3.00×10−5
T . (c) What diameter copper wire would have
its weight supported by this force? (d) Calculate the
resistance per meter and the voltage per meter needed.
One long straight wire is to be held directly above another by
repulsion between their currents. The lower wire carries 100
A and the wire 7.50 cm above it is 10-gauge (2.588 mm
diameter) copper wire. (a) What current must flow in the
upper wire, neglecting the Earth’s field? (b) What is the
smallest current if the Earth’s 3.00×10−5
T field is parallel
to the ground and is not neglected? (c) Is the supported wire
in a stable or unstable equilibrium if displaced vertically? If
displaced horizontally?
85. Unreasonable Results
(a) Find the charge on a baseball, thrown at 35.0 m/s
perpendicular to the Earth’s 5.00×10−5
T field, that
experiences a 1.00-N magnetic force. (b) What is
unreasonable about this result? (c) Which assumption or
premise is responsible?
A charged particle having mass 6.64×10−27
kg (that of a
helium atom) moving at 8.70×105
m/s perpendicular to a
1.50-T magnetic field travels in a circular path of radius 16.0
mm. (a) What is the charge of the particle? (b) What is
unreasonable about this result? (c) Which assumptions are
responsible?
An inventor wants to generate 120-V power by moving a
1.00-m-long wire perpendicular to the Earth’s 5.00×10−5
T
field. (a) Find the speed with which the wire must move. (b)
What is unreasonable about this result? (c) Which
assumption is responsible?
Frustrated by the small Hall voltage obtained in blood flow
measurements, a medical physicist decides to increase the
applied magnetic field strength to get a 0.500-V output for
blood moving at 30.0 cm/s in a 1.50-cm-diameter vessel. (a)
What magnetic field strength is needed? (b) What is
unreasonable about this result? (c) Which premise is
responsible?
A surveyor 100 m from a long straight 200-kV DC power line
suspects that its magnetic field may equal that of the Earth
and affect compass readings. (a) Calculate the current in the
wire needed to create a 5.00×10−5
T field at this distance.
(b) What is unreasonable about this result? (c) Which
assumption or premise is responsible?
90. Construct Your Own Problem
Consider a mass separator that applies a magnetic field
perpendicular to the velocity of ions and separates the ions
based on the radius of curvature of their paths in the field.
Construct a problem in which you calculate the magnetic field
strength needed to separate two ions that differ in mass, but
not charge, and have the same initial velocity. Among the
things to consider are the types of ions, the velocities they
can be given before entering the magnetic field, and a
reasonable value for the radius of curvature of the paths they
follow. In addition, calculate the separation distance between
the ions at the point where they are detected.
Consider using the torque on a current-carrying coil in a
magnetic field to detect relatively small magnetic fields (less
than the field of the Earth, for example). Construct a problem
in which you calculate the maximum torque on a current-
carrying loop in a magnetic field. Among the things to be

considered are the size of the coil, the number of loops it has,
the current you pass through the coil, and the size of the field
you wish to detect. Discuss whether the torque produced is
large enough to be effectively measured. Your instructor may
also wish for you to consider the effects, if any, of the field
produced by the coil on the surroundings that could affect
detection of the small field.
Test Prep for AP® Courses
1. A bar magnet is oriented so that the north pole of the bar
magnet points north. A compass needle is placed to the north
of the bar magnet. In which direction does the north pole of
the compass needle point?
a. North
b. East
c. South
d. West
2. Assume for simplicity that the Earth’s magnetic north pole
is at the same location as its geographic north pole. If you are
in an airplane flying due west along the equator, as you cross
the prime meridian (0° longitude) facing west and look down
at a compass you are carrying, you see that the compass
needle is perpendicular to your direction of motion, and the
north pole of the needle dipole points to your right. As you
continue flying due west, describe how and why the
orientation of the needle will (or will not) change.
3. Describe how the magnetic domains in an unmagnetized
iron rod will respond to the presence of a strong external
magnetic field.
a. The domains will split into monopoles.
b. The domains will tend to align with the external field.
c. The domains will tend to orient themselves
perpendicular to the external field.
d. The domains will tend to align so as to cancel out the
external field.
4. Describe what steps must be undertaken in order to
convert an unmagnetized iron rod into a permanently
magnetized state. As part of your answer, explain what a
magnetic domain is and how it responds to the steps
described.
5. Iron is ferromagnetic and lead is diamagnetic, which means
its magnetic domains respond in the opposite direction of
ferromagnets but many orders of magnitude more weakly.
The two blocks are placed in a magnetic field that points to
the right. Which of the following best represents the
orientations of the dipoles when the field is present?
Iron Lead
(a)
Figure 22.71 Figure 22.72
(b)
(c)
(d)
6. A weather vane is some sort of directional arrow parallel to
the ground that may rotate freely in a horizontal plane. A
typical weather vane has a large cross-sectional area
perpendicular to the direction the arrow is pointing, like a
“One Way” street sign. The purpose of the weather vane is to
indicate the direction of the wind. As wind blows past the
weather vane, it tends to orient the arrow in the same
direction as the wind. Consider a weather vane’s response to
a strong wind. Explain how this is both similar to and different
from a magnetic domain’s response to an external magnetic
field. How does each affect its surroundings?
22.4 Magnetic Field Strength: Force on a
Moving Charge in a Magnetic Field
7. A proton moves in the –x-direction and encounters a
uniform magnetic field pointing in the +x-direction. In what
direction is the resulting magnetic force on the proton?
a. The proton experiences no magnetic force.
b. +x-direction
c. −y-direction
d. +y-direction
8. A proton moves with a speed of 240 m/s in the +x-direction
into a region of a 4.5-T uniform magnetic field directed 62°
above the +x-direction in the x,y-plane. Calculate the
magnitude of the magnetic force on the proton.
22.5 Force on a Moving Charge in a Magnetic
Field: Examples and Applications
9. A wire oriented north-south carries current south. The wire
is immersed in the Earth’s magnetic field, which is also
oriented north-south (with a horizontal component pointing
north). The Earth’s magnetic field also has a vertical

component pointing down. What is the direction of the
magnetic force felt by the wire?
a. West
b. East
c. Up
d. North
10. An airplane wingspan can be approximated as a
conducting rod of length 35 m. As the airplane flies due north,
it is flying at a rate of 82 m/s through the Earth’s magnetic
field, which has a magnitude of 45 μT toward the north in a
direction 57° below the horizontal plane. (a) Which end of the
wingspan is positively charged, the east or west end?
Explain. (b) What is the Hall emf along the wingspan?
22.9 Magnetic Fields Produced by Currents:
Ampere’s Law
11. An experimentalist fires a beam of electrons, creating a
visible path in the air that can be measured. The beam is fired
along a direction parallel to a current-carrying wire, and the
electrons travel in a circular path in response to the wire’s
magnetic field. Assuming the mass and charge of the
electrons is known, what quantities would you need to
measure in order to deduce the current in the wire?
a. the radius of the circular path
b. the average distance between the electrons and the
wire
c. the velocity of the electrons
d. two of the above
e. all of the above
12. Electrons starting from rest are accelerated through a
potential difference of 240 V and fired into a region of uniform
3.5-mT magnetic field generated by a large solenoid. The
electrons are initially moving in the +x-direction upon entering
the field, and the field is directed into the page. Determine (a)
the radius of the circle in which the electrons will move in this
uniform magnetic field and (b) the initial direction of the
magnetic force the electrons feel upon entering the uniform
field of the solenoid.
13. In terms of the direction of force, we use the left-hand
rule. Pointing your thumb in the +x-direction with the velocity
and fingers of the left hand into the page reveals that the
magnetic force points down toward the bottom of the page in
the –y-direction.
A wire along the y-axis carries current in the +y-direction. In
what direction is the magnetic field at a point on the +x-axis
near the wire?
a. away from the wire
b. vertically upward
c. into the page
d. out of the page
14. Imagine the xy coordinate plane is the plane of the page.
A wire along the z-axis carries current in the +z-direction (out
of the page, or ⊙ ). Draw a diagram of the magnetic field in
the vicinity of this wire indicating the direction of the field.
Also, describe how the strength of the magnetic field varies
according to the distance from the z-axis.
22.10 Magnetic Force between Two Parallel
Conductors
15. Two parallel wires carry equal currents in the same
direction and are separated by a small distance. What is the
direction of the magnetic force exerted by the two wires on
each other?
a. No force since the wires are parallel.
b. No force since the currents are in the same direction.
c. The force is attractive.
d. The force is repulsive.
16. A wire along the y-axis carries current in the +y-direction.
An experimenter would like to arrange a second wire parallel
to the first wire and crossing the x-axis at the coordinate
x = 2.0 m so that the total magnetic field at the coordinate
x = 1.0 m is zero. In what direction must the current flow in
the second wire, assuming it is equal in magnitude to the
current in the first wire? Explain.

23 ELECTROMAGNETIC INDUCTION, AC
CIRCUITS, AND ELECTRICAL
TECHNOLOGIES
Figure 23.1 This wind turbine in the Thames Estuary in the UK is an example of induction at work. Wind pushes the blades of the turbine, spinning a
shaft attached to magnets. The magnets spin around a conductive coil, inducing an electric current in the coil, and eventually feeding the electrical grid.
(credit: phault, Flickr)
Chapter Outline
23.1. Induced Emf and Magnetic Flux
23.2. Faraday’s Law of Induction: Lenz’s Law
23.3. Motional Emf
23.4. Eddy Currents and Magnetic Damping
23.5. Electric Generators
23.6. Back Emf
23.7. Transformers
23.8. Electrical Safety: Systems and Devices
23.9. Inductance
23.10. RL Circuits
23.11. Reactance, Inductive and Capacitive
23.12. RLC Series AC Circuits
Chapter 23 | Electromagnetic Induction, AC Circuits, and Electrical Technologies 1015

Connection for AP® Courses
Nature’s displays of symmetry are beautiful and alluring. As shown in Figure 23.2, a butterfly’s wings exhibit an appealing
symmetry in a complex system. The laws of physics display symmetries at the most basic level – these symmetries are a source
of wonder and imply deeper meaning. Since we place a high value on symmetry, we look for it when we explore nature. The
remarkable thing is that we find it.
Figure 23.2 A butterfly with symmetrically patterned wings is resting on a flower. Physics, like this butterfly, has inherent symmetries. (credit: Thomas
Bresson).
This chapter supports Big Idea 4, illustrating how electric and magnetic changes can take place in a system due to interactions
with other systems. The hint of symmetry between electricity and magnetism found in the preceding chapter will be elaborated
upon in this chapter. Specifically, we know that a current creates a magnetic field. If nature is symmetric in this case, then
perhaps a magnetic field can create a current. Historically, it was very shortly after Oersted discovered that currents cause
magnetic fields that other scientists asked the following question: Can magnetic fields cause currents? The answer was soon
found by experiment to be yes. In 1831, some 12 years after Oersted’s discovery, the English scientist Michael Faraday
(1791–1862) and the American scientist Joseph Henry (1797–1878) independently demonstrated that magnetic fields can
produce currents. The basic process of generating emfs (electromotive forces), and hence currents, with magnetic fields is
known as induction; this process is also called “magnetic induction” to distinguish it from charging by induction, which utilizes the
Coulomb force.
Today, currents induced by magnetic fields are essential to our technological society. The ubiquitous generator – found in
automobiles, on bicycles, in nuclear power plants, and so on – uses magnetism to generate current. Other devices that use
magnetism to induce currents include pickup coils in electric guitars, transformers of every size, certain microphones, airport
security gates, and damping mechanisms on sensitive chemical balances. Explanations and examples in this chapter will help
you understand current induction via magnetic interactions in mechanical systems (Enduring Understanding 4.E, Essential
Knowledge 4.E.2). You will also learn how the behavior of AC circuits depends strongly on the effect of magnetic fields on
currents.
The content of this chapter supports:
Big Idea 4 Interactions between systems can result in changes in those systems.
Enduring Understanding 4.E The electric and magnetic properties of a system can change in response to the presence of, or
changes in, other objects or systems.
Essential Knowledge 4.E.2 Changing magnetic flux induces an electric field that can establish an induced emf in a system.
23.1 Induced Emf and Magnetic Flux
Learning Objectives
• Calculate the flux of a uniform magnetic field through a loop of arbitrary orientation.
• Describe methods to produce an electromotive force (emf) with a magnetic field or a magnet and a loop of wire.
• 4.E.2.1 The student is able to construct an explanation of the function of a simple electromagnetic device in which an
induced emf is produced by a changing magnetic flux through an area defined by a current loop (i.e., a simple
microphone or generator) or of the effect on behavior of a device in which an induced emf is produced by a constant
magnetic field through a changing area. (S.P. 6.4)
The apparatus used by Faraday to demonstrate that magnetic fields can create currents is illustrated in Figure 23.3. When the
switch is closed, a magnetic field is produced in the coil on the top part of the iron ring and transmitted to the coil on the bottom
1016 Chapter 23 | Electromagnetic Induction, AC Circuits, and Electrical Technologies

part of the ring. The galvanometer is used to detect any current induced in the coil on the bottom. It was found that each time the
switch is closed, the galvanometer detects a current in one direction in the coil on the bottom. (You can also observe this in a
physics lab.) Each time the switch is opened, the galvanometer detects a current in the opposite direction. Interestingly, if the
switch remains closed or open for any length of time, there is no current through the galvanometer. Closing and opening the
switch induces the current. It is the change in magnetic field that creates the current. More basic than the current that flows is the
emfthat causes it. The current is a result of an emf induced by a changing magnetic field, whether or not there is a path for
current to flow.
Figure 23.3 Faraday’s apparatus for demonstrating that a magnetic field can produce a current. A change in the field produced by the top coil induces
an emf and, hence, a current in the bottom coil. When the switch is opened and closed, the galvanometer registers currents in opposite directions. No
current flows through the galvanometer when the switch remains closed or open.
An experiment easily performed and often done in physics labs is illustrated in Figure 23.4. An emf is induced in the coil when a
bar magnet is pushed in and out of it. Emfs of opposite signs are produced by motion in opposite directions, and the emfs are
also reversed by reversing poles. The same results are produced if the coil is moved rather than the magnet—it is the relative
motion that is important. The faster the motion, the greater the emf, and there is no emf when the magnet is stationary relative to
the coil.
Figure 23.4 Movement of a magnet relative to a coil produces emfs as shown. The same emfs are produced if the coil is moved relative to the magnet.
The greater the speed, the greater the magnitude of the emf, and the emf is zero when there is no motion.
The method of inducing an emf used in most electric generators is shown in Figure 23.5. A coil is rotated in a magnetic field,
producing an alternating current emf, which depends on rotation rate and other factors that will be explored in later sections.
Note that the generator is remarkably similar in construction to a motor (another symmetry).

Figure 23.5 Rotation of a coil in a magnetic field produces an emf. This is the basic construction of a generator, where work done to turn the coil is
converted to electric energy. Note the generator is very similar in construction to a motor.
So we see that changing the magnitude or direction of a magnetic field produces an emf. Experiments revealed that there is a
crucial quantity called the magnetic flux, Φ , given by
(23.1)Φ = BA cos θ,
where B is the magnetic field strength over an area A , at an angle θ with the perpendicular to the area as shown in Figure
23.6. Any change in magnetic flux Φ induces an emf. This process is defined to be electromagnetic induction. Units of
magnetic flux Φ are T ⋅ m2
. As seen in Figure 23.6, B cos θ = B ⊥, which is the component of B perpendicular to the area
A . Thus magnetic flux is Φ = B⊥A , the product of the area and the component of the magnetic field perpendicular to it.
Figure 23.6 Magnetic flux Φ is related to the magnetic field and the area over which it exists. The flux Φ = BA cos θ is related to induction; any
change in Φ induces an emf.
All induction, including the examples given so far, arises from some change in magnetic flux Φ . For example, Faraday changed
B and hence Φ when opening and closing the switch in his apparatus (shown in Figure 23.3). This is also true for the bar
magnet and coil shown in Figure 23.4. When rotating the coil of a generator, the angle θ and, hence, Φ is changed. Just how
great an emf and what direction it takes depend on the change in Φ and how rapidly the change is made, as examined in the
next section.

23.2 Faraday’s Law of Induction: Lenz’s Law
Learning Objectives
• Calculate emf, current, and magnetic fields using Faraday’s law.
• Explain the physical results of Lenz’s law.
Faraday’s and Lenz’s Law
Faraday’s experiments showed that the emf induced by a change in magnetic flux depends on only a few factors. First, emf is
directly proportional to the change in flux ΔΦ . Second, emf is greatest when the change in time Δt is smallest—that is, emf is
inversely proportional to Δt . Finally, if a coil has N turns, an emf will be produced that is N times greater than for a single coil,
so that emf is directly proportional to N . The equation for the emf induced by a change in magnetic flux is
(23.2)
emf = −NΔΦ
Δt
.
This relationship is known as Faraday’s law of induction. The units for emf are volts, as is usual.
The minus sign in Faraday’s law of induction is very important. The minus means that the emf creates a current I and magnetic
field B that oppose the change in flux ΔΦ —this is known as Lenz’s law. The direction (given by the minus sign) of the emfis so
important that it is called Lenz’s law after the Russian Heinrich Lenz (1804–1865), who, like Faraday and Henry,independently
investigated aspects of induction. Faraday was aware of the direction, but Lenz stated it so clearly that he is credited for its
discovery. (See Figure 23.7.)
Figure 23.7 (a) When this bar magnet is thrust into the coil, the strength of the magnetic field increases in the coil. The current induced in the coil
creates another field, in the opposite direction of the bar magnet’s to oppose the increase. This is one aspect of Lenz’s law—induction opposes any
change in flux. (b) and (c) are two other situations. Verify for yourself that the direction of the induced Bcoil shown indeed opposes the change in flux
and that the current direction shown is consistent with RHR-2.
Problem-Solving Strategy for Lenz’s Law
To use Lenz’s law to determine the directions of the induced magnetic fields, currents, and emfs:
1. Make a sketch of the situation for use in visualizing and recording directions.
2. Determine the direction of the magnetic field B.
3. Determine whether the flux is increasing or decreasing.
4. Now determine the direction of the induced magnetic field B. It opposes the change in flux by adding or subtracting
from the original field.
5. Use RHR-2 to determine the direction of the induced current I that is responsible for the induced magnetic field B.

6. The direction (or polarity) of the induced emf will now drive a current in this direction and can be represented as current
emerging from the positive terminal of the emf and returning to its negative terminal.
For practice, apply these steps to the situations shown in Figure 23.7 and to others that are part of the following text material.
Applications of Electromagnetic Induction
There are many applications of Faraday’s Law of induction, as we will explore in this chapter and others. At this juncture, let us
mention several that have to do with data storage and magnetic fields. A very important application has to do with audio and
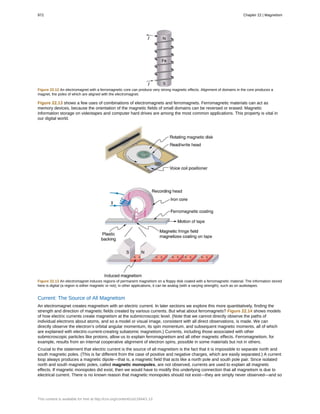
video recording tapes. A plastic tape, coated with iron oxide, moves past a recording head. This recording head is basically a
round iron ring about which is wrapped a coil of wire—an electromagnet (Figure 23.8). A signal in the form of a varying input
current from a microphone or camera goes to the recording head. These signals (which are a function of the signal amplitude
and frequency) produce varying magnetic fields at the recording head. As the tape moves past the recording head, the magnetic
field orientations of the iron oxide molecules on the tape are changed thus recording the signal. In the playback mode, the
magnetized tape is run past another head, similar in structure to the recording head. The different magnetic field orientations of
the iron oxide molecules on the tape induces an emf in the coil of wire in the playback head. This signal then is sent to a
loudspeaker or video player.
Figure 23.8 Recording and playback heads used with audio and video magnetic tapes. (credit: Steve Jurvetson)
Similar principles apply to computer hard drives, except at a much faster rate. Here recordings are on a coated, spinning disk.
Read heads historically were made to work on the principle of induction. However, the input information is carried in digital rather
than analog form – a series of 0’s or 1’s are written upon the spinning hard drive. Today, most hard drive readout devices do not
work on the principle of induction, but use a technique known as giant magnetoresistance. (The discovery that weak changes in
a magnetic field in a thin film of iron and chromium could bring about much larger changes in electrical resistance was one of the
first large successes of nanotechnology.) Another application of induction is found on the magnetic stripe on the back of your
personal credit card as used at the grocery store or the ATM machine. This works on the same principle as the audio or video
tape mentioned in the last paragraph in which a head reads personal information from your card.
Another application of electromagnetic induction is when electrical signals need to be transmitted across a barrier. Consider the
cochlear implant shown below. Sound is picked up by a microphone on the outside of the skull and is used to set up a varying
magnetic field. A current is induced in a receiver secured in the bone beneath the skin and transmitted to electrodes in the inner
ear. Electromagnetic induction can be used in other instances where electric signals need to be conveyed across various media.
Figure 23.9 Electromagnetic induction used in transmitting electric currents across mediums. The device on the baby’s head induces an electrical
current in a receiver secured in the bone beneath the skin. (credit: Bjorn Knetsch)
Another contemporary area of research in which electromagnetic induction is being successfully implemented (and with
substantial potential) is transcranial magnetic simulation. A host of disorders, including depression and hallucinations can be
traced to irregular localized electrical activity in the brain. In transcranial magnetic stimulation, a rapidly varying and very
localized magnetic field is placed close to certain sites identified in the brain. Weak electric currents are induced in the identified
sites and can result in recovery of electrical functioning in the brain tissue.
Sleep apnea (“the cessation of breath”) affects both adults and infants (especially premature babies and it may be a cause of
sudden infant deaths [SID]). In such individuals, breath can stop repeatedly during their sleep. A cessation of more than 20
seconds can be very dangerous. Stroke, heart failure, and tiredness are just some of the possible consequences for a person
having sleep apnea. The concern in infants is the stopping of breath for these longer times. One type of monitor to alert parents
when a child is not breathing uses electromagnetic induction. A wire wrapped around the infant’s chest has an alternating current
running through it. The expansion and contraction of the infant’s chest as the infant breathes changes the area through the coil.
A pickup coil located nearby has an alternating current induced in it due to the changing magnetic field of the initial wire. If the
child stops breathing, there will be a change in the induced current, and so a parent can be alerted.

Making Connections: Conservation of Energy
Lenz’s law is a manifestation of the conservation of energy. The induced emf produces a current that opposes the change in
flux, because a change in flux means a change in energy. Energy can enter or leave, but not instantaneously. Lenz’s law is a
consequence. As the change begins, the law says induction opposes and, thus, slows the change. In fact, if the induced emf
were in the same direction as the change in flux, there would be a positive feedback that would give us free energy from no
apparent source—conservation of energy would be violated.
Example 23.1 Calculating Emf: How Great Is the Induced Emf?
Calculate the magnitude of the induced emf when the magnet in Figure 23.7(a) is thrust into the coil, given the following
information: the single loop coil has a radius of 6.00 cm and the average value of B cos θ (this is given, since the bar
magnet’s field is complex) increases from 0.0500 T to 0.250 T in 0.100 s.
Strategy
To find the magnitude of emf, we use Faraday’s law of induction as stated by emf = −NΔΦ
Δt
, but without the minus sign
that indicates direction:
(23.3)
emf = NΔΦ
Δt
.
Solution
We are given that N = 1 and Δt = 0.100 s , but we must determine the change in flux ΔΦ before we can find emf.
Since the area of the loop is fixed, we see that
(23.4)ΔΦ = Δ(BA cos θ) = AΔ(B cos θ).
Now Δ(B cos θ) = 0.200 T , since it was given that B cos θ changes from 0.0500 to 0.250 T. The area of the loop is
A = πr2
= (3.14...)(0.060 m)2
= 1.13×10−2
m2
. Thus,
(23.5)ΔΦ = (1.13×10−2
m2
)(0.200 T).
Entering the determined values into the expression for emf gives
(23.6)
Emf = NΔΦ
Δt
=
(1.13×10−2
m2
)(0.200 T)
0.100 s
= 22.6 mV.
Discussion
While this is an easily measured voltage, it is certainly not large enough for most practical applications. More loops in the
coil, a stronger magnet, and faster movement make induction the practical source of voltages that it is.
PhET Explorations: Faraday's Electromagnetic Lab
Play with a bar magnet and coils to learn about Faraday's law. Move a bar magnet near one or two coils to make a light bulb
glow. View the magnetic field lines. A meter shows the direction and magnitude of the current. View the magnetic field lines
or use a meter to show the direction and magnitude of the current. You can also play with electromagnets, generators and
transformers!
Figure 23.10 Faraday's Electromagnetic Lab (http://cnx.org/content/m55407/1.2/faraday_en.jar)
23.3 Motional Emf
Learning Objectives
• Calculate emf, force, magnetic field, and work due to the motion of an object in a magnetic field.

As we have seen, any change in magnetic flux induces an emf opposing that change—a process known as induction. Motion is
one of the major causes of induction. For example, a magnet moved toward a coil induces an emf, and a coil moved toward a
magnet produces a similar emf. In this section, we concentrate on motion in a magnetic field that is stationary relative to the
Earth, producing what is loosely called motional emf.
One situation where motional emf occurs is known as the Hall effect and has already been examined. Charges moving in a
magnetic field experience the magnetic force F = qvB sin θ , which moves opposite charges in opposite directions and
produces an emf = Bℓv . We saw that the Hall effect has applications, including measurements of B and v . We will now see
that the Hall effect is one aspect of the broader phenomenon of induction, and we will find that motional emf can be used as a
power source.
Consider the situation shown in Figure 23.11. A rod is moved at a speed v along a pair of conducting rails separated by a
distance ℓ in a uniform magnetic field B . The rails are stationary relative to B and are connected to a stationary resistor R .
The resistor could be anything from a light bulb to a voltmeter. Consider the area enclosed by the moving rod, rails, and resistor.
B is perpendicular to this area, and the area is increasing as the rod moves. Thus the magnetic flux enclosed by the rails, rod,
and resistor is increasing. When flux changes, an emf is induced according to Faraday’s law of induction.
Figure 23.11 (a) A motional emf = Bℓv is induced between the rails when this rod moves to the right in the uniform magnetic field. The magnetic
field B is into the page, perpendicular to the moving rod and rails and, hence, to the area enclosed by them. (b) Lenz’s law gives the directions of the
induced field and current, and the polarity of the induced emf. Since the flux is increasing, the induced field is in the opposite direction, or out of the
page. RHR-2 gives the current direction shown, and the polarity of the rod will drive such a current. RHR-1 also indicates the same polarity for the rod.
(Note that the script E symbol used in the equivalent circuit at the bottom of part (b) represents emf.)
To find the magnitude of emf induced along the moving rod, we use Faraday’s law of induction without the sign:
(23.7)
emf = NΔΦ
Δt
.

Here and below, “emf” implies the magnitude of the emf. In this equation, N = 1 and the flux Φ = BA cos θ . We have
θ = 0º and cos θ = 1 , since B is perpendicular to A . Now ΔΦ = Δ(BA) = BΔA , since B is uniform. Note that the area
swept out by the rod is ΔA = ℓ Δ x . Entering these quantities into the expression for emf yields
(23.8)
emf = BΔA
Δt
= BℓΔx
Δt
.
Finally, note that Δx / Δt = v , the velocity of the rod. Entering this into the last expression shows that
(23.9)emf = Bℓv (B, l, and v perpendicular)
is the motional emf. This is the same expression given for the Hall effect previously.
Making Connections: Unification of Forces
There are many connections between the electric force and the magnetic force. The fact that a moving electric field
produces a magnetic field and, conversely, a moving magnetic field produces an electric field is part of why electric and
magnetic forces are now considered to be different manifestations of the same force. This classic unification of electric and
magnetic forces into what is called the electromagnetic force is the inspiration for contemporary efforts to unify other basic
forces.
To find the direction of the induced field, the direction of the current, and the polarity of the induced emf, we apply Lenz’s law as
explained in Faraday's Law of Induction: Lenz's Law. (See Figure 23.11(b).) Flux is increasing, since the area enclosed is
increasing. Thus the induced field must oppose the existing one and be out of the page. And so the RHR-2 requires that I be
counterclockwise, which in turn means the top of the rod is positive as shown.
Motional emf also occurs if the magnetic field moves and the rod (or other object) is stationary relative to the Earth (or some
observer). We have seen an example of this in the situation where a moving magnet induces an emf in a stationary coil. It is the
relative motion that is important. What is emerging in these observations is a connection between magnetic and electric fields. A
moving magnetic field produces an electric field through its induced emf. We already have seen that a moving electric field
produces a magnetic field—moving charge implies moving electric field and moving charge produces a magnetic field.
Motional emfs in the Earth’s weak magnetic field are not ordinarily very large, or we would notice voltage along metal rods, such
as a screwdriver, during ordinary motions. For example, a simple calculation of the motional emf of a 1 m rod moving at 3.0 m/s
perpendicular to the Earth’s field gives emf = Bℓv = (5.0×10−5
T)(1.0 m)(3.0 m/s) = 150 μV . This small value is
consistent with experience. There is a spectacular exception, however. In 1992 and 1996, attempts were made with the space
shuttle to create large motional emfs. The Tethered Satellite was to be let out on a 20 km length of wire as shown in Figure
23.12, to create a 5 kV emf by moving at orbital speed through the Earth’s field. This emf could be used to convert some of the
shuttle’s kinetic and potential energy into electrical energy if a complete circuit could be made. To complete the circuit, the
stationary ionosphere was to supply a return path for the current to flow. (The ionosphere is the rarefied and partially ionized
atmosphere at orbital altitudes. It conducts because of the ionization. The ionosphere serves the same function as the stationary
rails and connecting resistor in Figure 23.11, without which there would not be a complete circuit.) Drag on the current in the
cable due to the magnetic force F = IℓB sin θ does the work that reduces the shuttle’s kinetic and potential energy and allows
it to be converted to electrical energy. The tests were both unsuccessful. In the first, the cable hung up and could only be
extended a couple of hundred meters; in the second, the cable broke when almost fully extended. Example 23.2 indicates
feasibility in principle.

Example 23.2 Calculating the Large Motional Emf of an Object in Orbit
Figure 23.12 Motional emf as electrical power conversion for the space shuttle is the motivation for the Tethered Satellite experiment. A 5 kV emf
was predicted to be induced in the 20 km long tether while moving at orbital speed in the Earth’s magnetic field. The circuit is completed by a
return path through the stationary ionosphere.
Calculate the motional emf induced along a 20.0 km long conductor moving at an orbital speed of 7.80 km/s perpendicular to
the Earth’s 5.00×10−5
T magnetic field.
Strategy
This is a straightforward application of the expression for motional emf— emf = Bℓv .
Solution
Entering the given values into emf = Bℓv gives
(23.10)emf = Bℓv
= (5.00×10−5
T)(2.0×104
m)(7.80×103
m/s)
= 7.80×103
V.
Discussion
The value obtained is greater than the 5 kV measured voltage for the shuttle experiment, since the actual orbital motion of
the tether is not perpendicular to the Earth’s field. The 7.80 kV value is the maximum emf obtained when θ = 90º and
sin θ = 1 .
23.4 Eddy Currents and Magnetic Damping
Learning Objectives
• Explain the magnitude and direction of an induced eddy current, and the effect this will have on the object it is induced
in.
• Describe several applications of magnetic damping.
Eddy Currents and Magnetic Damping
As discussed in Motional Emf, motional emf is induced when a conductor moves in a magnetic field or when a magnetic field
moves relative to a conductor. If motional emf can cause a current loop in the conductor, we refer to that current as an eddy
current. Eddy currents can produce significant drag, called magnetic damping, on the motion involved. Consider the apparatus
shown in Figure 23.13, which swings a pendulum bob between the poles of a strong magnet. (This is another favorite physics
lab activity.) If the bob is metal, there is significant drag on the bob as it enters and leaves the field, quickly damping the motion.
If, however, the bob is a slotted metal plate, as shown in Figure 23.13(b), there is a much smaller effect due to the magnet.

There is no discernible effect on a bob made of an insulator. Why is there drag in both directions, and are there any uses for
magnetic drag?
Figure 23.13 A common physics demonstration device for exploring eddy currents and magnetic damping. (a) The motion of a metal pendulum bob
swinging between the poles of a magnet is quickly damped by the action of eddy currents. (b) There is little effect on the motion of a slotted metal bob,
implying that eddy currents are made less effective. (c) There is also no magnetic damping on a nonconducting bob, since the eddy currents are
extremely small.
Figure 23.14 shows what happens to the metal plate as it enters and leaves the magnetic field. In both cases, it experiences a
force opposing its motion. As it enters from the left, flux increases, and so an eddy current is set up (Faraday’s law) in the
counterclockwise direction (Lenz’s law), as shown. Only the right-hand side of the current loop is in the field, so that there is an
unopposed force on it to the left (RHR-1). When the metal plate is completely inside the field, there is no eddy current if the field
is uniform, since the flux remains constant in this region. But when the plate leaves the field on the right, flux decreases, causing
an eddy current in the clockwise direction that, again, experiences a force to the left, further slowing the motion. A similar
analysis of what happens when the plate swings from the right toward the left shows that its motion is also damped when
entering and leaving the field.
Figure 23.14 A more detailed look at the conducting plate passing between the poles of a magnet. As it enters and leaves the field, the change in flux
produces an eddy current. Magnetic force on the current loop opposes the motion. There is no current and no magnetic drag when the plate is
completely inside the uniform field.
When a slotted metal plate enters the field, as shown in Figure 23.15, an emf is induced by the change in flux, but it is less
effective because the slots limit the size of the current loops. Moreover, adjacent loops have currents in opposite directions, and
their effects cancel. When an insulating material is used, the eddy current is extremely small, and so magnetic damping on
insulators is negligible. If eddy currents are to be avoided in conductors, then they can be slotted or constructed of thin layers of
conducting material separated by insulating sheets.

Figure 23.15 Eddy currents induced in a slotted metal plate entering a magnetic field form small loops, and the forces on them tend to cancel, thereby
making magnetic drag almost zero.
Applications of Magnetic Damping
One use of magnetic damping is found in sensitive laboratory balances. To have maximum sensitivity and accuracy, the balance
must be as friction-free as possible. But if it is friction-free, then it will oscillate for a very long time. Magnetic damping is a simple
and ideal solution. With magnetic damping, drag is proportional to speed and becomes zero at zero velocity. Thus the oscillations
are quickly damped, after which the damping force disappears, allowing the balance to be very sensitive. (See Figure 23.16.) In
most balances, magnetic damping is accomplished with a conducting disc that rotates in a fixed field.
Figure 23.16 Magnetic damping of this sensitive balance slows its oscillations. Since Faraday’s law of induction gives the greatest effect for the most
rapid change, damping is greatest for large oscillations and goes to zero as the motion stops.
Since eddy currents and magnetic damping occur only in conductors, recycling centers can use magnets to separate metals from
other materials. Trash is dumped in batches down a ramp, beneath which lies a powerful magnet. Conductors in the trash are
slowed by magnetic damping while nonmetals in the trash move on, separating from the metals. (See Figure 23.17.) This works
for all metals, not just ferromagnetic ones. A magnet can separate out the ferromagnetic materials alone by acting on stationary
trash.

Figure 23.17 Metals can be separated from other trash by magnetic drag. Eddy currents and magnetic drag are created in the metals sent down this
ramp by the powerful magnet beneath it. Nonmetals move on.
Other major applications of eddy currents are in metal detectors and braking systems in trains and roller coasters. Portable metal
detectors (Figure 23.18) consist of a primary coil carrying an alternating current and a secondary coil in which a current is
induced. An eddy current will be induced in a piece of metal close to the detector which will cause a change in the induced
current within the secondary coil, leading to some sort of signal like a shrill noise. Braking using eddy currents is safer because
factors such as rain do not affect the braking and the braking is smoother. However, eddy currents cannot bring the motion to a
complete stop, since the force produced decreases with speed. Thus, speed can be reduced from say 20 m/s to 5 m/s, but
another form of braking is needed to completely stop the vehicle. Generally, powerful rare earth magnets such as neodymium
magnets are used in roller coasters. Figure 23.19 shows rows of magnets in such an application. The vehicle has metal fins
(normally containing copper) which pass through the magnetic field slowing the vehicle down in much the same way as with the
pendulum bob shown in Figure 23.13.
Figure 23.18 A soldier in Iraq uses a metal detector to search for explosives and weapons. (credit: U.S. Army)
Figure 23.19 The rows of rare earth magnets (protruding horizontally) are used for magnetic braking in roller coasters. (credit: Stefan Scheer,
Wikimedia Commons)

Induction cooktops have electromagnets under their surface. The magnetic field is varied rapidly producing eddy currents in the
base of the pot, causing the pot and its contents to increase in temperature. Induction cooktops have high efficiencies and good
response times but the base of the pot needs to be ferromagnetic, iron or steel for induction to work.
23.5 Electric Generators
Learning Objectives
• Calculate the emf induced in a generator.
• Calculate the peak emf that can be induced in a particular generator system.
magnetic field through a changing area. (SP.6.4)
Electric generators induce an emf by rotating a coil in a magnetic field, as briefly discussed in Induced Emf and Magnetic
Flux. We will now explore generators in more detail. Consider the following example.
Example 23.3 Calculating the Emf Induced in a Generator Coil
The generator coil shown in Figure 23.20 is rotated through one-fourth of a revolution (from θ = 0º to θ = 90º ) in 15.0
ms. The 200-turn circular coil has a 5.00 cm radius and is in a uniform 1.25 T magnetic field. What is the average emf
induced?
Figure 23.20 When this generator coil is rotated through one-fourth of a revolution, the magnetic flux Φ changes from its maximum to zero,
inducing an emf.
Strategy
We use Faraday’s law of induction to find the average emf induced over a time Δt :
(23.11)
emf = −NΔΦ
Δt
.
We know that N = 200 and Δt = 15.0 ms , and so we must determine the change in flux ΔΦ to find emf.
Solution

Since the area of the loop and the magnetic field strength are constant, we see that
(23.12)ΔΦ = Δ(BA cos θ) = ABΔ(cos θ).
Now, Δ(cos θ) = −1.0 , since it was given that θ goes from 0º to 90º . Thus ΔΦ = −AB , and
(23.13)
emf = N AB
Δt
.
The area of the loop is A = πr2
= (3.14...)(0.0500 m)2
= 7.85×10−3
m2
. Entering this value gives
(23.14)
emf = 200
(7.85×10−3
m2
)(1.25 T)
15.0×10−3
s
= 131 V.
Discussion
This is a practical average value, similar to the 120 V used in household power.
The emf calculated in Example 23.3 is the average over one-fourth of a revolution. What is the emf at any given instant? It varies
with the angle between the magnetic field and a perpendicular to the coil. We can get an expression for emf as a function of time
by considering the motional emf on a rotating rectangular coil of width w and height ℓ in a uniform magnetic field, as illustrated
in Figure 23.21.
Figure 23.21 A generator with a single rectangular coil rotated at constant angular velocity in a uniform magnetic field produces an emf that varies
sinusoidally in time. Note the generator is similar to a motor, except the shaft is rotated to produce a current rather than the other way around.
Charges in the wires of the loop experience the magnetic force, because they are moving in a magnetic field. Charges in the
vertical wires experience forces parallel to the wire, causing currents. But those in the top and bottom segments feel a force
perpendicular to the wire, which does not cause a current. We can thus find the induced emf by considering only the side wires.
Motional emf is given to be emf = Bℓv , where the velocity v is perpendicular to the magnetic field B . Here the velocity is at an
angle θ with B , so that its component perpendicular to B is v sin θ (see Figure 23.21). Thus in this case the emf induced on
each side is emf = Bℓv sin θ , and they are in the same direction. The total emf around the loop is then
(23.15)emf = 2Bℓv sin θ.
This expression is valid, but it does not give emf as a function of time. To find the time dependence of emf, we assume the coil
rotates at a constant angular velocity ω . The angle θ is related to angular velocity by θ = ωt , so that
(23.16)emf = 2Bℓv sin ωt.
Now, linear velocity v is related to angular velocity ω by v = rω . Here r = w / 2 , so that v = (w / 2)ω , and
(23.17)emf = 2Bℓw
2
ω sin ωt = (ℓw)Bω sin ωt.
Noting that the area of the loop is A = ℓw , and allowing for N loops, we find that
(23.18)emf = NABω sin ωt
is the emf induced in a generator coil of N turns and area A rotating at a constant angular velocity ω in a uniform magnetic
field B . This can also be expressed as
(23.19)emf = emf0 sin ωt,
where

(23.20)emf0 = NABω
is the maximum (peak) emf. Note that the frequency of the oscillation is f = ω / 2π , and the period is T = 1 / f = 2π / ω .
Figure 23.22 shows a graph of emf as a function of time, and it now seems reasonable that AC voltage is sinusoidal.
Figure 23.22 The emf of a generator is sent to a light bulb with the system of rings and brushes shown. The graph gives the emf of the generator as a
function of time. emf0 is the peak emf. The period is T = 1 / f = 2π / ω , where f is the frequency. Note that the script E stands for emf.
The fact that the peak emf, emf0 = NABω , makes good sense. The greater the number of coils, the larger their area, and the
stronger the field, the greater the output voltage. It is interesting that the faster the generator is spun (greater ω ), the greater the
emf. This is noticeable on bicycle generators—at least the cheaper varieties. One of the authors as a juvenile found it amusing to
ride his bicycle fast enough to burn out his lights, until he had to ride home lightless one dark night.
Figure 23.23 shows a scheme by which a generator can be made to produce pulsed DC. More elaborate arrangements of
multiple coils and split rings can produce smoother DC, although electronic rather than mechanical means are usually used to
make ripple-free DC.
Figure 23.23 Split rings, called commutators, produce a pulsed DC emf output in this configuration.
Example 23.4 Calculating the Maximum Emf of a Generator
Calculate the maximum emf, emf0 , of the generator that was the subject of Example 23.3.
Strategy
Once ω , the angular velocity, is determined, emf0 = NABω can be used to find emf0 . All other quantities are known.

Solution
Angular velocity is defined to be the change in angle per unit time:
(23.21)
ω = Δθ
Δt
.
One-fourth of a revolution is π/2 radians, and the time is 0.0150 s; thus,
(23.22)
ω = π / 2 rad
0.0150 s
= 104.7 rad/s.
104.7 rad/s is exactly 1000 rpm. We substitute this value for ω and the information from the previous example into
emf0 = NABω , yielding
(23.23)emf0 = NABω
= 200(7.85×10−3
m2
)(1.25 T)(104.7 rad/s)
= 206 V
.
Discussion
The maximum emf is greater than the average emf of 131 V found in the previous example, as it should be.
In real life, electric generators look a lot different than the figures in this section, but the principles are the same. The source of
mechanical energy that turns the coil can be falling water (hydropower), steam produced by the burning of fossil fuels, or the
kinetic energy of wind. Figure 23.24 shows a cutaway view of a steam turbine; steam moves over the blades connected to the
shaft, which rotates the coil within the generator.
Figure 23.24 Steam turbine/generator. The steam produced by burning coal impacts the turbine blades, turning the shaft which is connected to the
generator. (credit: Nabonaco, Wikimedia Commons)
Generators illustrated in this section look very much like the motors illustrated previously. This is not coincidental. In fact, a motor
becomes a generator when its shaft rotates. Certain early automobiles used their starter motor as a generator. In Back Emf, we
shall further explore the action of a motor as a generator.
23.6 Back Emf
Learning Objectives
• Explain what back emf is and how it is induced.
It has been noted that motors and generators are very similar. Generators convert mechanical energy into electrical energy,
whereas motors convert electrical energy into mechanical energy. Furthermore, motors and generators have the same
construction. When the coil of a motor is turned, magnetic flux changes, and an emf (consistent with Faraday’s law of induction)
is induced. The motor thus acts as a generator whenever its coil rotates. This will happen whether the shaft is turned by an
external input, like a belt drive, or by the action of the motor itself. That is, when a motor is doing work and its shaft is turning, an
emf is generated. Lenz’s law tells us the emf opposes any change, so that the input emf that powers the motor will be opposed
by the motor’s self-generated emf, called the back emf of the motor. (See Figure 23.25.)

Figure 23.25 The coil of a DC motor is represented as a resistor in this schematic. The back emf is represented as a variable emf that opposes the
one driving the motor. Back emf is zero when the motor is not turning, and it increases proportionally to the motor’s angular velocity.
Back emf is the generator output of a motor, and so it is proportional to the motor’s angular velocity ω . It is zero when the motor
is first turned on, meaning that the coil receives the full driving voltage and the motor draws maximum current when it is on but
not turning. As the motor turns faster and faster, the back emf grows, always opposing the driving emf, and reduces the voltage
across the coil and the amount of current it draws. This effect is noticeable in a number of situations. When a vacuum cleaner,
refrigerator, or washing machine is first turned on, lights in the same circuit dim briefly due to the IR drop produced in feeder
lines by the large current drawn by the motor. When a motor first comes on, it draws more current than when it runs at its normal
operating speed. When a mechanical load is placed on the motor, like an electric wheelchair going up a hill, the motor slows, the
back emf drops, more current flows, and more work can be done. If the motor runs at too low a speed, the larger current can
overheat it (via resistive power in the coil, P = I2
R ), perhaps even burning it out. On the other hand, if there is no mechanical
load on the motor, it will increase its angular velocity ω until the back emf is nearly equal to the driving emf. Then the motor
uses only enough energy to overcome friction.
Consider, for example, the motor coils represented in Figure 23.25. The coils have a 0.400 Ω equivalent resistance and are
driven by a 48.0 V emf. Shortly after being turned on, they draw a current I = V/R = (48.0 V)/(0.400 Ω ) = 120 A and,
thus, dissipate P = I2
R = 5.76 kW of energy as heat transfer. Under normal operating conditions for this motor, suppose the
back emf is 40.0 V. Then at operating speed, the total voltage across the coils is 8.0 V (48.0 V minus the 40.0 V back emf), and
the current drawn is I = V/R = (8.0 V)/(0.400 Ω ) = 20 A . Under normal load, then, the power dissipated is
P = IV = (20 A) / (8.0 V) = 160 W . The latter will not cause a problem for this motor, whereas the former 5.76 kW would
burn out the coils if sustained.
23.7 Transformers
Learning Objectives
• Explain how a transformer works.
• Calculate voltage, current, and/or number of turns given the other quantities.
Transformers do what their name implies—they transform voltages from one value to another (The term voltage is used rather
than emf, because transformers have internal resistance). For example, many cell phones, laptops, video games, and power
tools and small appliances have a transformer built into their plug-in unit (like that in Figure 23.26) that changes 120 V or 240 V
AC into whatever voltage the device uses. Transformers are also used at several points in the power distribution systems, such
as illustrated in Figure 23.27. Power is sent long distances at high voltages, because less current is required for a given amount
of power, and this means less line loss, as was discussed previously. But high voltages pose greater hazards, so that
transformers are employed to produce lower voltage at the user’s location.

Figure 23.26 The plug-in transformer has become increasingly familiar with the proliferation of electronic devices that operate on voltages other than
common 120 V AC. Most are in the 3 to 12 V range. (credit: Shop Xtreme)
Figure 23.27 Transformers change voltages at several points in a power distribution system. Electric power is usually generated at greater than 10 kV,
and transmitted long distances at voltages over 200 kV—sometimes as great as 700 kV—to limit energy losses. Local power distribution to
neighborhoods or industries goes through a substation and is sent short distances at voltages ranging from 5 to 13 kV. This is reduced to 120, 240, or
480 V for safety at the individual user site.
The type of transformer considered in this text—see Figure 23.28—is based on Faraday’s law of induction and is very similar in
construction to the apparatus Faraday used to demonstrate magnetic fields could cause currents. The two coils are called the
primary and secondary coils. In normal use, the input voltage is placed on the primary, and the secondary produces the
transformed output voltage. Not only does the iron core trap the magnetic field created by the primary coil, its magnetization
increases the field strength. Since the input voltage is AC, a time-varying magnetic flux is sent to the secondary, inducing its AC
output voltage.
Figure 23.28 A typical construction of a simple transformer has two coils wound on a ferromagnetic core that is laminated to minimize eddy currents.
The magnetic field created by the primary is mostly confined to and increased by the core, which transmits it to the secondary coil. Any change in
current in the primary induces a current in the secondary.

For the simple transformer shown in Figure 23.28, the output voltage Vs depends almost entirely on the input voltage Vp and
the ratio of the number of loops in the primary and secondary coils. Faraday’s law of induction for the secondary coil gives its
induced output voltage Vs to be
(23.24)
Vs = −Ns
ΔΦ
Δt
,
where Ns is the number of loops in the secondary coil and ΔΦ / Δt is the rate of change of magnetic flux. Note that the output
voltage equals the induced emf ( Vs = emfs ), provided coil resistance is small (a reasonable assumption for transformers). The
cross-sectional area of the coils is the same on either side, as is the magnetic field strength, and so ΔΦ / Δt is the same on
either side. The input primary voltage Vp is also related to changing flux by
(23.25)
Vp = −Np
ΔΦ
Δt
.
The reason for this is a little more subtle. Lenz’s law tells us that the primary coil opposes the change in flux caused by the input
voltage Vp , hence the minus sign (This is an example of self-inductance, a topic to be explored in some detail in later sections).
Assuming negligible coil resistance, Kirchhoff’s loop rule tells us that the induced emf exactly equals the input voltage. Taking the
ratio of these last two equations yields a useful relationship:
(23.26)Vs
Vp
=
Ns
Np
.
This is known as the transformer equation, and it simply states that the ratio of the secondary to primary voltages in a
transformer equals the ratio of the number of loops in their coils.
The output voltage of a transformer can be less than, greater than, or equal to the input voltage, depending on the ratio of the
number of loops in their coils. Some transformers even provide a variable output by allowing connection to be made at different
points on the secondary coil. A step-up transformer is one that increases voltage, whereas a step-down transformer
decreases voltage. Assuming, as we have, that resistance is negligible, the electrical power output of a transformer equals its
input. This is nearly true in practice—transformer efficiency often exceeds 99%. Equating the power input and output,
(23.27)Pp = IpVp = IsVs = Ps.
Rearranging terms gives
(23.28)Vs
Vp
=
Ip
Is
.
Combining this with
Vs
Vp
=
Ns
Np
, we find that
(23.29)Is
Ip
=
Np
Ns
is the relationship between the output and input currents of a transformer. So if voltage increases, current decreases. Conversely,
if voltage decreases, current increases.
Example 23.5 Calculating Characteristics of a Step-Up Transformer
A portable x-ray unit has a step-up transformer, the 120 V input of which is transformed to the 100 kV output needed by the
x-ray tube. The primary has 50 loops and draws a current of 10.00 A when in use. (a) What is the number of loops in the
secondary? (b) Find the current output of the secondary.
Strategy and Solution for (a)
We solve
Vs
Vp
=
Ns
Np
for Ns , the number of loops in the secondary, and enter the known values. This gives
(23.30)
Ns = Np
Vs
Vp
= (50)100,000 V
120 V
= 4.17×104
.
Discussion for (a)

A large number of loops in the secondary (compared with the primary) is required to produce such a large voltage. This
would be true for neon sign transformers and those supplying high voltage inside TVs and CRTs.
Strategy and Solution for (b)
We can similarly find the output current of the secondary by solving
Is
Ip
=
Np
Ns
for Is and entering known values. This gives
(23.31)
Is = Ip
Np
Ns
= (10.00 A) 50
4.17×104
= 12.0 mA.
Discussion for (b)
As expected, the current output is significantly less than the input. In certain spectacular demonstrations, very large voltages
are used to produce long arcs, but they are relatively safe because the transformer output does not supply a large current.
Note that the power input here is Pp = IpVp = (10.00 A)(120 V) = 1.20 kW . This equals the power output
Pp = IsVs = (12.0 mA)(100 kV) = 1.20 kW , as we assumed in the derivation of the equations used.
The fact that transformers are based on Faraday’s law of induction makes it clear why we cannot use transformers to change DC
voltages. If there is no change in primary voltage, there is no voltage induced in the secondary. One possibility is to connect DC
to the primary coil through a switch. As the switch is opened and closed, the secondary produces a voltage like that in Figure
23.29. This is not really a practical alternative, and AC is in common use wherever it is necessary to increase or decrease
voltages.
Figure 23.29 Transformers do not work for pure DC voltage input, but if it is switched on and off as on the top graph, the output will look something like
that on the bottom graph. This is not the sinusoidal AC most AC appliances need.
Example 23.6 Calculating Characteristics of a Step-Down Transformer
A battery charger meant for a series connection of ten nickel-cadmium batteries (total emf of 12.5 V DC) needs to have a
15.0 V output to charge the batteries. It uses a step-down transformer with a 200-loop primary and a 120 V input. (a) How
many loops should there be in the secondary coil? (b) If the charging current is 16.0 A, what is the input current?
You would expect the secondary to have a small number of loops. Solving
Vs
Vp
=
Ns
Np
for Ns and entering known values
gives

(23.32)
Ns = Np
Vs
Vp
= (200)15.0 V
120 V
= 25.
The current input can be obtained by solving
Is
Ip
=
Np
Ns
for Ip and entering known values. This gives
(23.33)
Ip = Is
Ns
Np
= (16.0 A) 25
200
= 2.00 A.
Discussion
The number of loops in the secondary is small, as expected for a step-down transformer. We also see that a small input
current produces a larger output current in a step-down transformer. When transformers are used to operate large magnets,
they sometimes have a small number of very heavy loops in the secondary. This allows the secondary to have low internal
resistance and produce large currents. Note again that this solution is based on the assumption of 100% efficiency—or
power out equals power in ( Pp = Ps )—reasonable for good transformers. In this case the primary and secondary power is
240 W. (Verify this for yourself as a consistency check.) Note that the Ni-Cd batteries need to be charged from a DC power
source (as would a 12 V battery). So the AC output of the secondary coil needs to be converted into DC. This is done using
something called a rectifier, which uses devices called diodes that allow only a one-way flow of current.
Transformers have many applications in electrical safety systems, which are discussed in Electrical Safety: Systems and
Devices.
PhET Explorations: Generator
Generate electricity with a bar magnet! Discover the physics behind the phenomena by exploring magnets and how you can
use them to make a bulb light.
Figure 23.30 Generator (http://cnx.org/content/m55414/1.2/generator_en.jar)
23.8 Electrical Safety: Systems and Devices
Learning Objectives
• Explain how various modern safety features in electric circuits work, with an emphasis on how induction is employed.
Electricity has two hazards. A thermal hazard occurs when there is electrical overheating. A shock hazard occurs when electric
current passes through a person. Both hazards have already been discussed. Here we will concentrate on systems and devices
that prevent electrical hazards.
Figure 23.31 shows the schematic for a simple AC circuit with no safety features. This is not how power is distributed in practice.
Modern household and industrial wiring requires the three-wire system, shown schematically in Figure 23.32, which has
several safety features. First is the familiar circuit breaker (or fuse) to prevent thermal overload. Second, there is a protective
case around the appliance, such as a toaster or refrigerator. The case’s safety feature is that it prevents a person from touching
exposed wires and coming into electrical contact with the circuit, helping prevent shocks.

Figure 23.31 Schematic of a simple AC circuit with a voltage source and a single appliance represented by the resistance R . There are no safety
features in this circuit.
Figure 23.32 The three-wire system connects the neutral wire to the earth at the voltage source and user location, forcing it to be at zero volts and
supplying an alternative return path for the current through the earth. Also grounded to zero volts is the case of the appliance. A circuit breaker or fuse
protects against thermal overload and is in series on the active (live/hot) wire. Note that wire insulation colors vary with region and it is essential to
check locally to determine which color codes are in use (and even if they were followed in the particular installation).
There are three connections to earth or ground (hereafter referred to as “earth/ground”) shown in Figure 23.32. Recall that an
earth/ground connection is a low-resistance path directly to the earth. The two earth/ground connections on the neutral wire force
it to be at zero volts relative to the earth, giving the wire its name. This wire is therefore safe to touch even if its insulation, usually
white, is missing. The neutral wire is the return path for the current to follow to complete the circuit. Furthermore, the two earth/
ground connections supply an alternative path through the earth, a good conductor, to complete the circuit. The earth/ground
connection closest to the power source could be at the generating plant, while the other is at the user’s location. The third earth/
ground is to the case of the appliance, through the green earth/ground wire, forcing the case, too, to be at zero volts. The live or
hot wire (hereafter referred to as “live/hot”) supplies voltage and current to operate the appliance. Figure 23.33 shows a more
pictorial version of how the three-wire system is connected through a three-prong plug to an appliance.
Figure 23.33 The standard three-prong plug can only be inserted in one way, to assure proper function of the three-wire system.

A note on insulation color-coding: Insulating plastic is color-coded to identify live/hot, neutral and ground wires but these codes
vary around the world. Live/hot wires may be brown, red, black, blue or grey. Neutral wire may be blue, black or white. Since the
same color may be used for live/hot or neutral in different parts of the world, it is essential to determine the color code in your
region. The only exception is the earth/ground wire which is often green but may be yellow or just bare wire. Striped coatings are
sometimes used for the benefit of those who are colorblind.
The three-wire system replaced the older two-wire system, which lacks an earth/ground wire. Under ordinary circumstances,
insulation on the live/hot and neutral wires prevents the case from being directly in the circuit, so that the earth/ground wire may
seem like double protection. Grounding the case solves more than one problem, however. The simplest problem is worn
insulation on the live/hot wire that allows it to contact the case, as shown in Figure 23.34. Lacking an earth/ground connection
(some people cut the third prong off the plug because they only have outdated two hole receptacles), a severe shock is possible.
This is particularly dangerous in the kitchen, where a good connection to earth/ground is available through water on the floor or a
water faucet. With the earth/ground connection intact, the circuit breaker will trip, forcing repair of the appliance. Why are some
appliances still sold with two-prong plugs? These have nonconducting cases, such as power tools with impact resistant plastic
cases, and are called doubly insulated. Modern two-prong plugs can be inserted into the asymmetric standard outlet in only one
way, to ensure proper connection of live/hot and neutral wires.
Figure 23.34 Worn insulation allows the live/hot wire to come into direct contact with the metal case of this appliance. (a) The earth/ground connection
being broken, the person is severely shocked. The appliance may operate normally in this situation. (b) With a proper earth/ground, the circuit breaker
trips, forcing repair of the appliance.
Electromagnetic induction causes a more subtle problem that is solved by grounding the case. The AC current in appliances can
induce an emf on the case. If grounded, the case voltage is kept near zero, but if the case is not grounded, a shock can occur as

pictured in Figure 23.35. Current driven by the induced case emf is called a leakage current, although current does not
necessarily pass from the resistor to the case.
Figure 23.35 AC currents can induce an emf on the case of an appliance. The voltage can be large enough to cause a shock. If the case is grounded,
the induced emf is kept near zero.
A ground fault interrupter (GFI) is a safety device found in updated kitchen and bathroom wiring that works based on
electromagnetic induction. GFIs compare the currents in the live/hot and neutral wires. When live/hot and neutral currents are not
equal, it is almost always because current in the neutral is less than in the live/hot wire. Then some of the current, again called a
leakage current, is returning to the voltage source by a path other than through the neutral wire. It is assumed that this path
presents a hazard, such as shown in Figure 23.36. GFIs are usually set to interrupt the circuit if the leakage current is greater
than 5 mA, the accepted maximum harmless shock. Even if the leakage current goes safely to earth/ground through an intact
earth/ground wire, the GFI will trip, forcing repair of the leakage.
Figure 23.36 A ground fault interrupter (GFI) compares the currents in the live/hot and neutral wires and will trip if their difference exceeds a safe
value. The leakage current here follows a hazardous path that could have been prevented by an intact earth/ground wire.
Figure 23.37 shows how a GFI works. If the currents in the live/hot and neutral wires are equal, then they induce equal and
opposite emfs in the coil. If not, then the circuit breaker will trip.

Figure 23.37 A GFI compares currents by using both to induce an emf in the same coil. If the currents are equal, they will induce equal but opposite
emfs.
Another induction-based safety device is the isolation transformer, shown in Figure 23.38. Most isolation transformers have
equal input and output voltages. Their function is to put a large resistance between the original voltage source and the device
being operated. This prevents a complete circuit between them, even in the circumstance shown. There is a complete circuit
through the appliance. But there is not a complete circuit for current to flow through the person in the figure, who is touching only
one of the transformer’s output wires, and neither output wire is grounded. The appliance is isolated from the original voltage
source by the high resistance of the material between the transformer coils, hence the name isolation transformer. For current to
flow through the person, it must pass through the high-resistance material between the coils, through the wire, the person, and
back through the earth—a path with such a large resistance that the current is negligible.
Figure 23.38 An isolation transformer puts a large resistance between the original voltage source and the device, preventing a complete circuit
between them.
The basics of electrical safety presented here help prevent many electrical hazards. Electrical safety can be pursued to greater
depths. There are, for example, problems related to different earth/ground connections for appliances in close proximity. Many
other examples are found in hospitals. Microshock-sensitive patients, for instance, require special protection. For these people,
currents as low as 0.1 mA may cause ventricular fibrillation. The interested reader can use the material presented here as a
basis for further study.
23.9 Inductance
Learning Objectives
• Calculate the inductance of an inductor.
• Calculate the energy stored in an inductor.
• Calculate the emf generated in an inductor.
Inductors
Induction is the process in which an emf is induced by changing magnetic flux. Many examples have been discussed so far,
some more effective than others. Transformers, for example, are designed to be particularly effective at inducing a desired
voltage and current with very little loss of energy to other forms. Is there a useful physical quantity related to how “effective” a
given device is? The answer is yes, and that physical quantity is called inductance.
Mutual inductance is the effect of Faraday’s law of induction for one device upon another, such as the primary coil in
transmitting energy to the secondary in a transformer. See Figure 23.39, where simple coils induce emfs in one another.

Figure 23.39 These coils can induce emfs in one another like an inefficient transformer. Their mutual inductance M indicates the effectiveness of the
coupling between them. Here a change in current in coil 1 is seen to induce an emf in coil 2. (Note that " E2 induced" represents the induced emf in
coil 2.)
In the many cases where the geometry of the devices is fixed, flux is changed by varying current. We therefore concentrate on
the rate of change of current, ΔI/Δt , as the cause of induction. A change in the current I1 in one device, coil 1 in the figure,
induces an emf2 in the other. We express this in equation form as
(23.34)
emf2 = −M
ΔI1
Δt
,
where M is defined to be the mutual inductance between the two devices. The minus sign is an expression of Lenz’s law. The
larger the mutual inductance M , the more effective the coupling. For example, the coils in Figure 23.39 have a small M
compared with the transformer coils in Figure 23.28. Units for M are (V ⋅ s)/A = Ω ⋅ s , which is named a henry (H), after
Joseph Henry. That is, 1 H = 1 Ω ⋅ s .
Nature is symmetric here. If we change the current I2 in coil 2, we induce an emf1 in coil 1, which is given by
(23.35)
emf1 = −M
ΔI2
Δt
,
where M is the same as for the reverse process. Transformers run backward with the same effectiveness, or mutual inductance
M .
A large mutual inductance M may or may not be desirable. We want a transformer to have a large mutual inductance. But an
appliance, such as an electric clothes dryer, can induce a dangerous emf on its case if the mutual inductance between its coils
and the case is large. One way to reduce mutual inductance M is to counterwind coils to cancel the magnetic field produced.
(See Figure 23.40.)

Figure 23.40 The heating coils of an electric clothes dryer can be counter-wound so that their magnetic fields cancel one another, greatly reducing the
mutual inductance with the case of the dryer.
Self-inductance, the effect of Faraday’s law of induction of a device on itself, also exists. When, for example, current through a
coil is increased, the magnetic field and flux also increase, inducing a counter emf, as required by Lenz’s law. Conversely, if the
current is decreased, an emf is induced that opposes the decrease. Most devices have a fixed geometry, and so the change in
flux is due entirely to the change in current ΔI through the device. The induced emf is related to the physical geometry of the
device and the rate of change of current. It is given by
(23.36)
emf = −LΔI
Δt
,
where L is the self-inductance of the device. A device that exhibits significant self-inductance is called an inductor, and given
the symbol in Figure 23.41.
Figure 23.41
The minus sign is an expression of Lenz’s law, indicating that emf opposes the change in current. Units of self-inductance are
henries (H) just as for mutual inductance. The larger the self-inductance L of a device, the greater its opposition to any change
in current through it. For example, a large coil with many turns and an iron core has a large L and will not allow current to
change quickly. To avoid this effect, a small L must be achieved, such as by counterwinding coils as in Figure 23.40.
A 1 H inductor is a large inductor. To illustrate this, consider a device with L = 1.0 H that has a 10 A current flowing through it.
What happens if we try to shut off the current rapidly, perhaps in only 1.0 ms? An emf, given by emf = −L(ΔI / Δt) , will
oppose the change. Thus an emf will be induced given by emf = −L(ΔI / Δt) = (1.0 H)[(10 A) / (1.0 ms)] = 10,000 V .
The positive sign means this large voltage is in the same direction as the current, opposing its decrease. Such large emfs can
cause arcs, damaging switching equipment, and so it may be necessary to change current more slowly.
There are uses for such a large induced voltage. Camera flashes use a battery, two inductors that function as a transformer, and
a switching system or oscillator to induce large voltages. (Remember that we need a changing magnetic field, brought about by a
changing current, to induce a voltage in another coil.) The oscillator system will do this many times as the battery voltage is
boosted to over one thousand volts. (You may hear the high pitched whine from the transformer as the capacitor is being
charged.) A capacitor stores the high voltage for later use in powering the flash. (See Figure 23.42.)

Figure 23.42 Through rapid switching of an inductor, 1.5 V batteries can be used to induce emfs of several thousand volts. This voltage can be used to
store charge in a capacitor for later use, such as in a camera flash attachment.
It is possible to calculate L for an inductor given its geometry (size and shape) and knowing the magnetic field that it produces.
This is difficult in most cases, because of the complexity of the field created. So in this text the inductance L is usually a given
quantity. One exception is the solenoid, because it has a very uniform field inside, a nearly zero field outside, and a simple
shape. It is instructive to derive an equation for its inductance. We start by noting that the induced emf is given by Faraday’s law
of induction as emf = −N(ΔΦ / Δt) and, by the definition of self-inductance, as emf = −L(ΔI / Δt) . Equating these yields
(23.37)
emf = −NΔΦ
Δt
= −LΔI
Δt
.
Solving for L gives
(23.38)
L = NΔΦ
ΔI
.
This equation for the self-inductance L of a device is always valid. It means that self-inductance L depends on how effective
the current is in creating flux; the more effective, the greater ΔΦ / ΔI is.
Let us use this last equation to find an expression for the inductance of a solenoid. Since the area A of a solenoid is fixed, the
change in flux is ΔΦ = Δ(BA) = AΔB . To find ΔB , we note that the magnetic field of a solenoid is given by
B = µ0nI = µ0
NI
ℓ
. (Here n = N / ℓ , where N is the number of coils and ℓ is the solenoid’s length.) Only the current
changes, so that ΔΦ = AΔB = µ0NAΔI
ℓ
. Substituting ΔΦ into L = NΔΦ
ΔI
gives
(23.39)
L = NΔΦ
ΔI
= N
µ0 NAΔI
ℓ
ΔI
.
This simplifies to
(23.40)
L =
µ0 N2
A
ℓ
(solenoid).
This is the self-inductance of a solenoid of cross-sectional area A and length ℓ . Note that the inductance depends only on the
physical characteristics of the solenoid, consistent with its definition.
Example 23.7 Calculating the Self-inductance of a Moderate Size Solenoid
Calculate the self-inductance of a 10.0 cm long, 4.00 cm diameter solenoid that has 200 coils.
Strategy
This is a straightforward application of L =
µ0 N2
A
ℓ
, since all quantities in the equation except L are known.
Solution
Use the following expression for the self-inductance of a solenoid:
(23.41)
L =
µ0 N2
A
ℓ
.

The cross-sectional area in this example is A = πr2
= (3.14...)(0.0200 m)2
= 1.26×10−3
m2
, N is given to be 200,
and the length ℓ is 0.100 m. We know the permeability of free space is µ0 = 4π×10−7
T ⋅ m/A . Substituting these into
the expression for L gives
(23.42)
L =
(4π×10−7
T ⋅ m/A)(200)2
(1.26×10−3
m2
)
0.100 m
= 0.632 mH.
Discussion
This solenoid is moderate in size. Its inductance of nearly a millihenry is also considered moderate.
One common application of inductance is used in traffic lights that can tell when vehicles are waiting at the intersection. An
electrical circuit with an inductor is placed in the road under the place a waiting car will stop over. The body of the car increases
the inductance and the circuit changes sending a signal to the traffic lights to change colors. Similarly, metal detectors used for
airport security employ the same technique. A coil or inductor in the metal detector frame acts as both a transmitter and a
receiver. The pulsed signal in the transmitter coil induces a signal in the receiver. The self-inductance of the circuit is affected by
any metal object in the path. Such detectors can be adjusted for sensitivity and also can indicate the approximate location of
metal found on a person. (But they will not be able to detect any plastic explosive such as that found on the “underwear
bomber.”) See Figure 23.43.
Figure 23.43 The familiar security gate at an airport can not only detect metals but also indicate their approximate height above the floor. (credit:
Alexbuirds, Wikimedia Commons)
Energy Stored in an Inductor
We know from Lenz’s law that inductances oppose changes in current. There is an alternative way to look at this opposition that
is based on energy. Energy is stored in a magnetic field. It takes time to build up energy, and it also takes time to deplete energy;
hence, there is an opposition to rapid change. In an inductor, the magnetic field is directly proportional to current and to the
inductance of the device. It can be shown that the energy stored in an inductor Eind is given by
(23.43)
Eind = 1
2
LI2
.
This expression is similar to that for the energy stored in a capacitor.
Example 23.8 Calculating the Energy Stored in the Field of a Solenoid
How much energy is stored in the 0.632 mH inductor of the preceding example when a 30.0 A current flows through it?
Strategy
The energy is given by the equation Eind = 1
2
LI2
, and all quantities except Eind are known.
Solution
Substituting the value for L found in the previous example and the given current into Eind = 1
2
LI2
gives
(23.44)
Eind = 1
2
LI2
= 0.5(0.632×10−3
H)(30.0 A)2
= 0.284 J.

Discussion
This amount of energy is certainly enough to cause a spark if the current is suddenly switched off. It cannot be built up
instantaneously unless the power input is infinite.
23.10 RL Circuits
Learning Objectives
• Calculate the current in an RL circuit after a specified number of characteristic time steps.
• Calculate the characteristic time of an RL circuit.
• Sketch the current in an RL circuit over time.
We know that the current through an inductor L cannot be turned on or off instantaneously. The change in current changes flux,
inducing an emf opposing the change (Lenz’s law). How long does the opposition last? Current will flow and can be turned off,
but how long does it take? Figure 23.44 shows a switching circuit that can be used to examine current through an inductor as a
function of time.
Figure 23.44 (a) An RL circuit with a switch to turn current on and off. When in position 1, the battery, resistor, and inductor are in series and a current
is established. In position 2, the battery is removed and the current eventually stops because of energy loss in the resistor. (b) A graph of current
growth versus time when the switch is moved to position 1. (c) A graph of current decay when the switch is moved to position 2.
When the switch is first moved to position 1 (at t = 0 ), the current is zero and it eventually rises to I0 = V/R , where R is the
total resistance of the circuit. The opposition of the inductor L is greatest at the beginning, because the amount of change is
greatest. The opposition it poses is in the form of an induced emf, which decreases to zero as the current approaches its final
value. The opposing emf is proportional to the amount of change left. This is the hallmark of an exponential behavior, and it can
be shown with calculus that
(23.45)I = I0(1 − e−t / τ
) (turning on),
is the current in an RL circuit when switched on (Note the similarity to the exponential behavior of the voltage on a charging
capacitor). The initial current is zero and approaches I0 = V/R with a characteristic time constant τ for an RL circuit, given
by
(23.46)
τ = L
R
,
where τ has units of seconds, since 1 H=1 Ω·s . In the first period of time τ , the current rises from zero to 0.632I0 , since
I = I0(1 − e−1
) = I0(1 − 0.368) = 0.632I0 . The current will go 0.632 of the remainder in the next time τ . A well-known
property of the exponential is that the final value is never exactly reached, but 0.632 of the remainder to that value is achieved in
every characteristic time τ . In just a few multiples of the time τ , the final value is very nearly achieved, as the graph in Figure
23.44(b) illustrates.
The characteristic time τ depends on only two factors, the inductance L and the resistance R . The greater the inductance L ,
the greater τ is, which makes sense since a large inductance is very effective in opposing change. The smaller the resistance
R , the greater τ is. Again this makes sense, since a small resistance means a large final current and a greater change to get
there. In both cases—large L and small R —more energy is stored in the inductor and more time is required to get it in and
out.

When the switch in Figure 23.44(a) is moved to position 2 and cuts the battery out of the circuit, the current drops because of
energy dissipation by the resistor. But this is also not instantaneous, since the inductor opposes the decrease in current by
inducing an emf in the same direction as the battery that drove the current. Furthermore, there is a certain amount of energy,
(1/2)LI0
2
, stored in the inductor, and it is dissipated at a finite rate. As the current approaches zero, the rate of decrease slows,
since the energy dissipation rate is I2
R . Once again the behavior is exponential, and I is found to be
(23.47)I = I0e−t / τ
(turning off).
(See Figure 23.44(c).) In the first period of time τ = L / R after the switch is closed, the current falls to 0.368 of its initial value,
since I = I0e−1
= 0.368I0 . In each successive time τ , the current falls to 0.368 of the preceding value, and in a few
multiples of τ , the current becomes very close to zero, as seen in the graph in Figure 23.44(c).
Example 23.9 Calculating Characteristic Time and Current in an RL Circuit
(a) What is the characteristic time constant for a 7.50 mH inductor in series with a 3.00 Ω resistor? (b) Find the current
5.00 ms after the switch is moved to position 2 to disconnect the battery, if it is initially 10.0 A.
Strategy for (a)
The time constant for an RL circuit is defined by τ = L / R .
Solution for (a)
Entering known values into the expression for τ given in τ = L / R yields
(23.48)
τ = L
R
= 7.50 mH
3.00 Ω
= 2.50 ms.
Discussion for (a)
This is a small but definitely finite time. The coil will be very close to its full current in about ten time constants, or about 25
ms.
Strategy for (b)
We can find the current by using I = I0e−t / τ
, or by considering the decline in steps. Since the time is twice the
characteristic time, we consider the process in steps.
Solution for (b)
In the first 2.50 ms, the current declines to 0.368 of its initial value, which is
(23.49)I = 0.368I0 = (0.368)(10.0 A)
= 3.68 A at t = 2.50 ms.
After another 2.50 ms, or a total of 5.00 ms, the current declines to 0.368 of the value just found. That is,
(23.50)I′ = 0.368I = (0.368)(3.68 A)
= 1.35 A at t = 5.00 ms.
Discussion for (b)
After another 5.00 ms has passed, the current will be 0.183 A (see Exercise 23.69); so, although it does die out, the current
certainly does not go to zero instantaneously.
In summary, when the voltage applied to an inductor is changed, the current also changes, but the change in current lags the
change in voltage in an RL circuit. In Reactance, Inductive and Capacitive, we explore how an RL circuit behaves when a
sinusoidal AC voltage is applied.
23.11 Reactance, Inductive and Capacitive
Learning Objectives
• Sketch voltage and current versus time in simple inductive, capacitive, and resistive circuits.
• Calculate inductive and capacitive reactance.
• Calculate current and/or voltage in simple inductive, capacitive, and resistive circuits.

Many circuits also contain capacitors and inductors, in addition to resistors and an AC voltage source. We have seen how
capacitors and inductors respond to DC voltage when it is switched on and off. We will now explore how inductors and capacitors
react to sinusoidal AC voltage.
Inductors and Inductive Reactance
Suppose an inductor is connected directly to an AC voltage source, as shown in Figure 23.45. It is reasonable to assume
negligible resistance, since in practice we can make the resistance of an inductor so small that it has a negligible effect on the
circuit. Also shown is a graph of voltage and current as functions of time.
Figure 23.45 (a) An AC voltage source in series with an inductor having negligible resistance. (b) Graph of current and voltage across the inductor as
functions of time.
The graph in Figure 23.45(b) starts with voltage at a maximum. Note that the current starts at zero and rises to its peak after the
voltage that drives it, just as was the case when DC voltage was switched on in the preceding section. When the voltage
becomes negative at point a, the current begins to decrease; it becomes zero at point b, where voltage is its most negative. The
current then becomes negative, again following the voltage. The voltage becomes positive at point c and begins to make the
current less negative. At point d, the current goes through zero just as the voltage reaches its positive peak to start another
cycle. This behavior is summarized as follows:
AC Voltage in an Inductor
When a sinusoidal voltage is applied to an inductor, the voltage leads the current by one-fourth of a cycle, or by a 90º
phase angle.
Current lags behind voltage, since inductors oppose change in current. Changing current induces a back emf V = −L(ΔI / Δt)
. This is considered to be an effective resistance of the inductor to AC. The rms current I through an inductor L is given by a
version of Ohm’s law:
(23.51)
I = V
XL
,
where V is the rms voltage across the inductor and XL is defined to be
(23.52)XL = 2πfL,
with f the frequency of the AC voltage source in hertz (An analysis of the circuit using Kirchhoff’s loop rule and calculus actually
produces this expression). XL is called the inductive reactance, because the inductor reacts to impede the current. XL has
units of ohms ( 1 H = 1 Ω ⋅ s , so that frequency times inductance has units of (cycles/s)( Ω ⋅ s) = Ω ), consistent with its
role as an effective resistance. It makes sense that XL is proportional to L , since the greater the induction the greater its
resistance to change. It is also reasonable that XL is proportional to frequency f , since greater frequency means greater
change in current. That is, ΔI/Δt is large for large frequencies (large f , small Δt ). The greater the change, the greater the
opposition of an inductor.
Example 23.10 Calculating Inductive Reactance and then Current
(a) Calculate the inductive reactance of a 3.00 mH inductor when 60.0 Hz and 10.0 kHz AC voltages are applied. (b) What is
the rms current at each frequency if the applied rms voltage is 120 V?
Strategy

The inductive reactance is found directly from the expression XL = 2πfL . Once XL has been found at each frequency,
Ohm’s law as stated in the Equation I = V / XL can be used to find the current at each frequency.
Solution for (a)
Entering the frequency and inductance into Equation XL = 2πfL gives
(23.53)XL = 2πfL = 6.28(60.0 / s)(3.00 mH) = 1.13 Ω at 60 Hz.
Similarly, at 10 kHz,
(23.54)XL = 2πfL = 6.28(1.00×104
/s)(3.00 mH) = 188 Ω at 10 kHz.
Solution for (b)
The rms current is now found using the version of Ohm’s law in Equation I = V / XL , given the applied rms voltage is 120
V. For the first frequency, this yields
(23.55)
I = V
XL
= 120 V
1.13 Ω
= 106 A at 60 Hz.
(23.56)
I = V
XL
= 120 V
188 Ω
= 0.637 A at 10 kHz.
Discussion
The inductor reacts very differently at the two different frequencies. At the higher frequency, its reactance is large and the
current is small, consistent with how an inductor impedes rapid change. Thus high frequencies are impeded the most.
Inductors can be used to filter out high frequencies; for example, a large inductor can be put in series with a sound
reproduction system or in series with your home computer to reduce high-frequency sound output from your speakers or
high-frequency power spikes into your computer.
Note that although the resistance in the circuit considered is negligible, the AC current is not extremely large because inductive
reactance impedes its flow. With AC, there is no time for the current to become extremely large.
Capacitors and Capacitive Reactance
Consider the capacitor connected directly to an AC voltage source as shown in Figure 23.46. The resistance of a circuit like this
can be made so small that it has a negligible effect compared with the capacitor, and so we can assume negligible resistance.
Voltage across the capacitor and current are graphed as functions of time in the figure.
Figure 23.46 (a) An AC voltage source in series with a capacitor C having negligible resistance. (b) Graph of current and voltage across the capacitor
as functions of time.
The graph in Figure 23.46 starts with voltage across the capacitor at a maximum. The current is zero at this point, because the
capacitor is fully charged and halts the flow. Then voltage drops and the current becomes negative as the capacitor discharges.
At point a, the capacitor has fully discharged ( Q = 0 on it) and the voltage across it is zero. The current remains negative
between points a and b, causing the voltage on the capacitor to reverse. This is complete at point b, where the current is zero
and the voltage has its most negative value. The current becomes positive after point b, neutralizing the charge on the capacitor
and bringing the voltage to zero at point c, which allows the current to reach its maximum. Between points c and d, the current
drops to zero as the voltage rises to its peak, and the process starts to repeat. Throughout the cycle, the voltage follows what the
current is doing by one-fourth of a cycle:

AC Voltage in a Capacitor
When a sinusoidal voltage is applied to a capacitor, the voltage follows the current by one-fourth of a cycle, or by a 90º
phase angle.
The capacitor is affecting the current, having the ability to stop it altogether when fully charged. Since an AC voltage is applied,
there is an rms current, but it is limited by the capacitor. This is considered to be an effective resistance of the capacitor to AC,
and so the rms current I in the circuit containing only a capacitor C is given by another version of Ohm’s law to be
(23.57)
I = V
XC
,
where V is the rms voltage and XC is defined (As with XL , this expression for XC results from an analysis of the circuit
using Kirchhoff’s rules and calculus) to be
(23.58)
XC = 1
2πfC
,
where XC is called the capacitive reactance, because the capacitor reacts to impede the current. XC has units of ohms
(verification left as an exercise for the reader). XC is inversely proportional to the capacitance C ; the larger the capacitor, the
greater the charge it can store and the greater the current that can flow. It is also inversely proportional to the frequency f ; the
greater the frequency, the less time there is to fully charge the capacitor, and so it impedes current less.
Example 23.11 Calculating Capacitive Reactance and then Current
(a) Calculate the capacitive reactance of a 5.00 mF capacitor when 60.0 Hz and 10.0 kHz AC voltages are applied. (b) What
is the rms current if the applied rms voltage is 120 V?
Strategy
The capacitive reactance is found directly from the expression in XC = 1
2πfC
. Once XC has been found at each
frequency, Ohm’s law stated as I = V / XC can be used to find the current at each frequency.
Solution for (a)
Entering the frequency and capacitance into XC = 1
2πfC
gives
(23.59)
XC = 1
2πfC
= 1
6.28(60.0 / s)(5.00 µF)
= 531 Ω at 60 Hz.
(23.60)
XC = 1
2πfC
= 1
6.28(1.00×104
/ s)(5.00 µF)
= 3.18 Ω at 10 kHz
.
Solution for (b)
The rms current is now found using the version of Ohm’s law in I = V / XC , given the applied rms voltage is 120 V. For the
first frequency, this yields
(23.61)
I = V
XC
= 120 V
531 Ω
= 0.226 A at 60 Hz.
(23.62)
I = V
XC
= 120 V
3.18 Ω
= 37.7 A at 10 kHz.
Discussion
The capacitor reacts very differently at the two different frequencies, and in exactly the opposite way an inductor reacts. At
the higher frequency, its reactance is small and the current is large. Capacitors favor change, whereas inductors oppose
change. Capacitors impede low frequencies the most, since low frequency allows them time to become charged and stop

the current. Capacitors can be used to filter out low frequencies. For example, a capacitor in series with a sound
reproduction system rids it of the 60 Hz hum.
Although a capacitor is basically an open circuit, there is an rms current in a circuit with an AC voltage applied to a capacitor.
This is because the voltage is continually reversing, charging and discharging the capacitor. If the frequency goes to zero (DC),
XC tends to infinity, and the current is zero once the capacitor is charged. At very high frequencies, the capacitor’s reactance
tends to zero—it has a negligible reactance and does not impede the current (it acts like a simple wire). Capacitors have the
opposite effect on AC circuits that inductors have.
Resistors in an AC Circuit
Just as a reminder, consider Figure 23.47, which shows an AC voltage applied to a resistor and a graph of voltage and current
versus time. The voltage and current are exactly in phase in a resistor. There is no frequency dependence to the behavior of
plain resistance in a circuit:
Figure 23.47 (a) An AC voltage source in series with a resistor. (b) Graph of current and voltage across the resistor as functions of time, showing them
to be exactly in phase.
AC Voltage in a Resistor
When a sinusoidal voltage is applied to a resistor, the voltage is exactly in phase with the current—they have a 0º phase
angle.
23.12 RLC Series AC Circuits
Learning Objectives
• Calculate the impedance, phase angle, resonant frequency, power, power factor, voltage, and/or current in an RLC
series circuit.
• Draw the circuit diagram for an RLC series circuit.
• Explain the significance of the resonant frequency.
Impedance
When alone in an AC circuit, inductors, capacitors, and resistors all impede current. How do they behave when all three occur
together? Interestingly, their individual resistances in ohms do not simply add. Because inductors and capacitors behave in
opposite ways, they partially to totally cancel each other’s effect. Figure 23.48 shows an RLC series circuit with an AC voltage
source, the behavior of which is the subject of this section. The crux of the analysis of an RLC circuit is the frequency
dependence of XL and XC , and the effect they have on the phase of voltage versus current (established in the preceding
section). These give rise to the frequency dependence of the circuit, with important “resonance” features that are the basis of
many applications, such as radio tuners.

Figure 23.48 An RLC series circuit with an AC voltage source.
The combined effect of resistance R , inductive reactance XL , and capacitive reactance XC is defined to be impedance, an
AC analogue to resistance in a DC circuit. Current, voltage, and impedance in an RLC circuit are related by an AC version of
Ohm’s law:
(23.63)
I0 =
V0
Z
or Irms =
Vrms
Z
.
Here I0 is the peak current, V0 the peak source voltage, and Z is the impedance of the circuit. The units of impedance are
ohms, and its effect on the circuit is as you might expect: the greater the impedance, the smaller the current. To get an
expression for Z in terms of R , XL , and XC , we will now examine how the voltages across the various components are
related to the source voltage. Those voltages are labeled VR , VL , and VC in Figure 23.48.
Conservation of charge requires current to be the same in each part of the circuit at all times, so that we can say the currents in
R , L , and C are equal and in phase. But we know from the preceding section that the voltage across the inductor VL leads
the current by one-fourth of a cycle, the voltage across the capacitor VC follows the current by one-fourth of a cycle, and the
voltage across the resistor VR is exactly in phase with the current. Figure 23.49 shows these relationships in one graph, as well
as showing the total voltage around the circuit V = VR + VL + VC , where all four voltages are the instantaneous values.
According to Kirchhoff’s loop rule, the total voltage around the circuit V is also the voltage of the source.
You can see from Figure 23.49 that while VR is in phase with the current, VL leads by 90º , and VC follows by 90º . Thus
VL and VC are 180º out of phase (crest to trough) and tend to cancel, although not completely unless they have the same
magnitude. Since the peak voltages are not aligned (not in phase), the peak voltage V0 of the source does not equal the sum of
the peak voltages across R , L , and C . The actual relationship is
(23.64)
V0 = V0R
2
+(V0L − V0C)2
,
where V0R , V0L , and V0C are the peak voltages across R , L , and C , respectively. Now, using Ohm’s law and definitions
from Reactance, Inductive and Capacitive, we substitute V0 = I0Z into the above, as well as V0R = I0R , V0L = I0XL ,
and V0C = I0XC , yielding
(23.65)
I0 Z = I0
2
R2
+ (I0 XL − I0XC )2
= I0 R2
+ (XL − XC)2
.
I0 cancels to yield an expression for Z :
(23.66)
Z = R2
+ (XL − XC)2
,
which is the impedance of an RLC series AC circuit. For circuits without a resistor, take R = 0 ; for those without an inductor,
take XL = 0 ; and for those without a capacitor, take XC = 0 .

Figure 23.49 This graph shows the relationships of the voltages in an RLC circuit to the current. The voltages across the circuit elements add to equal
the voltage of the source, which is seen to be out of phase with the current.
Example 23.12 Calculating Impedance and Current
An RLC series circuit has a 40.0 Ω resistor, a 3.00 mH inductor, and a 5.00 μF capacitor. (a) Find the circuit’s impedance
at 60.0 Hz and 10.0 kHz, noting that these frequencies and the values for L and C are the same as in Example 23.10 and
Example 23.11. (b) If the voltage source has Vrms = 120 V , what is Irms at each frequency?
Strategy
For each frequency, we use Z = R2
+ (XL − XC)2
to find the impedance and then Ohm’s law to find current. We can
take advantage of the results of the previous two examples rather than calculate the reactances again.
Solution for (a)
At 60.0 Hz, the values of the reactances were found in Example 23.10 to be XL = 1.13 Ω and in Example 23.11 to be
XC = 531 Ω . Entering these and the given 40.0 Ω for resistance into Z = R2
+ (XL − XC)2
yields
(23.67)
Z = R2
+ (XL − XC)2
= (40.0 Ω )2
+ (1.13 Ω − 531 Ω )2
= 531 Ω at 60.0 Hz.
Similarly, at 10.0 kHz, XL = 188 Ω and XC = 3.18 Ω , so that
(23.68)
Z = (40.0 Ω )2
+ (188 Ω − 3.18 Ω )2
= 190 Ω at 10.0 kHz.
Discussion for (a)
In both cases, the result is nearly the same as the largest value, and the impedance is definitely not the sum of the individual
values. It is clear that XL dominates at high frequency and XC dominates at low frequency.
Solution for (b)
The current Irms can be found using the AC version of Ohm’s law in Equation Irms = Vrms / Z :
Irms =
Vrms
Z
= 120 V
531 Ω
= 0.226 A at 60.0 Hz
Finally, at 10.0 kHz, we find
Irms =
Vrms
Z
= 120 V
190 Ω
= 0.633 A at 10.0 kHz
Discussion for (a)

The current at 60.0 Hz is the same (to three digits) as found for the capacitor alone in Example 23.11. The capacitor
dominates at low frequency. The current at 10.0 kHz is only slightly different from that found for the inductor alone in
Example 23.10. The inductor dominates at high frequency.
Resonance in RLC Series AC Circuits
How does an RLC circuit behave as a function of the frequency of the driving voltage source? Combining Ohm’s law,
Irms = Vrms / Z , and the expression for impedance Z from Z = R2
+ (XL − XC)2
gives
(23.69)
Irms =
Vrms
R2
+ (XL − XC)2
.
The reactances vary with frequency, with XL large at high frequencies and XC large at low frequencies, as we have seen in
three previous examples. At some intermediate frequency f0 , the reactances will be equal and cancel, giving Z = R —this is a
minimum value for impedance, and a maximum value for Irms results. We can get an expression for f0 by taking
(23.70)XL = XC.
Substituting the definitions of XL and XC ,
(23.71)
2πf0 L = 1
2πf0 C
.
Solving this expression for f0 yields
(23.72)
f0 = 1
2π LC
,
where f0 is the resonant frequency of an RLC series circuit. This is also the natural frequency at which the circuit would
oscillate if not driven by the voltage source. At f0 , the effects of the inductor and capacitor cancel, so that Z = R , and Irms is
a maximum.
Resonance in AC circuits is analogous to mechanical resonance, where resonance is defined to be a forced oscillation—in this
case, forced by the voltage source—at the natural frequency of the system. The receiver in a radio is an RLC circuit that
oscillates best at its f0 . A variable capacitor is often used to adjust f0 to receive a desired frequency and to reject others.
Figure 23.50 is a graph of current as a function of frequency, illustrating a resonant peak in Irms at f0 . The two curves are for
two different circuits, which differ only in the amount of resistance in them. The peak is lower and broader for the higher-
resistance circuit. Thus the higher-resistance circuit does not resonate as strongly and would not be as selective in a radio
receiver, for example.
Figure 23.50 A graph of current versus frequency for two RLC series circuits differing only in the amount of resistance. Both have a resonance at f0 ,
but that for the higher resistance is lower and broader. The driving AC voltage source has a fixed amplitude V0 .
Example 23.13 Calculating Resonant Frequency and Current
For the same RLC series circuit having a 40.0 Ω resistor, a 3.00 mH inductor, and a 5.00 μF capacitor: (a) Find the
resonant frequency. (b) Calculate Irms at resonance if Vrms is 120 V.
Strategy

The resonant frequency is found by using the expression in f0 = 1
2π LC
. The current at that frequency is the same as if
the resistor alone were in the circuit.
Solution for (a)
Entering the given values for L and C into the expression given for f0 in f0 = 1
2π LC
yields
(23.73)
f0 = 1
2π LC
= 1
2π (3.00×10−3
H)(5.00×10−6
F)
= 1.30 kHz.
Discussion for (a)
We see that the resonant frequency is between 60.0 Hz and 10.0 kHz, the two frequencies chosen in earlier examples. This
was to be expected, since the capacitor dominated at the low frequency and the inductor dominated at the high frequency.
Their effects are the same at this intermediate frequency.
Solution for (b)
The current is given by Ohm’s law. At resonance, the two reactances are equal and cancel, so that the impedance equals
the resistance alone. Thus,
(23.74)
Irms =
Vrms
Z
= 120 V
40.0 Ω
= 3.00 A.
Discussion for (b)
At resonance, the current is greater than at the higher and lower frequencies considered for the same circuit in the
preceding example.
Power in RLC Series AC Circuits
If current varies with frequency in an RLC circuit, then the power delivered to it also varies with frequency. But the average power
is not simply current times voltage, as it is in purely resistive circuits. As was seen in Figure 23.49, voltage and current are out of
phase in an RLC circuit. There is a phase angle ϕ between the source voltage V and the current I , which can be found from
(23.75)
cos ϕ = R
Z
.
For example, at the resonant frequency or in a purely resistive circuit Z = R , so that cos ϕ = 1 . This implies that ϕ = 0 º
and that voltage and current are in phase, as expected for resistors. At other frequencies, average power is less than at
resonance. This is both because voltage and current are out of phase and because Irms is lower. The fact that source voltage
and current are out of phase affects the power delivered to the circuit. It can be shown that the average power is
(23.76)Pave = IrmsVrms cos ϕ,
Thus cos ϕ is called the power factor, which can range from 0 to 1. Power factors near 1 are desirable when designing an
efficient motor, for example. At the resonant frequency, cos ϕ = 1 .
Example 23.14 Calculating the Power Factor and Power
For the same RLC series circuit having a 40.0 Ω resistor, a 3.00 mH inductor, a 5.00 μF capacitor, and a voltage source
with a Vrms of 120 V: (a) Calculate the power factor and phase angle for f = 60.0Hz . (b) What is the average power at
50.0 Hz? (c) Find the average power at the circuit’s resonant frequency.
The power factor at 60.0 Hz is found from
(23.77)
cos ϕ = R
Z
.
We know Z= 531 Ω from Example 23.12, so that
(23.78)
cos ϕ = 40.0 Ω
531 Ω
= 0.0753 at 60.0 Hz.

This small value indicates the voltage and current are significantly out of phase. In fact, the phase angle is
(23.79)ϕ = cos−1
0.0753 = 85.7º at 60.0 Hz.
Discussion for (a)
The phase angle is close to 90º , consistent with the fact that the capacitor dominates the circuit at this low frequency (a
pure RC circuit has its voltage and current 90º out of phase).
The average power at 60.0 Hz is
(23.80)Pave = IrmsVrms cos ϕ.
Irms was found to be 0.226 A in Example 23.12. Entering the known values gives
(23.81)Pave = (0.226 A)(120 V)(0.0753) = 2.04 W at 60.0 Hz.
Strategy and Solution for (c)
At the resonant frequency, we know cos ϕ = 1 , and Irms was found to be 6.00 A in Example 23.13. Thus,
Pave = (3.00 A)(120 V)(1) = 360 W at resonance (1.30 kHz)
Discussion
Both the current and the power factor are greater at resonance, producing significantly greater power than at higher and
lower frequencies.
Power delivered to an RLC series AC circuit is dissipated by the resistance alone. The inductor and capacitor have energy input
and output but do not dissipate it out of the circuit. Rather they transfer energy back and forth to one another, with the resistor
dissipating exactly what the voltage source puts into the circuit. This assumes no significant electromagnetic radiation from the
inductor and capacitor, such as radio waves. Such radiation can happen and may even be desired, as we will see in the next
chapter on electromagnetic radiation, but it can also be suppressed as is the case in this chapter. The circuit is analogous to the
wheel of a car driven over a corrugated road as shown in Figure 23.51. The regularly spaced bumps in the road are analogous
to the voltage source, driving the wheel up and down. The shock absorber is analogous to the resistance damping and limiting
the amplitude of the oscillation. Energy within the system goes back and forth between kinetic (analogous to maximum current,
and energy stored in an inductor) and potential energy stored in the car spring (analogous to no current, and energy stored in the
electric field of a capacitor). The amplitude of the wheels’ motion is a maximum if the bumps in the road are hit at the resonant
frequency.
Figure 23.51 The forced but damped motion of the wheel on the car spring is analogous to an RLC series AC circuit. The shock absorber damps the
motion and dissipates energy, analogous to the resistance in an RLC circuit. The mass and spring determine the resonant frequency.
A pure LC circuit with negligible resistance oscillates at f0 , the same resonant frequency as an RLC circuit. It can serve as a
frequency standard or clock circuit—for example, in a digital wristwatch. With a very small resistance, only a very small energy
input is necessary to maintain the oscillations. The circuit is analogous to a car with no shock absorbers. Once it starts
oscillating, it continues at its natural frequency for some time. Figure 23.52 shows the analogy between an LC circuit and a mass
on a spring.

back emf:
capacitive reactance:
Figure 23.52 An LC circuit is analogous to a mass oscillating on a spring with no friction and no driving force. Energy moves back and forth between
the inductor and capacitor, just as it moves from kinetic to potential in the mass-spring system.
PhET Explorations: Circuit Construction Kit (AC+DC), Virtual Lab
Build circuits with capacitors, inductors, resistors and AC or DC voltage sources, and inspect them using lab instruments
such as voltmeters and ammeters.
Figure 23.53 Circuit Construction Kit (AC+DC), Virtual Lab (http://cnx.org/content/m55420/1.2/circuit-construction-kit-ac-virtual-
lab_en.jar)
Glossary
the emf generated by a running motor, because it consists of a coil turning in a magnetic field; it opposes the
voltage powering the motor
the opposition of a capacitor to a change in current; calculated by XC = 1
2πfC

characteristic time constant:
eddy current:
electric generator:
electromagnetic induction:
emf induced in a generator coil:
energy stored in an inductor:
Faraday’s law of induction:
henry:
impedance:
inductance:
induction:
inductive reactance:
inductor:
Lenz’s law:
magnetic damping:
magnetic flux:
mutual inductance:
peak emf:
phase angle:
power factor:
resonant frequency:
self-inductance:
shock hazard:
step-down transformer:
step-up transformer:
thermal hazard:
three-wire system:
transformer:
denoted by τ , of a particular series RL circuit is calculated by τ = L
R
, where L is the
inductance and R is the resistance
a current loop in a conductor caused by motional emf
a device for converting mechanical work into electric energy; it induces an emf by rotating a coil in a
magnetic field
the process of inducing an emf (voltage) with a change in magnetic flux
emf = NABω sin ωt , where A is the area of an N -turn coil rotated at a constant
angular velocity ω in a uniform magnetic field B , over a period of time t
self-explanatory; calculated by Eind = 1
2
LI2
the means of calculating the emf in a coil due to changing magnetic flux, given by
emf = −N ΔΦ
Δt
the unit of inductance; 1 H = 1 Ω ⋅ s
the AC analogue to resistance in a DC circuit; it is the combined effect of resistance, inductive reactance, and
capacitive reactance in the form Z = R2
+ (XL − XC)2
a property of a device describing how efficient it is at inducing emf in another device
(magnetic induction) the creation of emfs and hence currents by magnetic fields
the opposition of an inductor to a change in current; calculated by XL = 2πfL
a device that exhibits significant self-inductance
the minus sign in Faraday’s law, signifying that the emf induced in a coil opposes the change in magnetic flux
the drag produced by eddy currents
the amount of magnetic field going through a particular area, calculated with Φ = BA cos θ where B is the
magnetic field strength over an area A at an angle θ with the perpendicular to the area
how effective a pair of devices are at inducing emfs in each other
emf0 = NABω
denoted by ϕ , the amount by which the voltage and current are out of phase with each other in a circuit
the amount by which the power delivered in the circuit is less than the theoretical maximum of the circuit due to
voltage and current being out of phase; calculated by cos ϕ
the frequency at which the impedance in a circuit is at a minimum, and also the frequency at which the
circuit would oscillate if not driven by a voltage source; calculated by f0 = 1
2π LC
how effective a device is at inducing emf in itself
the term for electrical hazards due to current passing through a human
a transformer that decreases voltage
a transformer that increases voltage
the term for electrical hazards due to overheating
the wiring system used at present for safety reasons, with live, neutral, and ground wires
a device that transforms voltages from one value to another using induction

transformer equation: the equation showing that the ratio of the secondary to primary voltages in a transformer equals the
ratio of the number of loops in their coils;
Vs
Vp
=
Ns
Np
Section Summary
• The crucial quantity in induction is magnetic flux Φ , defined to be Φ = BA cos θ , where B is the magnetic field strength
over an area A at an angle θ with the perpendicular to the area.
• Units of magnetic flux Φ are T ⋅ m2
.
• Any change in magnetic flux Φ induces an emf—the process is defined to be electromagnetic induction.
• Faraday’s law of induction states that the emfinduced by a change in magnetic flux is
emf = −NΔΦ
Δt
when flux changes by ΔΦ in a time Δt .
• If emf is induced in a coil, N is its number of turns.
• The minus sign means that the emf creates a current I and magnetic field B that oppose the change in flux ΔΦ —this
opposition is known as Lenz’s law.
23.3 Motional Emf
• An emf induced by motion relative to a magnetic field B is called a motional emf and is given by
emf = Bℓv (B, ℓ, and v perpendicular),
where ℓ is the length of the object moving at speed v relative to the field.
• Current loops induced in moving conductors are called eddy currents.
• They can create significant drag, called magnetic damping.
• An electric generator rotates a coil in a magnetic field, inducing an emfgiven as a function of time by
emf = NABω sin ωt,
where A is the area of an N -turn coil rotated at a constant angular velocity ω in a uniform magnetic field B .
• The peak emf emf0 of a generator is
emf0 = NABω.
23.6 Back Emf
• Any rotating coil will have an induced emf—in motors, this is called back emf, since it opposes the emf input to the motor.
23.7 Transformers
• Transformers use induction to transform voltages from one value to another.
• For a transformer, the voltages across the primary and secondary coils are related by
Vs
Vp
=
Ns
Np
,
where Vp and Vs are the voltages across primary and secondary coils having Np and Ns turns.
• The currents Ip and Is in the primary and secondary coils are related by
Is
Ip
=
Np
Ns
.
• A step-up transformer increases voltage and decreases current, whereas a step-down transformer decreases voltage and
increases current.
• Electrical safety systems and devices are employed to prevent thermal and shock hazards.

• Circuit breakers and fuses interrupt excessive currents to prevent thermal hazards.
• The three-wire system guards against thermal and shock hazards, utilizing live/hot, neutral, and earth/ground wires, and
grounding the neutral wire and case of the appliance.
• A ground fault interrupter (GFI) prevents shock by detecting the loss of current to unintentional paths.
• An isolation transformer insulates the device being powered from the original source, also to prevent shock.
• Many of these devices use induction to perform their basic function.
23.9 Inductance
• Inductance is the property of a device that tells how effectively it induces an emf in another device.
• Mutual inductance is the effect of two devices in inducing emfs in each other.
• A change in current ΔI1 / Δt in one induces an emf emf2 in the second:
emf2 = −M
ΔI1
Δt
,
where M is defined to be the mutual inductance between the two devices, and the minus sign is due to Lenz’s law.
• Symmetrically, a change in current ΔI2 / Δt through the second device induces an emf emf1 in the first:
emf1 = −M
ΔI2
Δt
,
where M is the same mutual inductance as in the reverse process.
• Current changes in a device induce an emf in the device itself.
• Self-inductance is the effect of the device inducing emf in itself.
• The device is called an inductor, and the emf induced in it by a change in current through it is
emf = −LΔI
Δt
,
where L is the self-inductance of the inductor, and ΔI / Δt is the rate of change of current through it. The minus sign
indicates that emf opposes the change in current, as required by Lenz’s law.
• The unit of self- and mutual inductance is the henry (H), where 1 H = 1 Ω ⋅ s .
• The self-inductance L of an inductor is proportional to how much flux changes with current. For an N -turn inductor,
L = NΔΦ
ΔI
.
• The self-inductance of a solenoid is
L =
µ0 N2
A
ℓ
(solenoid),
where N is its number of turns in the solenoid, A is its cross-sectional area, ℓ is its length, and
μ0 = 4π×10−7
T ⋅ m/A is the permeability of free space.
• The energy stored in an inductor Eind is
Eind = 1
2
LI2
.
23.10 RL Circuits
• When a series connection of a resistor and an inductor—an RL circuit—is connected to a voltage source, the time variation
of the current is
I = I0(1 − e−t / τ
) (turning on).
where I0 = V / R is the final current.
• The characteristic time constant τ is τ = L
R
, where L is the inductance and R is the resistance.
• In the first time constant τ , the current rises from zero to 0.632I0 , and 0.632 of the remainder in every subsequent time
interval τ .
• When the inductor is shorted through a resistor, current decreases as
I = I0e−t / τ
(turning off).
Here I0 is the initial current.
• Current falls to 0.368I0 in the first time interval τ , and 0.368 of the remainder toward zero in each subsequent time τ .

• For inductors in AC circuits, we find that when a sinusoidal voltage is applied to an inductor, the voltage leads the current
by one-fourth of a cycle, or by a 90º phase angle.
• The opposition of an inductor to a change in current is expressed as a type of AC resistance.
• Ohm’s law for an inductor is
I = V
XL
,
where V is the rms voltage across the inductor.
• XL is defined to be the inductive reactance, given by
XL = 2πfL,
with f the frequency of the AC voltage source in hertz.
• Inductive reactance XL has units of ohms and is greatest at high frequencies.
• For capacitors, we find that when a sinusoidal voltage is applied to a capacitor, the voltage follows the current by one-fourth
of a cycle, or by a 90º phase angle.
• Since a capacitor can stop current when fully charged, it limits current and offers another form of AC resistance; Ohm’s law
for a capacitor is
I = V
XC
,
where V is the rms voltage across the capacitor.
• XC is defined to be the capacitive reactance, given by
XC = 1
2πfC
.
• XC has units of ohms and is greatest at low frequencies.
• The AC analogy to resistance is impedance Z , the combined effect of resistors, inductors, and capacitors, defined by the
AC version of Ohm’s law:
I0 =
V0
Z
or Irms =
Vrms
Z
,
where I0 is the peak current and V0 is the peak source voltage.
• Impedance has units of ohms and is given by Z = R2
+ (XL − XC)2
.
• The resonant frequency f0 , at which XL = XC , is
f0 = 1
2π LC
.
• In an AC circuit, there is a phase angle ϕ between source voltage V and the current I , which can be found from
cos ϕ = R
Z
,
• ϕ = 0º for a purely resistive circuit or an RLC circuit at resonance.
• The average power delivered to an RLC circuit is affected by the phase angle and is given by
Pave = IrmsVrms cos ϕ,
cos ϕ is called the power factor, which ranges from 0 to 1.
Conceptual Questions
1. How do the multiple-loop coils and iron ring in the version of Faraday’s apparatus shown in Figure 23.3 enhance the
observation of induced emf?
2. When a magnet is thrust into a coil as in Figure 23.4(a), what is the direction of the force exerted by the coil on the magnet?
Draw a diagram showing the direction of the current induced in the coil and the magnetic field it produces, to justify your
response. How does the magnitude of the force depend on the resistance of the galvanometer?

3. Explain how magnetic flux can be zero when the magnetic field is not zero.
4. Is an emf induced in the coil in Figure 23.54 when it is stretched? If so, state why and give the direction of the induced
current.
Figure 23.54 A circular coil of wire is stretched in a magnetic field.
5. A person who works with large magnets sometimes places her head inside a strong field. She reports feeling dizzy as she
quickly turns her head. How might this be associated with induction?
6. A particle accelerator sends high-velocity charged particles down an evacuated pipe. Explain how a coil of wire wrapped
around the pipe could detect the passage of individual particles. Sketch a graph of the voltage output of the coil as a single
particle passes through it.
23.3 Motional Emf
7. Why must part of the circuit be moving relative to other parts, to have usable motional emf? Consider, for example, that the
rails in Figure 23.11 are stationary relative to the magnetic field, while the rod moves.
8. A powerful induction cannon can be made by placing a metal cylinder inside a solenoid coil. The cylinder is forcefully expelled
when solenoid current is turned on rapidly. Use Faraday’s and Lenz’s laws to explain how this works. Why might the cylinder get
live/hot when the cannon is fired?
9. An induction stove heats a pot with a coil carrying an alternating current located beneath the pot (and without a hot surface).
Can the stove surface be a conductor? Why won’t a coil carrying a direct current work?
10. Explain how you could thaw out a frozen water pipe by wrapping a coil carrying an alternating current around it. Does it
matter whether or not the pipe is a conductor? Explain.
11. Explain why magnetic damping might not be effective on an object made of several thin conducting layers separated by
insulation.
12. Explain how electromagnetic induction can be used to detect metals? This technique is particularly important in detecting
buried landmines for disposal, geophysical prospecting and at airports.
13. Using RHR-1, show that the emfs in the sides of the generator loop in Figure 23.23 are in the same sense and thus add.
14. The source of a generator’s electrical energy output is the work done to turn its coils. How is the work needed to turn the
generator related to Lenz’s law?
23.6 Back Emf
15. Suppose you find that the belt drive connecting a powerful motor to an air conditioning unit is broken and the motor is running
freely. Should you be worried that the motor is consuming a great deal of energy for no useful purpose? Explain why or why not.
23.7 Transformers
16. Explain what causes physical vibrations in transformers at twice the frequency of the AC power involved.
17. Does plastic insulation on live/hot wires prevent shock hazards, thermal hazards, or both?
18. Why are ordinary circuit breakers and fuses ineffective in preventing shocks?
19. A GFI may trip just because the live/hot and neutral wires connected to it are significantly different in length. Explain why.
23.9 Inductance
20. How would you place two identical flat coils in contact so that they had the greatest mutual inductance? The least?
21. How would you shape a given length of wire to give it the greatest self-inductance? The least?

22. Verify, as was concluded without proof in Example 23.7, that units of T ⋅ m2
/ A = Ω ⋅ s = H .
23. Presbycusis is a hearing loss due to age that progressively affects higher frequencies. A hearing aid amplifier is designed to
amplify all frequencies equally. To adjust its output for presbycusis, would you put a capacitor in series or parallel with the hearing
aid’s speaker? Explain.
24. Would you use a large inductance or a large capacitance in series with a system to filter out low frequencies, such as the 100
Hz hum in a sound system? Explain.
25. High-frequency noise in AC power can damage computers. Does the plug-in unit designed to prevent this damage use a
large inductance or a large capacitance (in series with the computer) to filter out such high frequencies? Explain.
26. Does inductance depend on current, frequency, or both? What about inductive reactance?
27. Explain why the capacitor in Figure 23.55(a) acts as a low-frequency filter between the two circuits, whereas that in Figure
23.55(b) acts as a high-frequency filter.
Figure 23.55 Capacitors and inductors. Capacitor with high frequency and low frequency.
28. If the capacitors in Figure 23.55 are replaced by inductors, which acts as a low-frequency filter and which as a high-
frequency filter?
29. Does the resonant frequency of an AC circuit depend on the peak voltage of the AC source? Explain why or why not.
30. Suppose you have a motor with a power factor significantly less than 1. Explain why it would be better to improve the power
factor as a method of improving the motor’s output, rather than to increase the voltage input.

Problems & Exercises
1. What is the value of the magnetic flux at coil 2 in Figure
23.56 due to coil 1?
Figure 23.56 (a) The planes of the two coils are perpendicular. (b) The
wire is perpendicular to the plane of the coil.
2. What is the value of the magnetic flux through the coil in
Figure 23.56(b) due to the wire?
3. Referring to Figure 23.57(a), what is the direction of the
current induced in coil 2: (a) If the current in coil 1 increases?
(b) If the current in coil 1 decreases? (c) If the current in coil 1
is constant? Explicitly show how you follow the steps in the
Problem-Solving Strategy for Lenz's Law.
Figure 23.57 (a) The coils lie in the same plane. (b) The wire is in the
plane of the coil
4. Referring to Figure 23.57(b), what is the direction of the
current induced in the coil: (a) If the current in the wire
increases? (b) If the current in the wire decreases? (c) If the
current in the wire suddenly changes direction? Explicitly
show how you follow the steps in the Problem-Solving
Strategy for Lenz’s Law.
5. Referring to Figure 23.58, what are the directions of the
currents in coils 1, 2, and 3 (assume that the coils are lying in
the plane of the circuit): (a) When the switch is first closed?
(b) When the switch has been closed for a long time? (c) Just
after the switch is opened?
Figure 23.58
6. Repeat the previous problem with the battery reversed.
7. Verify that the units of ΔΦ / Δt are volts. That is, show
that 1 T ⋅ m2
/ s = 1 V .
8. Suppose a 50-turn coil lies in the plane of the page in a
uniform magnetic field that is directed into the page. The coil
originally has an area of 0.250 m2
. It is stretched to have no
area in 0.100 s. What is the direction and magnitude of the
induced emf if the uniform magnetic field has a strength of
1.50 T?
9. (a) An MRI technician moves his hand from a region of
very low magnetic field strength into an MRI scanner’s 2.00 T
field with his fingers pointing in the direction of the field. Find
the average emf induced in his wedding ring, given its
diameter is 2.20 cm and assuming it takes 0.250 s to move it
into the field. (b) Discuss whether this current would
significantly change the temperature of the ring.
Referring to the situation in the previous problem: (a) What
current is induced in the ring if its resistance is 0.0100 Ω ?
(b) What average power is dissipated? (c) What magnetic
field is induced at the center of the ring? (d) What is the
direction of the induced magnetic field relative to the MRI’s
field?
11. An emf is induced by rotating a 1000-turn, 20.0 cm
diameter coil in the Earth’s 5.00×10−5
T magnetic field.
What average emf is induced, given the plane of the coil is
originally perpendicular to the Earth’s field and is rotated to be
parallel to the field in 10.0 ms?
12. A 0.250 m radius, 500-turn coil is rotated one-fourth of a
revolution in 4.17 ms, originally having its plane perpendicular
to a uniform magnetic field. (This is 60 rev/s.) Find the
magnetic field strength needed to induce an average emf of
10,000 V.
Approximately how does the emf induced in the loop in
Figure 23.57(b) depend on the distance of the center of the
loop from the wire?
(a) A lightning bolt produces a rapidly varying magnetic field.
If the bolt strikes the earth vertically and acts like a current in
a long straight wire, it will induce a voltage in a loop aligned
like that in Figure 23.57(b). What voltage is induced in a 1.00
m diameter loop 50.0 m from a 2.00×106
A lightning strike,

if the current falls to zero in 25.0 μs ? (b) Discuss
circumstances under which such a voltage would produce
noticeable consequences.
23.3 Motional Emf
15. Use Faraday’s law, Lenz’s law, and RHR-1 to show that
the magnetic force on the current in the moving rod in Figure
23.11 is in the opposite direction of its velocity.
16. If a current flows in the Satellite Tether shown in Figure
23.12, use Faraday’s law, Lenz’s law, and RHR-1 to show that
there is a magnetic force on the tether in the direction
opposite to its velocity.
17. (a) A jet airplane with a 75.0 m wingspan is flying at 280
m/s. What emf is induced between wing tips if the vertical
component of the Earth’s field is 3.00×10−5
T ? (b) Is an
emf of this magnitude likely to have any consequences?
Explain.
18. (a) A nonferrous screwdriver is being used in a 2.00 T
magnetic field. What maximum emf can be induced along its
12.0 cm length when it moves at 6.00 m/s? (b) Is it likely that
this emf will have any consequences or even be noticed?
19. At what speed must the sliding rod in Figure 23.11 move
to produce an emf of 1.00 V in a 1.50 T field, given the rod’s
length is 30.0 cm?
20. The 12.0 cm long rod in Figure 23.11 moves at 4.00 m/s.
What is the strength of the magnetic field if a 95.0 V emf is
induced?
21. Prove that when B , ℓ , and v are not mutually
perpendicular, motional emf is given by emf = Bℓvsin θ . If
v is perpendicular to B , then θ is the angle between ℓ
and B . If ℓ is perpendicular to B , then θ is the angle
between v and B .
22. In the August 1992 space shuttle flight, only 250 m of the
conducting tether considered in Example 23.2 could be let
out. A 40.0 V motional emf was generated in the Earth’s
5.00×10−5
T field, while moving at 7.80×103
m/s . What
was the angle between the shuttle’s velocity and the Earth’s
field, assuming the conductor was perpendicular to the field?
Derive an expression for the current in a system like that in
Figure 23.11, under the following conditions. The resistance
between the rails is R , the rails and the moving rod are
identical in cross section A and have the same resistivity ρ .
The distance between the rails is l, and the rod moves at
constant speed v perpendicular to the uniform field B . At
time zero, the moving rod is next to the resistance R .
The Tethered Satellite in Figure 23.12 has a mass of 525 kg
and is at the end of a 20.0 km long, 2.50 mm diameter cable
with the tensile strength of steel. (a) How much does the
cable stretch if a 100 N force is exerted to pull the satellite in?
(Assume the satellite and shuttle are at the same altitude
above the Earth.) (b) What is the effective force constant of
the cable? (c) How much energy is stored in it when stretched
by the 100 N force?
The Tethered Satellite discussed in this module is producing
5.00 kV, and a current of 10.0 A flows. (a) What magnetic
drag force does this produce if the system is moving at 7.80
km/s? (b) How much kinetic energy is removed from the
system in 1.00 h, neglecting any change in altitude or velocity
during that time? (c) What is the change in velocity if the
mass of the system is 100,000 kg? (d) Discuss the long term
consequences (say, a week-long mission) on the space
shuttle’s orbit, noting what effect a decrease in velocity has
and assessing the magnitude of the effect.
26. Make a drawing similar to Figure 23.14, but with the
pendulum moving in the opposite direction. Then use
Faraday’s law, Lenz’s law, and RHR-1 to show that magnetic
force opposes motion.
27.
Figure 23.59 A coil is moved into and out of a region of uniform
magnetic field. A coil is moved through a magnetic field as
shown in Figure 23.59. The field is uniform inside the
rectangle and zero outside. What is the direction of the
induced current and what is the direction of the magnetic
force on the coil at each position shown?
28. Calculate the peak voltage of a generator that rotates its
200-turn, 0.100 m diameter coil at 3600 rpm in a 0.800 T
field.
29. At what angular velocity in rpm will the peak voltage of a
generator be 480 V, if its 500-turn, 8.00 cm diameter coil
rotates in a 0.250 T field?
30. What is the peak emf generated by rotating a 1000-turn,
20.0 cm diameter coil in the Earth’s 5.00×10−5
T magnetic
field, given the plane of the coil is originally perpendicular to
the Earth’s field and is rotated to be parallel to the field in 10.0
ms?
31. What is the peak emf generated by a 0.250 m radius,
500-turn coil is rotated one-fourth of a revolution in 4.17 ms,
originally having its plane perpendicular to a uniform magnetic
field. (This is 60 rev/s.)
32. (a) A bicycle generator rotates at 1875 rad/s, producing
an 18.0 V peak emf. It has a 1.00 by 3.00 cm rectangular coil
in a 0.640 T field. How many turns are in the coil? (b) Is this
number of turns of wire practical for a 1.00 by 3.00 cm coil?
This problem refers to the bicycle generator considered in the
previous problem. It is driven by a 1.60 cm diameter wheel
that rolls on the outside rim of the bicycle tire. (a) What is the
velocity of the bicycle if the generator’s angular velocity is
1875 rad/s? (b) What is the maximum emf of the generator
when the bicycle moves at 10.0 m/s, noting that it was 18.0 V
under the original conditions? (c) If the sophisticated
generator can vary its own magnetic field, what field strength
will it need at 5.00 m/s to produce a 9.00 V maximum emf?
34. (a) A car generator turns at 400 rpm when the engine is
idling. Its 300-turn, 5.00 by 8.00 cm rectangular coil rotates in
an adjustable magnetic field so that it can produce sufficient

voltage even at low rpms. What is the field strength needed to
produce a 24.0 V peak emf? (b) Discuss how this required
field strength compares to those available in permanent and
electromagnets.
35. Show that if a coil rotates at an angular velocity ω , the
period of its AC output is 2π/ω .
36. A 75-turn, 10.0 cm diameter coil rotates at an angular
velocity of 8.00 rad/s in a 1.25 T field, starting with the plane
of the coil parallel to the field. (a) What is the peak emf? (b) At
what time is the peak emf first reached? (c) At what time is
the emf first at its most negative? (d) What is the period of the
AC voltage output?
37. (a) If the emf of a coil rotating in a magnetic field is zero at
t = 0 , and increases to its first peak at t = 0.100 ms , what
is the angular velocity of the coil? (b) At what time will its next
maximum occur? (c) What is the period of the output? (d)
When is the output first one-fourth of its maximum? (e) When
is it next one-fourth of its maximum?
A 500-turn coil with a 0.250 m2
area is spun in the Earth’s
5.00×10−5
T field, producing a 12.0 kV maximum emf. (a)
At what angular velocity must the coil be spun? (b) What is
23.6 Back Emf
39. Suppose a motor connected to a 120 V source draws
10.0 A when it first starts. (a) What is its resistance? (b) What
current does it draw at its normal operating speed when it
develops a 100 V back emf?
40. A motor operating on 240 V electricity has a 180 V back
emf at operating speed and draws a 12.0 A current. (a) What
is its resistance? (b) What current does it draw when it is first
started?
41. What is the back emf of a 120 V motor that draws 8.00 A
at its normal speed and 20.0 A when first starting?
42. The motor in a toy car operates on 6.00 V, developing a
4.50 V back emf at normal speed. If it draws 3.00 A at normal
speed, what current does it draw when starting?
The motor in a toy car is powered by four batteries in series,
which produce a total emf of 6.00 V. The motor draws 3.00 A
and develops a 4.50 V back emf at normal speed. Each
battery has a 0.100 Ω internal resistance. What is the
resistance of the motor?
23.7 Transformers
44. A plug-in transformer, like that in Figure 23.29, supplies
9.00 V to a video game system. (a) How many turns are in its
secondary coil, if its input voltage is 120 V and the primary
coil has 400 turns? (b) What is its input current when its
output is 1.30 A?
45. An American traveler in New Zealand carries a
transformer to convert New Zealand’s standard 240 V to 120
V so that she can use some small appliances on her trip. (a)
What is the ratio of turns in the primary and secondary coils of
her transformer? (b) What is the ratio of input to output
current? (c) How could a New Zealander traveling in the
United States use this same transformer to power her 240 V
appliances from 120 V?
46. A cassette recorder uses a plug-in transformer to convert
120 V to 12.0 V, with a maximum current output of 200 mA.
(a) What is the current input? (b) What is the power input? (c)
Is this amount of power reasonable for a small appliance?
47. (a) What is the voltage output of a transformer used for
rechargeable flashlight batteries, if its primary has 500 turns,
its secondary 4 turns, and the input voltage is 120 V? (b)
What input current is required to produce a 4.00 A output? (c)
What is the power input?
48. (a) The plug-in transformer for a laptop computer puts out
7.50 V and can supply a maximum current of 2.00 A. What is
the maximum input current if the input voltage is 240 V?
Assume 100% efficiency. (b) If the actual efficiency is less
than 100%, would the input current need to be greater or
smaller? Explain.
49. A multipurpose transformer has a secondary coil with
several points at which a voltage can be extracted, giving
outputs of 5.60, 12.0, and 480 V. (a) The input voltage is 240
V to a primary coil of 280 turns. What are the numbers of
turns in the parts of the secondary used to produce the output
voltages? (b) If the maximum input current is 5.00 A, what are
the maximum output currents (each used alone)?
50. A large power plant generates electricity at 12.0 kV. Its old
transformer once converted the voltage to 335 kV. The
secondary of this transformer is being replaced so that its
output can be 750 kV for more efficient cross-country
transmission on upgraded transmission lines. (a) What is the
ratio of turns in the new secondary compared with the old
secondary? (b) What is the ratio of new current output to old
output (at 335 kV) for the same power? (c) If the upgraded
transmission lines have the same resistance, what is the ratio
of new line power loss to old?
51. If the power output in the previous problem is 1000 MW
and line resistance is 2.00 Ω , what were the old and new
line losses?
The 335 kV AC electricity from a power transmission line is
fed into the primary coil of a transformer. The ratio of the
number of turns in the secondary to the number in the primary
is Ns / Np = 1000 . (a) What voltage is induced in the
secondary? (b) What is unreasonable about this result? (c)
Which assumption or premise is responsible?
Consider a double transformer to be used to create very large
voltages. The device consists of two stages. The first is a
transformer that produces a much larger output voltage than
its input. The output of the first transformer is used as input to
a second transformer that further increases the voltage.
Construct a problem in which you calculate the output voltage
of the final stage based on the input voltage of the first stage
and the number of turns or loops in both parts of both
transformers (four coils in all). Also calculate the maximum
output current of the final stage based on the input current.
Discuss the possibility of power losses in the devices and the
effect on the output current and power.
A short circuit to the grounded metal case of an appliance
occurs as shown in Figure 23.60. The person touching the
case is wet and only has a 3.00 kΩ resistance to earth/
ground. (a) What is the voltage on the case if 5.00 mA flows

through the person? (b) What is the current in the short circuit
if the resistance of the earth/ground wire is 0.200 Ω ? (c)
Will this trigger the 20.0 A circuit breaker supplying the
appliance?
Figure 23.60 A person can be shocked even when the case of an
appliance is grounded. The large short circuit current produces a voltage
on the case of the appliance, since the resistance of the earth/ground
wire is not zero.
23.9 Inductance
55. Two coils are placed close together in a physics lab to
demonstrate Faraday’s law of induction. A current of 5.00 A in
one is switched off in 1.00 ms, inducing a 9.00 V emf in the
other. What is their mutual inductance?
56. If two coils placed next to one another have a mutual
inductance of 5.00 mH, what voltage is induced in one when
the 2.00 A current in the other is switched off in 30.0 ms?
57. The 4.00 A current through a 7.50 mH inductor is
switched off in 8.33 ms. What is the emf induced opposing
this?
58. A device is turned on and 3.00 A flows through it 0.100
ms later. What is the self-inductance of the device if an
induced 150 V emf opposes this?
59. Starting with emf2 = −M
ΔI1
Δt
, show that the units of
inductance are (V ⋅ s)/A = Ω ⋅ s .
60. Camera flashes charge a capacitor to high voltage by
switching the current through an inductor on and off rapidly. In
what time must the 0.100 A current through a 2.00 mH
inductor be switched on or off to induce a 500 V emf?
61. A large research solenoid has a self-inductance of 25.0 H.
(a) What induced emf opposes shutting it off when 100 A of
current through it is switched off in 80.0 ms? (b) How much
energy is stored in the inductor at full current? (c) At what rate
in watts must energy be dissipated to switch the current off in
80.0 ms? (d) In view of the answer to the last part, is it
surprising that shutting it down this quickly is difficult?
62. (a) Calculate the self-inductance of a 50.0 cm long, 10.0
cm diameter solenoid having 1000 loops. (b) How much
energy is stored in this inductor when 20.0 A of current flows
through it? (c) How fast can it be turned off if the induced emf
cannot exceed 3.00 V?
63. A precision laboratory resistor is made of a coil of wire
1.50 cm in diameter and 4.00 cm long, and it has 500 turns.
(a) What is its self-inductance? (b) What average emf is
induced if the 12.0 A current through it is turned on in 5.00 ms
(one-fourth of a cycle for 50 Hz AC)? (c) What is its
inductance if it is shortened to half its length and counter-
wound (two layers of 250 turns in opposite directions)?
64. The heating coils in a hair dryer are 0.800 cm in diameter,
have a combined length of 1.00 m, and a total of 400 turns.
(a) What is their total self-inductance assuming they act like a
single solenoid? (b) How much energy is stored in them when
6.00 A flows? (c) What average emf opposes shutting them
off if this is done in 5.00 ms (one-fourth of a cycle for 50 Hz
AC)?
65. When the 20.0 A current through an inductor is turned off
in 1.50 ms, an 800 V emf is induced, opposing the change.
What is the value of the self-inductance?
66. How fast can the 150 A current through a 0.250 H
inductor be shut off if the induced emf cannot exceed 75.0
V?
A very large, superconducting solenoid such as one used in
MRI scans, stores 1.00 MJ of energy in its magnetic field
when 100 A flows. (a) Find its self-inductance. (b) If the coils
“go normal,” they gain resistance and start to dissipate
thermal energy. What temperature increase is produced if all
the stored energy goes into heating the 1000 kg magnet,
given its average specific heat is 200 J/kg·ºC ?
A 25.0 H inductor has 100 A of current turned off in 1.00 ms.
(a) What voltage is induced to oppose this? (b) What is
23.10 RL Circuits
69. If you want a characteristic RL time constant of 1.00 s,
and you have a 500 Ω resistor, what value of self-
inductance is needed?
70. Your RL circuit has a characteristic time constant of 20.0
ns, and a resistance of 5.00 MΩ . (a) What is the inductance
of the circuit? (b) What resistance would give you a 1.00 ns
time constant, perhaps needed for quick response in an
oscilloscope?
71. A large superconducting magnet, used for magnetic
resonance imaging, has a 50.0 H inductance. If you want
current through it to be adjustable with a 1.00 s characteristic
time constant, what is the minimum resistance of system?
72. Verify that after a time of 10.0 ms, the current for the
situation considered in Example 23.9 will be 0.183 A as
stated.
73. Suppose you have a supply of inductors ranging from
1.00 nH to 10.0 H, and resistors ranging from 0.100 Ω to
1.00 MΩ . What is the range of characteristic RL time
constants you can produce by connecting a single resistor to
a single inductor?
74. (a) What is the characteristic time constant of a 25.0 mH
inductor that has a resistance of 4.00 Ω ? (b) If it is
connected to a 12.0 V battery, what is the current after 12.5
ms?

75. What percentage of the final current I0 flows through an
inductor L in series with a resistor R , three time constants
after the circuit is completed?
76. The 5.00 A current through a 1.50 H inductor is dissipated
by a 2.00 Ω resistor in a circuit like that in Figure 23.44 with
the switch in position 2. (a) What is the initial energy in the
inductor? (b) How long will it take the current to decline to
5.00% of its initial value? (c) Calculate the average power
dissipated, and compare it with the initial power dissipated by
the resistor.
77. (a) Use the exact exponential treatment to find how much
time is required to bring the current through an 80.0 mH
inductor in series with a 15.0 Ω resistor to 99.0% of its final
value, starting from zero. (b) Compare your answer to the
approximate treatment using integral numbers of τ . (c)
Discuss how significant the difference is.
78. (a) Using the exact exponential treatment, find the time
required for the current through a 2.00 H inductor in series
with a 0.500 Ω resistor to be reduced to 0.100% of its
original value. (b) Compare your answer to the approximate
treatment using integral numbers of τ . (c) Discuss how
significant the difference is.
79. At what frequency will a 30.0 mH inductor have a
reactance of 100 Ω ?
80. What value of inductance should be used if a 20.0 kΩ
reactance is needed at a frequency of 500 Hz?
81. What capacitance should be used to produce a
2.00 MΩ reactance at 60.0 Hz?
82. At what frequency will an 80.0 mF capacitor have a
reactance of 0.250 Ω ?
83. (a) Find the current through a 0.500 H inductor connected
to a 60.0 Hz, 480 V AC source. (b) What would the current be
at 100 kHz?
84. (a) What current flows when a 60.0 Hz, 480 V AC source
is connected to a 0.250 μF capacitor? (b) What would the
current be at 25.0 kHz?
85. A 20.0 kHz, 16.0 V source connected to an inductor
produces a 2.00 A current. What is the inductance?
86. A 20.0 Hz, 16.0 V source produces a 2.00 mA current
when connected to a capacitor. What is the capacitance?
87. (a) An inductor designed to filter high-frequency noise
from power supplied to a personal computer is placed in
series with the computer. What minimum inductance should it
have to produce a 2.00 kΩ reactance for 15.0 kHz noise?
(b) What is its reactance at 60.0 Hz?
88. The capacitor in Figure 23.55(a) is designed to filter low-
frequency signals, impeding their transmission between
circuits. (a) What capacitance is needed to produce a
100 kΩ reactance at a frequency of 120 Hz? (b) What
would its reactance be at 1.00 MHz? (c) Discuss the
implications of your answers to (a) and (b).
89. The capacitor in Figure 23.55(b) will filter high-frequency
signals by shorting them to earth/ground. (a) What
capacitance is needed to produce a reactance of 10.0 mΩ
for a 5.00 kHz signal? (b) What would its reactance be at 3.00
Hz? (c) Discuss the implications of your answers to (a) and
(b).
In a recording of voltages due to brain activity (an EEG), a
10.0 mV signal with a 0.500 Hz frequency is applied to a
capacitor, producing a current of 100 mA. Resistance is
negligible. (a) What is the capacitance? (b) What is
Consider the use of an inductor in series with a computer
operating on 60 Hz electricity. Construct a problem in which
you calculate the relative reduction in voltage of incoming
high frequency noise compared to 60 Hz voltage. Among the
things to consider are the acceptable series reactance of the
inductor for 60 Hz power and the likely frequencies of noise
coming through the power lines.
92. An RL circuit consists of a 40.0 Ω resistor and a 3.00
mH inductor. (a) Find its impedance Z at 60.0 Hz and 10.0
kHz. (b) Compare these values of Z with those found in
Example 23.12 in which there was also a capacitor.
93. An RC circuit consists of a 40.0 Ω resistor and a
5.00 μF capacitor. (a) Find its impedance at 60.0 Hz and
10.0 kHz. (b) Compare these values of Z with those found in
Example 23.12, in which there was also an inductor.
94. An LC circuit consists of a 3.00 mH inductor and a
5.00 µF capacitor. (a) Find its impedance at 60.0 Hz and
10.0 kHz. (b) Compare these values of Z with those found in
Example 23.12 in which there was also a resistor.
95. What is the resonant frequency of a 0.500 mH inductor
connected to a 40.0 μF capacitor?
96. To receive AM radio, you want an RLC circuit that can be
made to resonate at any frequency between 500 and 1650
kHz. This is accomplished with a fixed 1.00 μH inductor
connected to a variable capacitor. What range of capacitance
is needed?
97. Suppose you have a supply of inductors ranging from
1.00 nH to 10.0 H, and capacitors ranging from 1.00 pF to
0.100 F. What is the range of resonant frequencies that can
be achieved from combinations of a single inductor and a
single capacitor?
98. What capacitance do you need to produce a resonant
frequency of 1.00 GHz, when using an 8.00 nH inductor?
99. What inductance do you need to produce a resonant
frequency of 60.0 Hz, when using a 2.00 μF capacitor?
100. The lowest frequency in the FM radio band is 88.0 MHz.
(a) What inductance is needed to produce this resonant
frequency if it is connected to a 2.50 pF capacitor? (b) The
capacitor is variable, to allow the resonant frequency to be
adjusted to as high as 108 MHz. What must the capacitance
be at this frequency?
101. An RLC series circuit has a 2.50 Ω resistor, a 100 μH
inductor, and an 80.0 μF capacitor.(a) Find the circuit’s
impedance at 120 Hz. (b) Find the circuit’s impedance at 5.00

kHz. (c) If the voltage source has Vrms = 5.60 V , what is
Irms at each frequency? (d) What is the resonant frequency
of the circuit? (e) What is Irms at resonance?
102. An RLC series circuit has a 1.00 kΩ resistor, a
150 μH inductor, and a 25.0 nF capacitor. (a) Find the
circuit’s impedance at 500 Hz. (b) Find the circuit’s
impedance at 7.50 kHz. (c) If the voltage source has
Vrms = 408 V , what is Irms at each frequency? (d) What
is the resonant frequency of the circuit? (e) What is Irms at
resonance?
103. An RLC series circuit has a 2.50 Ω resistor, a 100 μH
inductor, and an 80.0 μF capacitor. (a) Find the power factor
at f = 120 Hz . (b) What is the phase angle at 120 Hz? (c)
What is the average power at 120 Hz? (d) Find the average
power at the circuit’s resonant frequency.
104. An RLC series circuit has a 1.00 kΩ resistor, a
150 μH inductor, and a 25.0 nF capacitor. (a) Find the
power factor at f = 7.50 Hz . (b) What is the phase angle at
this frequency? (c) What is the average power at this
frequency? (d) Find the average power at the circuit’s
resonant frequency.
105. An RLC series circuit has a 200 Ω resistor and a 25.0
mH inductor. At 8000 Hz, the phase angle is 45.0º . (a) What
is the impedance? (b) Find the circuit’s capacitance. (c) If
Vrms = 408 V is applied, what is the average power
supplied?
106. Referring to Example 23.14, find the average power at
10.0 kHz.
Test Prep for AP® Courses
1. To produce current with a coil and bar magnet you can:
a. move the coil but not the magnet.
b. move the magnet but not the coil.
c. move either the coil or the magnet.
d. It is not possible to produce current.
2. Calculate the magnetic flux for a coil of area 0.2 m2
placed
at an angle of θ=60º (as shown in the figure above) to a
magnetic field of strength 1.5×10-3
T. At what angle will the
flux be at its maximum?
3. The emf induced in a coil that is rotating in a magnetic field
will be at a maximum when
a. the magnetic flux is at a maximum.
b. the magnetic flux is at a minimum.
c. the change in magnetic flux is at a maximum.
d. the change in magnetic flux is at a minimum.
4. A coil with circular cross section and 20 turns is rotating at
a rate of 400 rpm between the poles of a magnet. If the
magnetic field strength is 0.6 T and peak voltage is 0.2 V,
what is the radius of the coil? If the emf of the coil is zero at t
= 0 s, when will it reach its peak emf?
23.7 Transformers
5. Which of the following statements is true for a step-down
transformer? Select two answers.
a. Primary voltage is higher than secondary voltage.
b. Primary voltage is lower than secondary voltage.
c. Primary current is higher than secondary current.
d. Primary current is lower than secondary current.
6. An ideal step-up transformer with turn ratio 1:30 is supplied
with an input power of 120 W. If the output voltage is 210 V,
calculate the output power and input current.
7. Which of the following statements is true for an isolation
transformer?
a. It has more primary turns than secondary turns.
b. It has fewer primary turns than secondary turns.
c. It has an equal number of primary and secondary turns.
d. It can have more, fewer, or an equal number of primary
and secondary turns.
8. Explain the working of a ground fault interrupter (GFI).

Ap2 unit5 open stax notes

More Related Content

What's hot

Viewers also liked

Similar to Ap2 unit5 open stax notes

More from Sarah Sue Calbio

Recently uploaded

Ap2 unit5 open stax notes