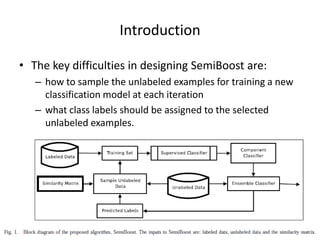
SemiBoost is a boosting algorithm for semi-supervised learning that utilizes both labeled and unlabeled data. It works by iteratively selecting the most confidently labeled unlabeled examples based on pairwise similarities, assigning labels, and training a classifier. The algorithm aims to minimize inconsistencies between labeled examples and unlabeled example labels implied by similarities. It formulates the problem as optimizing an objective function balancing these inconsistencies. Experimental results show SemiBoost improves classification accuracy over other semi-supervised and supervised methods on benchmark datasets.

1. SemiBoost : Boosting for Semi-supervised LearningPavan Kumar Mallapragada, Student Member, IEEE, Rong Jin, Member, IEEE,Anil K. Jain, Fellow, IEEE, and Yi Liu, Student Member, IEEEPresented by Yueng-Tien ,LoReference:SemiBoost: Boosting for Semi-supervised Learning P. K. Mallapragada, R. Jin, A. K. Jain, and Y. Liu, IEEE Transaction on Pattern Analysis and Machine Intelligence(PAMI), 31(11):2000-2014, 2009

2. outlineIntroductionRelated WorkSemi-Supervised BoostingResults and DiscussionConclusions and Future WorkGaussian Fields and Harmonic Functions

3. IntroductionThe key idea of semi-supervised learning, specifically semi-supervised classification, is to exploit both labeled and unlabeled data to learn a classification model.There is an immense need for algorithms that can utilize the small amount of labeled data, combined with the large amount of unlabeled data to build efficient classification systems.

4. IntroductionExisting semi-supervised classification algorithms may be classified into two categories based on their underlying assumptions.manifold assumption cluster assumption

5. Introductionmanifold assumption : the data lie on a low dimensional manifold in the input spacecluster assumption : the data samples with high similarity between them must share the same label.

6. IntroductionMost semi-supervised learning approaches design specialized learning algorithms to effectively utilize both labeled and unlabeled data.We refer to this problem of improving the performance of any supervised learning algorithm using unlabeled data as Semi-supervise Improvement, to distinguish our work from the standard semi-supervised learning problems.

7. IntroductionThe key difficulties in designing SemiBoost are: how to sample the unlabeled examples for training a new classification model at each iteration what class labels should be assigned to the selected unlabeled examples.

8. IntroductionOne way to address the above questions is to exploit both the clustering assumption and the large margin criterionSelecting the unlabeled examples with the highest classification confidence and assign them the class labels that are predicted by the current classifier.A problem with this strategy is that the introduction of examples with predicted class labels may only help to increase the classification margin, without actually providing any novel information to the classifier.

9. IntroductionTo overcome the above problem, we propose using the pairwise similarity measurements to guide the selection of unlabeled examples at each iteration, as well as for assigning class labels to them.

10. Related Work

11. Related WorkAn inductive algorithm can be used to predict the labels of samples that are unseen during training (irrespective of it being labeled or unlabeled).Transductivealgorithms are limited to predicting only the labels of the unlabeled samples seen during training.

12. Related WorkA popular way to define the inconsistency between the labels of the samples and the pairwise similarities Sij is the quadratic criterion: where L is the combinatorial graph Laplacian.The task is to assign values to the unknown labels in such a way that the overall inconsistency is minimized.

13. Semi-Supervised Improvementdenote the entire data set, including both the labeled and the unlabeled examples.the first nl examples are labeled, given by the imputed class labels of unlabeled examplesLet denote the symmetric similarity matrix, where represents the similarity between xi and xj. denote the submatrix of the similarity matrix denote the submatrix of the similarity matrix‘A’ denote the given supervised learning algorithm

14. Semi-Supervised ImprovementThe goal of semi-supervised improvement is to improve the performance of A iteratively by treating A like a black box, using the unlabeled examples and the pairwise similarity S.In the semi-supervised improvement problem, we aim to build an ensemble classifier which utilizes the unlabeled samples in the way a graph-based approach would utilize.

15. An outline of the SemiBoost algorithm for semi-supervised improvementStart with an empty ensemble.At each iteration,Compute the peusdo label (and its confidence)for each unlabeled example (using existing ensemble, and the pairwise similarity).Sample most confident pseudo labeled examples;combine them with the labeled samples and train a component classifier using the supervised learning algorithm A.Update the ensemble by including the componentclassifier with an appropriate weight.

16. SemiBoostThe unlabeled samples must be assigned labels following two main criteria: The points with high similarity among unlabeled samples must share the same label Those unlabeled samples which are highly similar to a labeled sample must share its label.Our objective function is a combination of two terms: one measuring the inconsistency between labeled and unlabeled examples and the other measuring the inconsistency among the unlabeled examples

17. SemiBoostInspired by the harmonic function approach, we define , the inconsistency between class labels y and the similarity measurement S, asNote that (1) can be expanded as and due to the symmetry of S

18. SemiBoostWe have where is the hyperbolic cosine function.Rewriting (1) using the function reveals the connection between the quadratic penalty used in the graph-Laplacian-based approaches, and the exponential penalty used in the current approach

19. SemiBoostUsing a penalty not only facilitates the derivation of boosting-based algorithms but also increases the classification margin.The inconsistency between labeled and unlabeled examples is defined as

20. SemiBoostCombining (1) and (3) leads to the objective function,The constant C is introduced to weight the importance between the labeled and the unlabeled data. Given the objective function in (4), the optimal class label yu is found by minimizing F.

21. SemiBoostThe problem can now be formally expressed asThe following procedure is adopted to derive the boosting algorithm:The labels for the unlabeled samples yiuare replaced by the ensemble predictions over the corresponding data sample.A bound-optimization-based approach is then used to find the ensemble classifier minimizing the objective function.The bounds are simplified further to obtain the sampling scheme, and other required parameters.

22. The SemiBoost algorithmCompute the pairwise similarity Si,j between any two examples.Initialize H(x) = 0For t = 1, 2, . . . , TCompute pi and qi for every example using Equations (9)and(10)Compute the class label zi= sign(pi − qi) for each exampleSample example xi by the weight |pi − qi|Apply the algorithm A to train a binary classifier ht(x) using the sampled examples and their class labels ziCompute αt using Equation (11)Update the classification function as H(x) ← H(x) + αtht(x)

23. SemiBoost-AlgorithmLet denote the two-class classifi-cation model that is learned at the t-th iteration by the algorithm A. Let denote the combined classification model learned after the first T iterations. where is the combination weight.

24. SemiBoost-AlgorithmThis leads to the following optimization problem:

25. This expression involves products of variables and making it nonlinear and, hence , difficult to optimize.Appendix

26. SemiBoost-Algorithm (prop.1)Minimizing (7) is equivalent to minimizing the function where and

27. Appendix

28. SemiBoost-Algorithm (prop.2)The expression in (8) is difficult to optimize since the weight and the classifier h(x) are coupled together.Minimizing (8) is equivalent to minimizingWe denote the upper bound in the above equation by F2.

29. SemiBoost-Algorithm (prop.3)To minimize F2, the optimal class label zi for the example xi is zi= sign(pi – qi) and the weight for sampling example xi is |pi-qi|. The optimal that minimizes F1 is

30. SemiBoost-AlgorithmAt each relaxation, the “touch-point” is maintained between the objective function and the upper bound. As a result, the procedure guarantees: The objective function always decreases through iterationsThe final solution converges to a local minimum.

31. The SemiBoost algorithmCompute the pairwise similarity Si,j between any two examples.Initialize H(x) = 0For t = 1, 2, . . . , TCompute pi and qi for every example using Equations (9)and(10)Compute the class label zi= sign(pi − qi) for each exampleSample example xi by the weight |pi − qi|Apply the algorithm A to train a binary classifier ht(x) using the sampled examples and their class labels ziCompute αt using Equation (11)Update the classification function as H(x) ← H(x) + αtht(x)

32. SemiBoost-AlgorithmLet be the weighted error made by the classifier, whereAs in the case of AdaBoost, can be expressed as which is very similar to the weighting factor of AdaBoost, differing only by a constant factor of 1/2 .

33. SemiBoost-AlgorithmTheorem 1. Let be the combination weights that are computed by running the SemiBoost algorithm (Fig. 1). Then, the objective function at the et t 1Tst iteration, i.e., Ftt1, is bounded as follows:where

34. Results and Discussion

35. X. Zhu, Z. Ghahramani, and J. Lafferty, “Semi-supervised learning using gaussian fields and harmonic functions,” in Proc. 20t International Conference on Machine Learning, pp. 912–919, 2003