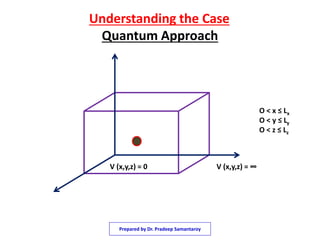
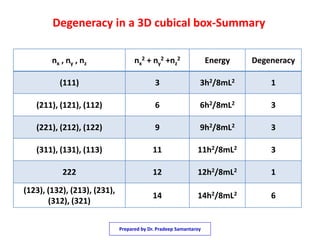
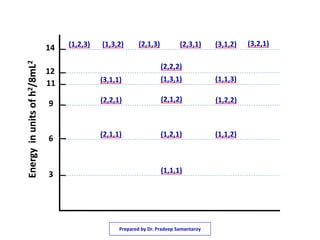
1) The document discusses solving the Schrodinger equation for an electron confined to a three dimensional box. 2) It shows that using separation of variables, the Schrodinger equation can be broken into three one dimensional equations that are each equivalent to the particle in a one dimensional box. 3) The solutions for the wavefunctions and energy levels are presented, with the energy levels increasing with higher quantum numbers and becoming degenerate with multiple combinations of the quantum numbers.

1. Dr. Pradeep Samantaroy
Department of Chemistry
Rayagada Autonomous College, Rayagada
pksroy82@gmail.com; pksroy82@yahoo.in
9444078968

2. V (x,y,z) = 0 V (x,y,z) = ∞
O < x ≤ Lx
O < y ≤ Ly
O < z ≤ Lz
Understanding the Case
Quantum Approach
Prepared by Dr. Pradeep Samantaroy

3. Let’s solve the case…!
)()()(
)()()(
2 2
2
2
2
2
22
rErrV
dz
rd
dy
rd
dx
rd
m










The Schrodinger’s equation for the electron in three dimensional
box can be represented as
)()()()(
2
2
2
rErrVr
m
 

It can also be represented as
Prepared by Dr. Pradeep Samantaroy

4. Outside and on the Edges of Box
Applying boundary conditions outside the box
 Er
m


*)(
2
2
2

0
2

Hence, the probability of finding electron outside the 3D box is zero.
Boundary conditions
ψ(0,y,z) = ψ(Lx,y,z) = 0
Ψ(x,0,z) = Ψ(x,Ly,z) = 0
ψ(x,y,0) = ψ(x,y,Lz) = 0
Prepared by Dr. Pradeep Samantaroy

5. Inside the box
)(
)()()(
2 2
2
2
2
2
22
rE
dz
rd
dy
rd
dx
rd
m









 0)( rVSince
To solve this equation, separation of variable can be applied.
ψ(x,y,z)= X(x) Y(y) Z(z)
Now we can see that each function has its own variable:
X(x) is a function for variable x only
Y(y) is a function of variable y only
Z(z) is a function of variable z only
Prepared by Dr. Pradeep Samantaroy

6. Now substituting the value of Ψ (x,y,z) in the Schrodinger’s equation and then
dividing the whole by xyz,
E
dz
zZd
zZdy
yYd
yYdx
xXd
xXm








2
2
2
2
2
22
)(
)(
1)(
)(
1)(
)(
1
2

Now the final equation can be represented as
Prepared by Dr. Pradeep Samantaroy

7. We also partition the total energy into its rightful components:
E = Ex​ + Ey​ + Ez​
Now each component can be separated as
Does this equation looks similar to what we have studied already!!!
It is the case of particle in 1D box. Hence the solution of x component is
)(
2
)(2
2
2
xXE
dx
xXd
m
x
 
x
x
x
x
L
xn
L

 sin
2

Prepared by Dr. Pradeep Samantaroy

8. )(
2
)(2
2
2
yYE
dy
yYd
m
y
 
y
y
y
y
L
yn
L

 sin
2

Similarly the y and z component can be represented as
)(
2
)(2
2
2
zZE
dz
zZd
m
z
 
z
z
z
z
L
zn
L

 sin
2

Prepared by Dr. Pradeep Samantaroy

9. Therefore the final solution for a particle in 3D box can be represented as

























z
z
zy
y
yx
x
x L
zn
LL
yn
LL
xn
L
r

 sin
2
sin
2
sin
2
)(





















z
z
y
y
x
x
zyx L
zn
L
yn
L
xn
LLL
r

 sinsinsin
8
)(





















z
z
y
y
x
x
L
zn
L
yn
L
xn
V
r

 sinsinsin
8
)(
or
or
Prepared by Dr. Pradeep Samantaroy

10. Energy
2
22
8 x
x
x
mL
hn
E 
Now the energy of the x component can be written as
Similarly the energy of the y and z component can be written.
Now the total energy can be written as
2
22
2
22
2
22
888 z
z
y
y
x
x
zyx
mL
hn
mL
hn
mL
hn
EEEE 








 2
2
2
2
2
22
8 z
z
y
y
x
x
L
n
L
n
L
n
m
h
E
Prepared by Dr. Pradeep Samantaroy

11. If the 3D box is a cube?
If the 3D box is a cube then Lx = Ly = Lz = L

























L
zn
L
yn
L
xn
V
r zyx 
 sinsinsin
8
)(








 2
2
2
2
2
22
8 L
n
L
n
L
n
m
h
E zyx
 222
2
2
8
zyx nnn
mL
h
E 
Prepared by Dr. Pradeep Samantaroy

12. Degeneracy in a 3D cubical box
Can any one or all of nx, ny, nz values be zero??
Ground state energy can be calculated using
nx= 1, ny= 1, nz= 1
  2
2
222
2
2
111
8
3
111
8 mL
h
mL
h
E 
Zero Point Energy
Prepared by Dr. Pradeep Samantaroy

13. Degeneracy in a 3D cubical box
For the first excitation state energy can be calculated using following
combination of quantum numbers
(nx,ny, nz) = (2,1,1) or (1,2,1) or (1,1,2)
2
2
112121211
8
6
mL
h
EEE 
Corresponding to these combinations of (nx, ny, nz), three different wave
functions and three different states are possible. Hence, the first excited state
is said to be three-fold or triply degenerate.
Prepared by Dr. Pradeep Samantaroy

14. nx , ny , nz nx
2 + ny
2 +nz
2 Energy Degeneracy
(111) 3 3h2/8mL2 1
(211), (121), (112) 6 6h2/8mL2 3
(221), (212), (122) 9 9h2/8mL2 3
(311), (131), (113) 11 11h2/8mL2 3
222 12 12h2/8mL2 1
(123), (132), (213), (231),
(312), (321)
14 14h2/8mL2 6
Degeneracy in a 3D cubical box-Summary
Prepared by Dr. Pradeep Samantaroy

15. 12
9
6
3
14
11
(1,1,1)
(1,2,1)(2,1,1) (1,1,2)
(2,1,2)(2,2,1) (1,2,2)
(1,3,1)(3,1,1) (1,1,3)
(2,2,2)
(1,3,2)(1,2,3) (2,1,3) (3,1,2)(2,3,1) (3,2,1)
Energyinunitsofh2/8mL2
Prepared by Dr. Pradeep Samantaroy